Scroll to:
Dynamics of a Flat Rigid Body on a Horizontal Plane
https://doi.org/10.23947/2687-1653-2025-25-1-7-13
EDN: ATOYXO
Abstract
Introduction. The study of the motion of a rigid body carrying moving masses greatly simplifies the design of capsule robots that can move inside aggressive environments and perform the required operations. The following cases have been studied quite well: movement during interaction of a solid body with a reference plane and in aggressive environments; vibratory displacement of bulk media and solids on a vibrating base; optimization of rigid body motion; variation of average speed and acceleration at different intervals of motion; dependence of average speed on task parameters; control of the motion speed of the internal mass for the fastest possible rotation of a rigid body. However, at present, insufficient attention has been paid in the literature to the problems of studying the motion of a heavy flat body along a horizontal plane under the action of a harmonic force directed at an angle to the horizon, specifically, in terms of taking into account all possible driving modes and their features. This does not allow determining the optimal parameters of the problem. Therefore, the objective of this research was to identify the features of all possible modes of motion of a heavy solid body along a horizontal plane under the action of a harmonic force directed at an angle to the horizon.
Materials and Methods. The equations of motion of the mechanical system were used. Both analytical approaches and numerical methods were used to solve the steady-state equations of motion of the system. The dry friction model was adopted as a friction model, which made it possible to obtain accurate solutions for positive and negative values of the slip velocity up to constants. Values of these constants were determined from the docking conditions and the periodicity of the solution.
Results. An analytical solution to the problem for periodic solutions was obtained. Three possible motion modes were identified. Using numerical analysis, the dependences of the average speed of a body motion over the period on the angle of inclination of the force to the horizon were constructed. The optimal direction of force was established.
Discussion and Conclusion. The results of the conducted research allowed us to determine the optimal values of the problem parameters in order to reach the required value of the average velocity of a solid body. In particular, optimal values of the amplitude of the force and its direction can be found to reach the maximum value of the average velocity of motion of a solid.
Keywords
For citations:
Munitsyn A.I., Tsoy V.E. Dynamics of a Flat Rigid Body on a Horizontal Plane. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):7-13. https://doi.org/10.23947/2687-1653-2025-25-1-7-13. EDN: ATOYXO
Introduction. Recently, the tasks of designing the movement of robots carrying the required objects, including those moving in aggressive environments [1] and capable of performing the requested operations [2], have become increasingly urgent. As a rule, the model that takes into account the interaction of a solid body with a reference plane is the dry friction model [3]. This task has a lot in common with the task of vibratory movement of bulk media and solids on a vibrating base [4]. Optimization of the capsule robot motion with varying average speed was considered in [5]. In [6], acceleration was varied at different motion intervals. A capsule robot, the control of which was based on these two principles, was studied in [7]. In [8], optimization of average speed was presented. In [9], a mathematical model of the electromagnetic force of core retraction was constructed. The dependence of average speed on excitation parameters was studied in [10]. In [11], the law of control of the speed of the internal mass for the fastest turn of the robot was investigated. The motion of a capsule robot with two masses moving along parallel guides was considered in [12], and along two mutually perpendicular guides — in [13]. Robots with linearly moving masses and a rotor were described in [14]. In all the listed papers, the motion of a rigid body along a horizontal plane under the action of a harmonic force directed at an angle to the horizon was not studied, and various motion modes and their features were not established. Therefore, this research was aimed at identifying the features of all possible modes of motion of a rigid body along a horizontal plane under the action of a harmonic force directed at an angle to the horizon. Achieving this objective allows us to determine the optimal parameters of the research problem, such as: the optimal angle of action of the force to build up maximum speed, the necessary and optimal values of the parameters of the research problem to build up the required speed of motion of a rigid body.
Materials and Methods. To solve the problem, we compose an equation of motion for a mechanical system. The solution to the equation for each mode of motion can be obtained separately.
Equations of Motion. A body has mass m and moves along the horizontal plane along the x-axis. The body is subjected to harmonic force F = A0 cos(qt), directed at angle b to the horizontal plane, where A0 — amplitude of the acting external force; q — frequency of the acting external force. Let Vx be the speed of the body in the horizontal direction; Vy — speed of the body in the vertical direction.
The motion of a rigid body is described by a system of two equations:
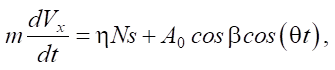
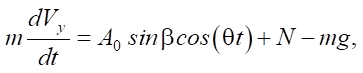
where g — gravitational acceleration; N — reaction force of the base. In the equations given, the friction force is taken into account using the Coulomb model. For this purpose, the coefficient of dry friction h and dimensionless parameter s are introduced, which at rest can take any value in the range from –1 to 1. In the case of slippage, when Vx is not equal to zero, the friction force is constant and directed opposite to the slip velocity. The dimensionless parameter is given by expression s = –sign(Vx).
Next, we assume that the reaction forces of the base are distributed uniformly over the reference surface, and the body moves without separation from the base, i.e., the body speed in the vertical direction is zero. Of the two equations for describing the motion of a rigid body, one remains — for movement in the horizontal direction:
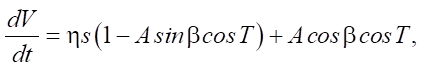 (1)
(1)
where T = qt — nondimensional time; V = Vxq/g — dimensionless speed and dimensionless amplitude of vibration excitation A = A0/(mg).
A similar problem of the motion of a rigid body carrying an unbalanced rotor along an inclined plane was considered in [15].
Equation (1) has a trivial solution at V(t)=0. This means that the body is at rest during the time interval under consideration. Then, the friction force parameter changes according to the following law:
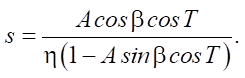 (2)
(2)
At this, the amplitude value of the projection of the external force onto the horizontal axis is not enough to start the body movement.
Motion with two instantaneous stops. The solution to equation (1) in the case of slippage between the body and the base:
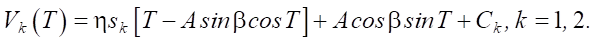 (3)
(3)
Here, the following notations are introduced: V1 — for the positive velocity of the body, to which s1 = –1 corresponds; V2 — for the negative velocity; s2 = 1. From here on, we will consider stationary solutions to the equation of motion of the body. We introduce the following notations for the motion of the body with a positive velocity: j11 denotes the start time of the motion, and j12 — the end time of the motion of the body, through j21 and j22 — the same values for motion with negative velocity. For six unknowns, we obtain four equations:
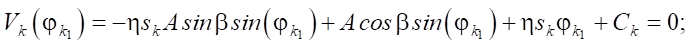 (4)
(4)
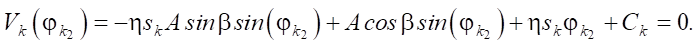 (5)
(5)
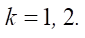
From the condition of absence of a long stop of the body, we obtain two more conditions:
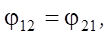 (6)
(6)
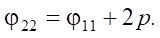 (7)
(7)
The integration constants C1 and C2 can be eliminated from equations (4) and (5). From the obtained equations, phases j11, j12, j21 and j22 are found numerically. The resulting transcendental equations have two solutions each. To select the correct solution, we determine the second derivative of the velocity:
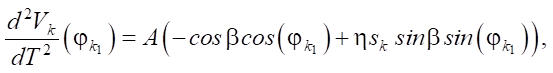 (8)
(8)
which should be positive at k = 1 and negative at k = 2.
Motion with two long stops. In this case, conditions (6) and (7) are not valid. When moving from rest to motion, the acceleration of the body must be zero:
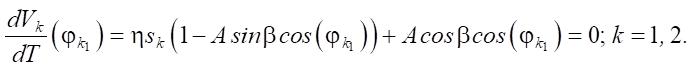 (9)
(9)
From equation (9), we obtain an exact solution for the phases of motion:
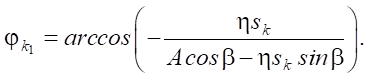 (10)
(10)
The required root is determined similarly to the previous case. Constant Ck and phase jk2 are found from (4) and (5). If the condition A > η / (cos β + η sin β) is true, the body can move with a speed greater than zero; and provided that the amplitude of the excitation of oscillations is A > η / (cos β + η sin β), the body moves with a speed less than zero.
If the end time of the body motion with positive velocity j12 is less than the start time of the body motion with negative velocity j21, and j21 is less than j11 + 2p, then the motion of the rigid body can have two long stops.
Let us consider the motion of a body with instantaneous and prolonged stops. The reaction of the horizontal base, as well as the force acting on the body, changes according to a harmonic law, periodic solutions are possible here.
In the case of a rigid body moving with a positive velocity and an instantaneous transition to negative, and from negative to positive, after a long stop, we obtain a system of equations (4), (5) for k = 1, 2 (9), for k = 1 and condition j12=j21. Phase j11 is determined by expression (10). For the remaining unknowns, an exact solution is also determined. The obtained solution is valid when the condition j22< j11+2p is met.
In the instantaneous transition from negative to positive velocity of a rigid body, and from positive to negative, after a long stop, the system of equations (4–5) for k = 1, 2 remains unchanged. We compose equation (9) for k = 2, and replace the instantaneous stop condition with j22 = j11 + 2p.
Thus, for all possible modes of stationary motion of a rigid body, four phases and two integration constants are determined. On one period of motion, using formulas (3), it is possible to construct the dependence of the average velocity of motion of rigid body vm on the angle of inclination of the line of action of the external force b. On the interval j11 < t < j12, the rigid body moves with a velocity greater than zero, and when j21 < t < j22, the rigid body moves with a velocity less than zero. On the interval j12 < t < j21 and j22 < t < j11 + 2p, the rigid body does not move. When j12 and j21 or j22 and j11 + 2p coincide, the velocity of the body at these points changes instantly.
The constructed solution for three types of motion and a state of rest (2) for one period of oscillations allows us to determine the average speed of motion of a rigid body:
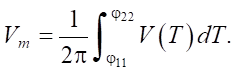
Research Results. The results of the study were obtained with dry friction coefficient h = 0.1 and excitation amplitude A = 0.6. The dependences of the four phases jkj(b), (ji k = 1, 2) on the angle of inclination of the external force to the horizon are shown in Figure 1. The dotted curves indicate the points of instantaneous change in the speed of the body, and the solid curves indicate the points of change in speed with a long stop.
At small angles of inclination of force j12=j21, j22 = j11 + 2p, the motion of the rigid body occurs with two instantaneous stops. The motion pattern changes when angle b increases. At point B1, the curve branches j22(b) = j11(b) + 2p. As a result, we have two curves: j22(b) and j11(b), and at point В2, the curve j12(b) = j21(b) branches into j12(b) and j21(b). Between points В1 and В2, the rigid body may have a long and instantaneous stop. Between points В2 and В3, the motion may have two long stops. At point B3, curves j22(b) and j21(b) merge. Between points B3 and B4, during the motion of the rigid body within one period at a speed greater than zero, there may be one long stop. At large values of the angle of inclination, the body is at rest.
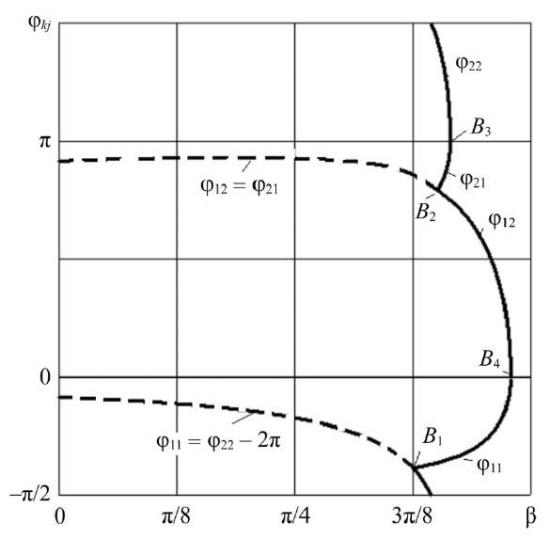
Fig. 1. Dependences of phases of stationary motion on the angle of inclination of the applied force
Figure 2 shows the dependences of the average velocity of solid body vm on the angle of inclination of the line of action of the external force b for friction coefficient 0.1 and several excitation amplitudes. For any values of the excitation amplitude and horizontal action of the force (b = 0), the average velocity of the solid body is zero. With an increase in b, the average velocity grows up. The points of change of the motion modes are indicated only on the curve A = 0.6. For each value of the force amplitude, there is an optimal angle at which the average velocity of motion is maximum.
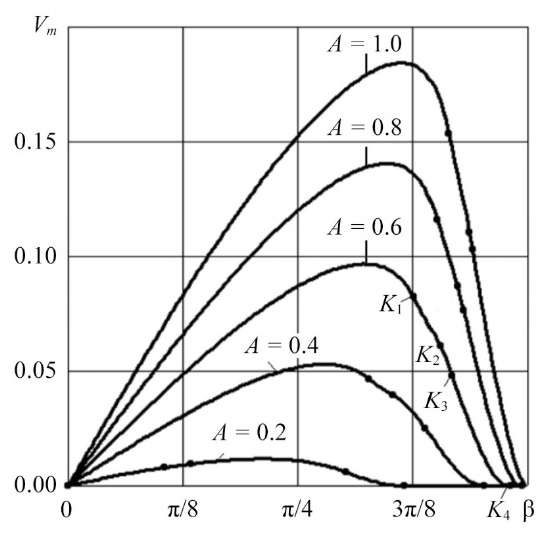
Fig. 2. Dependence of average speed V m on angle b
Discussion and Conclusion. The motion of a rigid body along a horizontal plane under the action of a harmonic force directed at an angle to the horizon is studied. The analytical and numerical results show that for all possible modes of stationary motion of a rigid body, four phases are determined. The obtained dependences of the phases of stationary motion and the average speed of motion of a rigid body on the angle of inclination of the line of action of an external force allow us to determine the necessary and optimal values of the parameters of the problem to achieve the required speed of motion of a rigid body. It is shown that for each value of the amplitude of the force, there is an optimal angle at which the average speed of motion is maximum.
The results obtained can be used in the development of algorithms and design of the movement of robotic devices when moving along a horizontal plane, taking into account the action of harmonic loads.
References
1. Chernousko FL. Plane Motions by Rigid Body Controlled by means of Movable Mass. Doklady RAN: Physics. 2020;494(1):69–74.
2. Chernousko FL. Optimal Motion Control of a Two–Mass System. Doklady AN. 2018;480(5):528–532. (In Russ.)
3. Andronov VV, Zhuravlev VF. Dry Friction in Problems of Mechanics. Monograph. Moscow–Izhevsk: Publ. House “IKI”; 2010. 184 p. (In Russ.)
4. Blekhman II. Vibrational Mechanics and Vibrational Rheology (Theory and Applications). Moscow: Fizmatlit; 2018. 751 p. (In Russ.)
5. Chernousko FL. On the Motion of a Body Containing a Movable Internal Mass. Doklady AN. 2005;405(1):56–60. (In Russ.)
6. Chernous’ko FL. Analysis and Optimization of the Motion of a Body Controlled by means of a Movable Internal Mass. Journal of Applied Mathematics and Mechanics. 2006;70(6):819–842. https://doi.org/10.1016/j.jappmathmech.2007.01.003
7. Hongyi Li, Katsuhisa Furuta, Felix L Chernousko. Motion Generation of the Capsubot Using Internal Force and Static Friction. In: Proc. 45th IEEE Conference on Decision and Control. New York City: IEEE; 2006. P. 6575–6580. https://doi.org/10.1109/CDC.2006.377472
8. Nunuparov AM, Sukhanov AN, Syrykh NV. Optimization of the Average Speed of a Capsule Robot by Nonlinear Model-Proactive Control. In: Proc. XXXIII International Innovative Conference of Young Scientists and Students on Problems of Machine Science. Moscow: IMASH RAN; 2021. P. 436–441. (In Russ.)
9. Syrykh NV, Nunuparov AM, Sukhanov AN. On Building a Mathematical Model of the Electromagnetic Force of a Solenoid for a Capsule Robot. In: Proc. XXXIII International Innovative Conference of Young Scientists and Students on Problems of Machine Science. Moscow: IMASH RAN; 2021. P. 484–490. (In Russ.)
10. Bolotnik NN, Nunuparov AM, Chashchukhin VG. Capsule-Type Vibration-Driven Robot with an Electromagnetic Actuator and an Opposing Spring: Dynamics and Control of Motion. Journal of Computer and Systems Sciences International. 2016;(6):146–160.
11. Shmatkov AM. Periodic Solutions to the Optimal Control Problem of Rotation of a Rigid Body Using Internal Mass. Moscow University Bulletin. Mathematics. Mechanics. 2020;(3):63–67. URL: https://www.mathnet.ru/links/3f7d22880247a4d39922b11f27ea3c8c/vmumm4333.pdf (accessed: 18.11.2024).
12. Sakharov AV. Rotation of a Body with Two Movable Internal Masses on a Rough Plane. Journal of Applied Mathematics and Mechanics. 2015;79(2):132–141. URL: https://pmm.ipmnet.ru/ru/Issues.php?y=2015&n=2&p=196 (accessed: 18.11.2024).
13. Xiong Zhang, Jian Xu, Hongbin Fang. A Vibration-Driven Planar Locomotion Robot – Shell. Robotica. 2018;36(9):1402–1420. http://doi.org/10.1017/S0263574718000383
14. Chernousko FL. Movement of a Body along a Plane under the Influence of Moving Internal Masses. Doklady AN. 2016;470(4):406–410. (In Russ.)
15. Munitsyn AI, Krainova LN. Vibratory Motion of a Rigid Body along an Inclined Plane. Engineering and Automation Problems. 2023;(1):31–35.
About the Authors
A. I. MunitsynRussian Federation
Alexander I. Munitsyn, Dr.Sci. (Eng.), Professor of the Robotics, Mechatronics, Dynamics and Strength of Machines Department
14, Krasnokazarmennaia Str., Moscow, 111250
V. E. Tsoy
Russian Federation
Valeryan E. Tsoy, Cand.Sci. (Phys.-Math.), Associate Professor of the Robotics, Mechatronics, Dynamics and Strength of Machines Department
14, Krasnokazarmennaia Str., Moscow, 111250
Review
For citations:
Munitsyn A.I., Tsoy V.E. Dynamics of a Flat Rigid Body on a Horizontal Plane. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):7-13. https://doi.org/10.23947/2687-1653-2025-25-1-7-13. EDN: ATOYXO












































