Перейти к:
Динамика плоского твердого тела на горизонтальной плоскости
https://doi.org/10.23947/2687-1653-2025-25-1-7-13
EDN: ATOYXO
Аннотация
Введение. Исследование движения твердого тела, несущего подвижные массы, значительно упрощает проектирование капсульных роботов, которые могут перемещаться внутри агрессивных сред и выполнять необходимые операции. Достаточно хорошо изучены случаи: движения при взаимодействии твердого тела с опорной плоскостью и в агрессивных средах; вибрационного перемещения сыпучих сред и твердых тел на вибрирующем основании; оптимизации движения твердых тел; варьирования средней скорости и ускорения на различных интервалах движения; зависимости средней скорости от параметров задачи; управления скоростью перемещения внутренней массы для наискорейшего поворота твердого тела. Однако в настоящее время в литературе уделено недостаточно внимания задачам исследования движения тяжелого плоского тела по горизонтальной плоскости под действием гармонической силы, направленной под углом к горизонту, особенно в плане учета всех возможных режимов движения и их особенностей. Это не позволяет определять оптимальные параметры задачи. Поэтому целью данной работы стало выявление особенностей всех возможных режимов движения тяжелого твердого тела по горизонтальной плоскости под действием гармонической силы, направленной под углом к горизонту.
Материалы и методы. В работе использовали уравнения движения механической системы. Для решения стационарных уравнений движения системы применялись как аналитические подходы, так и численные методы. В качестве модели трения была принята модель сухого трения, что позволило получить точные решения для положительного и отрицательного значения скорости проскальзывания с точностью до констант. Значения этих констант определялись из условий стыковки и периодичности решения.
Результаты исследования. Получено аналитическое решение задачи для периодических решений. Выявлены три возможных режима движения. С помощью численного анализа построены зависимости средней за период скорости движения тела от угла наклона силы к горизонту. Установлено оптимальное направление силы.
Обсуждение и заключение. Результаты проведенных исследований позволяют определить оптимальные значения параметров задачи для достижения необходимого значения средней скорости движения твердого тела. В частности, могут быть найдены оптимальные значения амплитуды силы и ее направления для достижения максимального значения средней скорости движения твердого тела.
Ключевые слова
Для цитирования:
Муницын А.И., Цой В.Э. Динамика плоского твердого тела на горизонтальной плоскости. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):7-13. https://doi.org/10.23947/2687-1653-2025-25-1-7-13. EDN: ATOYXO
For citation:
Munitsyn A.I., Tsoy V.E. Dynamics of a Flat Rigid Body on a Horizontal Plane. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):7-13. https://doi.org/10.23947/2687-1653-2025-25-1-7-13. EDN: ATOYXO
Введение. В последнее время все большую актуальность имеют задачи проектирования движения роботов, несущих необходимые объекты, в том числе, перемещаемые в агрессивных средах [1] и способные выполнять требуемые операции [2]. Как правило, модель, учитывающая взаимодействие твердого тела с опорной плоскостью, это модель сухого трения [3]. В этой задаче много общего с задачей вибрационного перемещения сыпучих сред и твердых тел на вибрирующем основании [4]. Оптимизация движения капсульного робота при варьировании средней скорости рассматривалась в [5]. В [6] изменялось ускорение на различных интервалах движения. Капсульный робот, управление которым основано на этих двух принципах, рассмотрен в [7]. В работе [8] приведена оптимизация средней скорости. В [9] построена математическая модель электромагнитной силы втягивания сердечника. Зависимость средней скорости движения от параметров возбуждения рассмотрена в [10]. В [11] исследуется закон управления скоростью движения внутренней массы для наискорейшего поворота робота. Движение капсульного робота с двумя массами, движущимися по параллельным направляющим, рассмотрено в [12], а по двум взаимно перпендикулярным направляющим — в [13]. Роботы с линейно движущимися массами и ротором рассмотрены в [14]. Во всех перечисленных работах не исследовалось движение твердого тела по горизонтальной плоскости под действием гармонической силы, направленной под углом к горизонту, не устанавливались различные режимы движения и их особенности. Поэтому целью данного исследования являлось выявление особенностей всех возможных режимов движения твердого тела по горизонтальной плоскости под действием гармонической силы, направленной под углом к горизонту. Достижение поставленной цели позволяет определить оптимальные параметры задачи исследования, например, такие как: оптимальный угол действия силы для достижения максимальной скорости, необходимые и оптимальные значения параметров задачи исследования для достижения требуемой скорости движения твердого тела.
Материалы и методы. Для решения поставленной задачи составляем уравнение движения механической системы. Решение уравнения для каждого режима движения может быть получено отдельно.
Уравнения движения. Тело имеет массу m и двигается по горизонтальной плоскости вдоль оси x. На тело действует гармоническая сила F = A0 cos(qt), направленная под углом b к горизонтальной плоскости, где A0 — амплитуда действующей внешней силы; q — частота действующей внешней силы. Обозначим Vx — скорость тела в горизонтальном направлении; Vy — скорость тела в вертикальном направлении.
Движение твердого тела описывается системой двух уравнений:
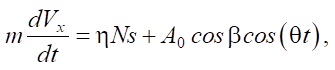
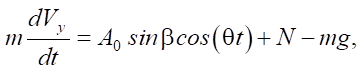
где g — ускорение свободного падения; N — сила реакции основания. В приведенных уравнениях сила трения учитывается по модели Кулона. Для этого введен коэффициент сухого трения h и безразмерный параметр s, который в состоянии покоя может принимать любое значение в диапазоне от –1 до 1. В случае проскальзывания, при Vx не равной нулю, сила трения постоянна и направлена противоположно скорости проскальзывания. Безразмерный параметр задается выражением s = –sign(Vx).
Далее полагаем, что силы реакции основания распределены равномерно по опорной поверхности и движение тела происходит без отрыва от основания, то есть скорость тела в вертикальном направлении равна нулю. Из двух уравнений для описания движения твердого тела остается одно — для движения в горизонтальном направлении:
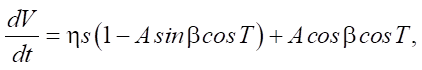 (1)
(1)
где T = qt — безразмерное время; V = Vxq/g — безразмерная скорость и безразмерная амплитуда возбуждения колебаний A = A0/(mg).
Похожая задача о движении твердого тела, несущего несбалансированный ротор по наклонной плоскости, была рассмотрена в [15].
Уравнение (1) имеет тривиальное решение при V(t) = 0. Это означает то, что тело находится в покое на рассматриваемом промежутке времени. Тогда параметр силы трения меняется по следующему закону:
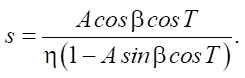 (2)
(2)
Тогда амплитудного значения проекции внешней силы на горизонтальную ось недостаточно для начала движения тела.
Движение с двумя мгновенными остановками. Решение уравнения (1) в случае проскальзывания между телом и основанием:
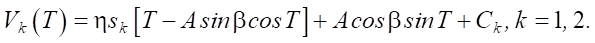 (3)
(3)
Здесь введены следующие обозначения: V1 — для положительной скорости тела, которой соответствует s1 = –1; V2 — для отрицательной скорости; s2 = 1. Здесь и далее будем рассматривать стационарные решения уравнения движения тела. Введем следующие обозначения для движения тела с положительной скоростью: j11 обозначим время начала движения, а j12 — время окончания движения тела. Через j21 и j22 — те же значения для движения с отрицательной скоростью. Для шести неизвестных получаем четыре уравнения:
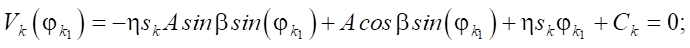 (4)
(4)
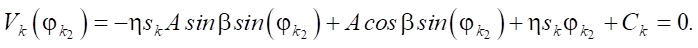 (5)
(5)
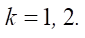
Из условия отсутствия длительной остановки тела получаем еще два условия:
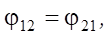 (6)
(6)
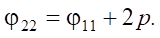 (7)
(7)
Константы интегрирования C1 и C2 могут быть исключены из уравнений (4) и (5). Из полученных уравнений численно находятся фазы j11, j12, j21 и j22. Полученные трансцендентные уравнения имеют по два решения. Для выбора правильного решения определяем вторую производную скорости:
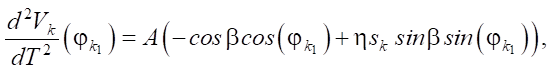 (8)
(8)
которая должна быть положительна при k = 1 и отрицательна при k = 2.
Движение с двумя длительными остановками. В этом случае условия (6) и (7) несправедливы. При переходе от состояния покоя к движению ускорение тела должно быть равно нулю:
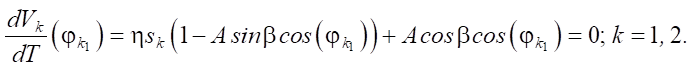 (9)
(9)
Из уравнения (9) получаем точное решение для фаз движения:
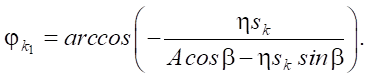 (10)
(10)
Нужный корень определяется аналогично предыдущему случаю. Константа Ck и фаза jk2 находятся из (4) и (5). Если справедливо условие A > η / (cos β + η sin β), тело может двигаться со скоростью больше нуля, а при условии, что амплитуда возбуждения колебаний — A > η / (cos β + η sin β), движение тела происходит со скоростью меньше нуля.
Если время окончания движения тела с положительной скоростью j12 меньше времени начала движения тела с отрицательной скоростью j21, а j21 меньше, чем j11 + 2p, то движение твердого тела может иметь две продолжительные остановки.
Рассмотрим движение тела с мгновенной и продолжительной остановками. Реакция горизонтального основания, как и действующая на тело сила, меняется по гармоническому закону, здесь возможны периодические решения.
В случае движения твердого тела с положительной скоростью и мгновенного перехода к отрицательной, а от отрицательной к положительной, после продолжительной остановки получаем систему уравнений (4), (5) для k = 1, 2, (9) для k = 1 и условия j12 = j21. Фаза j11 определяется выражением (10). Для остальных неизвестных также определяется точное решение. Полученное решение справедливо при выполнении условия j22 < j11 + 2p.
При мгновенном переходе от отрицательной скорости движения твердого тела к положительной, а от положительной к отрицательной, после длительной остановки, система уравнений (4–5) при k = 1, 2, остается без изменений. Уравнение (9) составляем для k = 2, а условие мгновенной остановки заменяем на j22 = j11 + 2p.
Таким образом, для всех возможных режимов стационарного движения твердого тела определяются четыре фазы и две константы интегрирования. На одном периоде движения, используя формулы (3), можно построить зависимость средней скорости движения твердого тела vm от угла наклона линии действия внешней силы b. На интервале j11 < t < j12 движение твердого тела происходит со скоростью больше нуля, а при j21 < t < j22 движение твердого тела происходит со скоростью меньше нуля. На интервале j12 < t < j21 и j22 < t< j11 + 2p твердое тело не двигается. При совпадении j12 и j21 или j22 и j11 + 2p скорость тела в этих точках меняется мгновенно.
Построенное решение для трех типов движения и состояния покоя (2) за один период колебаний позволяет определить среднюю скорость движения твердого тела:
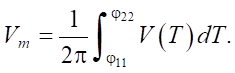
Результаты исследования. Результаты исследования получены при коэффициенте сухого трения h = 0,1 и амплитуде возбуждения A = 0,6. Зависимости четырех фаз jkj(b), (j,k=1,2) от угла наклона внешней силы к горизонту представлены на рис. 1. Пунктирными кривыми обозначены точки мгновенного изменения скорости движения тела, сплошными кривыми — точки изменения скорости с продолжительной остановкой.
При малых углах наклона силы j12 = j21, j22 = j11 + 2p движение твердого тела происходит при двух моментальных остановках. Характер движения меняется при изменении угла b в большую сторону. В точке B1 кривая разветвляется j22(b) = j11(b) + 2p. В результате имеем две кривые: j22(b) и j11(b), а в точке В2 разветвляется кривая j12(b) = j21(b) на j12(b) и j21(b). Между точками В1 и В2 твердое тело может иметь продолжительную и мгновенную остановки. Между точками В2 и В3 движение может иметь две продолжительные остановки. В точке B3 кривые j22(b) и j21(b) сливаются. Между точками B3 и B4 при движения твердого тела в пределах одного периода при скорости большей нуля может быть одна длительная остановка. При больших значениях угла наклона тело находится в покое.
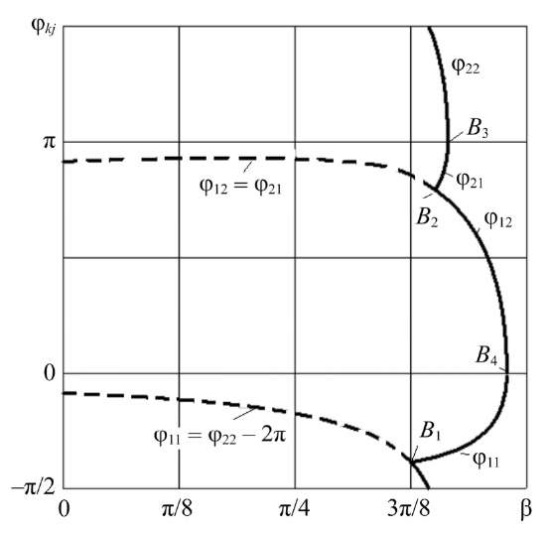
Рис. 1. Зависимости фаз стационарного движения от угла наклона приложенной силы
На рис. 2 представлены зависимости средней скорости твердого тела vm от угла наклона линии действия внешней силы b при коэффициенте трения 0,1 и нескольких амплитудах возбуждения. При любых значениях амплитуды возбуждения и горизонтальном действии силы (b = 0) средняя скорость твердого тела равна нулю. С увеличением b средняя скорость возрастает. Точки смены режимов движения обозначены только на кривой A = 0,6. Для каждого значения амплитуды силы существует оптимальный угол, при котором средняя скорость движения максимальна.
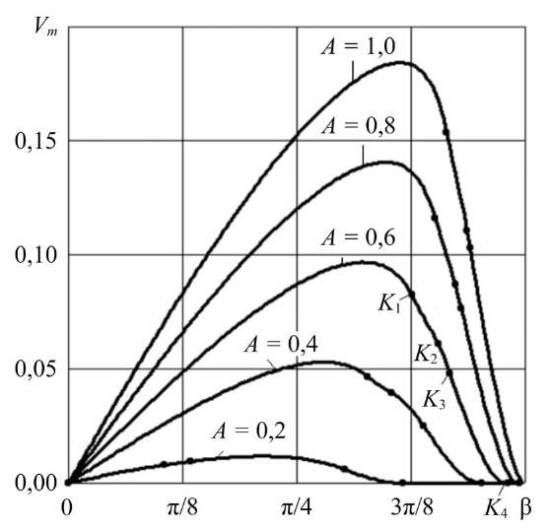
Рис. 2. Зависимость средней скорости Vm от угла b
Обсуждение и заключение. Исследовано движение твердого тела по горизонтальной плоскости под действием гармонической силы, направленной под углом к горизонту. Аналитические и численные результаты показали, что для всех возможных режимов стационарного движения твердого тела определяются четыре фазы. Полученные зависимости фаз стационарного движения и средней скорости движения твердого тела от угла наклона линии действия внешней силы позволяют определить необходимые и оптимальные значения параметров задачи для достижения требуемой скорости движения твердого тела. Показано, что для каждого значения амплитуды силы существует оптимальный угол, при котором средняя скорость движения максимальна.
Полученные результаты могут быть использованы в разработке алгоритмов и проектировании движения робототехнических устройств при движении по горизонтальной плоскости с учетом действия гармонических нагрузок.
Список литературы
1. Черноусько Ф.Л. Плоские движения тела, управляемого при помощи подвижной массы. Доклады Российской Академии наук. Физика, технические науки. 2020;494(1):69–74.
2. Черноусько Ф.Л. Оптимальное управление движением двухмассовой системы. Доклады Академии Наук. 2018;480(5):528–532. https://doi.org/10.7868/S0869565218050043
3. Андронов В.В., Журавлев В.Ф. Сухое трение в задачах механики. Монография. Москва–Ижевск: издательство «ИКИ»; 2010. 184 с.
4. Блехман И.И. Вибрационная механика и вибрационная реология (теория и приложения). Москва: Физматлит; 2018. 751 с.
5. Черноусько Ф.Л. О движении тела, содержащего подвижную внутреннюю массу. Доклады Академии Наук. 2005;405(1):56–60.
6. Черноусько Ф.Л. Анализ и оптимизация движения тела, управляемого посредством подвижной внутренней массы. Прикладная математика и механика. 2006;70(6):915–941.
7. Hongyi Li, Katsuhisa Furuta, Felix L Chernousko. Motion Generation of the Capsubot Using Internal Force and Static Friction. In: Proc. 45th IEEE Conference on Decision and Control. New York City: IEEE; 2006. P. 6575–6580. https://doi.org/10.1109/CDC.2006.377472
8. Нунупаров А.М., Суханов А.Н., Сырых Н.В. Оптимизация средней скорости капсульного робота методом нелинейного модельно-упреждающего управления. В: Труды XXXIII Международной инновационной конференции молодых ученых и студентов по проблемам машиноведения. Москва: Институт машиноведения им. А.А. Благонравова Российской академии наук; 2021. С. 436–441.
9. Сырых Н.В., Нунупаров А.М., Суханов А.Н. К построению математической модели электромагнитной силы соленоида для капсульного робота. В: Труды XXXIII Междунар. инновационной конф. молодых ученых и студентов по проблемам машиноведения. Москва: Институт машиноведения им. А. Благонравова Российской академии наук; 2021. С. 484–490.
10. Болотник Н.Н., Нунупаров А.М., Чащухин В.Г. Капсульный вибрационный робот с электромагнитным приводом и возвратной пружиной: динамика и управление движением. Известия Российской Академии Наук. Теория и системы управления. 2016;(6):146–160.
11. Шматков А.М. Периодические решения задачи оптимального управления поворотом твердого тела с помощью внутренней массы. Вестник Московского университета. Серия 1: Математика. Механика. 2020;(3):63–67. URL: https://www.mathnet.ru/links/3f7d22880247a4d39922b11f27ea3c8c/vmumm4333.pdf (дата обращения: 18.11.2024).
12. Сахаров А.В. Поворот тела с двумя подвижными внутренними массами на шероховатой плоскости. Прикладная математика и механика. 2015;79(2):132–141. URL: https://pmm.ipmnet.ru/ru/Issues.php?y=2015&n=2&p=196 (дата обращения: 18.11.2024).
13. Xiong Zhang, Jian Xu, Hongbin Fang. A Vibration-Driven Planar Locomotion Robot – Shell. Robotica. 2018;36(9):1402–1420. http://doi.org/10.1017/S0263574718000383
14. Черноусько Ф.Л. Движение тела по плоскости под влиянием подвижных внутренних масс. Доклады Академии Наук. 2016;470(4):406–410. https://doi.org/10.7868/S0869565216280070
15. Муницын А.И., Крайнова Л.Н. Вибрационное перемещение твердого тела по наклонной плоскости. Проблемы машиностроения и автоматизации. 2023;(1):31–35.
Об авторах
А. И. МуницынРоссия
Александр Иванович Муницын, доктор технических наук, профессор кафедры робототехники, мехатроники, динамики и прочности машин
111250, г. Москва, ул. Красноказарменная, д. 14, стр. 1
В. Э. Цой
Россия
Валерьян Эдуардович Цой, кандидат физико-математических наук, доцент кафедры робототехники, мехатроники, динамики и прочности машин
111250, г. Москва, ул. Красноказарменная, д. 14, стр. 1
Рецензия
Для цитирования:
Муницын А.И., Цой В.Э. Динамика плоского твердого тела на горизонтальной плоскости. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):7-13. https://doi.org/10.23947/2687-1653-2025-25-1-7-13. EDN: ATOYXO
For citation:
Munitsyn A.I., Tsoy V.E. Dynamics of a Flat Rigid Body on a Horizontal Plane. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):7-13. https://doi.org/10.23947/2687-1653-2025-25-1-7-13. EDN: ATOYXO
JATS XML














































