Перейти к:
Анализ кинематики четвероногого робота при поворотных движениях его корпуса
https://doi.org/10.23947/2687-1653-2025-25-1-14-22
EDN: YINENP
Аннотация
Введение. Шагающие роботы находят широкое применение в промышленности благодаря своим уникальным возможностям передвижения по неровным и сложным поверхностям. Для обеспечения высокой точности управления их движением необходимо разработать математические модели и алгоритмы планирования перемещения робота по различным траекториям. Ключевым аспектом системы управления движением шагающих роботов является планирование перемещений их ног. Несмотря на значительные достижения в области моделирования кинематики четвероногих роботов, в существующих научных публикациях не представлено полноценной кинематической модели для роботов, аналогичных Mini Cheetah. Цель данной работы заключается в разработке кинематической модели четвероногого робота на основе Mini Cheetah, а также в формулировании рекомендаций по оптимизации его походки для обеспечения вращения вокруг различных осей. Создание такой модели позволит улучшить плавность и точность движений робота, что, в свою очередь, повысит его эффективность в реальных производственных условиях.
Материалы и методы. Процесс построения кинематической модели робота основан на использовании формул геометрии пространственного движения твердых тел. Для проверки эффективности предложенных алгоритмов перемещения ног робота при осуществлении поворотных движений его корпуса было применено численное моделирование кинематики робота. Численные расчеты выполнены с использованием математического пакета Wolfram Mathematica.
Результаты исследования. Предложены законы изменения конечных точек ног робота при его вращении вокруг вертикальной оси. Проведенное численное моделирование кинематики робота охватывало повороты корпуса по углам курса, крена и тангажа. По результатам моделирования установлено, что зависимости углов поворота звеньев ног являются периодическими функциями. Рассмотренные поворотные движения платформы робота могут происходить без возникновения сингулярных конфигураций.
Обсуждение и заключение. Результаты численного моделирования поворотных движений платформы робота подтвердили работоспособность предложенного плана переноса ног, который позволяет осуществлять плавное движение корпуса робота и избегать сингулярных конфигураций. Полученная кинематическая модель может быть использована для управления движением робота на кинематическом уровне при перемещениях по криволинейным траекториям. В качестве перспективы для дальнейших исследований стоит выделить разработку математической модели динамики четвероногого робота, а также создание законов управления его движением на динамическом уровне. Это позволит значительно расширить функциональные возможности робота и повысить эффективность его работы в различных условиях эксплуатации.
Ключевые слова
Для цитирования:
Фернандо М.Ж., Сайпулаев Г.Р., Сайпулаев М.Р. Анализ кинематики четвероногого робота при поворотных движениях его корпуса. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):14-22. https://doi.org/10.23947/2687-1653-2025-25-1-14-22. EDN: YINENP
For citation:
Fernando M.J., Saypulaev G.R., Saypulaev M.R. Analysis of a Four-Legged Robot Kinematics during Rotational Movements of Its Body. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):14-22. https://doi.org/10.23947/2687-1653-2025-25-1-14-22. EDN: YINENP
Введение. В настоящее время при решении задач наблюдения и исследования территорий происходит широкое внедрение шагающих мобильных роботов [1]. Примером одной из распространенных конструкций таких роботов является четвероногий робот Mini Cheetah (рис. 1), разработанный в MIT Biomimetic Robotics Lab (https://biomimetics.mit.edu). Указанные четвероногие роботы могут передвигаться по различному типу местности в отличии от колесных или гусеничных роботов.

Рис. 1. Четвероногий робот Mini Cheetah1
Конструкция рассматриваемых шагающих роботов включает в себя платформу, к которой крепятся четыре ноги. Каждая из ног представляет собой трехзвенный манипулятор. Одним из ключевых аспектов шагающего робота является топология конструкции его ног [2][3]. Под топологией ног понимается состав и расположение звеньев, а также шарниров конечностей четвероногого робота, которые играют важную роль в обеспечении его движения и устойчивости. Разработка оптимальной топологии конструкции ног для четвероногих роботов представляет собой одну из сложнейших инженерных задач. Решение этой задачи не только способствует обеспечению устойчивой и эффективной походки (локомоции) робота на различных поверхностях, но и делает его механическую конструкцию более надежной и энергетически эффективной.
Другим аспектом, который необходимо учитывать, является приводная система, используемая в четвероногих роботах [4]. В таких роботах широко используются различные типы приводов, в том числе как пневматические [5], гидравлические [6][7] и электрические [2][6], каждый из которых имеет свои преимущества и недостатки.
Четвероногие роботы обладают сложной кинематикой из-за большого числа степеней свободы. Рассматриваемый в данной работе робот имеет восемнадцать степеней свободы. Для обеспечения успешной локомоции четвероногих роботов необходимо решать прямую, так и обратную задачи кинематики, что позволяет организовывать динамическое управление положением ног этих роботов. Это управление должно обеспечивать балансировку робота, возможность преодоления различных поверхностей и адаптацию к различным видам локомоции, включая ходьбу, бег и скакание. Прямая задача кинематики шаговых роботов заключается в определении положения и ориентации платформы робота на основе известных углов поворота звеньев ног. Обратная задача состоит в нахождении углов поворота звеньев ног, которые обеспечивают заданное положение и ориентацию платформы робота.
В статье [8] подробно изложено применение метода Денавита-Хартенберга для моделирования прямой и обратной кинематики шагающего робота. Проведено исследование кинематической модели робота с целью создания алгоритма походки.
Авторы [9] разработали продвинутые методологии кинематического и динамического моделирования на основе теории винтов (screw theory) для четвероногих роботов. Предложенные методы учитывают различные походки и топологии механизмов ног, используя упрощенные модели контакта стопы (например, модель шарового шарнира). Описаны модели для трех отдельных фаз движения робота: стояние, ходьба и безопорная фаза (полёт). Разработанные стратегии управления используют представленные модели для планирования походки и бега трусцой.
Последние годы ученые работают над системами управления и планирования траектории. Метод управления движением является основой четвероногого робота, напрямую влияющим на гибкость, устойчивость и способность адаптироваться к различным опорным поверхностям [3].
В статье [10] уточняется конструкция регулятора для силового управления четвероногим роботом. Основной целью регулятора ставится выравнивание сил, действующих на робота при симметричной походке, а также снижение возмущению и поглощению ударных воздействий.
В исследовании [11] авторы предложили новую стратегию управления движением четвероногого робота, которая позволяет ему эффективно перемещаться по неровным ландшафтам, независимо от условий визуального восприятия. В [12] рассмотрено создание контроллера движения для четвероногого робота, использующего оптимизацию крутящего момента и контроль производительности с учетом воздействия непредсказуемых внешних сил, таких как неровности поверхности.
Экспериментальные исследования, посвященные применению иерархических контроллеров для управления движением четвероногих роботов, представлены в работе [13] на примере робота ANYmal, а также в [14] на примере робота StarlETH.
Авторы [15] обсуждают разработку четвероногого робота, предназначенного для решения задач в строительстве и ликвидации чрезвычайных ситуаций. В их работе рассматриваются статика, кинематика и система управления для конкретной конструкции данного робота.
Наконец, в исследовании [16] представлен новый контроллер модели центрального генератора шаблонов и тактика переключения походки, основанная на модели Уилсона-Коуэна. Эта разработка направлена на создание плавной походки робота и сокращение времени регулировки в колебательной механической системе.
Несмотря на разработанность задачи моделирования кинематики четвероногих роботов, в существующих публикациях отсутствует полная кинематическая модель движения роботов, конструкция ног которых аналогична роботу Mini Cheetah (рис. 1). Поэтому целью данной работы являлась разработка кинематической модели четвероногого робота на примере Mini Cheetah и выработка предложений по планированию движений звеньев робота, обеспечивающих вращение робота вокруг различных осей.
Для достижения поставленной цели необходимо сформулировать законы изменения координат конечных точек ног робота и угловых координат корпуса. Важно решить обратную задачу кинематики робота для проверки работоспособности предложенного плана движения. Полученные результаты в дальнейшем могут быть использованы для разработки управления роботом на кинематическом уровне.
Материалы и методы. Описание системы. Объектом исследования является роботизированная система, состоящая из твердого тела (платформы робота) и четырех ног с тремя степенями свободы qi = (φi, αi, βi), 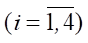 на каждую из ног. Звенья ног связаны с платформой робота несколькими шарнирами, которые приводятся в движение электрическими приводами. Угол βi является углом поворота звена OiAi вокруг продольной оси корпуса робота и характеризует поворот плоскости ноги (содержащей точки Ai, Bi, Ki) относительно вертикальной плоскости симметрии CXZ. А углы αi, βi характеризуют поворот звеньев AiBi и BiKi в плоскости ноги. Шарниры звеньев ног в точках Oi, Ai, Bi являются управляемыми, то есть поворот звеньев ног на углы φi, αi, βi обеспечивается независимо соответствующими приводами.
на каждую из ног. Звенья ног связаны с платформой робота несколькими шарнирами, которые приводятся в движение электрическими приводами. Угол βi является углом поворота звена OiAi вокруг продольной оси корпуса робота и характеризует поворот плоскости ноги (содержащей точки Ai, Bi, Ki) относительно вертикальной плоскости симметрии CXZ. А углы αi, βi характеризуют поворот звеньев AiBi и BiKi в плоскости ноги. Шарниры звеньев ног в точках Oi, Ai, Bi являются управляемыми, то есть поворот звеньев ног на углы φi, αi, βi обеспечивается независимо соответствующими приводами.
Вводится неподвижная система координат XYZ и подвижная система координат Cxyz, где точка C — геометрический центр платформы робота (рис. 2 a). Ориентация платформы робота описывается углами курса ψ (поворот вокруг оси z), крена θ (поворот вокруг оси x) и тангажа γ (поворот вокруг оси y), а положение платформы робота определяется координатами геометрического центра xC, yC и zC в неподвижной системе координат.
Расстояния вдоль продольной и поперечной осей платформы робота от центра масс C и точками крепления ног к платформе робота Oi в подвижных осях xiyizi задаются ρxi и ρyi. Длины звеньев обозначены, как
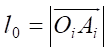 ,
, 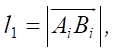
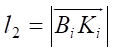
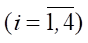 (рис. 2 б).
(рис. 2 б).
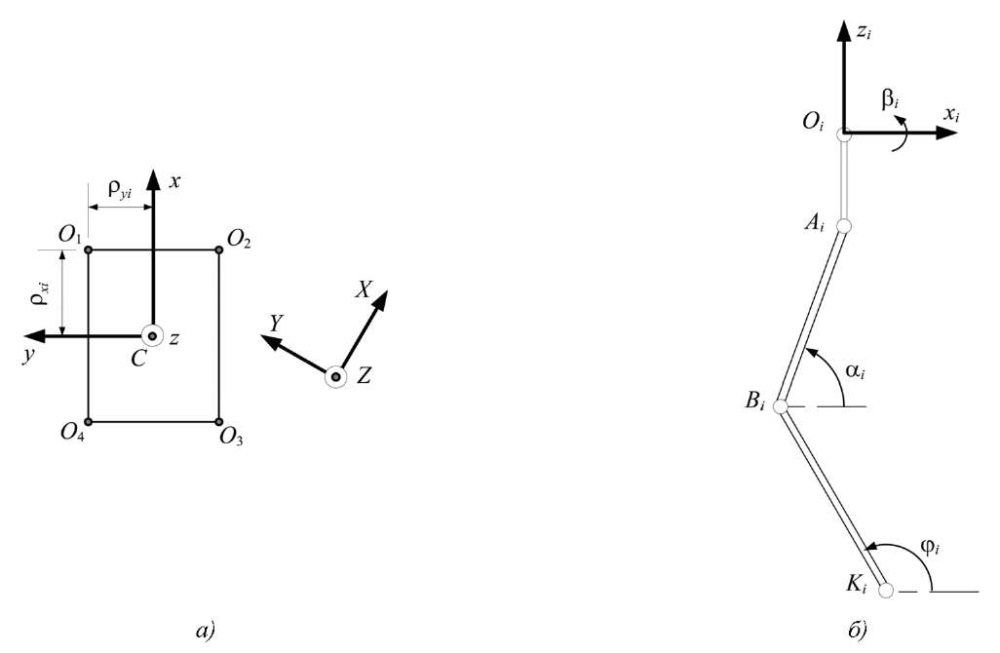
Рис. 2. Кинематическая схема робота:
а — вид сверху на корпус робота; б — вид сбоку на ногу робота
Кинематическое моделирование робота. В проекциях на оси неподвижной системы координат XYZ вектор положения конечной точки ноги Ki (или точки, контактирующей с поверхностью) определяется формулой:
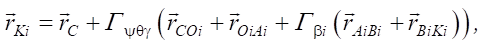 (1)
(1)
где 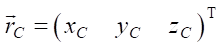 — вектор положения геометрического центра платформы робота C; Гψγθ = ГψГθГγ — матрица поворота, которая вычисляется как произведения матриц элементарных поворотов на углы курса, крена и тангажа. Матрицы поворота, входящие в уравнение (1), имеют вид:
— вектор положения геометрического центра платформы робота C; Гψγθ = ГψГθГγ — матрица поворота, которая вычисляется как произведения матриц элементарных поворотов на углы курса, крена и тангажа. Матрицы поворота, входящие в уравнение (1), имеют вид:
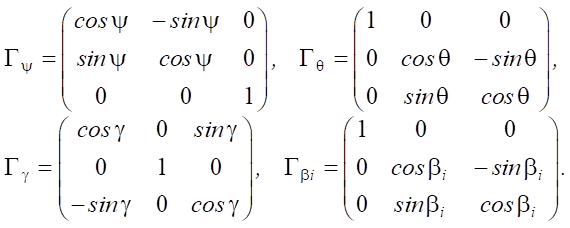 (2)
(2)
Другие радиус-вектора, входящие в уравнение (1), определяются выражениями:
 (3)
(3)
здесь верхний индекс «T» означает операцию транспонирования вектора.
После выполнения промежуточных вычислений в правой части уравнения (1), с учетом выражений (2) и (3), получим проекции вектора положений 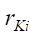 для каждой ноги.
для каждой ноги.
Дифференцируя уравнение (1) по времени, получим кинематическую модель в виде:
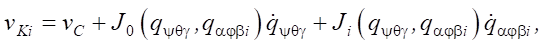 (4)
(4)
где 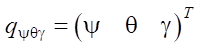 — вектор угловых обобщенных координат платформы робота;
— вектор угловых обобщенных координат платформы робота; 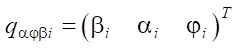 — вектор угловых обобщенных координат звеньев ног робота;
— вектор угловых обобщенных координат звеньев ног робота; 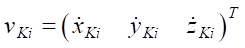 — вектор линейной скорости конечной точки i-ой ноги;
— вектор линейной скорости конечной точки i-ой ноги; 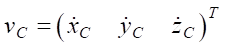 — вектор линейной скорости геометрического центра платформы робота;
— вектор линейной скорости геометрического центра платформы робота; 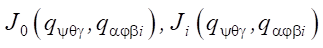 — матрицы коэффициентов для соответствующих векторов обобщенных скоростей.
— матрицы коэффициентов для соответствующих векторов обобщенных скоростей.
Результаты исследования. Для анализа поворотных движений робота посредством решения уравнений геометрии движения (1) (или интегрирования кинематических уравнений (4)) зададимся начальными условиями для углов поворота звеньев ног и законами изменения скоростей конечных точек ног vKi, геометрического центра платформы робота vC и вектора угловых обобщенных координат qψθγ. Рассматривая поворотные движения платформы робота, положим геометрический центр неподвижным в процессе движения vC = 0.
В качестве начальной позиции звеньев ног примем следующие значения углов φi, αi, βi 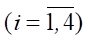 для каждой из ног:
для каждой из ног:
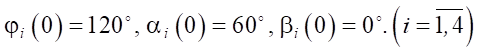 (5)
(5)
Приведенное сочетание значений углов φi, αi, βi 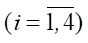 соответствует положению стояния робота на полусогнутых ногах, которое представлено на упрощенной визуализации (рис. 3), выполненной в Wolfram Mathematica. При визуализации были использованы следующие значения геометрических параметров робота: l0 = 0,15 м, l1 = 0,45 м, l2 = 0,45 м, ρx1 = ρx2 = –ρx3 = –ρx4 = 0,5 м, ρy1 = –ρy2 = –ρy3 = ρy4 = 0,25 м.
соответствует положению стояния робота на полусогнутых ногах, которое представлено на упрощенной визуализации (рис. 3), выполненной в Wolfram Mathematica. При визуализации были использованы следующие значения геометрических параметров робота: l0 = 0,15 м, l1 = 0,45 м, l2 = 0,45 м, ρx1 = ρx2 = –ρx3 = –ρx4 = 0,5 м, ρy1 = –ρy2 = –ρy3 = ρy4 = 0,25 м.
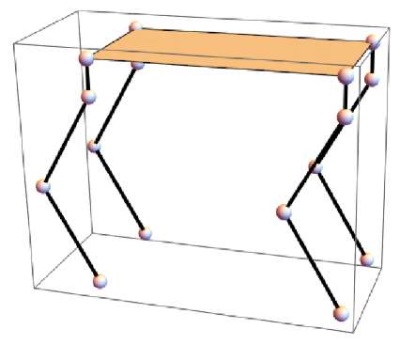
Рис. 3. Упрощенная визуализация начального положения робота
Для выполнения периодических поворотных движений платформы робота, ограниченных только углом крена, задаем законы изменения углов ориентации платформы в виде:
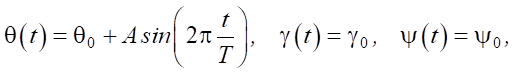 (6)
(6)
где ψ0 = 0°, θ0 = 0°, γ0 = 0° — начальные значения углов ориентации; A = 0,2 рад и Т = 20 с — постоянные, характеризующие амплитуду и период колебаний по углу. Поскольку при повороте платформы робота по углу крена перенос ног является необязательным, то координаты точек контакта ног с опорной поверхностью остаются неизменными (vKi = 0):
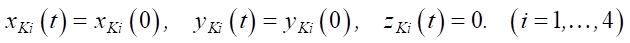 , (7)
, (7)
где xKi(0) и yKi(0) — начальные координаты точек контакта ног робота с опорной поверхностью.
Решая уравнения (1) с учетом (2) и (3) при подстановке программного движения (6) и (7), получим зависимости углов поворота φi, αi, βi звеньев ног (рис. 4).
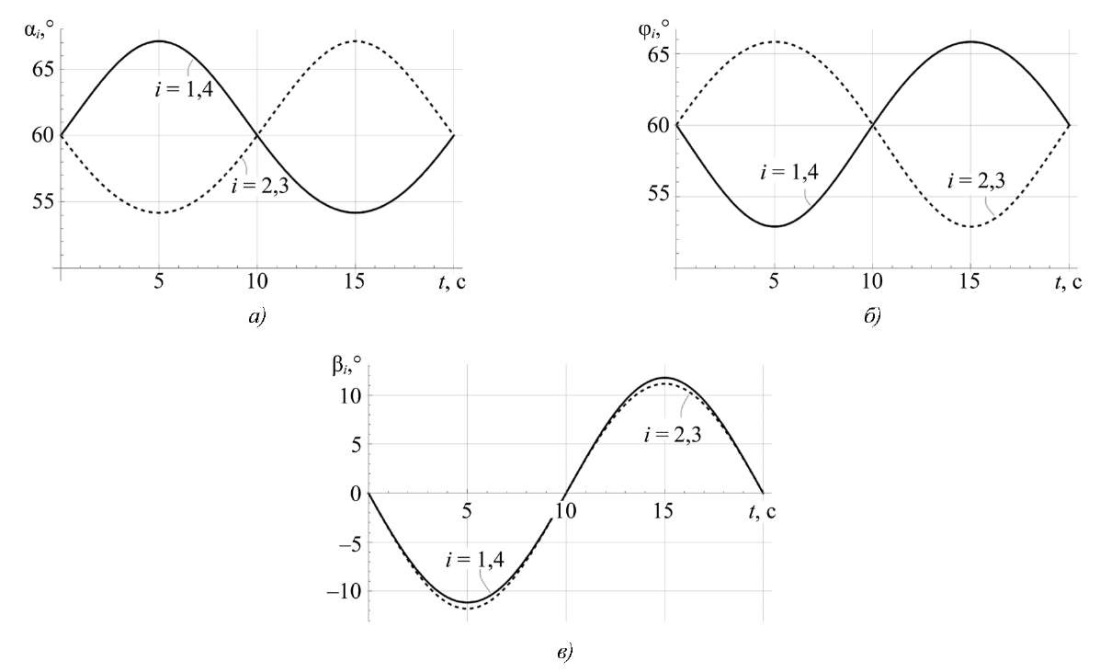
Рис. 4. Результаты моделирования поворотов по углу крена:
а — углы αi(t); б — углы φi(t); в — углы βi(t)
По результатам моделирования, представленном на рис. 4, можно отметить, что углы поворота звеньев ног являются гармоническими функциями. Как следствие, можно отметить, что повороты платформы робота вокруг продольной оси симметрии робота (6) могут осуществляться без отрыва точек контакта ног от поверхности.
Для выполнения периодических поворотных движений платформы робота только по углу тангажа задаем законы изменения углов ориентации платформы в виде:
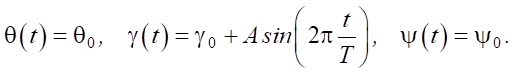 (8)
(8)
При повороте платформы робота по углу тангажа перенос ног является необязательным, и координаты точек контакта ног с опорной поверхностью остаются неизменными.
Решая уравнения (1) с учетом (2) и (3) подставляя программные движения (7) и (8), получим зависимости углов поворота φi, αi, βi звеньев ног (рис. 5).
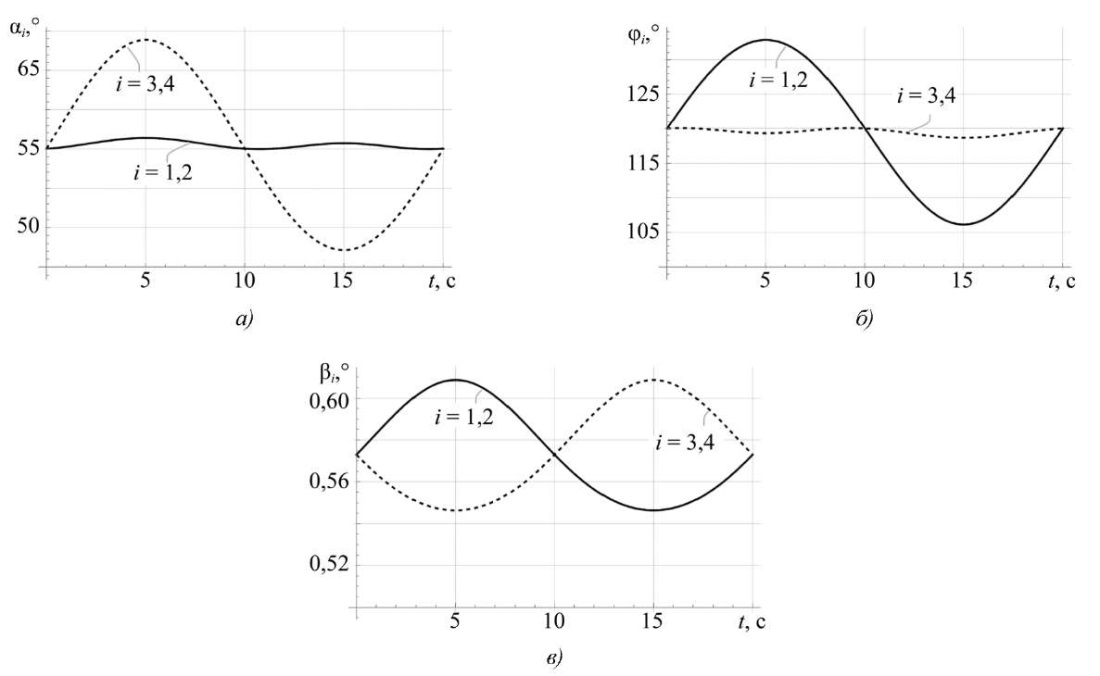
Рис. 5. Результаты моделирования поворотов по углу тангажа:
а — углы αi(t); б — углы φi(t); в — углы βi(t)
По результатам моделирования, представленным на рис. 5, можно отметить, что углы поворота звеньев ног являются гармоническими функциями. Как следствие, можно отметить, что повороты платформы робота вокруг поперечной оси симметрии робота (8) могут быть осуществлены без отрыва точек контакта ног от поверхности.
Для выполнения поворота вокруг оси Z рассмотрим законы изменения углов ориентации платформы робота в виде:
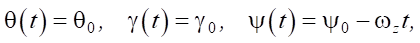 (9)
(9)
где ωz = 0,085 рад/с угловая скорость поворота платформы робота.
Для обеспечения вращения робота вокруг вертикальной оси необходимо спланировать перемещение ног. Рассмотрим случай, когда траектории точек контакта ног в проекциях на горизонтальную плоскость XY будут принадлежать окружности радиуса ρ. При этом будем считать, что ось, вокруг которой будет происходить вращение платформы робота, проходит через геометрический центр платформы. Тогда выражения для координат конечных точек ног можно определить из соотношений:
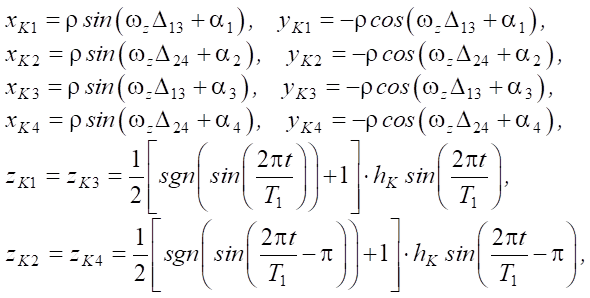 (10)
(10)
где 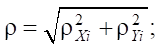
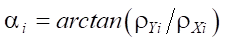 — угол, характеризующий положение конечной точки i-ой ноги в начальный момент времени; hK = 0,3 м — максимальная высота, на которую поднимаются конечные точки ног робота; T1 = 6 с — время одного шага; Δ13, Δ24 — вспомогательные функции, используемые для обеспечения кусочного задания изменения координат конечных точек ног:
— угол, характеризующий положение конечной точки i-ой ноги в начальный момент времени; hK = 0,3 м — максимальная высота, на которую поднимаются конечные точки ног робота; T1 = 6 с — время одного шага; Δ13, Δ24 — вспомогательные функции, используемые для обеспечения кусочного задания изменения координат конечных точек ног:
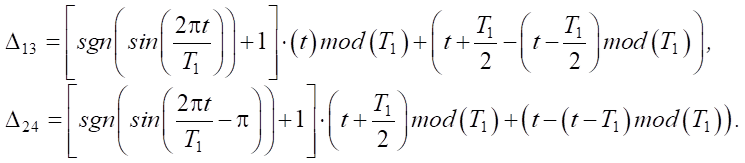 (11)
(11)
Здесь функция (t)mod(T1) возвращает остаток от целочисленного деления t на T1. Кусочный характер задания изменения координат связан с рассмотрением гейтов (элементарных движений ног), при которых выполняется последовательный перенос накрестлежащих ног.
Решая уравнения (1) с учетом (2) и (3) при подстановке программного движения (9)–(11), получим зависимости углов поворота φi, αi, βi звеньев ног (рис. 6).
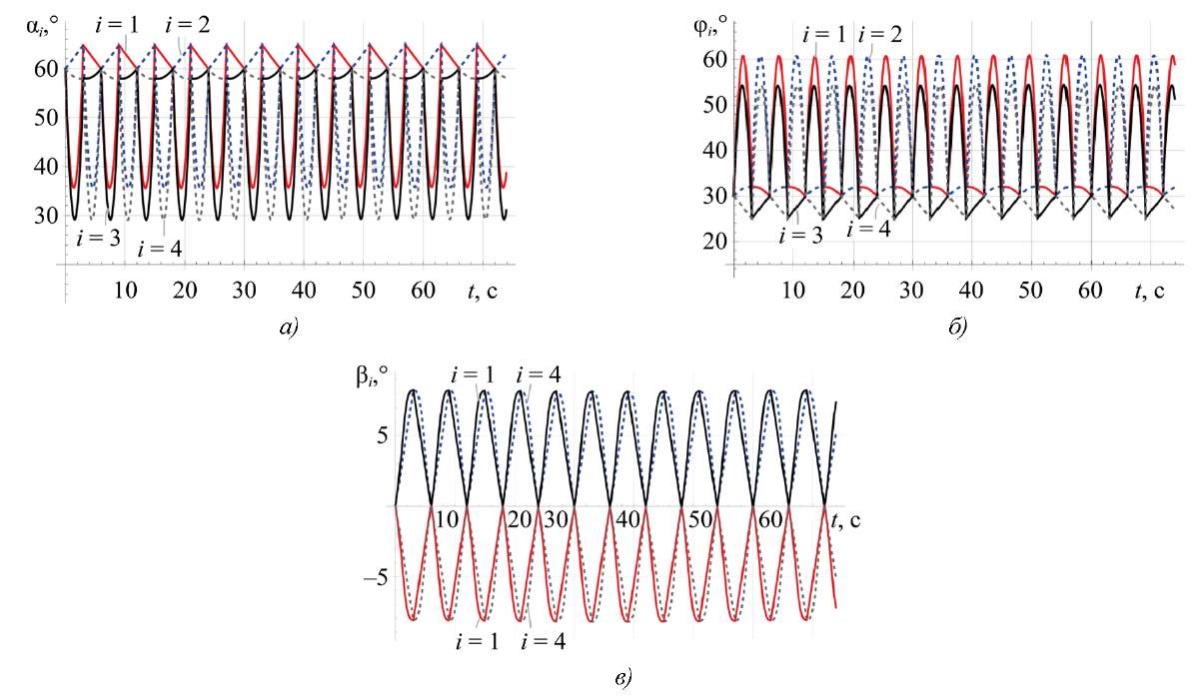
Рис. 6. Результаты моделирования поворотов по углу курса:
а — углы αi(t); б — углы φi(t); в — углы βi(t)
По результатам моделирования видно, что зависимости углов поворота звеньев ног являются периодическими функциями и, как следствие, рассмотренные поворотные движения платформы робота могут происходить без возникновения сингулярных конфигураций. Таким образом, предложенный план переноса ног (10), (11) при вращении вокруг вертикальной оси Z является пригодным для осуществления поворота робота на произвольный угол ψ.
Обсуждение и заключение. Построенная математическая модель кинематики позволяет определить углы в сочленениях звеньев ног робота, которые необходимо обеспечить для реализации желаемого движения платформы робота. Полученные результаты численного моделирования поворотных движений корпуса робота подтвердили работоспособность разработанной кинематической модели для оценки реализации заданных движений робота с учетом ограничений и размеров конструкции.
В случаях, когда платформа робота осуществляет плоское движение (при нулевых значениях углов тангажа и крена), построенная математическая модель кинематики совпадает с опубликованными результатами других авторов. Полученные в данной работе результаты являются обобщением и уточнением уравнений, связывающих углы поворота звеньев ног робота с положением и ориентацией платформы робота.
Применение разработанной кинематической модели (1), (4), а также предложенного плана переноса ног (10), (11) при вращении вокруг вертикальной оси, позволит построить управление на кинематическом уровне для передвижения робота по криволинейным траекториям. Данный подход существенно расширит функциональные возможности робота и повысит эффективность его работы в различных условиях эксплуатации.
1. Massachusetts Institute of Technology. URL: https://news.mit.edu/2019/mit-mini-cheetah-first-four-legged-robot-to-backflip-0304 (дата обращения: 07.11.2024).
Список литературы
1. Павловский В.Е. О разработках шагающих машин. Препринты ИПМ им. М.В. Келдыша. 2013;(101):1–32. URL: https://keldysh.ru/papers/2013/prep2013_101.pdf (дата обращения: 20.11.2024).
2. Taheri H, Mozayani N. A Study on Quadruped Mobile Robot. Mechanism and Machine Theory. 2023;190:105448. https://doi.org/10.1016/j.mechmachtheory.2023.105448
3. Hui Chai, Yibin Li, Rui Song, Guoteng Zhang, Qin Zhang, Song Liu, et al. A Survey of the Development of Quadruped Robots: Joint Configuration, Dynamic Locomotion Control Method and Mobile Manipulation Approach. Biomimetic Intelligence and Robotics. 2022;2(1):100029. https://doi.org/10.1016/j.birob.2021.100029
4. Liang ZJ, Jiang L, Zhao JX, Xing BY, Xu P, Su B. Design and Analysis of High Dynamic Actuator and Implementation on Quadruped Robot. Journal of Physics: Conferences Series. 2023;2478:102002. https://doi.org/10.1088/1742-6596/2478/10/102002
5. Jiupeng Chen, Hongjun San, Xing Wu. Gait Regulation of a Bionic Quadruped Robot with Antiparallelogram Leg Based on CPG Oscillator. Complexity. 2019;2019(5):5491298. https://doi.org/10.1155/2019/5491298
6. Khan H, Kitano S, Frigerio M, Camurri M, Barasuol V, Featherstone R, et al. Development of the Lightweight Hydraulic Quadruped Robot — MiniHyQ. In: Proceedings of the 2015 IEEE International Conference on Technologies for Practical Robot Applications (TePRA). New York City: IEEE; 2015. P. 1–6. https://doi.org/10.1109/TePRA.2015.7219671
7. Lizhou Fang, Junhui Zhang, Huaizhi Zong, Ximeng Wang, Kun Zhang, Jun Shen, et al. Open-Source Lower Controller for Twelve Degrees of Freedom Hydraulic Quadruped Robot with Distributed Control Scheme. HardwareX. 2023;13:e00393. https://doi.org/10.1016/j.ohx.2022.e00393
8. Yunde Shi, Shilin Li, Mingqiu Guo, Yuan Yang, Dan Xia, Xiang Luo. Structural Design, Simulation and Experiment of Quadruped Robot. Applied Sciences. 2021;11(22):10705. https://doi.org/10.3390/app112210705
9. Wei Yan, Yang Pan, Junjie Che, Jiexian Yu, Zhuchen Han. Whole-Body Kinematic and Dynamic Modeling for Quadruped Robot under Different Gaits and Mechanism Topologies. PeerJ Computer Science. 2021;7(1):e821. https://doi.org/10.7717/peerj-cs.821
10. Havoutis I, Semini C, Buchli J, Caldwell DG. Quadrupedal Trotting with Active Compliance. In: Proceedings of the 2013 IEEE International Conference on Mechatronics (ICM). New York City: IEEE; 2013. P. 610–616. https://doi.org/10.1109/ICMECH.2013.6519112
11. Jiawei Chen, Kun Xu, Xilun Ding. Adaptive Gait Planning for Quadruped Robot Based on Center of Inertia over Rough Terrain. Biomimetic Intelligence and Robotics. 2021;2(1):100031. https://doi.org/10.1016/j.birob.2021.100031
12. Guiyang Xin, Wolfslag W, Hsiu-Chin Lin, Tiseo C, Mistry M. An Optimization-Based Locomotion Controller for Quadruped Robots Leveraging Cartesian Impedance Control. Frontiers in Robotics and AI. 2020;7:48. https://doi.org/10.3389/frobt.2020.00048
13. Bellicoso CD, Gehring C, Hwangbo J, Fankhauser P, Hutter M. Perception-less Terrain Adaptation through Whole Body Control and Hierarchical Optimization. In: Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids). New York City: IEEE; 2017. P. 558–564. https://doi.org/10.1109/HUMANOIDS.2016.7803330
14. Hutter M, Sommer H, Gehring C, Hoepflinger M, Bloesch M, Siegwart R. Quadrupedal Locomotion Using Hierarchical Operational Space Control. The International Journal of Robotics Research. 2014;33(8):1047–1062. https://doi.org/10.1177/0278364913519834
15. Zhao Z, Noritsugu T, Takaiwa M, Sasaki D. Development of Quadruped Robot with Pneumatic Actuator. In: Proceedings of the 8th International Symposium on Fluid Power. New York City: IEEE; 2010. P. 325–330. https://doi.org/10.1299/jsmeicam.2010.5.325
16. Junmin Li, Jinge Wang, Simon X Yang, Kedong Zhou, Huijuan Tang. Gait Planning and Stability Control of a Quadruped Robot. Computational Intelligence and Neuroscience. 2016:2016;9853070. https://doi.org/10.1155/2016/9853070
Об авторах
М. Ж. ФернандоРоссия
Марселино Жулио Фернандо, студент кафедры робототехники, мехатроники, динамики и прочности машин
Scopus ID: 59000562600
111250, г. Москва, ул. Красноказарменная, д. 14, стр. 1
Г. Р. Сайпулаев
Россия
Гасан Русланович Сайпулаев, кандидат технических наук, старший преподаватель кафедры робототехники, мехатроники, динамики и прочности машин
Scopus ID: 57222571340
111250, г. Москва, ул. Красноказарменная, д. 14, стр. 1
М. Р. Сайпулаев
Россия
Муса Русланович Сайпулаев, кандидат технических наук, старший преподаватель кафедры робототехники, мехатроники, динамики и прочности машин
Scopus ID: 57382428600
111250, г. Москва, ул. Красноказарменная, д. 14, стр. 1
Рецензия
Для цитирования:
Фернандо М.Ж., Сайпулаев Г.Р., Сайпулаев М.Р. Анализ кинематики четвероногого робота при поворотных движениях его корпуса. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):14-22. https://doi.org/10.23947/2687-1653-2025-25-1-14-22. EDN: YINENP
For citation:
Fernando M.J., Saypulaev G.R., Saypulaev M.R. Analysis of a Four-Legged Robot Kinematics during Rotational Movements of Its Body. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):14-22. https://doi.org/10.23947/2687-1653-2025-25-1-14-22. EDN: YINENP












































