Перейти к:
Анализ управляемости и оптимизация формы сопла гидропушки на основе прямого экстремального подхода
https://doi.org/10.23947/2687-1653-2025-25-1-65-76
EDN: RVWIZA
Аннотация
Введение. Анализ управляемости является необходимым этапом для корректной постановки и решения любой задачи оптимального управления. Эта проблема становится особенно актуальной в рамках оптимизации систем с распределенными параметрами, которые описываются уравнениями в частных производных. К таким задачам относится рассматриваемая задача оптимизации формы сопла гидропушки. Оптимальное сопло должно обеспечивать максимальное значение функционала, выражаемого через среднюю силу импульса струи гидропушки. Актуальность данного исследования обусловлена отсутствием единого подхода к анализу управляемости систем с распределёнными параметрами, что затрудняет корректную постановку и решение задач оптимизации. В частности, предыдущие попытки решения задачи оптимизации сопла гидропушки с использованием классического вариационного исчисления не увенчались успехом из-за игнорирования аспектов управляемости. Целью данной работы являлось применение нового подхода, предложенного Толстых В.К., к анализу управляемости для решения задачи оптимального дизайна формы сопла гидропушки.
Материалы и методы. В качестве метода исследования использовался анализ управляемости, основанный на условной корректности по Тихонову обратной задачи. Такой подход позволил выявить условия существования градиента целевого функционала и построить регуляризацию решения обратной задачи адаптивными градиентными методами. Это актуально для многоэкстремальных задач, в том числе для задачи оптимальной формы сопла. Она решалась прямым экстремальным подходом в виде непосредственной максимизации целевого функционала на основе его градиента. В процессе исследования использовалась нелинейная, квазиодномерная математическая модель изоэнтропического течения воды в сопле гидропушки. Течение при этом считалось невязким, сжимаемым и дозвуковым.
Результаты исследования. В рамках исследования были получены условия управляемости, которые позволили радикально упростить задачу оптимизации формы сопла гидропушки. Установлено, что для корректного определения градиента целевого функционала необходимо сузить область решения сопряженной задачи до малой прямоугольной области. Использование адаптивных градиентных методов с удовлетворительными шаговыми множителями обеспечило регуляризацию решения. Впервые были найдены две оптимальные формы сопла гидропушки. Первая форма обеспечивает локальный максимум целевого функционала, вторая — глобальный максимум функционала при ограничении на расширение сопла.
Обсуждение и заключение. Полученные результаты показывают, что направленный поиск оптимального решения невозможно осуществить по производной Фреше без учета условий управляемости. Впервые предложенный подход, в сочетании с необходимыми адаптивными градиентными методами оптимизации, позволил не только корректно поставить задачу оптимизации, но и найти оптимальные формы сопла, обеспечивающие максимальную среднюю силу импульса ультраструи. В некоторых случаях для обеспечения устойчивости решения потребовалось введение ограничения на расширение сопла за пределы ствола гидропушки. Это позволило выполнить требования теоремы об управляемости и гарантировало корректность полученных результатов. Теоретическая значимость приведенного исследования заключается в развитии методов анализа управляемости для систем с распределенными параметрами, что создает новые возможности для решения схожих задач в других областях. Результаты работы могут быть применены для оптимизации устройств, работающих на основе импульсных струй, а также для дальнейшего исследования более сложных моделей течения жидкости.
Ключевые слова
Для цитирования:
Толстых В.К., Дмитрук Ю.В. Анализ управляемости и оптимизация формы сопла гидропушки на основе прямого экстремального подхода. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):65-76. https://doi.org/10.23947/2687-1653-2025-25-1-65-76. EDN: RVWIZA
For citation:
Tolstykh V.K., Dmitruk Yu.V. Controllability Analysis and Optimization of Hydrocannon Nozzle Shape Based on Direct Extreme Approach. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):65-76. https://doi.org/10.23947/2687-1653-2025-25-1-65-76. EDN: RVWIZA
Введение. Несмотря на значительное количество исследований в области теории управления, до сих пор отсутствует единый подход к анализу управляемости для систем с распределенными параметрами. Существующие работы, как правило, ограничиваются рассмотрением управляемости как возможности перевода системы из начального состояния в заданное финальное [1]. Однако такой подход оказывается недостаточным для задач оптимизации пространственно-распределенных систем, описываемых уравнениями в частных производных. Управляемость по финальному состоянию не гарантирует управляемость по условиям, заданным в целевом функционале, что делает анализ таких систем сложным и неочевидным. В данной работе авторы предлагают использовать понятие управляемости, предложенное Толстых В.К. [2], и применить его для поиска оптимальной формы сопла гидропушки.
Гидропушки, предназначенные для формирования импульсных струй жидкости высокого давления, находят широкое применение, например, в горной промышленности для разрушения горных пород [3]. Эффективность таких устройств во многом зависит от формы сопла [4], что делает задачу его оптимизации актуальной. Несмотря на значительный интерес к этой проблеме, существующие исследования, такие как работы Зуйковой З. Г. [5], Зубова В.И. [6] и Атанова Г. А. [7], носят преимущественно теоретический характер. Авторы этих работ формулировали необходимые условия оптимальности, однако численные результаты не подтверждались доказательствами их оптимальности. Более того, как будет показано в данной работе, ранее полученные «оптимальные» формы сопел не являются таковыми. Таким образом, несмотря на многолетние исследования, проблема дизайна оптимальной формы сопла остается нерешенной.
Решение этой сложной задачи возможно только при использовании прямого экстремального подхода с оригинальными адаптивными градиентными методами, описанными в работе Толстых В.К. [8]. Целью данной работы являлось применение нового подхода, предложенного в работе [2], к анализу управляемости системы с распределенными параметрами для задачи оптимального дизайна формы сопла гидропушки. Таким образом, статья направлена на развитие теории управляемости для систем с распределенными параметрами и демонстрацию ее практической применимости на примере оптимизации формы сопла гидропушки.
Материалы и методы. Суть прямого экстремального подхода заключается в непосредственной максимизации градиентными методами некоторого целевого функционала:
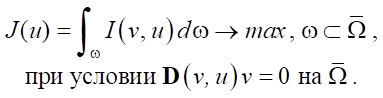 , (1)
, (1)
Здесь управление (в нашем случае — функция формы сопла по длине x) u(x) ∈ U(S), S = (xa, xb) — область определения управления, U — допустимое множество управлений, v(x, t) ∈ V(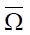 ) — состояние нестационарного процесса формирования ультраструи на замкнутом пространственно-временном множестве {x, t} =
) — состояние нестационарного процесса формирования ультраструи на замкнутом пространственно-временном множестве {x, t} = 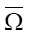 . Оператор
. Оператор 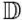 включает в себя конкретный вид дифференциальных уравнений течения воды в гидропушке и действует на v. Функция цели I(v, u) определена на множестве ω, а ее значение явно зависит от параметров v и u.
включает в себя конкретный вид дифференциальных уравнений течения воды в гидропушке и действует на v. Функция цели I(v, u) определена на множестве ω, а ее значение явно зависит от параметров v и u.
В прямом подходе не используются какие-либо промежуточные (например, необходимые условия оптимальности), а непосредственно решается задача:
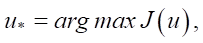 (2)
(2)
где u* — оптимальное управление.
Исходная задача с уравнениями распределенной системы 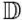 (v, u)v = 0 характеризуется прямым отображением:
(v, u)v = 0 характеризуется прямым отображением:
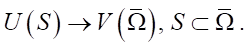
В то же время задача оптимизации (1) является обратной. Такие задачи, как правило, некорректны в классическом смысле [9]. Решение прямых и обратных задач существенно различается. Последние требуют регуляризации решения до сужения множества возможных решений U до компакта корректности 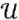 ⊆ U что приводит к условной корректности по Тихонову. В прямом экстремальном подходе регуляризация осуществляется градиентными методами.
⊆ U что приводит к условной корректности по Тихонову. В прямом экстремальном подходе регуляризация осуществляется градиентными методами.
Согласно определению управляемости [2], распределенная система в задаче (1) будет управляема посредством u(x) ∈ U(S) относительно целевого функционала J, когда корректной по Тихонову будет обратная задача отображения элементов пространства V(ω) состояний модели в элемент u* при условии max J:
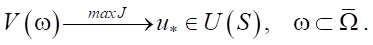
Далее, при решении задачи (2), сделаем анализ управляемости и получим условия управляемости, которые позволят корректно поставить и решить задачу оптимизации формы сопла гидропушки градиентными методами [10].
В работе [8] подробно описана постановка рассматриваемой задачи для дозвуковых, осесимметричных течений сжимаемой жидкости в плавно меняющихся каналах. Напомним ее в форме, необходимой для дальнейших исследований. Изоэнтропическое движение воды в сопле описывается квазиодномерной, квазилинейной гиперболической системой уравнений [11]:
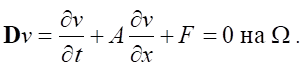 (3)
(3)
Состояние системы характеризуется вектор-функцией v = {ρ, w} ∈ V(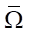 ), где ρ — плотность воды, w — скорость воды. Оператор
), где ρ — плотность воды, w — скорость воды. Оператор 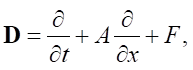 его матрица
его матрица 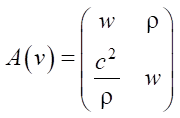 и вектор
и вектор 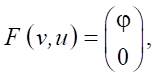 φ = ρwuΘ(x – xa), Θ — тета-функция Дирака, xa — начало сопла в конце ствола гидропушки,
φ = ρwuΘ(x – xa), Θ — тета-функция Дирака, xa — начало сопла в конце ствола гидропушки, 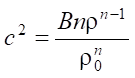 — квадрат скорости звука в воде, B и n — постоянные в уравнении состояния воды в форме Тета.
— квадрат скорости звука в воде, B и n — постоянные в уравнении состояния воды в форме Тета.
Управление описывается формулой:
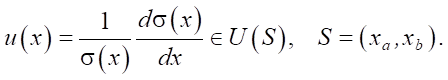 (4)
(4)
Здесь σ — площадь поперечного сечения сопла, 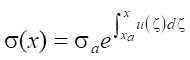 , x ∈ [xa, xb], σa = σ(xa). В стволе гидропушки при x ≤ xa управление u(x) отсутствует, а свободный член φ = 0.
, x ∈ [xa, xb], σa = σ(xa). В стволе гидропушки при x ≤ xa управление u(x) отсутствует, а свободный член φ = 0.
Граничные и начальные условия задачи (3):
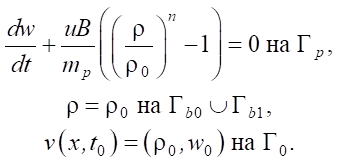
Здесь mp — масса поршня, ρ0 — плотность воды при атмосферном давлении, w0 — скорость воды и поршня до начала втекания в сопло. Границы процесса Г для области Ω показаны на рис. 1. Вид Ω важен для анализа управляемости.
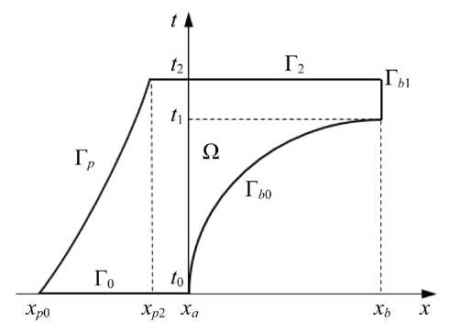
Рис. 1. Область течения воды в гидропушке
Уточним Ω. Начало координат совмещено со входом в сопло xa, a t0 — время начала втекания воды в сопло. С одной стороны, вода ограничена поршнем, движущимся в стволе гидропушки по траектории Гp, а с другой — свободной поверхностью втекания Гb0 от t0 до t1 и истечения Гb1 от t1 до t2. Линия начального состояния системы (3) — это Г0, координаты xp0 и xp2 — начальное и конечное положение поршня. Указанные Г-линии для Ω образуют замыкание 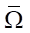 . Область определения управления
. Область определения управления 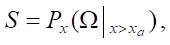 т. е. при x > xa S является проекцией части области Ω на ось x.
т. е. при x > xa S является проекцией части области Ω на ось x.
Задача оптимизации (оптимального дизайна формы сопла) формулируется следующим образом: необходимо найти управление u(x), доставляющее максимум функционалу:
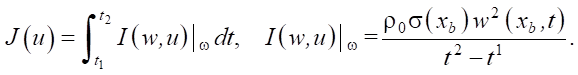 (5)
(5)
Целевой функционал задается на ω = Гb1, т. е. на срезе сопла гидропушки и определяет среднюю силу действия струи на возможную преграду [12].
Градиентный алгоритм для максимизации функционала (5) имеет вид:
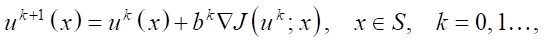 (6)
(6)
где k — номер итерации; bk— шаговый множитель, регулирующий подъем к max J в направлении градиента ∇Jk.
Градиент представляет собой функциональную производную Фреше 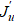 которую можно найти из первой вариации целевого функционала
которую можно найти из первой вариации целевого функционала 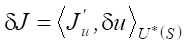 . Здесь угловые скобки означают скалярное произведение, в данном случае — в сопряженном пространстве управлений U*(S). Верхний индекс * означает сопряженность.
. Здесь угловые скобки означают скалярное произведение, в данном случае — в сопряженном пространстве управлений U*(S). Верхний индекс * означает сопряженность.
Следует отметить, что иногда градиент функционала на Гильбертовом пространстве путают с производной Фреше этого функционала [13]. Производная 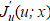 может быть нечувствительна к управлению u(x) на всем множестве S или на частях S ненулевой меры. Поэтому в общем случае
может быть нечувствительна к управлению u(x) на всем множестве S или на частях S ненулевой меры. Поэтому в общем случае 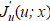 в (6) не будет указывать достоверное направление коррекции uk для направленного поиска оптимального решения u*(x). Градиент из производной Фреше можно получить только при реализации условий управляемости.
в (6) не будет указывать достоверное направление коррекции uk для направленного поиска оптимального решения u*(x). Градиент из производной Фреше можно получить только при реализации условий управляемости.
Ранее упоминались подходы к решению задач оптимизации сопла гидропушки с целью максимизации средней силы импульса струи [5], функционала, зависящего от параметров течения [6], а также максимизации скорости истечения [7]. В этих работах после варьирования δJ получено формальное выражение для производной 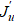 . Оно зависит от решения
. Оно зависит от решения 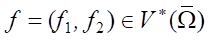 линейной сопряженной гиперболической задачи:
линейной сопряженной гиперболической задачи:
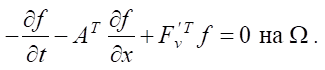 (7)
(7)
Верхний индекс T означает транспонирование, 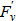 — производная свободного члена F по v. Граничные и начальные (терминальные на Г2) условия:
— производная свободного члена F по v. Граничные и начальные (терминальные на Г2) условия:
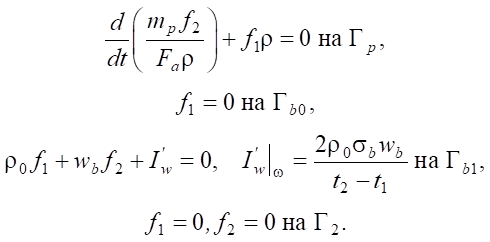
Производную Фреше 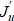 иногда называют невязкой или градиентом. Ее удобнее представить в операторном виде:
иногда называют невязкой или градиентом. Ее удобнее представить в операторном виде:
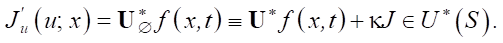 (8)
(8)
Здесь сопряженный неоднородный оператор 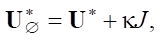
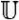 *— сопряженный однородный оператор, точка означает место аргумента f операторов, κ — весовой коэффициент выравнивания вычислительных помех численного решения исходной и сопряженной задач [8]. В выражении (8) присутствует значение функционала в виде числа J. Это значение производной
*— сопряженный однородный оператор, точка означает место аргумента f операторов, κ — весовой коэффициент выравнивания вычислительных помех численного решения исходной и сопряженной задач [8]. В выражении (8) присутствует значение функционала в виде числа J. Это значение производной 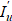 .
.
Неоднородность оператора 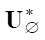 — следствие зависимости целевой функции I(w, u) от управления u. Такая зависимость является редкой особенностью задач оптимизации и может заметно осложнить вычисление градиента.
— следствие зависимости целевой функции I(w, u) от управления u. Такая зависимость является редкой особенностью задач оптимизации и может заметно осложнить вычисление градиента.
Значение однородного оператора 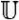 * в производной (8) имеет вид:
* в производной (8) имеет вид:
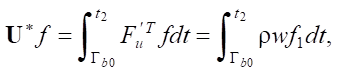
где интегрирование производится от нижней нелинейной границы Гb0 (рис. 1) при втекании воды в сопло.
Смысл и предназначение сопряженной задачи заключается в отображении производной 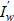 (чувствительность J к w) из области ω в область S, где определены градиент и управление. Такое отображение при помощи f делается с использованием промежуточного множества
(чувствительность J к w) из области ω в область S, где определены градиент и управление. Такое отображение при помощи f делается с использованием промежуточного множества 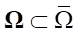 , которое, согласно управляемости, задает корректную область V*(Ω) определения однородного оператора
, которое, согласно управляемости, задает корректную область V*(Ω) определения однородного оператора 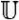 *, чтобы в выражении (8) из
*, чтобы в выражении (8) из 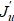 получить градиент ∇J.
получить градиент ∇J.
То есть сопряженная задача реализует отображение:
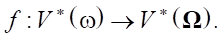
Далее при помощи оператора 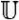 * : V*(Ω) → U*(S) можно получить градиент из производной Фреше
* : V*(Ω) → U*(S) можно получить градиент из производной Фреше 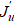 :
:
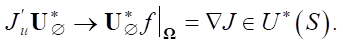
Область Ω выявляется из анализа управляемости.
Результаты исследования. Требования к условиям управляемости в рамках прямого экстремального подхода сформулированы в следующей теореме (доказательство см. в [2]).
Теорема. Математическая модель 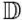 (v, u)v = 0 в задаче (3) управляема посредством u(x) на S по функционалу J если:
(v, u)v = 0 в задаче (3) управляема посредством u(x) на S по функционалу J если:
1) существует областьV*(Ω), 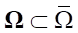 корректного сопряженного состояния, которая является областью определения оператора
корректного сопряженного состояния, которая является областью определения оператора 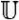 * с его значениями в области градиентов U*(S);
* с его значениями в области градиентов U*(S);
2) оператор 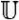 * — невырожденный;
* — невырожденный;
3) алгоритм (6) при u0∈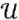 использует удовлетворительные параметры регуляризации bk.
использует удовлетворительные параметры регуляризации bk.
Начнем с первого и наиболее сложного требования теоремы. Сначала необходимо убедиться в классической корректности исходной и сопряженной задач. Исходная (3) и сопряженная (7) системы относятся к типу гиперболических. Собственные числа матриц A и AT одинаковы. Поэтому в обеих системах будут одинаковыми характеристики ξ1,2 — как траектории распространения возмущений в плоскости (x, t) вдоль характеристических направлений 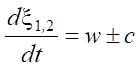 . Сопряженные волны, порождаемые производной
. Сопряженные волны, порождаемые производной 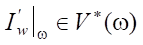 на срезе сопла Гb1 = ω, будут двигаться с теми же характеристиками, что и исходные, но в обратном направлении. Начальное условие для сопряженной задачи задано на терминальной линии Г2.
на срезе сопла Гb1 = ω, будут двигаться с теми же характеристиками, что и исходные, но в обратном направлении. Начальное условие для сопряженной задачи задано на терминальной линии Г2.
Все характеристики в области Ω выходят из участков границы 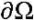 с известными решениями, заданными краевыми условиями. При течении безударных волн (именно такие течения рассматриваем в данном исследовании) характеристики одного и того же семейства не будут пересекаться, а на пересечении двух характеристик разного семейства ξ1 и ξ2 в любой точке
с известными решениями, заданными краевыми условиями. При течении безударных волн (именно такие течения рассматриваем в данном исследовании) характеристики одного и того же семейства не будут пересекаться, а на пересечении двух характеристик разного семейства ξ1 и ξ2 в любой точке 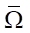 может быть найдено решение гиперболической системы двух уравнений [14] в виде двумерных вектор-функций v и f.
может быть найдено решение гиперболической системы двух уравнений [14] в виде двумерных вектор-функций v и f.
Чтобы найти область определения оператора 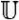 *, нужно провести анализ и выявить существование следующей последовательности отображений, начиная от управления u ∈ U(S) и заканчивая градиентом ∇J ∈ U*(S):
*, нужно провести анализ и выявить существование следующей последовательности отображений, начиная от управления u ∈ U(S) и заканчивая градиентом ∇J ∈ U*(S):
 (9)
(9)
Можно проще описать обсуждаемую проблему. Во-первых, целевой функционал J(u), заданный на ω, должен быть чувствителен к управлению, заданному на S (чувствительность характеризуется производной 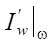 ). Во-вторых, из множества сопряженных решений на всем
). Во-вторых, из множества сопряженных решений на всем 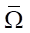 надо выделить такое подмножество Ω, где сопряженные решения
надо выделить такое подмножество Ω, где сопряженные решения 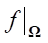 будут однозначно зависеть от значений целевого функционала в виде
будут однозначно зависеть от значений целевого функционала в виде 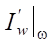 . На всей области
. На всей области 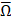 такой зависимости может и не быть. В-третьих, множество Ω должно обеспечивать оператору
такой зависимости может и не быть. В-третьих, множество Ω должно обеспечивать оператору 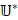 возможность отображения сопряженных состояний
возможность отображения сопряженных состояний 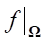 в U*(S). Такое отображение представлено последней веткой, где оператор
в U*(S). Такое отображение представлено последней веткой, где оператор 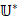 из полученной области определения V*(Ω) может произвести отображение в область значений U*(S), где существует градиент
из полученной области определения V*(Ω) может произвести отображение в область значений U*(S), где существует градиент 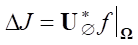 .
.
Из корректности исходной прямой задачи следует, что любые функции u(x) ∈ U(S) будут однозначно влиять на значение производной целевой функции 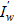 на ω = Гb1 через характеристики ξ1, если хотя бы одна из них прошла через все сопло. Потеря такого влияния возможна при наличии диссипаций в системе, но при изоэнтропических течениях этого нет. То есть имеет место левая ветка отображений в (9):
на ω = Гb1 через характеристики ξ1, если хотя бы одна из них прошла через все сопло. Потеря такого влияния возможна при наличии диссипаций в системе, но при изоэнтропических течениях этого нет. То есть имеет место левая ветка отображений в (9):
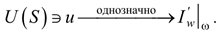
Перейдем к выявлению множества Ω, необходимого для области V*(Ω) определения оператора 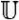 *. Член
*. Член 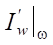 в граничном условии сопряженной задачи (7) вызывает возмущения сопряженного решения f. Они распространяются в виде волн по характеристикам первого семейства ξ1 в обратном временном направлении от среза сопла в сторону поршня (рис. 2).
в граничном условии сопряженной задачи (7) вызывает возмущения сопряженного решения f. Они распространяются в виде волн по характеристикам первого семейства ξ1 в обратном временном направлении от среза сопла в сторону поршня (рис. 2).
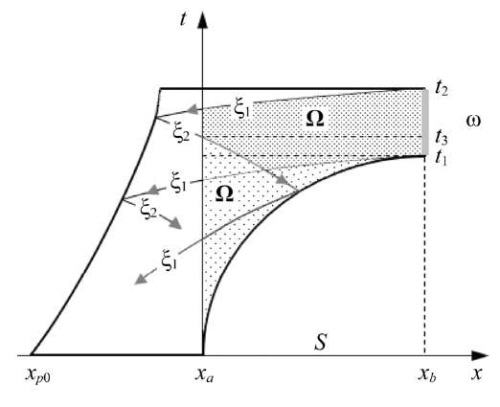
Рис. 2. Пространственно-временная диаграмма области Ω с избыточной областью ω
Эти возмущения распространяются вдоль всего сопла и переносят информацию о целевом функционале из точек ω в точки на S = (xa, xb). На поршне волны, описываемые характеристиками первого семейства ξ1, отражаются и, меняя направление своего распространения, продолжают переносить информацию, полученную от ξ1 о возмущениях 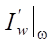 , добавляя при этом новую информацию о движении поршня. Такой процесс отражений волн от поршня и от внутренней части сопла продолжается до момента t0.
, добавляя при этом новую информацию о движении поршня. Такой процесс отражений волн от поршня и от внутренней части сопла продолжается до момента t0.
Начиная с момента t3 и ниже, в одну и ту же точку некоторых участков множества S будут приходить две сопряженные волны ξ1 и ξ2, порожденные разными значениями 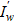 и с ненужной информацией (помехами), как минимум, от поршня. А ниже характеристики ξ1, вышедшей из сопла ниже t1, будет добавлена еще и ненужная информация от сопла. Эта информация не нужна, т. к. не содержит сведений о цели оптимизации из
и с ненужной информацией (помехами), как минимум, от поршня. А ниже характеристики ξ1, вышедшей из сопла ниже t1, будет добавлена еще и ненужная информация от сопла. Эта информация не нужна, т. к. не содержит сведений о цели оптимизации из 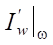 .
.
На рис. 2 показан пример возможного множества Ω (вся заштрихованная с разной плотностью область под верхней характеристикой ξ1 от xa до xb). В данном случае Ω соответствует производной Фреше 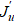 . В области Ω, под характеристикой ξ2 (отражение ξ1, вышедшей при t2) и под ξ1 (вышедшей при t1) образуется светлая область неоднозначного влияния значений функции
. В области Ω, под характеристикой ξ2 (отражение ξ1, вышедшей при t2) и под ξ1 (вышедшей при t1) образуется светлая область неоднозначного влияния значений функции 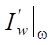 на сопряженное состояние f. Очевидно, что бессмысленно решать сопряженную задачу и рассчитывать градиент в такой области Ω.
на сопряженное состояние f. Очевидно, что бессмысленно решать сопряженную задачу и рассчитывать градиент в такой области Ω.
Разумно ограничиться рассмотрением (рис. 2) сопряженного состояния f на части Ω, заключенной в прямоугольнике:
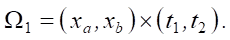
При этом прямоугольник Ω1 следует считать слишком большим, если поршень находится относительно близко к началу сопла, оказывая влияние на сопряженное состояние.
В таком прямоугольнике Ω1 множество Ω (заштриховано с разной плотностью на рис. 2 от t1 до t2) будет соответствовать избыточному множеству ω. То есть в целевом функционале J интервал (t1, t2) будет избыточным. При этом в рассматриваемой области Ω могут присутствовать неприемлемые помехи слева (малая плотность штриховки в Ω1) для вычисления градиента ∇J.
Избыточность ω устраняется дальнейшим сокращением Ω1 до t3 = t1, т. е. когда t3 соответствует началу истечения (рис. 3 а).
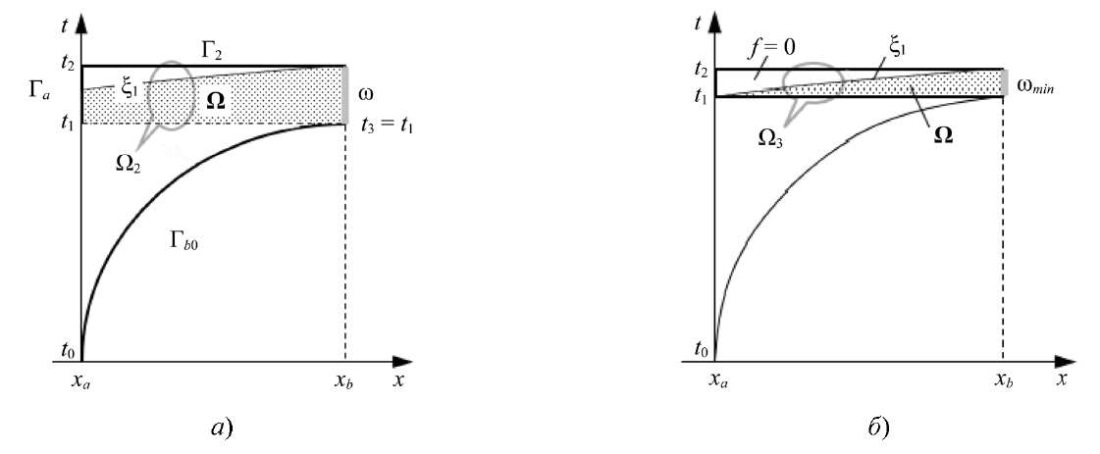
Рис. 3. Пространственно-временные диаграммы корректных областей Ω для определения градиента:
а — Ω в области Ω2; б — Ω в области Ω3
В этом случае вся область достаточного решения сопряженной задачи сужается до еще меньшего прямоугольника:
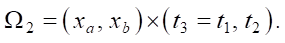
Здесь поршень не будет «мешать» отображению 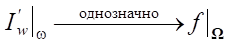 .
.
Если по техническим условиям конструирования гидропушки допускается еще большее сокращение времени истечения t2 – t1, то можно уменьшить прямоугольник решения сопряженной задачи еще сильнее, до прямоугольника Ω3 с соответствующей треугольной областью Ω (рис. 3 б):
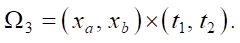
Здесь имеет место минимально достаточное множество ωmin для формирования области определения V*(Ω) оператора 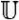 *.
*.
Именно в полученных областях Ω, находящихся внутри Ω2 и Ω3 (рис. 3), существует область определения V*(Ω) оператора 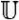 * с однозначным отображением производных
* с однозначным отображением производных 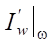 посредством f в область значений градиента U*(S).
посредством f в область значений градиента U*(S).
Сопряженная задача (7) и ее решение в прямоугольниках Ω2,3 становятся существенно проще:
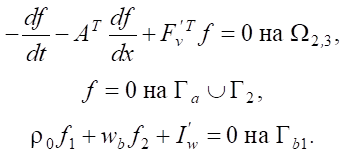 (10)
(10)
Здесь Гa = xa × (t1, t2). Теперь нет влияния поршня с линии 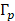 и нет втекания в сопло на границе Гb0.
и нет втекания в сопло на границе Гb0.
Формула (8) расчета градиента целевого функционала также принимает упрощенный вид (нет нелинейной границы интегрирования Гb0):
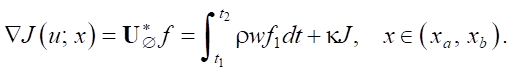 (11)
(11)
Полученное множество Ω ⊂ Ω2,3 будет корректно задавать область V*(Ω) определения оператора 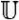 *(Ω) с областью значений в U*(S). Соответствующее выражение времени, необходимое для формирования такого Ω, зависит от характеристик первого семейства ξ1 и имеет вид:
*(Ω) с областью значений в U*(S). Соответствующее выражение времени, необходимое для формирования такого Ω, зависит от характеристик первого семейства ξ1 и имеет вид:
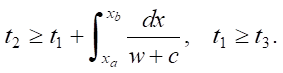 (12)
(12)
То есть, во-первых, верхняя характеристика ξ1 должна пройти через всё сопло от xb до xa, во-вторых, начало истечения t1 не должно быть меньше момента t3 начала попадания в сопло волн, отражённых от поршня.
Данное выражение является условием управляемости в рассматриваемой задаче. При этом выполняются оставшиеся ветки отображений (9):
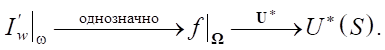
Теперь обсудим требование 2 в теореме о невырожденности оператора 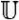 *. Начнем с оператора
*. Начнем с оператора 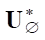 , задающего градиент (8). Если бы целевая функция I не зависела явно от управления u, то
, задающего градиент (8). Если бы целевая функция I не зависела явно от управления u, то 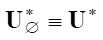 и множество сопряженных состояний в ядре fker = {f :
и множество сопряженных состояний в ядре fker = {f : 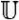 *f = 0 на S} было бы нулевым при неограниченном оптимальном управлении u*. В нашем же случае для
*f = 0 на S} было бы нулевым при неограниченном оптимальном управлении u*. В нашем же случае для 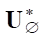 значения элементов ядра fker не будут нулевыми, т. е. оптимальному управлению будут соответствовать ненулевые сопряженные состояния. Нижний индекс
значения элементов ядра fker не будут нулевыми, т. е. оптимальному управлению будут соответствовать ненулевые сопряженные состояния. Нижний индекс 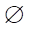 означает отсутствие нулевого ядра. Очевидно, что если
означает отсутствие нулевого ядра. Очевидно, что если 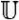 * был невырожденным, то и оператор
* был невырожденным, то и оператор 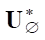 будет невырожденным. Неоднородность оператора
будет невырожденным. Неоднородность оператора 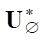 в нашей задаче приводит всего лишь к смещению нулевого ядра однородного оператора
в нашей задаче приводит всего лишь к смещению нулевого ядра однородного оператора 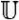 *.
*.
Оценим возможную вырожденность однородного оператора 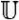 *. Очевидно, что при любых значениях ρ и w результат интегрирования в
*. Очевидно, что при любых значениях ρ и w результат интегрирования в 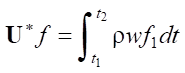 может стать нулевым на S только при f1 = 0 на Ω. Это означает, что оператор
может стать нулевым на S только при f1 = 0 на Ω. Это означает, что оператор 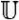 * — невырожденный, а следовательно, и
* — невырожденный, а следовательно, и 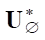 — невырожденный.
— невырожденный.
Остается последнее требование теоремы. Регуляризация в прямом экстремальном подходе обеспечивается:
- выбором начального приближения u0∈
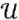 ;
; - последующими шагами алгоритмов типа (6) с удовлетворительным параметром регуляризации, т. е. с параметром bk, не выводящим управление uk+1 за пределы компакта
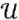 .
.
В работе [8] описаны необходимые регуляризирующие градиентные методы для алгоритма (6) в рассматриваемой задаче.
Таким образом, все требования теоремы для обеспечения управляемости выполнены. Распределенная система (3) управляема посредством u(x) на S по функционалу J (5) при условии (12).
Результаты использования условий управляемости для гидропушки. Параметры экспериментальной установки были заимствованы из исследования А. Н. Семко [15]:
- начало координат xa=0;
- длина сопла xb=0,253 м;
- начальное положение поршня с левой границей воды xp0=–0,28 м;
- масса поршня mp=2,25 кг;
- начальная скорость поршня и воды ω0= 76,2 м/с;
- плотность воды при атмосферном давлении ρ0= 103 кг/м3;
- радиус ствола гидропушки Ra=33 ∙ 10–3 м;
- начало втекания воды в сопло t0=0.
Исходная задача решалась в сложной замкнутой области 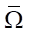 , а сопряженная — на небольшом прямоугольнике
, а сопряженная — на небольшом прямоугольнике 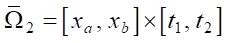 . Были построены две пространственные сетки, каждая из которых содержит 50 шагов. Первая сетка является подвижной и используется для расчета течения воды от поршня до среза сопла, тогда как вторая сетка неподвижна и предназначена для описания формы сопла. Количество слоев по времени было переменным и доходило до 103. Точное значение зависит от формы сопла и определяется конечным временем t2. Исходная и сопряженная задачи решалась методом характеристик на одинаковых подвижных сетках в
. Были построены две пространственные сетки, каждая из которых содержит 50 шагов. Первая сетка является подвижной и используется для расчета течения воды от поршня до среза сопла, тогда как вторая сетка неподвижна и предназначена для описания формы сопла. Количество слоев по времени было переменным и доходило до 103. Точное значение зависит от формы сопла и определяется конечным временем t2. Исходная и сопряженная задачи решалась методом характеристик на одинаковых подвижных сетках в 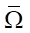 и в
и в 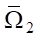 соответственно.
соответственно.
Начало истечения струи из сопла наблюдалось при t1 ≈ 2,7 ∙ 10–3 с.
Среднее значение силы импульса полученной струи оценивалось по целевому функционалу J(u) в интервале t2 – t1 = 3 ∙ 10–4 c.
Данный интервал составляет примерно 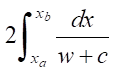 . При этом время начала истечения t1 > t3, т. е. поршень не влияет на истечение. Таким образом, заданное время t2 удовлетворяет условию управляемости (12).
. При этом время начала истечения t1 > t3, т. е. поршень не влияет на истечение. Таким образом, заданное время t2 удовлетворяет условию управляемости (12).
В работе [8] реализованы необходимые адаптивные вычислительные экстремальные алгоритмы с учетом описанных здесь условий управляемости и приведены впервые полученные оптимальные формы сопла.
На рис. 4 сопло 1 соответствует внутреннему локальному максимуму функционала J(u), а сопло 2 — краевому максимуму при ограничении на расширение сопла: u(x) ≤ 0, ∀x ∈ S. Первое сопло практически имеет форму конуса, в то время как второе обеспечивает целевому функционалу достижение глобального максимума, значение которого J примерно в три раза превышает значение, полученное для первого сопла.
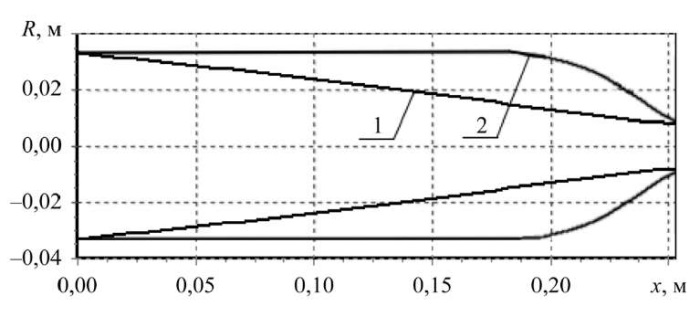
Рис. 4. Оптимальные формы сопла гидропушки
Начальное приближение u0(x) задавалось в виде трубы — как продолжение ствола пушки. На первых итерациях сужения сопла рост функционала J(u) происходил при его выпуклости (рост нормы ∇J). Далее выпуклость сменилась на вогнутость (убывание нормы ∇J), в конце которой находились очень малые области максимума (минимальная норма ∇J при вогнутости функционала) с последующим выпуклым минимумом. В локальном максимуме было получено сопло 1. Переход через эти локальные экстремумы сопровождался далее неограниченным выпуклым ростом J(u). Только добавление ограничения на управление позволило остановить неконтролируемое расширение сопла на границе с разумной формой 2.
Напомним, что ранее предпринимались попытки получить удовлетворительное решение с помощью классического вариационного исчисления. Для этого авторы работ [5] и [7] задействовали методы релаксации для поиска корня u* из необходимого условия оптимальности 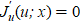 (производная Фреше
(производная Фреше 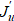 на некорректном Ω из рис. 2). Однако такой подход не дал желаемых результатов. Более того, он требует дополнительного ограничения на площадь среза сопла для предотвращения его схлопывания. Такое схлопывание также подтверждает некорректность использования
на некорректном Ω из рис. 2). Однако такой подход не дал желаемых результатов. Более того, он требует дополнительного ограничения на площадь среза сопла для предотвращения его схлопывания. Такое схлопывание также подтверждает некорректность использования 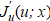 для направленного поиска u*(x) без выделения области управляемости Ω внутри Ω2,3. Иными словами, вместо производной Фреше необходимо получить градиент с обоснованием.
для направленного поиска u*(x) без выделения области управляемости Ω внутри Ω2,3. Иными словами, вместо производной Фреше необходимо получить градиент с обоснованием.
Обсуждение и заключение. Результаты исследования демонстрируют, что применение анализа управляемости, предложенного в работе [2], позволило выявить ключевые условия управляемости (12), необходимые для корректной постановки и решения задачи оптимизации формы сопла гидропушки.
Согласно условиям управляемости, задачу оптимизации необходимо ставить и решать в малой прямоугольной области Ω2 или даже Ω3, а не в большой и сложной области Ω. Это связано с тем, что задача оптимизации формы сопла с постановкой в Ω не приводит производную Фреше 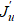 к градиенту ∇J, что делает невозможным направленный поиск оптимального решения. Именно это обстоятельство стало причиной неудач предыдущих исследований, где оптимальность решений не была доказана.
к градиенту ∇J, что делает невозможным направленный поиск оптимального решения. Именно это обстоятельство стало причиной неудач предыдущих исследований, где оптимальность решений не была доказана.
Рекомендуем сначала делать анализ управляемости до выявления корректной области управляемости Ω, а потом для полученной Ω выделять область решения сопряженной задачи (в нашем случае — это Ω2 или Ω3) и находить вариацию 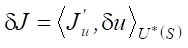 . Затем можно продолжить анализ управляемости и из производной
. Затем можно продолжить анализ управляемости и из производной 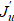 получить градиент ∇J. Именно с помощью Ω внутри Ω2,3 можно найти значение градиента ∇J(u; x), которое распределено вдоль всего сопла и однозначно соответствует целевому функционалу задачи J(u). Далее можно целенаправленно искать оптимальную форму сопла.
получить градиент ∇J. Именно с помощью Ω внутри Ω2,3 можно найти значение градиента ∇J(u; x), которое распределено вдоль всего сопла и однозначно соответствует целевому функционалу задачи J(u). Далее можно целенаправленно искать оптимальную форму сопла.
Основное преимущество предложенного подхода заключается в использовании прямого экстремального метода, который позволяет непосредственно максимизировать целевой функционал с помощью градиентных алгоритмов. Это обеспечивает не только наглядность анализа управляемости, но и возможность получения численно подтвержденных оптимальных решений.
Теоретическая ценность исследования состоит в развитии методов анализа управляемости для систем с распределенными параметрами, что открывает новые перспективы для решения аналогичных задач в других областях. Дальнейшие исследования могут быть направлены на расширение метода для более сложных моделей течения жидкости, а также на оптимизацию других устройств, работающих на основе импульсных струй.
Список литературы
1. Егоров А.И., Знаменская Л.Н. Введение в теорию управления системами с распределенными параметрами. СПб: Лань; 2022. 292 с. URL: https://e.lanbook.com/book/167413 (дата обращения: 10.11.2024).
2. Tolstykh VK. Controllability of Distributed Parameter Systems. Computational Mathematics and Mathematical Physics. 2024;64(6):1211–1223. https://doi.org/10.1134/S0965542524700453
3. Мерзляков В.Г., Деревяшкин И.В., Бойкова И.Е., Толмачев А.И. Разрушение угля и горных пород высокоскоростными струями воды. Горный информационно-аналитический бюллетень. 2023;(4):140–156. URL: https://giab-online.ru/files/Data/2023/4/04_2023_140-156.pdf (дата обращения: 10.11.2024).
4. Очеретяный С.А., Прокофьев В.В. Влияние параметров кавитатора и сопла на эффективность работы генератора импульсных струй. Известия РАН. Механика жидкости и газа. 2023;(5):10–24. https://doi.org/10.31857/S1024708422600981
5. Зуйкова З.Г. Вариационная задача о втекании сжимаемой жидкости в сужающийся канал. Дис. канд. физ.-мат. наук. Донецк: ДонГУ; 1984. 84 с.
6. Зубов В.И., Зуйкова З.Г. Об одном классе решений задачи оптимизации сопла гидропушки. Журнал вычислительной математики и математической физики. 1994;34(10):1541–1550. URL: https://www.mathnet.ru/links/ef53959cbfdf54e2c020c950fae97778/zvmmf2511.pdf (дата обращения: 10.11.2024).
7. Atanov GA. The Optimal Control Problem of Profiling the Hydro-Cannon Nozzle to Obtain the Maximum Outlet Speed. Proceedings of the Institution of Mechanical Engineers, Part C. 1997;211(7):541–547.
8. Tolstykh VK. Algorithms for Optimizing Systems with Multiple Extremum Functionals. Computational Mathematics and Mathematical Physics. 2024;64(3):392–400. https://doi.org/10.1134/S0965542524030163
9. Кабанихин С.И. Обратные задачи естествознания. Журнал вычислительной математики и математической физики. 2020;60(6):935–938. https://doi.org/10.31857/S0044466920060046
10. Артемьева Л.А., Дряженков А.А., Потапов М.М. Устойчивое решение задачи квадратичной минимизации с неравномерно возмущенным оператором регуляризованным градиентным методом. Журнал вычислительной математики и математической физики. 2022;62(1):12–22. https://doi.org/10.31857/S0044466922010033
11. Семко А.Н., Локтюшина Ю.В. Об учёте сжимаемости жидкости при расчёте течения в гидропушке. Вестник Донецкого национального университета. 2011;(2):95–101. URL: https://donnu.ru/public/journals/files/Vestnik_DonNU_2011_N2_compr.pdf#page=96 (дата обращения: 10.11.2024).
12. Гусев А.А. Основы гидравлики, 3-е изд., испр. и доп. Москва: Юрайт, 2019. 218 с. https://urait.ru/index.php/bcode/423733
13. Корпусов М.О., Панин А.А. Лекции по линейному и нелинейному функциональному анализу. Том III. Нелинейный анализ. Москва: Московский государственный университет имени М.В. Ломоносова; 2016. 235 с.
14. Емельянов В.Н. Численные методы: введение в теорию разностных схем. Москва: Юрайт; 2023. 188 с. https://urait.ru/bcode/562837 (дата обращения: 10.11.2024).
15. Семко А.Н. Импульсные струи жидкости высокой скорости и их применение. Донецк: Донецкий национальный университет; 2014. 370 с.
Об авторах
В. К. ТолстыхРоссия
Виктор Константинович Толстых, доктор физико-математических наук, доктор технических наук, профессор кафедры компьютерных технологий
Scopus ID: 6701477776
Researcher ID: JPV-1128-2023
283001, Донецкая Народная Республика, г. Донецк, ул. Университетская, д. 24
Ю. В. Дмитрук
Россия
Юлия Владимировна Дмитрук, старший преподаватель кафедры общей физики и дидактики физики
283001, Донецкая Народная Республика, г. Донецк, ул. Университетская, д. 24
Рецензия
Для цитирования:
Толстых В.К., Дмитрук Ю.В. Анализ управляемости и оптимизация формы сопла гидропушки на основе прямого экстремального подхода. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):65-76. https://doi.org/10.23947/2687-1653-2025-25-1-65-76. EDN: RVWIZA
For citation:
Tolstykh V.K., Dmitruk Yu.V. Controllability Analysis and Optimization of Hydrocannon Nozzle Shape Based on Direct Extreme Approach. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):65-76. https://doi.org/10.23947/2687-1653-2025-25-1-65-76. EDN: RVWIZA
JATS XML














































