Scroll to:
Controllability Analysis and Optimization of Hydrocannon Nozzle Shape Based on Direct Extreme Approach
https://doi.org/10.23947/2687-1653-2025-25-1-65-76
EDN: RVWIZA
Abstract
Introduction. Controllability analysis is a required stage for the correct formulation and solution of any optimal control problem. This problem becomes specifically relevant in the context of optimizing systems with distributed parameters, which are described by partial difference equations. Such problems include the considered problem of optimization of the shape of the nozzle of a hydrocannon. The optimal nozzle should provide the maximum value of the functional expressed through the average force of the impulse of the jet of a hydrocannon. The relevance of this research is due to the lack of a unified approach to the analysis of controllability of systems with distributed parameters, which complicates the correct formulation and solution of optimization problems. In particular, previous attempts to solve the problem of hydrocannon nozzle optimization using classical variational calculus were unsuccessful due to ignoring aspects of controllability. The objective of this research was to apply a new approach proposed by V.K. Tolstykh to controllability analysis to solve the problem of optimal design of the shape of a hydrocannon nozzle.
Materials and Methods. The research method used was controllability analysis based on the Tikhonov conditional correctness of the inverse problem. This approach allowed us to identify the conditions for the existence of the gradient of the objective functional and construct a regularization of the solution to the inverse problem using adaptive gradient methods. It was of current interest for multiextremal problems, including the problem of the optimum nozzle shape. It was solved by a direct extreme approach in the form of direct maximization of the objective functional based on its gradient. In the process of research, a nonlinear, quasi-one-dimensional mathematical model of isentropic water flow in a hydrocannon nozzle was used. The flow was considered inviscid, compressible, and subsonic.
Results. As part of the research, controllability conditions were obtained that allowed us to radically simplify the problem of optimizing the shape of the hydrocannon nozzle. It was found that in order to correctly determine the gradient of the objective functional, it was required to narrow the solution area of the conjugate problem to a small rectangular area. The use of adaptive gradient methods with satisfactory step factors provided for the regularization of the solution. For the first time, two optimum shapes of the hydrocannon nozzle were found. The first shape provided a local maximum of the objective functional, the second — a global maximum of the functional with a restriction on the expansion of the nozzle.
Discussion and Conclusion. The results obtained show that it is impossible to perform a directed search for an optimal solution using the Frechet derivative without taking into account controllability conditions. The first proposed approach, in combination with the desired adaptive gradient optimization methods, allowed us not only to correctly formulate the optimization problem, but also to find optimal nozzle shapes that provided the maximum average pulse force of the ultrajet. In some cases, for the stability of the solution, it was necessary to introduce expansion limitation of the nozzle beyond the barrel of the hydrocannon. This made it possible to meet the requirements of the controllability theorem and guaranteed the correctness of the results obtained. The theoretical relevance of the research is in the development of controllability analysis methods for systems with distributed parameters, which creates new opportunities for solving similar problems in other areas. The research results can be used to optimize devices operating on the basis of pulsed jets, as well as for further study of more complex models of fluid flow.
Keywords
For citations:
Tolstykh V.K., Dmitruk Yu.V. Controllability Analysis and Optimization of Hydrocannon Nozzle Shape Based on Direct Extreme Approach. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):65-76. https://doi.org/10.23947/2687-1653-2025-25-1-65-76. EDN: RVWIZA
Introduction. Despite the significant amount of research on the control theory, there is still no unified approach to the analysis of controllability for systems with distributed parameters. Existing studies are usually limited to considering controllability as the possibility of transferring a system from an initial state to a given final state [1]. However, this approach turns out to be insufficient for optimization problems of spatially distributed systems described by partial differential equations. Controllability by the final state does not guarantee controllability by the conditions specified in the objective functional, which makes the analysis of such systems complex and non-obvious. In this paper, the authors use the concept of controllability proposed by V.K. Tolstykh [2] and apply it to find the optimal shape of the hydrocannon nozzle.
Hydraulic cannons designed to generate pulsed jets of high-pressure liquid are widely used, e.g., in the mining industry to destroy rocks [3]. The efficiency of such devices largely depends on the shape of the nozzle [4], which makes the task of its optimization urgent. Despite significant interest in this problem, existing papers, such as the works of Zuikova Z.G. [5], Zubov V.I. [6], and Atanova G.A. [7], are primarily theoretical. These authors formulated the required conditions for optimality, but the numerical results were not supported by evidence of their optimality. Moreover, as it is shown in this research, the previously obtained “optimal” nozzle shapes are not such. Thus, despite multi-year research, the problem of designing an optimal nozzle shape remains unsolved.
The solution to this complex problem is possible only through using a direct extreme approach with original adaptive gradient methods described in the work of V.K. Tolstykh [8]. The objective of this work was to apply the new approach proposed in [2] to the analysis of the controllability of a system with distributed parameters for the problem of optimal design of the hydrocannon nozzle shape. Thus, the article is aimed at developing the controllability theory for systems with distributed parameters and demonstrating its practical applicability using the example of optimizing the shape of a hydrocannon nozzle.
Materials and Methods. The essence of the direct extreme approach is the direct maximization of some objective functional using gradient methods:
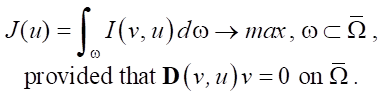 , (1)
, (1)
Here, the control (in our case — function of the nozzle shape along the length x) u(x) ∈ U(S), S = (xa, xb) — domain of control definition, U — admissible set of controls, v(x, t) ∈ V(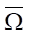 ) — state of the nonstationary process of ultra-jet formation on the closed space-time set {x, t} =
) — state of the nonstationary process of ultra-jet formation on the closed space-time set {x, t} = 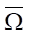 . Operator
. Operator 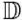 includes a specific type of differential equations of water flow in a hydrocannon and acts on v. Objective function I(v, u) is defined on the set ω, and its value clearly depends on the parameters v and u.
includes a specific type of differential equations of water flow in a hydrocannon and acts on v. Objective function I(v, u) is defined on the set ω, and its value clearly depends on the parameters v and u.
The direct approach does not use any intermediate conditions (e.g., required optimality conditions), but solves the problem immediately:
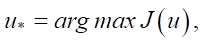 (2)
(2)
where u* — optimal control.
The original problem with the equations of the distributed system (v, u)v = 0 is characterized by a direct mapping:
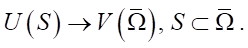
At the same time, optimization problem (1) is inverse. Such problems are usually ill-posed in the classical sense [9]. The solution to direct and inverse problems differs significantly. The latter require regularization of the solution to narrow the set of possible solutions U to the compact of correctness  ⊆ U, which leads to conditional correctness according to Tikhonov. In the direct extreme approach, regularization is performed by gradient methods.
⊆ U, which leads to conditional correctness according to Tikhonov. In the direct extreme approach, regularization is performed by gradient methods.
According to the definition of controllability [2], the distributed system in problem (1) will be controllable by u(x) ∈ U(S) with respect to objective functional J, when the inverse problem of mapping the elements of space V(ω) of model states into element u* is correct according to Tikhonov, provided that max J:
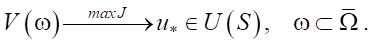
Next, when solving problem (2), we will perform a controllability analysis and obtain controllability conditions that can allow us to correctly formulate and solve the problem of optimizing the shape of the hydrocannon nozzle using gradient methods [10].
Paper [8] describes in detail the formulation of the problem under consideration for subsonic, axisymmetric flows of compressible fluid in smoothly changing channels. Let us recall it in the form required for further research. The isentropic motion of water in the nozzle is described by a quasi-one-dimensional, quasi-linear hyperbolic system of equations [11]:
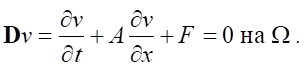 (3)
(3)
The state of the system is characterized by vector function v = {ρ, w} ∈ V( ), where ρ — density of water, w — speed of water. Operator
), where ρ — density of water, w — speed of water. Operator 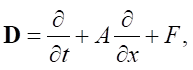 its matrix
its matrix 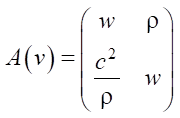 and vector
and vector 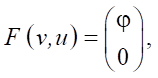 φ = ρwuΘ(x – xa), Θ — Dirac theta function, xa — beginning of the nozzle at the end of the barrel of hydrocannon,
φ = ρwuΘ(x – xa), Θ — Dirac theta function, xa — beginning of the nozzle at the end of the barrel of hydrocannon, 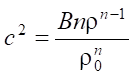 — square of the speed of sound in water, B and n — constants in the equation of state of water in theta form.
— square of the speed of sound in water, B and n — constants in the equation of state of water in theta form.
The control is described by the formula:
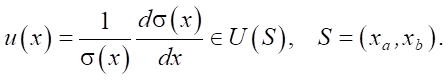 (4)
(4)
Here, σ — nozzle cross-sectional area, 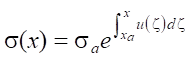 , x ∈ [xa, xb], σa = σ(xa). In the barrel of the hydrocannon, when x ≤ xa, there is no control u(x), and free term φ = 0.
, x ∈ [xa, xb], σa = σ(xa). In the barrel of the hydrocannon, when x ≤ xa, there is no control u(x), and free term φ = 0.
Boundary and initial conditions of problem (3):
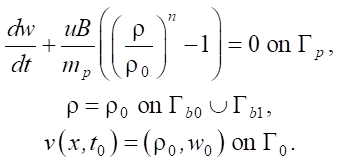
Here, mp — piston mass, ρ0 — density of water at atmospheric pressure, w0 — speed of water and piston before it starts flowing into the nozzle. The boundaries of process Г for domain Ω, are shown in Figure 1. The type of Ω is important for the controllability analysis.
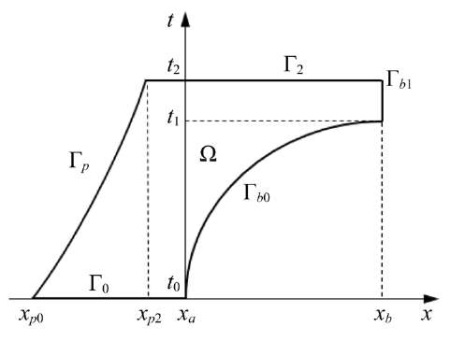
Fig. 1. Area of water flow in the hydrocannon
We specify Ω. The origin of coordinates is aligned with the nozzle entrance xa, and t0 — time of the beginning of water flow into the nozzle. On the one hand, the water is limited by the piston moving in the barrel of the hydrocannon along the trajectory Гp, and on the other hand — by the free surface of the inflow Гb0 from t0 to t1 and the outflow Гb1 from t1 to t2. The line of the initial state of system (3) is Г0, coordinates xp0 and xp2 — initial and final positions of the piston. The specified Г-lines for Ω form the closure of 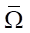 . The domain of definition of the control
. The domain of definition of the control 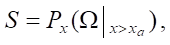 i.e., for x > xa, S is the projection of a part of domain Ω onto x axis.
i.e., for x > xa, S is the projection of a part of domain Ω onto x axis.
The optimization problem (optimal design of the nozzle shape) is formulated as follows: it is necessary to find the control u(x) that delivers the maximum to the functional:
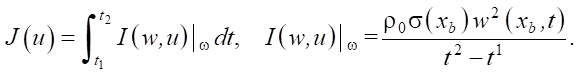 (5)
(5)
The objective functional is set at ω = Гb1, i.e., at the nozzle exit of the hydrocannon, and determines the average force of the jet on a possible obstacle [12].
The gradient algorithm for maximizing functional (5) has the form:
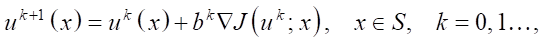 (6)
(6)
where k — iteration number; bk — step multiplier that controls the rise to max J in the direction of gradient ∇Jk.
The gradient is the functional Frechet derivative 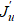 , which can be found from the first variation of the objective functional
, which can be found from the first variation of the objective functional 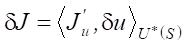 . Here, the angle brackets denote the scalar product, in this case, in the conjugate control space U*(S). The superscript * denotes conjugacy.
. Here, the angle brackets denote the scalar product, in this case, in the conjugate control space U*(S). The superscript * denotes conjugacy.
It should be noted that sometimes the gradient of a functional on a Hilbert space is confused with the Frechet derivative of this functional [13]. Derivative 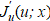 may be insensitive to the control u(x) on the entire set S or on parts of S of nonzero measure. Therefore, in the general case, in (6) will not indicate a reliable direction of correction uk for the directed search for the optimal solution
may be insensitive to the control u(x) on the entire set S or on parts of S of nonzero measure. Therefore, in the general case, in (6) will not indicate a reliable direction of correction uk for the directed search for the optimal solution 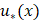 The gradient from the Frechet derivative can be obtained only when the controllability conditions are realized.
The gradient from the Frechet derivative can be obtained only when the controllability conditions are realized.
Approaches to solving problems of hydrocannon nozzle optimization with the aim of maximizing the average jet impulse force [5], the functional depending on the flow parameters [6], and maximizing the outflow velocity [7] were mentioned earlier. In these papers, after varying δJ, a formal expression for derivative 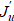 was obtained. It depends on the solution
was obtained. It depends on the solution 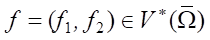 of the linear conjugate hyperbolic problem:
of the linear conjugate hyperbolic problem:
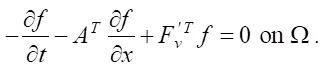 (7)
(7)
The superscript T means transposition, 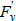 — deriva F tive of the free term F with respect to v. Boundary and initial (terminal on Г2) conditions:
— deriva F tive of the free term F with respect to v. Boundary and initial (terminal on Г2) conditions:
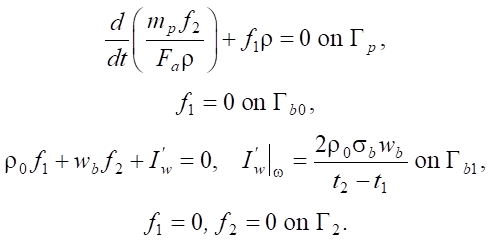
Frechet derivative 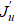 is sometimes called the residual or gradient. It is more convenient to represent it in operator form:
is sometimes called the residual or gradient. It is more convenient to represent it in operator form:
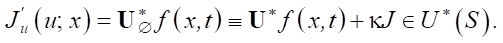 (8)
(8)
Here, the conjugate inhomogeneous operator 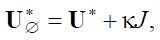
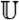 *— conjugate homogeneous operator, the dot denotes the location of argument f of the operators, κ — weight coefficient for equalizing the computational noise of the numerical solution of the original and conjugate problems [8]. Expression (8) contains the value of the functional in the form of the number J. This is the value of derivative
*— conjugate homogeneous operator, the dot denotes the location of argument f of the operators, κ — weight coefficient for equalizing the computational noise of the numerical solution of the original and conjugate problems [8]. Expression (8) contains the value of the functional in the form of the number J. This is the value of derivative 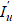 .
.
The heterogeneity of operator 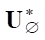 is a consequence of the dependence of the objective function I(w, u) on the control u. Such a dependence is a rare feature of optimization problems and can significantly complicate the calculation of the gradient.
is a consequence of the dependence of the objective function I(w, u) on the control u. Such a dependence is a rare feature of optimization problems and can significantly complicate the calculation of the gradient.
The value of homogeneous operator 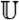 * in derivative (8) has the form:
* in derivative (8) has the form:
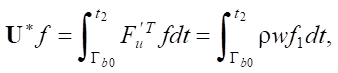
where integration is performed from the lower nonlinear boundary Гb0 (Fig. 1) when water flows into the nozzle.
The meaning and objective of the conjugate problem is to map derivative 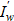 (sensitivity of J to w) from domain ω to domain S, where the gradient and control are defined. Such a mapping with the help of f is done using the intermediate set
(sensitivity of J to w) from domain ω to domain S, where the gradient and control are defined. Such a mapping with the help of f is done using the intermediate set  which, according to controllability, specifies the correct domain V*(Ω) of the definition of the homogeneous operator
which, according to controllability, specifies the correct domain V*(Ω) of the definition of the homogeneous operator 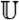 *, so that in expression (8) from
*, so that in expression (8) from  , we obtain gradient ∇J.
, we obtain gradient ∇J.
That is, the conjugate problem implements the mapping:
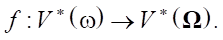
Next, using operator 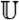 * : V*(Ω) → U*(S), we can obtain the gradient from Frechet derivative
* : V*(Ω) → U*(S), we can obtain the gradient from Frechet derivative 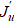 :
:
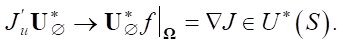
Domain Ω is determined from the controllability analysis.
Research Results. The requirements for controllability conditions within the framework of the direct extreme approach are formulated in the following theorem (for the proof, see [2]).
Theorem. The mathematical model (v, u)v = 0 in problem (3) is controllable by u(x) on S with respect to functional J if:
1) there exists domain V*(Ω), 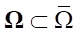 of a correct conjugate state, which is the domain of definition of operator
of a correct conjugate state, which is the domain of definition of operator 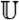 * with its values in the gradient domain U*(S);
* with its values in the gradient domain U*(S);
2) operator 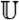 * — non-degenerate;
* — non-degenerate;
3) algorithm (6) for u0∈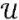 uses satisfactory regularization parameters bk.
uses satisfactory regularization parameters bk.
We start with the first and most difficult requirement of the theorem. First, it is necessary to verify the classical correctness of the original and conjugate problems. Original (3) and conjugate (7) systems are of the hyperbolic type. The eigenvalues of the matrices A and AT are the same. Therefore, in both systems, the characteristics ξ1,2 will be the same — as the trajectories of the propagation of disturbances in the plane (x, t) along the characteristic directions 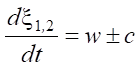 . The conjugate waves generated by derivative
. The conjugate waves generated by derivative 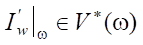 at the nozzle exit Гb1 = ω, will move with the same characteristics as the original ones, but in the opposite direction. The initial condition for the conjugate problem is specified on the terminal line Г2.
at the nozzle exit Гb1 = ω, will move with the same characteristics as the original ones, but in the opposite direction. The initial condition for the conjugate problem is specified on the terminal line Г2.
All characteristics in domain Ω emerge from the boundary sections 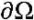 with known solutions given by the boundary conditions. In the case of shock-free wave flows (it is precisely such flows that are considered in this research), the characteristics of the same family do not intersect, and at the intersection of two characteristics of a different family ξ1 and ξ2 at any point
with known solutions given by the boundary conditions. In the case of shock-free wave flows (it is precisely such flows that are considered in this research), the characteristics of the same family do not intersect, and at the intersection of two characteristics of a different family ξ1 and ξ2 at any point 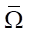 , a solution to the hyperbolic system of two equations [14] can be found in the form of two-dimensional vector functions v and f.
, a solution to the hyperbolic system of two equations [14] can be found in the form of two-dimensional vector functions v and f.
To find the domain of operator 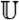 *, it is necessary to conduct an analysis and identify the existence of the following sequence of mappings, starting from the control u ∈ U(S) and ending with gradient ∇J ∈ U*(S):
*, it is necessary to conduct an analysis and identify the existence of the following sequence of mappings, starting from the control u ∈ U(S) and ending with gradient ∇J ∈ U*(S):
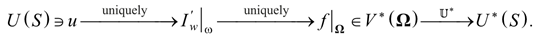 (9)
(9)
The problem under discussion can be described more simply. First, objective functional J(u), specified on ω, must be sensitive to the control defined on S (sensitivity is characterized by derivative 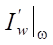 ). Second, from the set of conjugate solutions on the entire
). Second, from the set of conjugate solutions on the entire 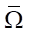 , it is necessary to select such a subset Ω, where the conjugate solutions
, it is necessary to select such a subset Ω, where the conjugate solutions 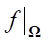 will uniquely depend on the values of the objective functional in the form
will uniquely depend on the values of the objective functional in the form 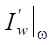 . There may not be such a dependence on the entire domain
. There may not be such a dependence on the entire domain 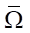 . Thirdly, the set Ω must provide operator
. Thirdly, the set Ω must provide operator 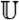 * with the ability to map the conjugate states
* with the ability to map the conjugate states 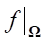 into U*(S). This mapping is represented by the last branch, where operator
into U*(S). This mapping is represented by the last branch, where operator 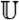 * from the obtained domain of definition
* from the obtained domain of definition 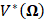 can produce a mapping into the domain of values U*(S). where there is gradient
can produce a mapping into the domain of values U*(S). where there is gradient 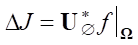 .
.
From the correctness of the original direct problem, it follows that any functions u(x) ∈ U(S) will uniquely affect the value of the derivative of the objective function 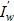 on ω = Гb1 through the characteristics ξ1, if at least one of them has passed through the entire nozzle. The loss of such effect is possible in the presence of dissipation in the system, but this is not the case with isentropic flows. That is, there is a left branch of mappings in (9):
on ω = Гb1 through the characteristics ξ1, if at least one of them has passed through the entire nozzle. The loss of such effect is possible in the presence of dissipation in the system, but this is not the case with isentropic flows. That is, there is a left branch of mappings in (9):

Let us proceed to identifying the set Ω, required for domain V*(Ω) of the definition of operator 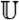 *. Term
*. Term 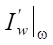 in the boundary condition of conjugate problem (7) causes perturbations of the conjugate solution f. They propagate in the form of waves along the characteristics of the first family ξ1 in the reverse time direction from the nozzle exit toward the piston (Fig. 2).
in the boundary condition of conjugate problem (7) causes perturbations of the conjugate solution f. They propagate in the form of waves along the characteristics of the first family ξ1 in the reverse time direction from the nozzle exit toward the piston (Fig. 2).
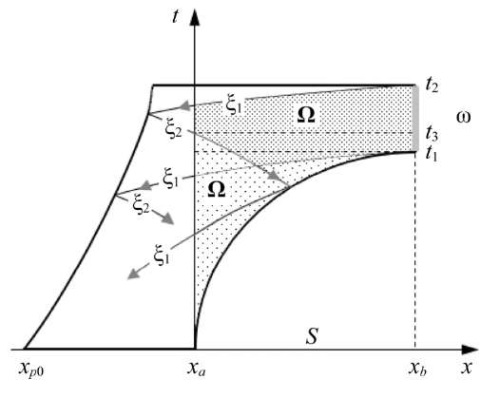
Fig. 2. Space-time diagram of domain Ω with redundant domain ω
These disturbances propagate along the entire nozzle and transfer information about the objective functional from the points 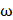 to the points on S = (xa, xb). On the piston, the waves described by the characteristics of the first family ξ1, are reflected and, changing the direction of their propagation, continue to transfer information received from ξ1 about disturbances
to the points on S = (xa, xb). On the piston, the waves described by the characteristics of the first family ξ1, are reflected and, changing the direction of their propagation, continue to transfer information received from ξ1 about disturbances 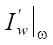 , adding new information about the piston motion. This process of wave reflections from the piston and from the inner part of the nozzle continues until the moment t0.
, adding new information about the piston motion. This process of wave reflections from the piston and from the inner part of the nozzle continues until the moment t0.
Starting from the moment t3 and below, two conjugate waves ξ1 and ξ2, generated by different values of 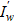 and with unnecessary information (noise), at a minimum, will arrive at the same point of some sections of the set S from the piston. And below the characteristic ξ1, which came out of the nozzle below t1, unnecessary information from the nozzle will be added. This information is not needed, since it does not contain information about the optimization goal from
and with unnecessary information (noise), at a minimum, will arrive at the same point of some sections of the set S from the piston. And below the characteristic ξ1, which came out of the nozzle below t1, unnecessary information from the nozzle will be added. This information is not needed, since it does not contain information about the optimization goal from 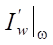 .
.
Figure 2 shows an example of a possible set Ω (the entire area shaded with different densities under the upper characteristic ξ1 from xa to xb). In this case, Ω corresponds to the Frechet derivative  . In domain Ω, under characteristic ξ2 (reflection ξ1, which came out at t2) and under ξ1 (which came out at t1), a light area of ambiguous influence of the values of function
. In domain Ω, under characteristic ξ2 (reflection ξ1, which came out at t2) and under ξ1 (which came out at t1), a light area of ambiguous influence of the values of function 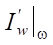 on the conjugate state f is formed. Obviously, that it is pointless to solve the conjugate problem and calculate the gradient in such a domain Ω.
on the conjugate state f is formed. Obviously, that it is pointless to solve the conjugate problem and calculate the gradient in such a domain Ω.
It is reasonable to limit ourselves to considering (Fig. 2) the conjugate state of f on the part of Ω, enclosed in the rectangle:
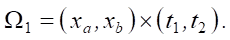
In this case, rectangle Ω1 should be considered too large if the piston is relatively close to the beginning of the nozzle, affecting the conjugate state.
In this rectangle Ω1, the set Ω (shaded with different density in Figure 2 from t1 to t2) will correspond to the redundant set ω. That is, in the objective functional J, the interval (t1, t2) will be redundant. At the same time, in the considered domain Ω, there may be unacceptable interference on the left (low density of shading in Ω1) for calculating gradient ∇J.
Redundancy ω is eliminated by further reducing Ω1 to t3 = t1, i.e., when t3 corresponds to the start of the outflow (Fig. 3 a).
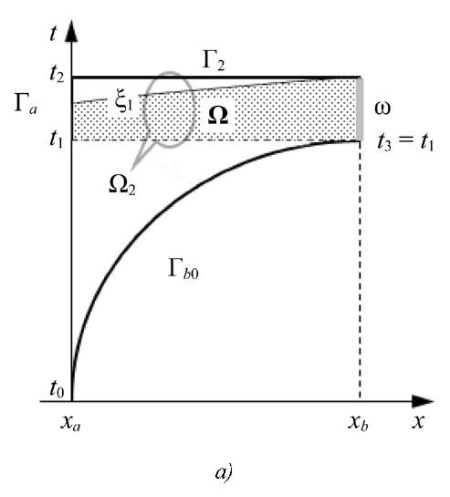
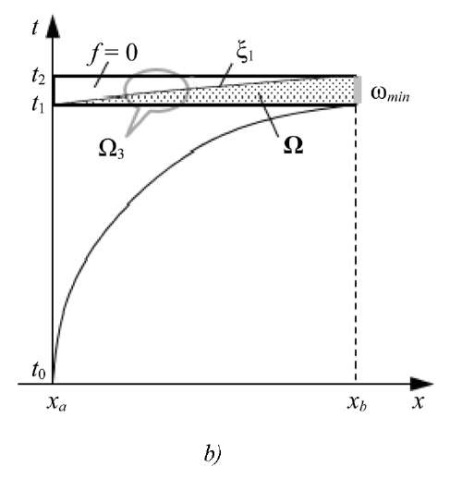
Fig. 3. Space-time diagrams of correct domains Ω for determining the gradient:
a — Ω in domain Ω2; b — Ω in domain Ω3
In this case, the entire domain of a sufficient solution to the conjugate problem is narrowed to an even smaller rectangle:
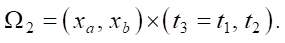
Here, the piston will not “interfere” with the display  .
.
If the technical conditions for designing a hydrocannon allow for an even greater reduction in the flow time t2 – t1, then the solution rectangle of the conjugate problem can be reduced even further, to rectangle Ω3 with a corresponding triangular domain Ω (Fig. 3 b):
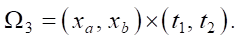
Here there is a minimally sufficient set ωmin to form the domain of definition V*(Ω) of operator 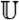 *.
*.
It is in the obtained domains Ω, located inside Ω2 and Ω3 (Fig. 3), that there is a domain of definition V*(Ω) of operator 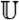 * with a unique mapping of the derivatives
* with a unique mapping of the derivatives 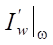 by means of f into the domain of values of gradient U*(S).
by means of f into the domain of values of gradient U*(S).
Conjugate problem (7) and its solution in the rectangles Ω2,3 become significantly simpler:
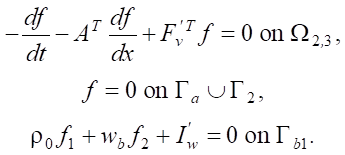 (10)
(10)
Here, Гa = xa × (t1, t2). Now there is no impact of the piston from line Гp, and there is no flow into the nozzle at the boundary Гb0.
Formula (8) for calculating the gradient of the objective functional also takes a simplified form (there is no nonlinear integration boundary Гb0):
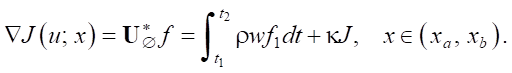 (11)
(11)
The resulting set Ω ⊂ Ω2,3 will correctly define domain V*(Ω) of the definition of operator 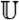 *(Ω) with the range of values in U*(S). The corresponding expression for the time required to form such Ω depends on the characteristics of the first family ξ1 and has the form:
*(Ω) with the range of values in U*(S). The corresponding expression for the time required to form such Ω depends on the characteristics of the first family ξ1 and has the form:
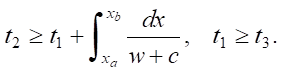 (12)
(12)
That is, firstly, the upper characteristic ξ1 must pass through the entire nozzle from xb to xa. Secondly, the start of the outflow t1 should not be less than the moment t3 of the start of the entry of waves reflected from the piston into the nozzle.
This expression is the controllability condition in the problem under consideration. In this case, the remaining branches of the mappings are fulfilled (9):
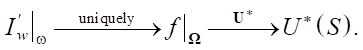
Now we discuss requirement 2) in the theorem on the nondegeneracy of operator 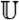 *. Let us start with operator
*. Let us start with operator 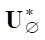 , which defines gradient (8). If the objective function I did not depend explicitly on the control u, then
, which defines gradient (8). If the objective function I did not depend explicitly on the control u, then 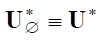 and the set of conjugate states in the kernel fker = {f :
and the set of conjugate states in the kernel fker = {f : 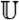 *f = 0 on S} would be zero for an unbounded optimal control u*. In our case, for
*f = 0 on S} would be zero for an unbounded optimal control u*. In our case, for 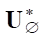 , the values of the elements of the kernel fker will not be zero, i.e., the optimal control will correspond to non-zero conjugate states. The subscript
, the values of the elements of the kernel fker will not be zero, i.e., the optimal control will correspond to non-zero conjugate states. The subscript 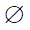 means the absence of a zero kernel. Obviously, if
means the absence of a zero kernel. Obviously, if 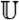 * was nondegenerate, then operator
* was nondegenerate, then operator 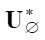 will also be nondegenerate. The nonhomogeneity of operator
will also be nondegenerate. The nonhomogeneity of operator 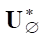 in our problem leads only to a shift in the zero kernel of the homogeneous operator
in our problem leads only to a shift in the zero kernel of the homogeneous operator 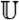 *.
*.
We estimate the possible degeneracy of the homogeneous operator 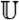 *. It is obvious that for any values of ρ and w, the result of integration in
*. It is obvious that for any values of ρ and w, the result of integration in 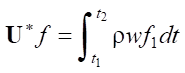 can become zero on S only when f1 = 0 on Ω. This means that operator
can become zero on S only when f1 = 0 on Ω. This means that operator 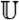 * is nondegenerate, and therefore,
* is nondegenerate, and therefore, 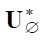 is also nondegenerate.
is also nondegenerate.
The last requirement of the theorem remains. Regularization in the direct extreme approach is provided by:
- selection of the initial approximation u0∈
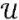 ;
; - subsequent steps of algorithms of type (6) with a satisfactory regularization parameter, i.e., with parameter bk, that does not take the control uk+1 beyond the compact set
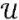 .
.
Paper [8] describes the required regularizing gradient methods for algorithm (6) in the problem under consideration.
Thus, all the requirements of the theorem for providing controllability are met. The distributed system (3) is controllable by u(x) on S according to functional J (5) under condition (12).
Results of Using Controllability Conditions for a Hydrocannon. The parameters of the experimental setup were borrowed from the research of A.N. Semko [15]:
- origin xa=0;
- nozzle length xb=0.253 m;
- initial position of the piston with the left boundary of water xp0= –0.28 m;
- piston mass mp=2.25 kg;
- initial velocity of the piston and water ω0= 76.2 m/s;
- water density at atmospheric pressure ρ0= 103 kg/m3;
- hydrocannon barrel radius Ra= 33 ∙ 10–3m;
- start of water flow into the nozzle t0= 0.
The original problem was solved in a complex closed domain 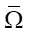 , and conjugate problem — on a small rectangle
, and conjugate problem — on a small rectangle 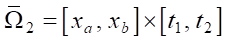 . Two spatial grids were constructed, each containing 50 steps. The first grid was movable and was used to calculate the water flow from the piston to the nozzle exit section, while the second grid was stationary and was designed to describe the nozzle shape. The number of layers over time was variable and reached 103. The exact value depended on the nozzle shape and was determined by the final time t2. The original and conjugate problems were solved by the method of characteristics on identical movable grids in
. Two spatial grids were constructed, each containing 50 steps. The first grid was movable and was used to calculate the water flow from the piston to the nozzle exit section, while the second grid was stationary and was designed to describe the nozzle shape. The number of layers over time was variable and reached 103. The exact value depended on the nozzle shape and was determined by the final time t2. The original and conjugate problems were solved by the method of characteristics on identical movable grids in 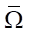 and in
and in 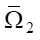 , respectively.
, respectively.
The start of the jet flow from the nozzle was observed at t1 ≈ 2.7 ∙ 10–3 s. The average value of the impulse force of the obtained jet was estimated by objective functional J(u) in the interval t2 – t1 = 3 ∙ 10–4 s. This interval was approximately 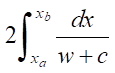 . In this case, the begin time of the flow t1 > t3, i.e., the piston did not affect the flow. Thus, the specified time t2 satisfied the controllability condition (12).
. In this case, the begin time of the flow t1 > t3, i.e., the piston did not affect the flow. Thus, the specified time t2 satisfied the controllability condition (12).
In [8], the required adaptive computational extremal algorithms were implemented taking into account the controllability conditions described here. And the optimal nozzle shapes obtained for the first time were presented.
In Figure 4, nozzle 1 corresponds to the internal local maximum of functional J(u), and nozzle 2 — to the edge maximum under the constraint on nozzle expansion: u(x) ≤ 0, ∀x ∈ S. The first nozzle practically has the shape of a cone, while the second one provides that the objective functional reaches a global maximum, whose value J is approximately three times greater than the value obtained for the first nozzle.
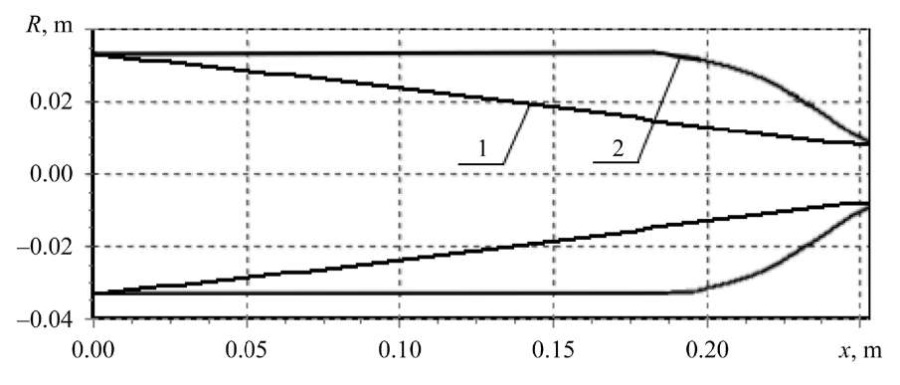
Fig. 4. Optimal shapes of hydrocannon nozzles
The initial approximation u0(x) was set in the form of a pipe — as a continuation of the cannon barrel. At the first iterations of nozzle narrowing, functional J(u) grew with its convexity (growth of the norm ∇J). Then, the convexity changed to concavity (decrease of the norm ∇J), at the end of which there were very small regions of maximum (minimum norm ∇J with concavity of the functional) with a subsequent convex minimum. Nozzle 1 was obtained in the local maximum. The transition through these local extrema was further accompanied by unlimited convex growth of J(u). Only adding a constraint on the control made it possible to stop the uncontrolled expansion of the nozzle on the boundary with reasonable shape 2.
Recall that attempts were previously made to obtain a satisfactory solution using the classical calculus of variations. To do this, the authors [5] and [7] used relaxation methods to find root u* from the required optimality condition 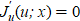 (the Frechet derivative
(the Frechet derivative 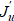 on the incorrect Ω from Figure 2). However, this approach did not give the desired results. Moreover, it requires an additional restriction on the nozzle exit area to prevent its collapse. Such collapse also confirms the incorrectness of using
on the incorrect Ω from Figure 2). However, this approach did not give the desired results. Moreover, it requires an additional restriction on the nozzle exit area to prevent its collapse. Such collapse also confirms the incorrectness of using 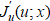 for the directed search for u*(x) without isolating the controllability domain Ω inside Ω2,3. In other words, instead of the Frechet derivative, it is required to obtain a gradient with the justification.
for the directed search for u*(x) without isolating the controllability domain Ω inside Ω2,3. In other words, instead of the Frechet derivative, it is required to obtain a gradient with the justification.
Discussion and Conclusion. The research results show that the application of the controllability analysis proposed in [2] made it possible to identify the key controllability conditions (12) required for the correct formulation and solution of the problem of optimizing the shape of the hydrocannon nozzle.
According to the controllability conditions, the optimization problem must be set and solved in a small rectangular domain Ω2 or even Ω3, and not in a large and complex domain Ω. This is due to the fact that the nozzle shape optimization problem with a statement in Ω does not reduce the Frechet derivative 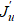 to gradient ∇J, which makes it impossible to search for the optimal solution. It was this circumstance that caused failures of the previous studies, where the optimality of solutions was not proven.
to gradient ∇J, which makes it impossible to search for the optimal solution. It was this circumstance that caused failures of the previous studies, where the optimality of solutions was not proven.
Our recommendations are as follows: first, perform a controllability analysis until the correct controllability domain Ω is identified, and then, for the resulting Ω, identify the solution region of the conjugate problem (in our case, it is Ω2 or Ω3) and find the variation 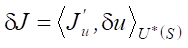 . Next, you can continue the controllability analysis and obtain gradient ∇J from derivative
. Next, you can continue the controllability analysis and obtain gradient ∇J from derivative 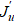 . It is with the help of Ω inside Ω2,3, that you can find the value of gradient ∇J(u; x), which is distributed along the entire nozzle and uniquely corresponds to the objective functional of the problem J(u). And then, you can purposefully search for the optimal nozzle shape.
. It is with the help of Ω inside Ω2,3, that you can find the value of gradient ∇J(u; x), which is distributed along the entire nozzle and uniquely corresponds to the objective functional of the problem J(u). And then, you can purposefully search for the optimal nozzle shape.
The major advantage of the proposed approach is the use of a direct extreme method, which allows for direct maximizing the objective functional using gradient algorithms. This provides not only for the clarity of the controllability analysis, but also the possibility of obtaining numerically confirmed optimal solutions.
The theoretical value of the research is in the development of controllability analysis methods for distributed parameter systems, which opens up new prospects for solving similar problems in other areas. Further research can be aimed at expanding the method for more complex fluid flow models, as well as optimizing other devices operating on the basis of pulsed jets.
References
1. Egorov AI, Znamenskaya LN. Introduction to Distributed Parameter Control Theory. St. Petersburg: Lan; 2022. 292 p. (In Russ.) URL: https://e.lanbook.com/book/167413 (accessed: 10.11.2024).
2. Tolstykh VK. Controllability of Distributed Parameter Systems. Computational Mathematics and Mathematical Physics. 2024;64(6):1211–1223. https://doi.org/10.1134/S0965542524700453
3. Merzlyakov VG, Derevyashkin IV, Boykova IE, Tolmachev AI. Coal and Rock Fracturing by High-Velocity Water Jets. MIAB. Mining Informational and Analytical Bulletin. 2023;(4):140-156. URL: https://giab-online.ru/files/
4. Data/2023/4/04_2023_140-156.pdf (accessed: 10.11.2024).
5. Ocheretyanyi SA, Prokofiev VV. Effect of Cavitator and Nozzle Parameters on the Efficiency Job of the Impulse Jet Generator. Fluid Dynamics. 2023;(5):10–24. https://doi.org/10.31857/S1024708422600981
6. Zuikova ZG. Variational Problem of the Inflow of a Compressible Fluid into a Narrowing Channel. Cand.Sci. (Phys.-Math.), diss. Donetsk: DonSU; 1984. 84 p. (In Russ.)
7. Zubov VI, Zuikova ZG. A Class of Solutions to the Problem of Optimizing the Nozzle of a Water Cannon. Journal of Computational Mathematics and Mathematical Physics. 1994;34(10):1541–1550.
8. Atanov GA. The Optimal Control Problem of Profiling the Hydro-Cannon Nozzle to Obtain the Maximum Outlet Speed. Proceedings of the Institution of Mechanical Engineers, Part C. 1997;211(7):541–547.
9. Tolstykh VK. Algorithms for Optimizing Systems with Multiple Extremum Functionals. Computational Mathematics and Mathematical Physics. 2024;64(3):392–400. https://doi.org/10.1134/S0965542524030163
10. Kabanikhin SI. Inverse Problems of Natural Science. Computational Mathematics and Mathematical Physics. 2020;60:911–914. https://doi.org/10.1134/S0965542520060044
11. Artemyeva LA, Dryazhenkov AA, Potapov MM. Stable Solution of the Quadratic Minimization Problem with a Nonuniformly Perturbed Operator by the Regularized Gradient Method. Computational Mathematics and Mathematical Physics. 2022;62(1):12–22. https://doi.org/10.31857/S0044466922010033
12. Semko AN, Loktyushina JV. About Compressibility of a Liquid at Current Calculation in the Hydrocannon. Bulletin of Donetsk National University. 2011;(2):95–101. URL: https://donnu.ru/public/journals/files/Vestnik_DonNU_2011_
13. N2_compr.pdf#page=96 (accessed: 10.11.2024).
14. Gusev AA. Fundamentals of Hydraulics, 3rd rev. and enl. ed. Moscow: Urait; 2019. 218 p. (In Russ.)
15. Korpusov MO, Panin AA. Lectures on Linear and Nonlinear Functional Analysis. Vol. III. Nonlinear Analysis. Moscow: Lomonosov Moscow State University; 2016. 235 p. (In Russ.)
16. Emelyanov VN. Numerical Methods: Introduction to the Theory of Difference Schemes. Moscow: Urait; 2023. 188 p. (In Russ.)
17. Semko AN. High Velocity Pulsed Liquid Jets and Their Application. Donetsk: DonNU; 2014. 370 p. (In Russ.)
About the Authors
V. K. TolstykhRussian Federation
Victor K. Tolstykh, Dr.Sci. (Phys.-Math.), Professor of the Computer Technology Department
Scopus ID: 6701477776
Researcher ID: JPV-1128-2023
24, Universitetskaya Str., Donetsk, 283001, Donetsk People's Republic
Yu. V. Dmitruk
Russian Federation
Yuliia V. Dmitruk, Senior Lecturer of the Department of General Physics and Didactics of Physics
24, Universitetskaya Str., Donetsk, 283001, Donetsk People's Republic
Review
For citations:
Tolstykh V.K., Dmitruk Yu.V. Controllability Analysis and Optimization of Hydrocannon Nozzle Shape Based on Direct Extreme Approach. Advanced Engineering Research (Rostov-on-Don). 2025;25(1):65-76. https://doi.org/10.23947/2687-1653-2025-25-1-65-76. EDN: RVWIZA
JATS XML














































