Scroll to:
Analytical Modeling of a Heat Source under Welding of a Steel Sleeve by the Centrifugal Method Using an Axisymmetric Electric Arc
https://doi.org/10.23947/2687-1653-2025-25-2-83-90
EDN: PZSKEU
Abstract
Introduction. The technology of centrifugal bimetallization using an independent axisymmetric electric arc is becoming increasingly important due to the high need to improve the quality of bimetallic compositions used in the manufacture of plain bearings, cylinder barrels for hydraulic units, and friction pair elements in internal combustion engines. The existing research in this area emphasizes the need for a more in-depth study of the features of thermal processes associated with this technology. In modern scientific literature, issues related to temperature control at the interface of materials are not fully disclosed, and the existing gap in the concept of the behavior of bimetallic compounds under heating conditions hinders the implementation of this technology in industrial production. The objective of this study is to conduct analytical modeling of a heat source in the form of an axisymmetric electric arc to determine the heat concentration coefficient and reduce the proportion of experimental data in the thermal process model, which will increase its versatility. The tasks arising from the stated goal are comparison of the results of calculating the effective heat flux density from two different expressions (using trigonometric and exponential functions), as well as evaluation of the distribution of the heat flux of an axisymmetric arc along the inner surface of the sleeves (this is required to establish the relationship between the temperature of the outer surface of the welded sleeve and the temperature at the interface between the materials).
Materials and Methods. Direct control of the temperature at the interface between the base material and the deposited layer is difficult, but it is possible to carry out indirect control using the temperature of the outer surface. To determine the relationship between the temperature of the outer surface of the deposited sleeve (billet) and the temperature on its inner surface, i.e., at the interface between the base material and the deposited layer, a heat source was modeled, the heat flux distribution of an axisymmetric electric arc along the inner surface of the sleeve was estimated, and an analytical expression was obtained to determine the heat concentration coefficient.
Results. In the course of the work, an analytical expression was obtained for determining the coefficient of heat concentration, k = 0.945 / R1². It was required for calculating the electric arc parameters considering the distribution of the effective thermal power in the hot spot according to an exponential dependence. To simulate the heat source of the facing process (bimetallization) of the inner surface of steel sleeves with heating by an independent axisymmetric electric arc, the results of calculating the effective heat flux density were compared using two expressions: q = q0 ∙ cos³φ and q = q0 ∙ e–k· r²п. This comparison showed that for calculating temperature fields during facing of the inner surface of steel sleeves (billets) with metal alloys under heating by an independent axisymmetric arc, it was possible to use the analytical exponential form of representation of the heat source.
Discussion and Conclusion. Modeling thermal processes of the centrifugal bimetallization using simplified schemes of uniform distribution of heat flow q = const on the entire free surface of the deposited layer, which simulates the spread of heat of an electric arc, requires the introduction of correction factors and a series of experiments to determine them. In this case, the description of the thermal process in the thermal process model contains a high proportion of experimental data and correction factors. Therefore, in order to exclude most of the experimental components when modeling the heat source and heat flow distribution of the facing process (bimetallization) of the inner surface of steel sleeves under heating by an independent axisymmetric electric arc, the author in this paper proposes an analytical solution for calculating the effective heat flow density in the form of an exponential function. This function allows determining the heat concentration coefficient of an independent axisymmetric electric arc during the facing process, which is required to increase the accuracy of calculating the temperature field of the bimetallized sleeve and improve the temperature control of the thermal parameters of the technological process.
Keywords
For citations:
Glushko S.P. Analytical Modeling of a Heat Source under Welding of a Steel Sleeve by the Centrifugal Method Using an Axisymmetric Electric Arc. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):83-90. https://doi.org/10.23947/2687-1653-2025-25-2-83-90. EDN: PZSKEU
Introduction. In units and mechanisms of various processing equipment, plain bearings are used, for the manufacture of which expensive antifriction and wear-resistant alloys from various metals are used [1]. Mechanical engineering also needs parts for friction pairs of internal combustion engine sleeves, screw-nut sliding gears [2], sleeves for hydraulic machine cylinders operating under high pressure conditions in the range of 50–60 MPa [3]. To improve performance characteristics and reduce the consumption of expensive materials, it is advisable to manufacture these parts from bimetal, in particular, from a steel-bronze composition. For example, laser [4] or thermal spraying [5] can be used to obtain bimetallic compositions. However, with these spraying technologies, it is very difficult to obtain layers 2–4 mm thick with an allowance for roughing and finishing. To deposit layers of sufficient thickness for subsequent processing, it is possible to use powder surfacing according to additive technology with the energy of an electron or laser beam [6], and to obtain coatings from wear-resistant alloys, it is possible to use laser cladding [7]. In the production of metal composites with a metal matrix, laser additive technologies are used [8]. In addition, selective laser melting (SLM) and electron beam melting (EBM) are applied. These are new technologies of rapid additive manufacturing [9], which provide for the production of complex monoliths from metals or alloys by selective melting of powder layers directed according to a CAD model. However, when facing the internal surfaces of sleeves with diameters of 80–250 mm, it is either difficult or impossible to place energy source units inside them.
Due to the complexity of the technical implementation of the listed technologies, the use of centrifugal bimetallization technology with an independent axisymmetric electric arc is becoming increasingly important. In [10], the modeling of the thermal process of centrifugal bimetallization of the inner surface of sleeves is described. There, a simplified scheme of uniform distribution of heat q = const over the entire free surface of the deposited layer was adopted to calculate the temperature field of the bimetallized sleeve, which simulated the spread of heat of an electric arc that moved from end to end of the deposited sleeve at a speed of v = 0.086 m/s (the value of the Peclet number for this case allowed for such imitation). The disadvantage of this scheme is that its use requires the introduction of correction factors and the performance of a series of experiments to determine them. In this case, the model loses its universality, and the proportion of experimental data and correction factors in the description of the thermal process increases.
Analytical modeling of the heat flux density of an electric arc, calculation of the material temperature in the arc hot spot, and description of the temperature field of a bimetallized sleeve (billet) will allow solving the problem that faces the author — to reduce the proportion of experimentally obtained data in the model, increase the accuracy of calculating the temperature field of a bimetallized sleeve, and strengthen control over the temperature of the process.
To evaluate the heat flow distribution of the bimetallization process of sleeves and exclude most of the experimentally obtained data, the following steps must be taken:
- compare the results of calculating the effective heat flux density to a trigonometric function and an exponential function;
- identify the possibility of representing a heat source during facing of the internal surfaces of steel sleeves using the proposed technology with an exponential form to determine the heat concentration coefficient of an independent axisymmetric electric arc during the facing process.
Materials and Methods. This paper studies the technology of centrifugal bimetallization using an independent axisymmetric electric arc, whose diagram is shown in Figure 1.
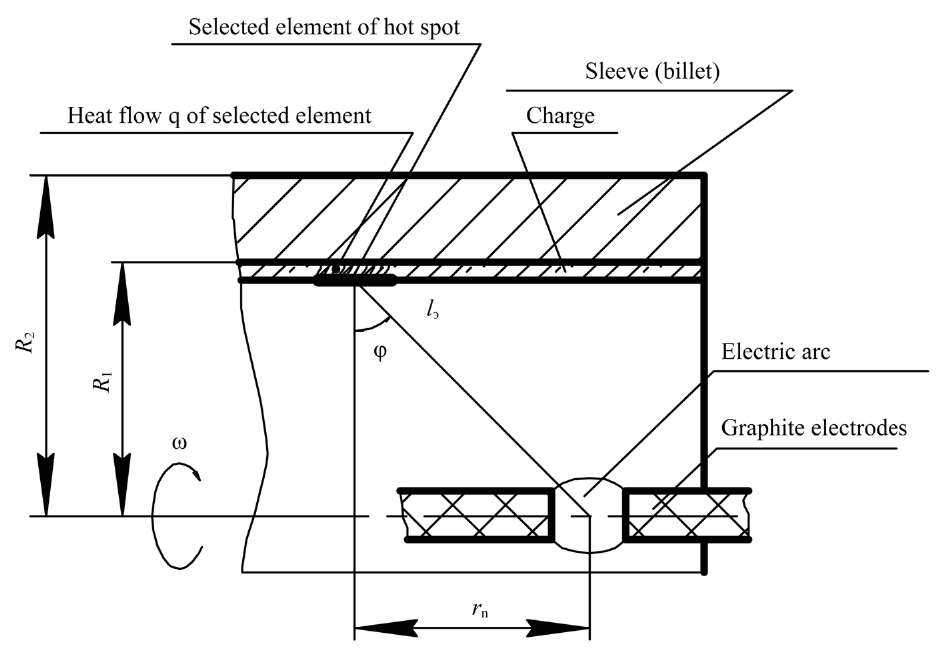
Fig. 1. Scheme of facing the inner surface of a steel sleeve (billet) using centrifugal method through heating by an independent axially symmetrical electric arc
The production of bimetallic sleeves (billets) with heating by an independent electric arc provides high quality of the deposited layer and bimetallic composition if correct temperature control is established at the interface between the deposited layer and the steel base — on the inner diameter of the sleeve R1. In production, direct control of temperature in the diffusion zone is difficult to implement, but indirect control is possible. It is based on the temperature of the outer surface of the steel base at diameter R2 if there is a mathematical model that links the temperature of the outer surface of the welded billet (sleeve) at diameter R2 and the temperature of its inner surface at diameter R1 [10]. To solve this problem, it is necessary to use the heat transport theory [11]. In addition, initial data are needed, including a correct representation of the heat source [12] when calculating the temperature conditions of electric arc processes [10], e.g., bimetallized sleeves with heating by an independent axisymmetric electric arc.
Mathematical models of an electric arc can be divided into two groups according to the method of their construction [13]: theoretical models obtained on the basis of the laws of physics, and experimental models obtained as a result of approximating experimental data using various methods [14].
The use of models in which the heat source is presented as uniformly distributed along the length will not give accurate results for calculating the temperature fields of bimetallized sleeves, since it does not correspond to the real process.
To build a heating model for a bimetallized sleeve, it is proposed to estimate the distribution of the heat flow of an axisymmetric electric arc along the inner surface of the sleeve (billet) [10]. This is easier than modeling thermal processes for nonlinear asymmetric circuits [15].
We represent the problem as a linear one. To simplify the model, let us assume that the length of the billet is large enough to neglect heat losses at the ends. We replace the action of the arc with a point source of constant intensity (Fig. 1). The thermal power of the arc reaches the inner surface of the steel sleeve through the layer of charge practically without losses [1].
For such a scheme, the effective heat flux density on the inner surface of the steel sleeve at diameter R1 is eqAual to:
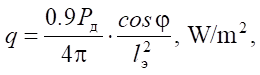 (1)
(1)
where Pд— electric arc power, W; lэ — distance from the center of the arc to the center of the selected element on the inner surface of the steel sleeve, m; φ — angle between the direction of the flow radius vector and the normal to the element of the steel billet irradiated through the charge layer, deg.
At φ = 0, lэ = R1, the heat flux density is maximum:
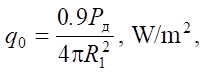
here, R1 — radius of the inner surface of the steel sleeve, m.
Considering that
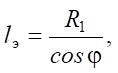
expression (1) can be represented as:
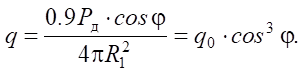 (2)
(2)
We introduce ratio q/q0 = 0.05 into equality (2) and obtain φ = 68°23’, which corresponds to ρ = rn/R = 2.52, where rn — radius of the hot spot, i.e., at a distance close to 2.5–3.0 radii of the billet, the influence of the source is reduced to a minimum.
The distribution of the heat flux density of a point source can be described by the exponential dependence:
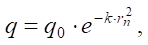 (3)
(3)
where k — heat concentration coefficient, 1/m².
Heat concentration coefficient k is required for calculating the parameters of an electric arc taking into account the distribution of effective thermal power in the hot spot. Determining the value of the heat concentration coefficient is needed for calculating the temperature of the material in the arc hot spot, since the pattern of the heat distribution has a significant effect on the temperature field in the area of the hot spot.
When the arc axis is directed perpendicular to the heating surface, the hot spot is obtained in the form of a circle with a specific flux normally distributed over the area. In this case, the source is called a normally-circular one.
In welding calculation schemes with vertical electrode placement relative to the heating surface, the values of heat concentration coefficients are in the range from 1.5 to 6.0. These schemes, which take into account the distribution of heat sources, are very complex and are rarely used in practice.
For specific cases, the values of parameters q0, q, and k, characterizing the heat flows of an electric arc, are most often determined experimentally.
To determine the preferability of using equalities (2) and (3) to calculate the specific heat flow (using these expressions), it is necessary to obtain an expression by which the heat concentration coefficient k can be calculated. For this purpose, the system of equations (2) and (3) should be solved.
Taking into account that
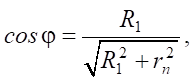
we determine the value of the heat concentration coefficient:
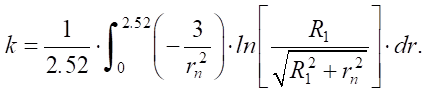
Since cos φ can be represented as
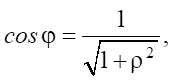
then the heat concentration coefficient will be equal to:
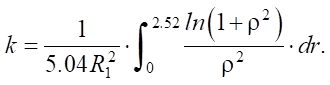 (4)
(4)
We use a variable substitution in the form
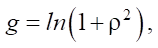
and integrate equation (4) by parts:
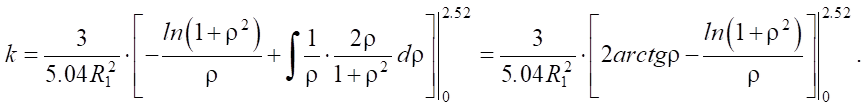
At r = 0, expression ln(1 + ρ²) / ρ is not defined, therefore we use the limit transition:
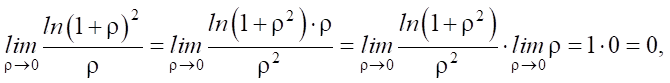
where 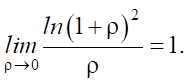
Since 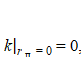 then the heat concentration coefficient will be equal to:
then the heat concentration coefficient will be equal to:
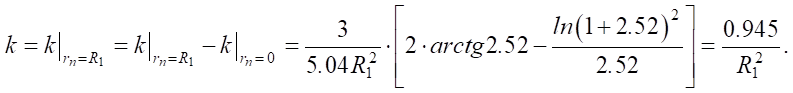 (5)
(5)
Research Results. We use obtained expression (5) to calculate the heat flux density through equation (3), in order to compare the results of calculations using equations (2) and (3) later on.
We compare values 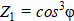 and
and 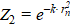 in equalities (2) and (3), setting
in equalities (2) and (3), setting 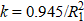 .
.
The calculation results are presented in the form of a nomogram (Fig. 2).
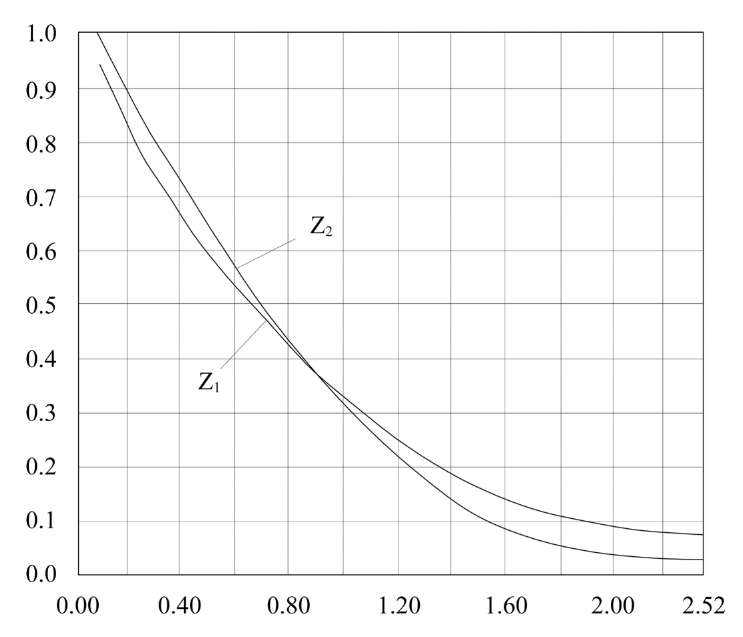
Fig. 2. Nomogram for comparing values 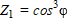 and
and 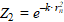 in equalities (2) and (3)
in equalities (2) and (3)
The comparison of the calculated values of 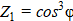 and
and 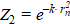 at ρ = 0 ÷ 2.52 have shown that they differ by no more than 10%. This provides using the exponential form of the heat source representation for calculating temperature fields under facing of the inner surface of steel sleeves (billets) with metal alloys heated by an independent axisymmetric arc.
at ρ = 0 ÷ 2.52 have shown that they differ by no more than 10%. This provides using the exponential form of the heat source representation for calculating temperature fields under facing of the inner surface of steel sleeves (billets) with metal alloys heated by an independent axisymmetric arc.
Discussion and Conclusion. To calculate the temperature field of the bimetallized sleeve, a simplified scheme of uniform distribution of the heat flow q = const over the entire free surface of the deposited layer of the electric arc, which reciprocate at a speed of v = 0.086 m/s (the value of the Peclet number for this case allows such imitation), is adopted. The disadvantage of this heat source model is that the heat flux density is determined from the condition of uniform heat distribution, i.e., it is necessary to apply correction factors and conduct a series of experiments to determine them. Thus, the description of the thermal process will contain a high proportion of experimental data and correction factors. Therefore, in order to exclude most of these data when modeling the heat source and heat flow distribution of the facing process (bimetallization) in the method under study, a comparison was made of the results of calculating the effective heat flow density using two expressions: with a trigonometric function and an exponential function. It is found that the exponential form of the heat source representation under facing the inner surfaces of steel sleeves (billets) through the centrifugal method with heating by an independent axisymmetric electric arc can be used to determine the heat concentration coefficient in the facing process. This coefficient is used to determine the density of the heat flow of an electric arc, the temperature at the heating point, and to describe the temperature field of a bimetallized sleeve in analytical form, which increases the accuracy of calculating its temperature field and the ability to control the temperature of a given production process.
References
1. Denisenko SG, Glushko SP. Optimization of Production Technology of Plain Bearings from Steel-Bronze Bimetal. In: Abstracts of the IV Ukrainian Republican Scientific and Technical Conference “Modern Methods of Surfacing, Hardening Coatings and Materials Used”. Kharkov: Kharkov Automobile and Highway Institute; 1990. P. 70–71. (In Russ.)
2. Glushko SP, Denisenko SG. Synthesis of Quality Criterion for Bimetallic Plain Bearings. In: Abstracts of the All-Union Scientific Conference “Structural Strength, Durability, Hardening of Materials and Machine Parts”. Volgograd: Center of Science and Technology; 1990. P. 202–204. (In Russ.)
3. Klevetov DV, Starostin DA. An Approach to Increasing the Durability of Hydraulic Machines by Reducing the Intensity of Wear during Technological Running. In: Proc. All-Russian Sci.-Tech. and Research-Methodological Conference “Modern Problems of Reliability and Technosphere Safety: Education, Science, Practice”, dedicated to the 20th Anniversary of the Department of Life Safety, Ecology and Chemistry, Kovrov State Technological Academy named after V.A. Degtyarev. Kovrov: Degtyarev State Technological Academy; 2019. P. 41–46. (In Russ.)
4. Arias-González F, del Val J, Comesaña R, Penide J, Lusquiños F, Quintero F, et al. Production of Phosphor Bronze Coatings by Laser Cladding. Procedia Manufacturing. 2017;13:177–182. https://doi.10.1016/j.promfg.2017.09.031
5. Kumar RK, Kamaraj M, Seetharamu S, Pramod T, Sampathkumaran P. Effect of Spray Particle Velocity on Cavitation Erosion Resistance Characteristics of HVOF and HVAF Processed 86WC–10Co4Cr Hydro Turbine Coatings. Journal of Thermal Spray Technology. 2016;25(6):1217–1230. https://doi.10.1007/s11666-016-0427-3
6. Frazier WE. Metal Additive Manufacturing: A Review. Journal of Materials Engineering and Performance. 2014;23(6):1917–1928. https://doi.10.1007/s11665-014-0958-z
7. Zhenglei Yu, Lunxiang Li, Deqiang Zhang, Guangfeng Shi, Guang Yang, Zezhou Xu, et al. Study of Cracking Mechanism and Wear Resistance in Laser Cladding Coating of Ni-Based Alloy. Chinese Journal of Mechanical Engineering. 2021;34(92):1–14. https://doi.org/10.1186/s10033-021-00599-8
8. Neng Li, Wei Liu, Yan Wang, Zijun Zhao, Taiqi Yan, Guohui Zhang, et al. Laser Additive Manufacturing on Metal Matrix Composites: A Review. Chinese Journal of Mechanical Engineering. 2021;34(38):1–16. https://doi.org/10.1186/s10033-021-00554-7
9. Murr LE, Gaytan SM, Ramirez DA, Martinez E, Hernandez J, Amato KN, et al. Metal Fabrication by Additive Manufacturing Using Laser and Electron Beam Melting Technologies. Journal of Materials Science & Technology. 2012;28(1):1–14. https://doi.10.1016/S1005-0302(12)60016-4
10. Lawrense AR, Michaleris P. Effects of Thermal Transport in Computation of Welding Residual Stress and Distortion. Science and Technology of Welding and Joining. 2011;16(3):215–220. https://doi.10.1179/1362171810Y.0000000027
11. Glushko SP, Popravka DL, Abramov NS. Modeling the Thermal Process of Centrifugal Bimetallization of the Inner Surface of Bushings. Welding Production. 2009;(6):30–35. (In Russ.)
12. Sudnik VA, Erofeev VA, Maslennikov AV, Tsvelev RV. Methodology of Determining the Equivalent Heat Source Parameters for the Subsequent Calculations of the Structure Distortions. Izvestiya Tula State University. 2015;(6–2):32–43. URL: https://tidings.tsu.tula.ru/tidings/pdf/web/file/tsu_izv_technical_sciences_2015_06_part_2.pdf (accessed: 20.03.2025).
13. Polishchuk V. Mathematical Modeling of Welding Processes. Scientific and Methodological Electronic Journal “Concept”. 2014;20:356–360. URL: http://e-koncept.ru/2014/54332.htm (accessed: 20.03.2025).
14. Vershinin VP, Dmitriev IK. Experimental Research of Temperature Distribution in Tee Joints during Welding. Engineering Journal of Don. 2023;(4):1–9. URL: http://www.ivdon.ru/ru/magazine/archive/n4y2023/8330 (accessed: 20.03.2025).
15. Ivanov SYu, Karhin VA, Michaylov VG. Modelling Welding Processes with Curvilinear Seams. Izvestiya Tula State University. 2015;(6–2):62–66. URL: https://tidings.tsu.tula.ru/tidings/pdf/web/file/tsu_izv_technical_sciences_2015_06_part_2.pdf (accessed: 20.03.2025).
About the Author
S. P. GlushkoRussian Federation
Sergey P. Glushko, Cand.Sci. (Eng.), Associate Professor of the Department of Engineering of Control Systems, Materials and Technologies in Mechanical Engineering
2, Moskovskaya Str., Krasnodar, 350000
An analytical solution for calculating the heat concentration coefficient under bimetallization is presented. Modeling of the heat source shows the advantages of the exponential function for calculating the heat flux density. The study improves temperature control at the interface of materials during the surfacing of sleeves. The results obtained contribute to increasing the accuracy of temperature fields and the quality of bimetallic compositions. New methods provide reducing dependence on experimental data in the bimetallization process.
Review
For citations:
Glushko S.P. Analytical Modeling of a Heat Source under Welding of a Steel Sleeve by the Centrifugal Method Using an Axisymmetric Electric Arc. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):83-90. https://doi.org/10.23947/2687-1653-2025-25-2-83-90. EDN: PZSKEU













































