Перейти к:
Аналитическое моделирование теплового источника при наплавке стальной втулки центробежным методом с использованием осесимметричной электрической дуги
https://doi.org/10.23947/2687-1653-2025-25-2-83-90
EDN: PZSKEU
Аннотация
Введение. Технология центробежной биметаллизации с применением независимой осесимметричной электрической дуги становится всё более значимой ввиду высокой потребности в улучшении качества биметаллических композиций, используемых в производстве подшипников скольжения, гильз для цилиндров гидромашин и элементов пар трения в двигателях внутреннего сгорания. Имеющиеся исследования в этой области подчеркивают необходимость более глубокого изучения особенностей тепловых процессов, связанных с этой технологией. В современной научной литературе недостаточно полно раскрыты вопросы, касающиеся контроля температуры на границе раздела материалов, и имеющийся пробел в представлении о поведении биметаллических соединений в условиях нагрева тормозит внедрение этой технологии в промышленное производство. Цель данного исследования — проведение аналитического моделирования теплового источника в виде осесимметричной электрической дуги для определения коэффициента сосредоточенности тепла и снижения доли экспериментальных данных в модели теплового процесса, что позволит повысить ее универсальность. Задачи, вытекающие из поставленной цели, заключаются в сравнении результатов расчета эффективной плотности теплового потока по двум различным выражениям (с использованием тригонометрической и экспоненциальной функций), а также в оценке распределения теплового потока осесимметричной дуги по внутренней поверхности втулок (это необходимо для установления зависимости между температурой наружной поверхности наплавляемой втулки и температурой на границе раздела материалов).
Материалы и методы. Прямой контроль температуры на границе раздела материала основы и наплавляемого слоя является затруднительным, однако возможно осуществить косвенный контроль с помощью температуры наружной поверхности. Для определения зависимости между температурой наружной поверхности наплавляемой втулки (заготовки) и температурой на её внутренней поверхности, то есть на границе раздела материала основы и наплавляемого слоя, были проведены моделирование теплового источника и оценка распределения теплового потока осесимметричной электрической дуги по внутренней поверхности втулки.
Результаты исследования. В ходе работы получено аналитическое выражение для определения коэффициента сосредоточенности тепла, k = 0,945 / R²1, который необходим для расчёта параметров электрической дуги с учётом распределения эффективной тепловой мощности в пятне нагрева по экспоненциальной зависимости. Для моделирования теплового источника процесса наплавки (биметаллизации) внутренней поверхности стальных втулок с нагревом независимой осесимметричной электрической дугой были сравнены результаты расчета эффективной плотности теплового потока по двум выражениям: q = q0 ∙ cos³φ и q = q0 ∙ e–k· r²п. Это сравнение показало, что для расчетов температурных полей при наплавке внутренней поверхности стальных втулок (заготовок) металлическими сплавами с нагревом независимой осесимметричной дугой можно использовать аналитическую экспоненциальную форму представления теплового источника.
Обсуждение и заключение. Моделирование тепловых процессов центробежной биметаллизации с применением упрощенных схем равномерного распределения теплового потока q = const на всей свободной поверхности наплавляемого слоя, что имитирует распространение тепла электрической дуги, требует введения корректирующих коэффициентов и проведения серии экспериментов для их определения. В этом случае в описании теплового процесса в модели тепловых процессов высока доля экспериментальных данных и корректирующих коэффициентов. Поэтому для исключения большей части экспериментальных составляющих при моделировании теплового источника и распределения теплового потока процесса наплавки (биметаллизации) внутренней поверхности стальных втулок с нагревом независимой осесимметричной электрической дугой автором в данной работе предложено аналитическое решение для расчета эффективной плотности теплового потока в виде экспоненциальной функции, которая позволяет определить коэффициент сосредоточенности тепла независимой осесимметричной электрической дуги в процессе наплавки, который необходим для повышения точности расчета температурного поля биметаллизируемой втулки и улучшения контроля температуры тепловых параметров технологического процесса.
Ключевые слова
Для цитирования:
Глушко С.П. Аналитическое моделирование теплового источника при наплавке стальной втулки центробежным методом с использованием осесимметричной электрической дуги. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):83-90. https://doi.org/10.23947/2687-1653-2025-25-2-83-90. EDN: PZSKEU
For citation:
Glushko S.P. Analytical Modeling of a Heat Source under Welding of a Steel Sleeve by the Centrifugal Method Using an Axisymmetric Electric Arc. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):83-90. https://doi.org/10.23947/2687-1653-2025-25-2-83-90. EDN: PZSKEU
Введение. В узлах и механизмах различного технологического оборудования используют подшипники скольжения, для изготовления которых применяют дорогостоящие антифрикционные и износостойкие сплавы из различных металлов [1]. Машиностроение также нуждается в деталях пар трения гильз двигателей внутреннего сгорания, передач винт-гайка скольжения [2], гильз для цилиндров гидромашин, работающих в условиях высокого давления в диапазоне 50–60 МПа [3]. Для улучшения эксплуатационных характеристик и снижения расхода дорогостоящих материалов целесообразно изготавливать эти детали из биметалла, в частности, из композиции сталь–бронза. Для получения биметаллических композиций можно использовать, к примеру, лазерное [4] или термическое напыление [5]. Но при этих технологиях напыления весьма затруднительно получать слои толщиной в 2–4 мм с припуском для черновой и чистовой обработки. Для наплавки слоев с достаточной для последующей обработки толщиной можно использовать порошковую наплавку по аддитивной технологии с применением энергии электронного или лазерного луча [6], для получения покрытий из износостойких сплавов возможно использование лазерной наплавки [7]. При производстве металлических композитов с металлической матрицей применяют лазерные аддитивные технологии [8]. Кроме того, используют селективную лазерную плавку (SLM) и электронно-лучевую плавку (EBM) — это новые технологии быстрого аддитивного производства [9], которые позволяют изготавливать сложные монолиты из металлов или сплавов путём направленной по CAD-модели селективной плавки порошковых слоёв. Но при наплавке внутренних поверхностей втулок с диаметрами 80–250 мм разместить внутри них узлы источников энергии или затруднительно, или невозможно.
Ввиду сложности технической реализации перечисленных технологий становится всё более значимым применение технологии центробежной биметаллизации с использованием независимой осесимметричной электрической дуги. В работе [10] описано моделирование теплового процесса центробежной биметаллизации внутренней поверхности втулок, где для расчета температурного поля биметаллизируемой втулки была принята упрощенная схема равномерного распределения теплового потока q = const на всей свободной поверхности наплавляемого слоя, что имитирует распространение тепла электрической дуги, которая движется от торца к торцу наплавляемой втулки со скоростью v = 0,086 м/с (значение числа Пекле для этого случая допускает такую имитацию). Недостаток этой схемы заключается в том, что при её использовании требуется введение корректирующих коэффициентов и выполнение серии экспериментов для их определения. Модель в этом случае теряет универсальность, и увеличивается доля экспериментальных данных и корректирующих коэффициентов в описании теплового процесса.
Аналитическое моделирование плотности теплового потока электрической дуги, расчёт температуры материала в пятне нагрева дуги и описание температурного поля биметаллизируемой втулки (заготовки) позволят решить стоящую перед автором задачу — уменьшить долю экспериментально полученных данных в модели, повысить точность расчета температурного поля биметаллизируемой втулки и усилить контроль за температурой технологического процесса.
Для оценки распределения теплового потока процесса биметаллизации втулок и исключения большей части экспериментально полученных данных необходимо предпринять следующие действия:
- сравнить результаты расчета эффективной плотности теплового потока с тригонометрической функцией и экспоненциальной функцией;
- выявить возможность представления теплового источника при наплавке внутренних поверхностей стальных втулок по предлагаемой технологии с помощью экспоненциальной формы для определения коэффициента сосредоточенности тепла независимой осесимметричной электрической дуги в процессе наплавки.
Материалы и методы. В данной работе исследована технология центробежной биметаллизации с применением независимой осесимметричной электрической дуги, схема которой представлена на рис. 1.
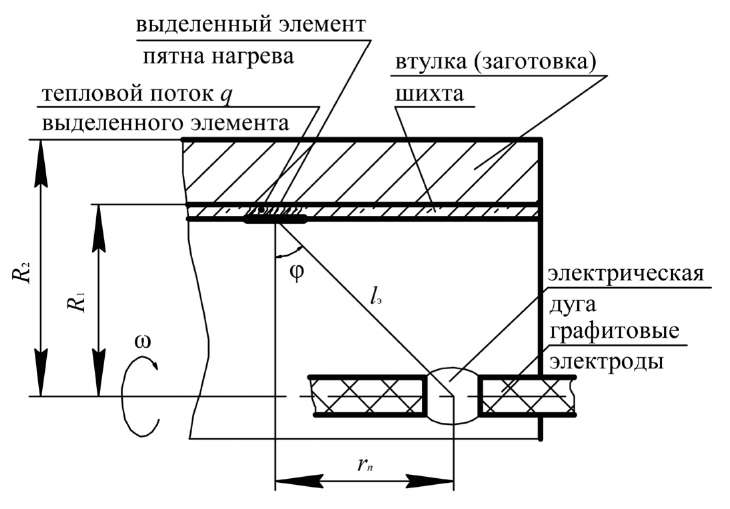
Рис. 1. Схема наплавки внутренней поверхности стальной втулки (заготовки) центробежным способом с нагревом независимой осесимметричной электрической дугой
Производство биметаллических втулок (заготовок) с нагревом независимой электрической дугой обеспечивает высокое качество наплавляемого слоя и биметаллической композиции, если налажен корректный контроль температуры на границе раздела наплавляемого слоя и стальной основы — на внутреннем диаметре втулки R1. В промышленных условиях прямой контроль температуры в зоне диффузии реализовать затруднительно, но возможен её косвенный контроль по температуре наружной поверхности стальной основы на диаметре R2 при наличии математической модели, связывающей температуру наружной поверхности наплавляемой заготовки (втулки) на диаметре R2 и температуру её внутренней поверхности на диаметре R1 [10]. Для решения этой задачи необходимо использовать теорию теплопереноса [11]. Кроме того, нужны исходные данные, в том числе корректное представление теплового источника [12] при расчете температурных режимов электродуговых процессов [10], к примеру, биметаллизируемых втулок с нагревом независимой осесимметричной электрической дугой.
Математические модели электрической дуги можно разделить на две группы по способу их построения [13]: теоретические модели, получаемые на основе законов физики, и экспериментальные, получаемые в результате аппроксимации опытных данных различными методами [14].
Применение моделей, в которых тепловой источник представлен как равномерно распределенный по длине, не даст точных результатов расчета температурных полей биметаллизируемых втулок, так как не соответствует реальному процессу.
Для получения модели нагрева биметаллизируемой втулки предлагается оценить распределение теплового потока осесимметричной электрической дуги по внутренней поверхности втулки (заготовки) [10], это проще, чем моделирование тепловых процессов для нелинейных несимметричных схем [15].
Представим задачу как линейную и для упрощения модели допустим также, что длина заготовки достаточно велика, чтобы пренебречь потерями тепла у торцов. Действие дуги заменим точечным источником постоянной интенсивности (рис. 1). Тепловая мощность дуги доходит до внутренней поверхности стальной втулки сквозь слой шихты практически без потерь [1].
Для такой схемы эффективная плотность теплового потока на внутренней поверхности стальной втулки на диаметре R1 равна:
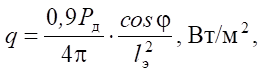 (1)
(1)
где Pд — электрическая мощность дуги, Вт; lэ — расстояние от центра дуги до центра выделенного элемента на внутренней поверхности стальной втулки, м; φ — угол между направлением радиуса-вектора потока и нормалью к облучаемому сквозь слой шихты элементу стальной заготовки, град.
При φ = 0, lэ = R1 плотность теплового потока максимальна:
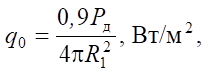
здесь R1 — радиус внутренней поверхности стальной втулки, м.
Поскольку
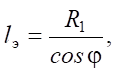
выражение (1) можно представить в виде
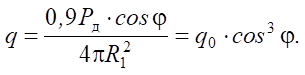 (2)
(2)
Введем в равенство (2) соотношение q/q0 = 0,05 и получим φ = 68°23’, что соответствует ρ = rn/R = 2,52, где rn — радиус пятна нагрева, т. е. на расстоянии, близком к 2,5–3,0 радиусам заготовки, влияние источника сводится к минимуму.
Распределение плотности теплового потока точечного источника может быть описано экспоненциальной зависимостью:
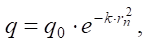 (3)
(3)
где k — коэффициент сосредоточенности тепла, 1/м².
Коэффициент сосредоточенности тепла k необходим для расчёта параметров электрической дуги с учётом распределения эффективной тепловой мощности в пятне нагрева. Определение значения коэффициента сосредоточенности тепла нужно для расчёта температуры материала в пятне нагрева дуги, так как характер распределения теплоты оказывает существенное влияние на температурное поле в области пятна нагрева.
Когда ось дуги направлена перпендикулярно к поверхности нагрева, то пятно нагрева получается в виде окружности с удельным нормально распределенным по площади потоком. В этом случае источник называют нормально-круговым.
В расчетных схемах сварки при вертикальном расположении электродов относительно поверхности нагрева значения коэффициентов сосредоточенности тепла находятся в диапазоне от 1,5 до 6,0. Эти схемы, учитывающие распределение тепла источников, очень сложные и на практике используются редко.
Для конкретных случаев значения параметров q0, q, и k, характеризующие тепловые потоки электрической дуги, чаще всего определяются экспериментально.
Чтобы выяснить предпочтительность применения равенства (2) и (3) для расчета удельного теплового потока (по этим выражениям), нужно получить выражение, по которому можно рассчитывать коэффициент сосредоточенности тепла k. С этой целью следует решить систему уравнений (2) и (3).
С учетом того, что
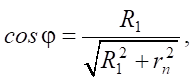
определяем значение коэффициента сосредоточенности тепла:
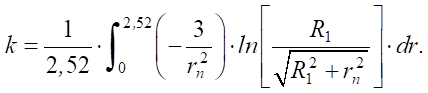
Так как cosφ можно представить в виде:

то коэффициент сосредоточенности тепла будет равен:
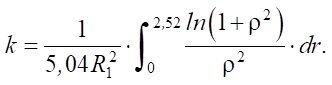 (4)
(4)
Используем замену переменной в виде:
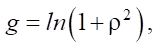
и интегрируем уравнение (4) по частям
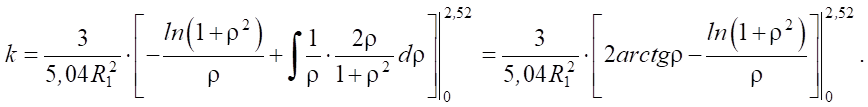
При r = 0 выражение ln(1 + ρ²) / ρ не определено, поэтому используем предельный переход
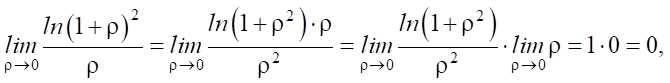
где 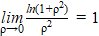 .
.
Так как 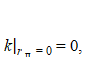 то коэффициент сосредоточенности тепла будет равен:
то коэффициент сосредоточенности тепла будет равен:
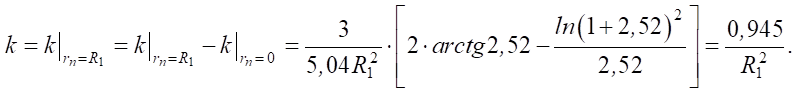 (5)
(5)
Результаты исследования. Используем полученное выражение (5) для расчета плотности теплового потока по уравнению (3), чтобы затем сопоставить результаты вычислений по уравнениям (2) и (3).
Сопоставим значения 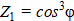 и
и 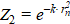 в равенствах (2) и (3), задав
в равенствах (2) и (3), задав 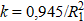 .
.
Результаты расчётов представим в виде номограммы (рис. 2).
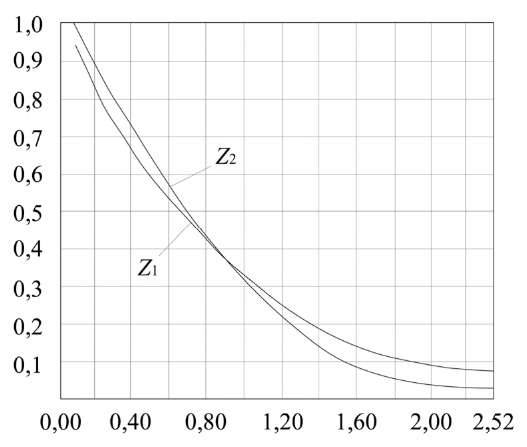
Рис. 2. Номограмма для сопоставления значений  и
и 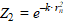 в равенствах (2) и (3)
в равенствах (2) и (3)
Сравнение расчетных значений величин 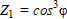 и
и 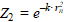 при ρ = 0 ÷ 2,52 показало, что они отличаются не более чем на 10 %. Это позволяет использовать для расчетов температурных полей при наплавке внутренней поверхности стальных втулок (заготовок) металлическими сплавами с нагревом независимой осесимметричной дугой экспоненциальную форму представления теплового источника.
при ρ = 0 ÷ 2,52 показало, что они отличаются не более чем на 10 %. Это позволяет использовать для расчетов температурных полей при наплавке внутренней поверхности стальных втулок (заготовок) металлическими сплавами с нагревом независимой осесимметричной дугой экспоненциальную форму представления теплового источника.
Обсуждение и заключение. Для расчета температурного поля биметаллизируемой втулки принята упрощенная схема равномерного распределения теплового потока q = const на всей свободной поверхности наплавляемого слоя электрической дуги, которая движется возвратно-поступательно со скоростью v = 0,086 м/с (значение числа Пекле для этого случая допускает такую имитацию). Недостаток этой модели теплового источника в том, что плотность теплового потока определена из условия равномерного распределения теплоты, то есть требуется применение корректирующих коэффициентов и проведения серии экспериментов для их определения. Таким образом, в описании теплового процесса будет содержаться высокая доля экспериментальных данных и корректирующих коэффициентов. Поэтому для исключения большей части этих данных при моделировании теплового источника и распределения теплового потока процесса наплавки (биметаллизации) в исследуемом методе проведено сравнение результатов расчета эффективной плотности теплового потока по двум выражениям: с тригонометрической функцией и экспоненциальной функцией. Было установлено, что экспоненциальная форма представления теплового источника при наплавке внутренних поверхностей стальных втулок (заготовок) центробежным способом с нагревом независимой осесимметричной электрической дугой может быть использована для определения коэффициента сосредоточенности тепла в процессе наплавки, этот коэффициент применяется для определения плотности теплового потока электрической дуги, температуры в месте нагрева и описания температурного поля биметаллизируемой втулки в аналитическом виде, что повышает точность расчета ее температурного поля и возможности контроля температуры данного технологического процесса.
Список литературы
1. Денисенко С.Г., Глушко С.П. Оптимизация технологии производства подшипников скольжения из биметалла сталь-бронза. В: Тезисы доклада IV Украинской республиканской научно-технической конференции «Современные методы наплавки, упрочняющие покрытия и используемые материалы». Харьков: Харьковский автомобильно-дорожный институт; 1990. С. 70–71.
2. Глушко С.П., Денисенко С.Г. Синтез критерия качества биметаллических подшипников скольжения. В: Тезисы доклада Всесоюзной научной конференции «Конструкционная прочность, долговечность, упрочнение материалов и деталей машин». Волгоград: Дом науки и техники; 1990. С. 202–204.
3. Клеветов Д.В., Старостин Д.А. Подход к увеличению долговечности гидромашин за счет снижения интенсивности износа при технологической обкатке. В: Труды Всероссийской научно-технической и научно-методической конференции «Современные проблемы надежности и техносферной безопасности: образование, наука, практика», посвященной 20-летию кафедры безопасности жизнедеятельности, экологии и химии Ковровской государственной технологической академии имени В.А. Дегтярева. Ковров: Ковровская государственная технологическая академия имени В.А. Дегтярева; 2019. С. 41–46.
4. Arias-González F, del Val J, Comesaña R, Penide J, Lusquiños F, Quintero F, et al. Production of Phosphor Bronze Coatings by Laser Cladding. Procedia Manufacturing. 2017;13:177–182. https://doi.10.1016/j.promfg.2017.09.031
5. Kumar RK, Kamaraj M, Seetharamu S, Pramod T, Sampathkumaran P. Effect of Spray Particle Velocity on Cavitation Erosion Resistance Characteristics of HVOF and HVAF Processed 86WC–10Co4Cr Hydro Turbine Coatings. Journal of Thermal Spray Technology. 2016;25(6):1217–1230. https://doi.10.1007/s11666-016-0427-3
6. Frazier WE. Metal Additive Manufacturing: A Review. Journal of Materials Engineering and Performance. 2014;23(6):1917–1928. https://doi.10.1007/s11665-014-0958-z
7. Zhenglei Yu, Lunxiang Li, Deqiang Zhang, Guangfeng Shi, Guang Yang, Zezhou Xu, et al. Study of Cracking Mechanism and Wear Resistance in Laser Cladding Coating of Ni-Based Alloy. Chinese Journal of Mechanical Engineering. 2021;34(92):1–14. https://doi.org/10.1186/s10033-021-00599-8
8. Neng Li, Wei Liu, Yan Wang, Zijun Zhao, Taiqi Yan, Guohui Zhang, et al. Laser Additive Manufacturing on Metal Matrix Composites: A Review. Chinese Journal of Mechanical Engineering. 2021;34(38):1–16. https://doi.org/10.1186/s10033-021-00554-7
9. Murr LE, Gaytan SM, Ramirez DA, Martinez E, Hernandez J, Amato KN, et al. Metal Fabrication by Additive Manufacturing Using Laser and Electron Beam Melting Technologies. Journal of Materials Science & Technology. 2012;28(1):1–14. https://doi.10.1016/S1005-0302(12)60016-4
10. Lawrense AR, Michaleris P. Effects of Thermal Transport in Computation of Welding Residual Stress and Distortion. Science and Technology of Welding and Joining. 2011;16(3):215–220. https://doi.10.1179/1362171810Y.0000000027
11. Глушко С.П., Поправка Д.Л., Абрамов Н.С. Моделирование теплового процесса центробежной биметаллизации внутренней поверхности втулок. Сварочное производство. 2009;(6):30–35.
12. Судник В.А., Ерофеев В.А., Масленников А.В., Цвелёв Р.В. Методика определения характеристик эквивалентного источника теплоты для выполнения расчетов деформаций при сварке. Известия Тульского государственного университета. Технические науки. 2015;(6–2):32–43. URL: https://tidings.tsu.tula.ru/tidings/pdf/web/file/tsu_izv_technical_sciences_2015_06_part_2.pdf (дата обращения: 20.03.2025).
13. Полищук В.А. Математическое моделирование процессов сварки. Научно-методический электронный журнал «Концепт». 2014;20:356–360. URL: http://e-koncept.ru/2014/54332.htm (дата обращения: 20.03.2025).
14. Вершинин В.П., Дмитриев И.К. Экспериментальные исследования распределения температуры в тавровых соединениях при сварке. Инженерный вестник Дона. 2023;(4):1–9. URL: http://www.ivdon.ru/ru/magazine/archive/n4y2023/8330 (дата обращения: 20.03.2025).
15. Иванов С.Ю., Кархин В.А., Михайлов В.Г. Моделирование тепловых процессов при сварке соединений с криволинейными швами. Известия Тульского государственного университета. Технические науки. 2015;(6–2):62–66. URL: https://tidings.tsu.tula.ru/tidings/pdf/web/file/tsu_izv_technical_sciences_2015_06_part_2.pdf (дата обращения: 20.03.2025).
Об авторе
С. П. ГлушкоРоссия
Сергей Петрович Глушко, кандидат технических наук, доцент, кафедра «Инженерии систем управления, материалов и технологий в машиностроении»
350072, г. Краснодар, ул. Московская, 2
Представлено аналитическое решение для расчета коэффициента сосредоточенности тепла при биметаллизации. Моделирование теплового источника показывает преимущества экспоненциальной функции для расчета плотности теплового потока. Исследование улучшает контроль температуры на границе раздела материалов в процессе наплавки втулок. Полученные результаты способствуют повышению точности температурных полей и качества биметаллических композиций. Новые методы позволят сократить зависимость от экспериментальных данных в процессе биметаллизации.
Рецензия
Для цитирования:
Глушко С.П. Аналитическое моделирование теплового источника при наплавке стальной втулки центробежным методом с использованием осесимметричной электрической дуги. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):83-90. https://doi.org/10.23947/2687-1653-2025-25-2-83-90. EDN: PZSKEU
For citation:
Glushko S.P. Analytical Modeling of a Heat Source under Welding of a Steel Sleeve by the Centrifugal Method Using an Axisymmetric Electric Arc. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):83-90. https://doi.org/10.23947/2687-1653-2025-25-2-83-90. EDN: PZSKEU












































