Перейти к:
Ab initio расчеты электронно-энергетической структуры и оптических свойств пироцирконатов лантана и неодима
https://doi.org/10.23947/2687-1653-2025-25-2-129-141
EDN: MJOLRM
Аннотация
Введение. Соединения с лантаном и неодимом (La2Zr2O7 и Nd2Zr2O7) обладают низкой теплопроводностью, высокой диэлектрической проницаемостью и температурой плавления, стабильностью и устойчивостью к дефектам. Их можно применять для теплоизоляции металлических компонентов в турбинах и воздушных двигателях. Кроме того, указанные соединения широко исследуются с точки зрения развития материаловедения, особенно при совершенствовании лазерной техники и оптики. Однако физические свойства La2Zr2O7 и Nd2Zr2O7 недостаточно экспериментально изучены. Этот пробел призвано восполнить представленное исследование. Цель работы — модельные расчеты электронной структуры и оптических свойств La2Zr2O7 и Nd2Zr2O7.
Материалы и методы. На основе модельных расчетов в рамках теории функционала плотности исследована электронно-энергетическая структура пироцирконатов La2Zr2O7 и Nd2Zr2O7, содержащих Zr и имеющих кристаллическую структуру пирохлора. В расчетах использовались взятые из литературы параметры кристаллической решетки La2Zr2O7. Из-за отсутствия экспериментальных данных параметры для Nd2Zr2O7 рассчитывались через минимизацию сил, действующих на атомы соединения. Применяется комбинированный обменно-корреляционный потенциал, учитывающий сильные взаимодействия d- и f-электронов атомов La и Nd с поправкой в форме модифицированного метапотенциала Беке-Джонсона. Для расчетов использовался пакет программ Wien2K.
Результаты исследования. Получены плотности электронных состояний всех атомов исследованных соединений. Сравниваются рассчитанные плотности валентных электронных состояний соединений с экспериментальными рентгеновскими фотоэлектронными спектрами. При нулевой энергии рассчитаны значения оптических характеристик La2Zr2O7 и Nd2Zr2O7. Во-первых, это диэлектрическая проницаемость: для La2Zr2O7 — 8,4334, для Nd2Zr2O7 — 8,501. Во-вторых, преломление: для La2Zr2O7 — 2,904, для Nd2Zr2O7 — 2,916. В-третьих, отражение: для La2Zr2O7 — 23,786 %, для Nd2Zr2O7 — 23,935 %. Высокий оптический коэффициент поглощения (˃10⁵ см⁻¹) фиксируется в областях: от 5 до 14 эВ, от 14 до 28 эВ и от 28 до 40 эВ. Пиковые значения экстинкции приходятся на области от 5 до 13 эВ, от 14 до 28 эВ и от 28 до 40 эВ. Кристаллы La2Zr2O7 и Nd2Zr2O7 могут поглощать фотоны в широком диапазоне энергий (4–10 эВ).
Обсуждение и заключение. Исследование дополнило представления о свойствах La2Zr2O7 и Nd2Zr2O7 новыми экспериментальными данными. Рассчитаны плотности электронных состояний и оптические спектры соединений La2Zr2O7 и Nd2Zr2O7. Это позволило объяснить особенности экспериментальных рентгеновских фотоэлектронных спектров соединений. В приближении модифицированного потенциала Беке-Джонсона получены значения ширин запрещенных полос соединений, соответствующие экспериментальным. Исследование относится к фундаментальным и может открыть перспективы создания более эффективных, надежных и функциональных материалов, лазерных и оптических устройств.
Ключевые слова
Для цитирования:
Лаврентьев А.А., Габрельян Б.В., Туан В.В., Калмыкова К.Ф. Ab initio расчеты электронно-энергетической структуры и оптических свойств пироцирконатов лантана и неодима. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):129-141. https://doi.org/10.23947/2687-1653-2025-25-2-129-141. EDN: MJOLRM
For citation:
Lavrentyev A.A., Gabrelian B.V., Tuan V.V., Kalmykova K.F. Ab initio Calculations of the Electronic-Energy Structure and Optical Properties of Lanthanum and Neodymium Pyrozirconates. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):129-141. https://doi.org/10.23947/2687-1653-2025-25-2-129-141. EDN: MJOLRM
Введение. Пироцирконаты лантана и неодима — La2Zr2O7 и Nd2Zr2O7 — относятся к группе пирохлоров. Общая формула этих материалов — A2B2O7. A и B — металлические катионы, которые могут быть трехвалентными (как La и Nd), четырехвалентными (как Zr), двухвалентными и пятивалентными [1]. Пирохлоры обладают высокой диэлектрической проницаемостью, проявляют уникальные магнитные [2], химические, механические и электронные [3] свойства. Благодаря этому их можно использовать как:
- керамические покрытия термобарьеров, газовых сенсоров, металлооксидных транзисторов;
- твердые электролиты в топливных элементах [4];
- иммобилизационные носители актиноидов в ядерных отходах;
- катализаторы окислительных реакций [5];
- элементы магнитных устройств.
Научные изыскания, описанные в данной статье, проводились с учетом развития новых технологий в области лазерной техники, оптики и материаловедения [6]. Результаты работы могут открыть путь к созданию более эффективных, надежных и функциональных устройств [7]. Исследуемые сложные по химическому составу оксиды обладают значительной стабильностью, высокой температурой плавления, большим коэффициентом теплового расширения [8], низкой теплопроводностью, отличной ионной проводимостью и устойчивостью к дефектам [9]. С практической точки зрения важно применение пирохлоров Ln2Zr2O7 в качестве покрытий для обеспечения тепловой изоляции металлических компонентов от горячих газов [10] в турбинах электрогенераторов морских судов и в воздушных двигателях авиалайнеров [11].
Во многих работах (например, в [12]) исследовались физические свойства пирохлоров, включая механические и тепловые. Вместе с тем некоторые их свойства очень трудно оценить и объяснить из-за сильной зависимости от стехиометрии образцов [10]. Расчеты электронно-энергетической структуры различных пирохлоров проводились в рамках теории функционала плотности (например, [13]). В этих расчетах использовались обменно-корреляционные потенциалы, полученные в приближении локальной плотности, обобщенного градиентного приближения, а также псевдопотенциалы.
В [13] отмечена важность коррекции в виде Хаббардовой поправки при расчете незаполненных d- и f-состояний тяжелых атомов [14]. Тем не менее даже с учетом поправки получаемая в расчетах ширина запрещенной зоны часто оказывается меньше, чем экспериментально наблюдаемая [15]. Нужно учесть дополнительные поправки, и именно так поступили авторы представленной работы.
Таким образом, дополнительные экспериментальные и теоретические исследования электронно-энергетической структуры и физических свойств пирохлоров вполне актуальны и имеют практическую значимость.
Рассмотрим кристаллическую структуру пирохлора La2Zr2O7 (пространственная группа Fd-3m, Z = 8) с общей формулой Ln2³⁺Zr2⁴⁺O16O2 (O1 и O2 — атомы кислорода, расположенные в разных кристаллографических позициях). Ее можно описать как структуру дефектного флюорита, в которой катионы образуют гранецентрированную кубическую (fcc) решетку, а 1/8 часть позиций атомов кислорода не занята для обеспечения зарядовой нейтральности (рис. 1).
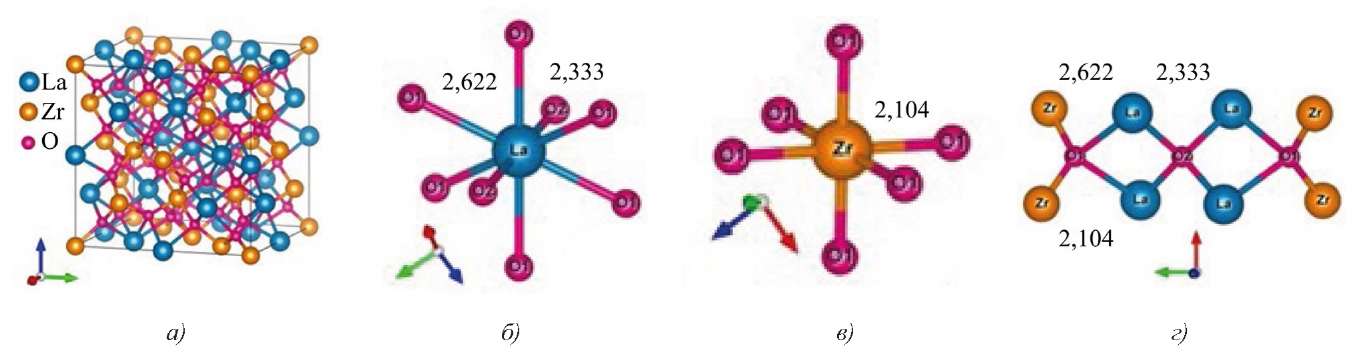
Рис. 1. Кристаллическая структура и ближайшее окружение атомов в пирохлоре La2Zr2O7:
а — элементная ячейка в соединении La2Zr2O7;
б — ближайшее окружение атома La;
в — ближайшее окружение атома Zr;
г — ближайшее окружение атомов кислорода O1 и O2.
Расстояния между атомами даны в Å
Атомы в кристаллической структуре La2Zr2O7 распределены по четырем уникальным кристаллографическим позициям:
- катионы La находятся в Вайкофф-позициях 16d;
- катионы Zr — в позициях 16c;
- кислород O1 — в позиции 48f;
- кислород O2 — в позиции 8b.
Позиции узлов 8а (1/8, 1/8, 1/8) не заняты вообще. Ионы кислорода O2 в узлах 8b (3/8, 3/8, 3/8) стабильны и тетраэдрически координируются катионами редкоземельного элемента La.
Ионы кислорода О1 в позициях 48f (x, 1/8, 1/8) смещены в сторону соседних пустых узлов 8а и окружены двумя катионами La и двумя катионами Zr (рис. 1) [16]. Ближайшее окружение катионов La составляют шесть атомов кислорода O1 (позиции 48f) и два атома кислорода О2 (позиции 8b). Межатомное расстояние La-O2 меньше, чем расстояние La-O1. Катионы Zr (рис. 1) окружены шестью атомами О1 (позиции 48f), находящимися на эквивалентных расстояниях в тригональных антипризмах с точечной симметрией 3m (D3d).
Кристаллические структуры соединений Nd2Zr2O7 и La2Zr2O7 совпадают. В таблице 1 приведены параметры кристаллической решетки исследованных пирохлоров Ln2Zr2O7 (Ln = La, Nd) с пространственной группой Fd-3m, для которой a = b = c, α = β = γ = 90°. Для La2Zr2O7 параметр a и координаты кислорода O1 взяты из работы [15], для Nd2Zr2O7 рассчитаны. Рассчитывалась полная энергия кристалла с разными значениями a и определялось оптимальное значение, соответствующее минимуму полной энергии. Затем атомы кислорода смещались в пределах элементарной ячейки и определялось положение, для которого силы, действующие на атомы, становились минимальными.
Таблица 1
Параметры кристаллической структуры исследованных соединений
|
Соединение, параметр решетки |
Символы Вайкоффа |
x/a |
y/b |
z/c |
|
La2Zr2O7 a = 10,793 Å [15] |
||||
|
La |
16d |
0,50000 |
0,50000 |
0,50000 |
|
Zr |
16c |
0,00000 |
0,00000 |
0,00000 |
|
O1 |
48f |
0,33002 |
0,12500 |
0,12500 |
|
O2 |
8b |
0,37500 |
0,37500 |
0,37500 |
|
Nd2Zr2O7 a = 10,6565 Å |
||||
|
Nd |
16d |
0,50000 |
0,50000 |
0,50000 |
|
Zr |
16c |
0,00000 |
0,00000 |
0,00000 |
|
O1 |
48f |
0,33520 |
0,12500 |
0,12500 |
|
O2 |
8b |
0,37500 |
0,37500 |
0,37500 |
Таким образом, в научной литературе достаточно полно рассмотрены некоторые физические свойства пирохлоров, а также структура соединений Nd2Zr2O7 и La2Zr2O7. Однако физические свойства La2Zr2O7 и Nd2Zr2O7 недостаточно экспериментально изучены. Этот пробел призвано восполнить представленное исследование. Цель работы — модельные расчеты электронной структуры и оптических свойств La2Zr2O7 и Nd2Zr2O7.
Материалы и методы. Выполнены ab initio расчеты электронно-энергетической структуры (ЭЭС) La2Zr2O7 и Nd2Zr2O7 в рамках теории функционала плотности. Применялся метод присоединенных плоских волн с добавлением локальных орбиталей APW+lo. Для реализации задействовали программный пакет WIEN2k [17], в котором используется полный потенциал, не имеющий предопределенной формы, как, например, muffin-tin потенциал.
При построении присоединенной плоской волны применили разложение по l внутри атомной сферы до lmax = 10. В настоящих расчетах использовались следующие радиусы атомных сфер: R(La) = 2,24 a.u., R(Nd) = 2,26 a.u., R(Zr) = 1,96 a.u., R(O) = 1,78 a.u. (1 a.u. = 0,529117 Å). Ряд разложения по плоским волнам обрывался на значениях волнового вектора, определяемых по соотношению = 7, где Rmin — радиус минимальной атомной сферы. Зарядовая плотность разлагалась в ряд Фурье до величины Gmax = 12 (a.u)⁻¹. Плотности электронных состояний получались интегрированием по 1 000 точек в неприводимой зоне Бриллюэна (BZ) методом тетраэдров [18]. Процедура самосогласования проводилась до тех пор, пока не становилось меньше величины q ≤ 0,0001 изменение интегрального заряда q = ∫|ρn – ρn–1|dr. Здесь ρn–1(r) и ρn(r) — электронные плотности, полученные на итерациях n–1 и n соответственно.
Для расчета обменно-корреляционного потенциала использовались:
- приближение обобщенного градиента (англ. generalized gradient approximation, GGA) в параметризации, предложенной авторами [19];
- модифицированный потенциал Беке-Джонсона (англ. modified Becke -Johnson, mBJ [20]).
В дополнение к вышеуказанным обменно-корреляционным потенциалам в расчетах ЭЭС учитывалось сильное кулоновское взаимодействие f-электронов на одном узле Nd [21] в приближении PBE+U [22] с U = 5eV. Таким образом, в окончательном варианте использовались модели обменно-корреляционного потенциала PBE+U и mBJ+U [23].
В Nd2Zr2O7 имеется недостроенная 4f-оболочка с четырьмя f-электронами, поэтому проводили спин-поляризованный расчет ЭЭС. Для атомов La, Nd и Zr учитывалось спин-орбитальное взаимодействие (англ. spin-orbit coupling, SOC). Оно приводит к расщеплению:
- 5p-состояний La и Nd на состояния 5p1/2 и 5p3/2;
- 4p⁶-состояний Zr на состояния 4p1/2 и 4p3/2.
Результаты исследования. В работе рассчитаны полные и парциальные плотности электронных состояний (ППС, англ. density of electron states, DOS). В атоме La нет f-электронов, а в атоме Nd — четыре f-электрона. Несмотря на это различие, в первом приближении рассчитанные полные плотности электронных состояний и экспериментальные рентгеновские фотоэлектронные спектры валентных полос исследованных соединений демонстрируют похожую структуру — четыре области, отражающие вклады s-, p-, d- и f-электронов разных элементов [23].
Данные, приведенные на рис. 2, позволяют сравнить экспериментальный рентгеновский фотоэлектронный спектр (англ. X-ray photoelectron spectrum, XPS) с рассчитанными полными и парциальными плотностями DOS для соединения La2Zr2O7, а рис. 3–5 — для Nd2Zr2O7. Ноль шкалы энергии соответствует вершине валентной полосы EV. Спектры получены в Институте проблем материаловедения имени И.Н. Францевича Национальной академии наук Украины (г. Киев). Особенности эксперимента и оборудование описаны в работе [24].
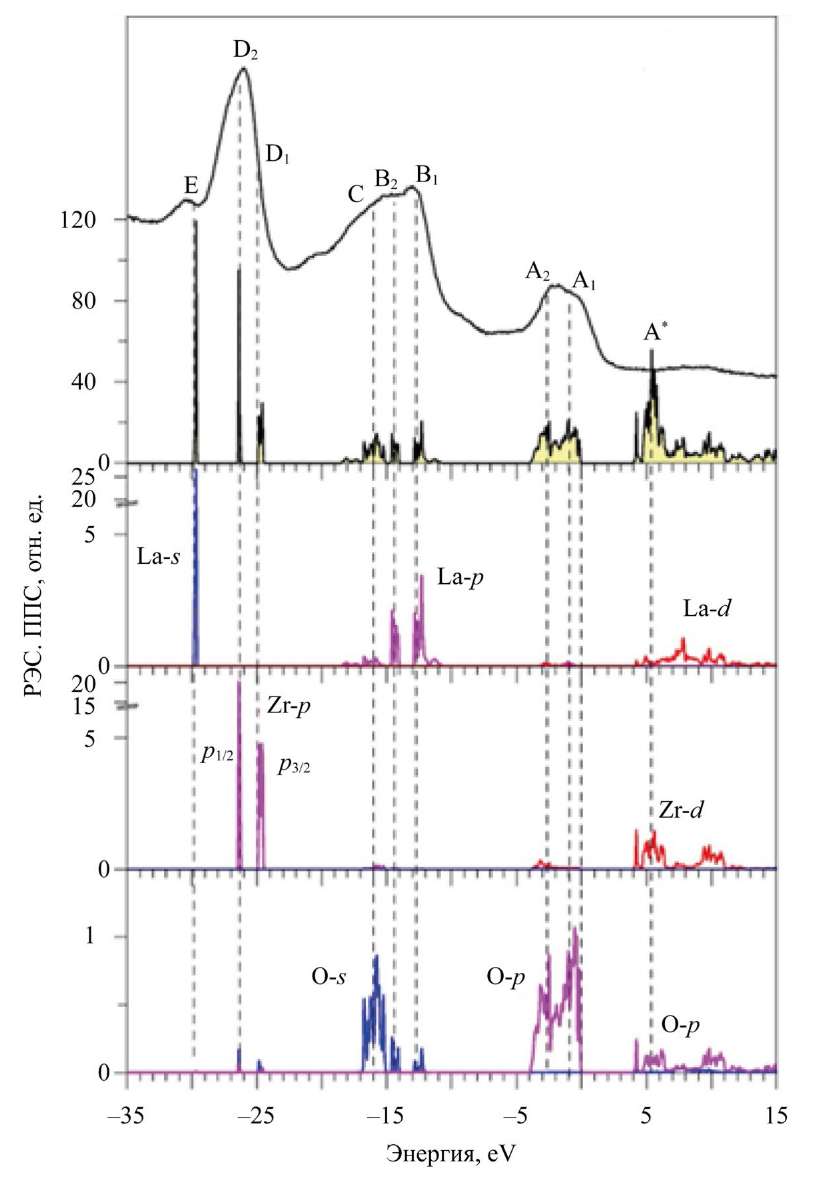
Рис. 2. Рассчитанные в приближении GGA–PBE–SOC полная и парциальные плотности электронных состояний (ППС) в сравнении с экспериментальным рентгеновским фотоэлектронным спектром (РЭС) валентной полосы соединения La2Zr2O7
На рис. 2 в соединении La2Zr2O7 представлена область 1 — верхняя часть валентной полосы от 0 до 4 эВ. Эта область формируется в основном 2p-состояниями кислорода с небольшой примесью 4d-состояний Zr, 5s-состояний Zr, а также 6s- и 5d-состояний La.
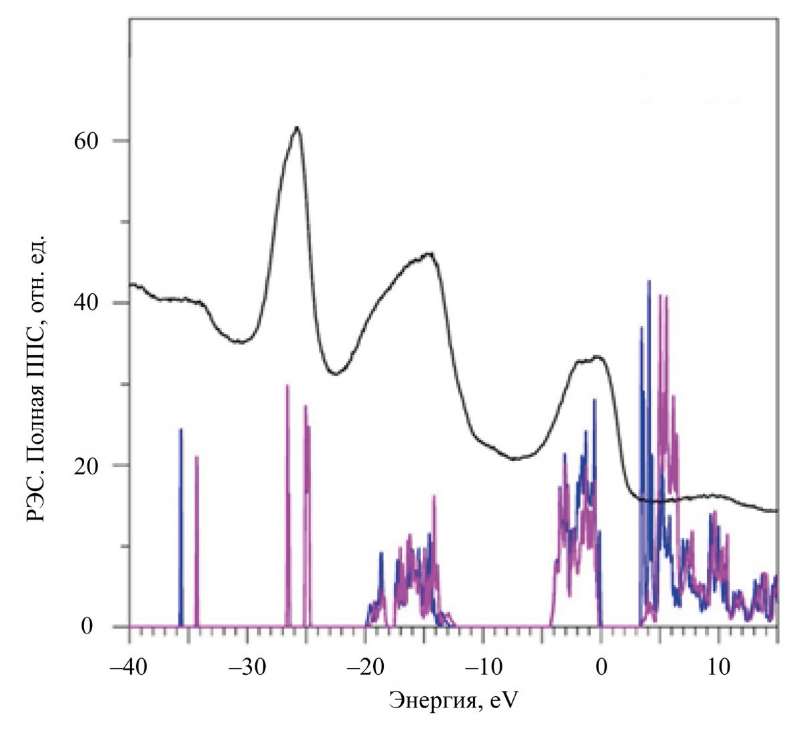
Рис. 3. Рассчитанные в приближении GGA–PBE+U+SOC полные плотности электронных состояний (ППС) со спином вверх и спином вниз в сравнении с экспериментальным рентгеновским фотоэлектронным спектром (РЭС)
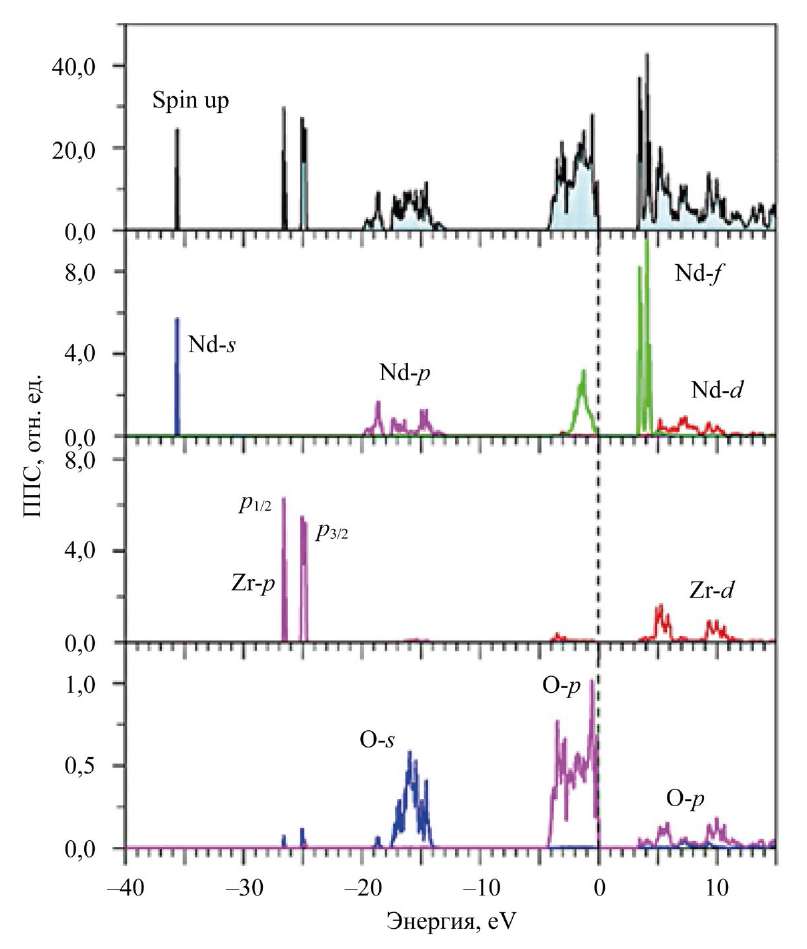
Рис. 4. Рассчитанные в приближении GGA–PBE+U+SOC полная и парциальные плотности (ППС) электронных состояний для спина вверх (spin up) в Nd2Zr2O7
Здесь в Nd2Zr2O7 у вершины валентной полосы располагаются f-состояния Nd со спином вверх. Рентгеновский фотоэлектронный спектр (XPS) подтверждает расчет. Видно, что самый близкий к вершине валентной полосы широкий пик с элементами A1 и А2 в La2Zr2O7 и A в Nd2Zr2O7 соответствует 2p-состояниям атомов кислорода O1 и O2.
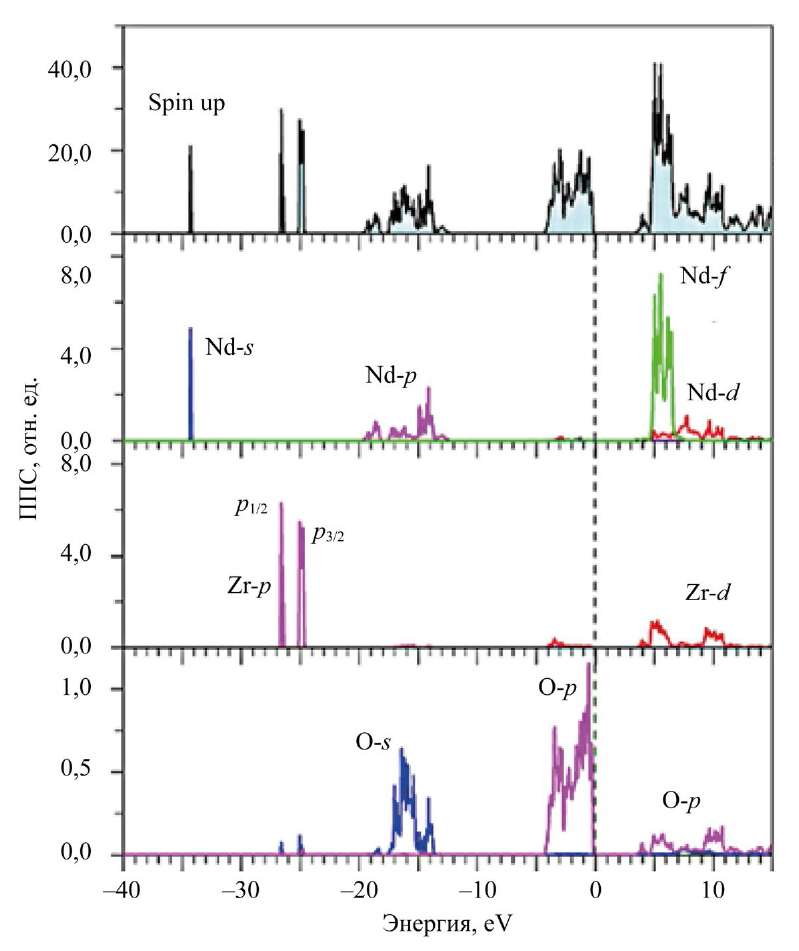
Рис. 5. Рассчитанные в приближении GGA–PBE+U+SOC полная и парциальные плотности электронных состояний (ППС) для спина вниз (spin down) в Nd2Zr2O7
В областях 2, 12–18 эВ от Ev на XPS имеется также широкий пик с особенностями B1, B2 и C для La2Zr2O7 и B для Nd2Zr2O7. Теоретический расчет показывает всю тонкую структуру, которая формирует пик на XPS. 5p⁶-состояния La и Nd расщеплены на состояния 5p1/2- и 5p3/2. Это расщепление проявляется уже в свободных атомах La и Nd [25].
Спин-орбитальное расщепление в свободном атоме присутствует и в твердом теле (рис. 2) на третьей панели снизу для парциальных состояний La. Именно спин-орбитальное расщепление 5p-состояний La приводит к расщеплению 2s-состояний кислорода. Это хорошо видно на самой нижней панели рис. 2, где приведены парциальные состояния кислорода. Как видно из рис. 2, в энергетической области ~12–18 эВ глубоколежащие 5p-состояния La взаимодействуют с 2s-состояниями кислорода. Такое взаимодействие глубоколежащих состояний в твердом теле необычно и связано прежде всего:
- со спин-орбитальным расщеплением 5p-состояний La;
- с тем, что 2s-волновая функция кислорода пространственно и энергетически сильно растянута.
Наличие элементов структуры B1, B2 и С на рентгеновском фотоэлектронном спектре хорошо совпадает с расчетами пика на парциальных плотностях электронных состояний La и O.
Третья область энергий (от 24 до 27 эВ) от Ev — пики D1 и D2 на рентгеновском фотоэлектронном спектре La2Zr2O7, С — на спектре Nd2Zr2O7. Эта область соответствует 4p-состояниям Zr, которые расщепляются в атоме на:
- 4p1/2-состояние с энергией 35 эВ (N2);
- 4p3/2-состояния с энергией 33 эВ (N3).
На кривой XPS La2Zr2O7 расщепление 4p-состояний Zr проявляется в виде асимметрии линий с элементами D1 и D2.
Самые глубоколежащие состояния валентных полос La2Zr2O7 и Nd2Zr2O7 — это уже полуостовные состояния). Четвертая область энергий на XPS-спектре (небольшой пик E на рис. 2, 3) — это 5s-состояния La и Nd. Отметим, что La 5s-состояния в La2Zr2O7 не расщеплены по сравнению с 5s-состояниями Nd с разными направлениями спина (рис. 3). Расщепление 5s-состояний Nd для спина вверх и спина вниз происходит под действием внутреннего магнитного поля. Оно создается четырьмя 4f-электронами, которые выстраиваются одинаково со спином вверх по правилу Хунда [26]. Широкий наплыв D на XPS-спектре (рис. 3) соответствует расщепившимся в теоретическом расчете 5s-состояниям Nd.
Энергетическое распределение электронных состояний в валентной полосе La2Zr2O7 хорошо коррелирует со значениями электроотрицательности (ЭО) элементов [27], входящих в это соединение (таблица 2).
Таблица 2
Электроотрицательность элементов, входящих в исследуемые соединения [27]
|
Элемент |
O |
Zr |
La |
Nd |
Sm |
Eu |
Gd |
|
ЭО |
3,44 |
1,33 |
1,10 |
1,14 |
1,17 |
1,20 |
1,20 |
Итак, самая большая ЭО у кислорода (3,44), поэтому вполне закономерно, что верхняя часть валентной полосы формируется 2p-состоянием O. Примешивание к 2p-состояниям кислорода 4d- и 5s- состояний Zr незначительное, поскольку связь Zr-O1 имеет преимущественно ионный характер. Электроотрицательность кислорода (ЭО = 3,44) значительно выше Zr (ЭО = 1,33) За счет этого, по-видимому, происходит оттягивание 4d- и 5s-электронной плотности Zr к атому кислорода (O1), что характерно для октаэдрического окружения атома Zr атомами О1. В окружении атома La также имеется 6 атомов О1. Электроотрицательность La (ЭО = 1,1) значительно меньше ЭОS = 3,44. Примешивание 5d- и 6s-состояний La почти не наблюдается. Связь атомов La и О1 носит преимущественно ионный характер, доля ковалентности в этой связи весьма небольшая.
Дно полосы проводимости в обоих соединениях формируется в основном незанятыми f- и d-состояниями La/Nd, а также d-состояниями Zr (рис. 2, 4, 5).
Известной проблемой расчетов, использующих обменно-корреляционный потенциал в GGA-приближении, является приуменьшение получаемого значения ширины запрещенной полосы. Для некоторых непроводящих соединений расчеты дают даже проводящее состояние или, как в случае Nd2Zr2O7 в данном расчете, нулевое значение ширины запрещенной полосы. Учет сильного взаимодействия f-электронов в атоме Nd, например в рамках приближения LDA+U (или GGA+U) в расчетах ЭЭС Nd2Zr2O7, приводит к появлению небольшой запрещенной полосы, но близкое к экспериментальным значение можно получить либо в схемах расчета, учитывающих многоэлектронные явления, либо при использовании гибридных или метапотенциалов, таких как модифицированный потенциал Беке-Джонсона (mBJ) [28].
В таблице 3 даны значения ширин запрещенных полос Eg. Их рассчитали с учетом спин-орбитального расщепления (SOC) электронных состояний в атомах La и Nd в приближениях GGA–PBE для La2Zr2O7 (GGA–PBE+SOC) и GGA+PBE+U+SOC (с U = 5eV для 4f-состояний Nd) для Nd2Zr2O7.
Таблица 3
Рассчитанные значения ширин запрещенных полос Eg
|
Соединение |
Обменно-корреляционный потенциал |
Eg, eV |
|
La2Zr2O7 |
GGA–PBE+SOC |
3,928 |
|
Nd2Zr2O7 |
GGA–PBE+U+SOC |
3,393 |
Комплексная диэлектрическая функция ε(ω) = ε1(ω) + iε2(ω) — наиболее важная характеристика для расчета оптического отклика материалов на электромагнитное воздействие. Диэлектрическая функция, в принципе, должна включать в себя как переходы между зонами, так и переходы в пределах зоны. Межзонные переходы разделяются на прямые и непрямые. В данных расчетах игнорируются два фактора. Первый — внутризонные переходы, так как они важны для металлов, а исследуемые соединения — полупроводники. Второй — вклады фононов и других квазичастиц, включенных в непрямые межзонные переходы. Рассматриваются только прямые переходы между занятыми и незанятыми состояниями. Кубическая симметрия кристаллической структуры пирохлора определяет только три ненулевых (диагональных) элемента диэлектрического тензора, причем значения всех этих трех элементов одинаковы.
Рассчитанные кривые действительной ɛ1(ω) и мнимой ɛ2(ω) частей диэлектрической проницаемости для La2Zr2O7 и Nd2Zr2O7 приведены на рис. 6.
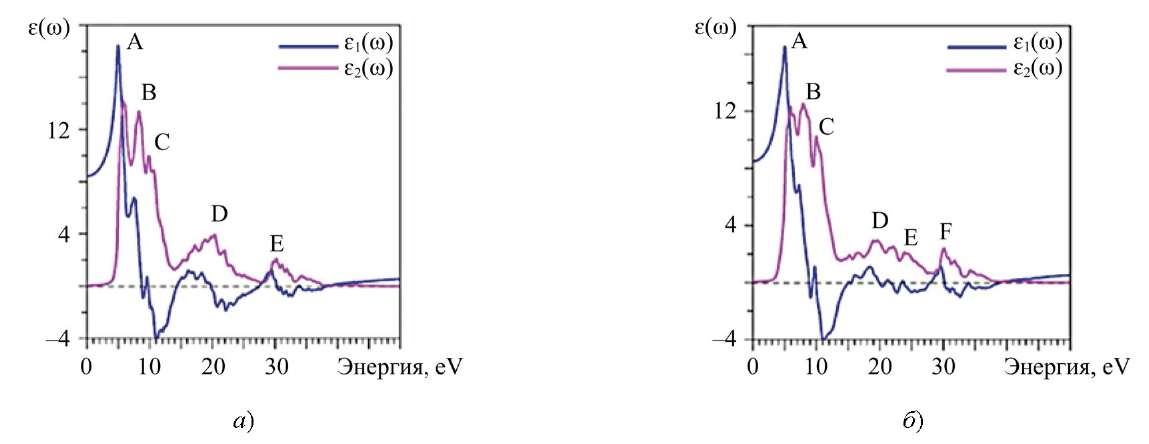
Рис. 6. Рассчитанные действительная (ε1) и мнимая части диэлектрической проницаемости: a — La2Zr2O7; б — Nd2Zr2O7
Спектральные пики поглощающей части диэлектрической функции соответствуют разрешенным дипольным переходам между валентной зоной и зоной проводимости. Для идентификации элементов тонкой структуры необходимо сравнить величины оптических матричных элементов. Наблюдаемые структуры будут соответствовать тем переходам, которые имеют большие значения оптических матричных дипольных элементов перехода. При расчете ɛ2(ω) учитывались только дипольные переходы внутри атома, т.е. без перекрестных переходов. Интерпретация пиков A, B, C, D, E, F на рис. 6 для ɛ2(ω) приведена в таблице 4.
Таблица 4
Интерпретация основных максимумов ɛ2(ω)
|
Соединение |
Пик |
Энергия, eV |
Атом |
Переход |
|
La2Zr2O7 |
A |
≈ 5 |
O |
p → s(d) |
|
B |
≈ 8 |
O |
p → s |
|
|
C |
≈ 10 |
O |
p → s |
|
|
D |
≈ 20 |
O La |
p → s 5p → d |
|
|
E |
≈ 30 |
Zr |
4p → d |
|
|
Nd2Zr2O7 |
A |
5,07 |
O |
p → s |
|
B |
7,8 |
O |
p → s |
|
|
C |
10,2 |
O |
p → s |
|
|
D E |
19,09 24,02 |
O Nd |
p → s 5p → d |
|
|
F |
30,11 |
Zr |
4p → d |
На рис. 6 отражен процесс, когда электроны p-симметрии в верхней части валентной полосы (пик А на XPS) переходят к состояниям s- и d-симметрии в зоне проводимости атома кислорода. Так сформировался самый высокий пик кривой мнимой части диэлектрической функции ɛ2(ω), охватывающей диапазон 5–8 эВ.
Второй и третий по высоте пики кривой ɛ2(ω) — B и C с энергиями 8,28 и 9,86 эВ соответственно. Они обусловлены переходами валентных p-электронов кислорода на свободные состояния s-симметрии кислорода. Рассмотрим широкий максимум D на кривой ɛ2(ω). Частокол из небольших дополнительных пиков появился за счет переходов электронов s-симметрии кислорода на свободные состояния p-симметрии кислорода. Кроме того, в пике D (энергия ̴ 20 эВ), есть вклад переходов валентных 5p-электронов La на свободные в зоне проводимости d-состояния La. Наконец, небольшой пик Е (энергия ̴ 30 эВ) соответствует переходу валентных 4p-электронов Zr на незанятые d состояния Zr. При нулевой энергии рассчитанное значение ɛ2(0) для La2Zr2O7 равно 8,4334, а для Nd2Zr2O7 — 8,501.
Все другие оптические свойства могут быть выведены из ɛ1(ω) и ɛ2(ω). Это, например: коэффициент поглощения α(ω), показатель преломления n(ω), коэффициент экстинкции k(ω), оптический коэффициент отражения R(ω) и спектр энергетических потерь L(ω) [28].
Высокий оптический коэффициент поглощения α(ω) ˃ 10⁵ см⁻¹ [29] фиксируется в трех ярко выраженных областях: от 5 до 14 эВ, от 14 до 28 эВ и от 28 до 40 эВ (рис. 7). По-видимому, такое поглощение может указывать на перспективность использования тонкопленочных элементов из La2Zr2O7 и Nd2Zr2O7.
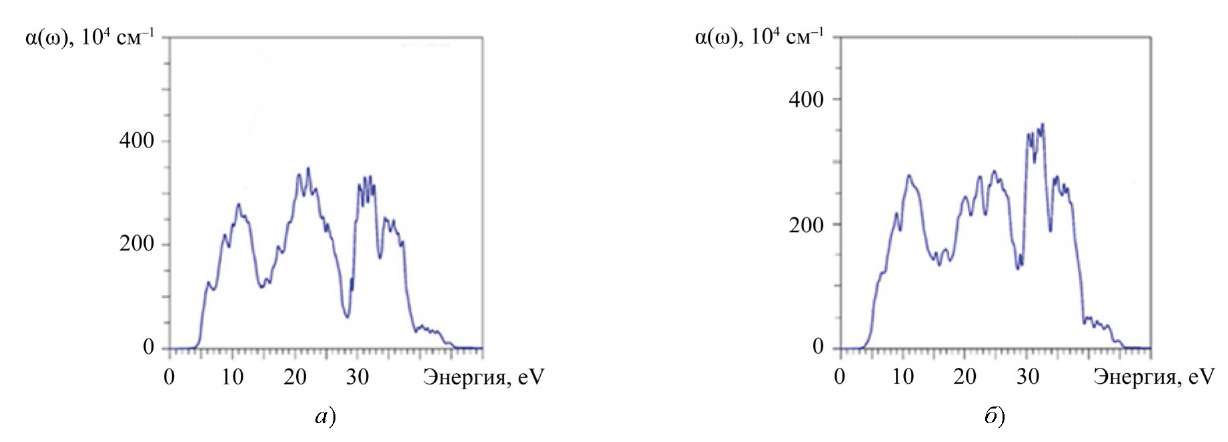
Рис. 7. Рассчитанный коэффициент поглощения α(ω): а — La2Zr2O7; б — Nd2Zr2O7
Кроме того, спектр оптического поглощения характеризуется большим количеством пиков. Они формируются благодаря переходам между занятыми уровнями валентной зоны и свободными уровнями зоны проводимости, разрешенными правилами отбора (Δl ≠ 0) и относящимися к одному атому (перекрестные переходы между соседними атомами маловероятны). Такой частокол небольших пиков на кривой а(ɷ), несомненно, связан с особенностями описанного выше электронно-энергетического строения La2Zr2O7 и Nd2Zr2O7. Вероятно, его нужно учесть при использовании этих соединений в оптоэлектронике.
Комплексный показатель преломления N(ω) = n(ω) + ik(ω) можно получить из комплексной диэлектрической функции ɛ(ω), причем показатель преломления n(ω) зависит в основном от действительной части ɛ1(ω), а коэффициент экстинкции k(ω) — от мнимой части диэлектрической функции ɛ2(ω) [30].
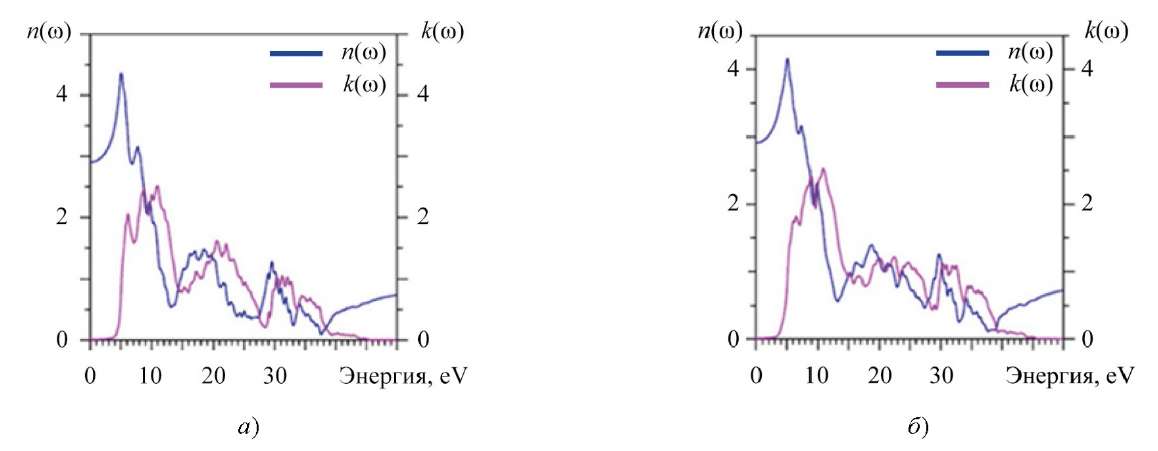
Рис. 8. Рассчитанные показатель преломления n(ω) и коэффициент экстинкции k(ω): а — La2Zr2O7; б — Nd2Zr2O7
При нулевой энергии рассчитанное значение n(0) (статический показатель преломления) для La2Zr2O7 равно 2,904, а для Nd2Zr2O7 — 2,916.
Коэффициент экстинкции k(ω), ответственный за поглощение падающей на кристалл электромагнитной волны, получен из мнимой части диэлектрической функции ɛ2(ω) (рис. 6), поэтому здесь имеются также три области, где величина k(ω) возрастает от 5 до 13 эВ, от 14 до 28 эВ и от 28 до 40 эВ. Затухание интенсивности, представленное коэффициентом экстинкции k(ω), начинается с уменьшением функции n(ω) (рис. 8). Кристаллы La2Zr2O7 и Nd2Zr2O7 могут поглощать фотоны в широком диапазоне энергий (4–10 эВ).
В целом, коэффициент экстинкции La2Zr2O7 и Nd2Zr2O7 не является изотропным и имеет три хорошо выраженные области (энергии указаны выше), где не наблюдается изотропное поведение k(ω). В этих областях различие значений k(ω) составляет 25–50 %.
Коэффициент отражения R(ω) показан на рис. 9. Спектр R(ω) состоит из трех ярко выраженных энергетических областей. Эта же особенность отмечалась для других оптических характеристик. При нулевой энергии рассчитанное значение R(0) для La2Zr2O7 равно 23,786 %, а для Nd2Zr2O7 — 23,935 %.
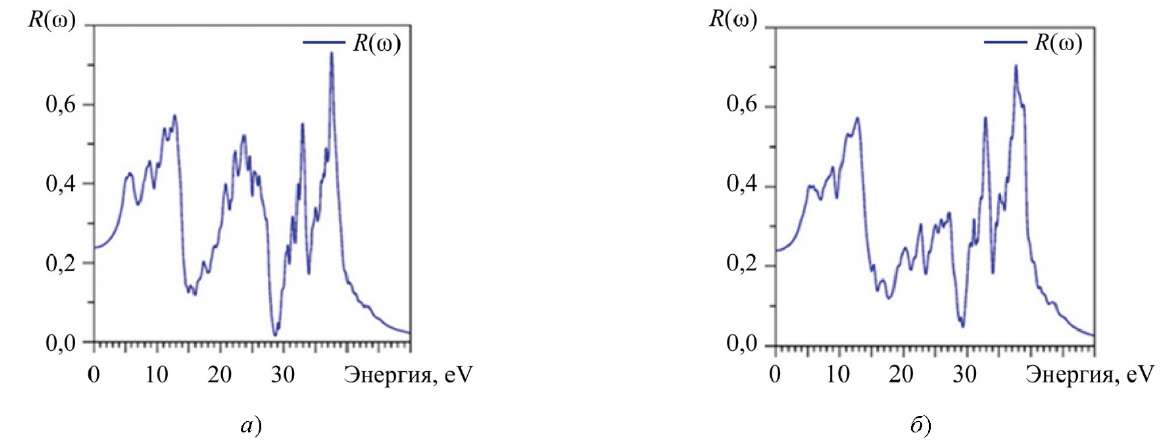
Рис. 9. Рассчитанный коэффициент отражения R(ω): a — La2Zr2O7; б — Nd2Zr2O7
Из рис. 8 видно, что не поглощаются падающие фотоны с энергией, меньшей, чем энергия запрещенной щели ( ̴ 4 эВ). Фотоны с энергией от 4 эВ до ̴ 40 эВ поглощаются кристаллами La2Zr2O7, Nd2Zr2O7 и возбуждают электроны в зоне проводимости, а в валентной зоне образуются положительно заряженные дырки. Однако часть энергии фотона будет потеряна при термализации, и ее отражает спектр энергетических потерь электрона L(ω), приведенный на рис. 10.
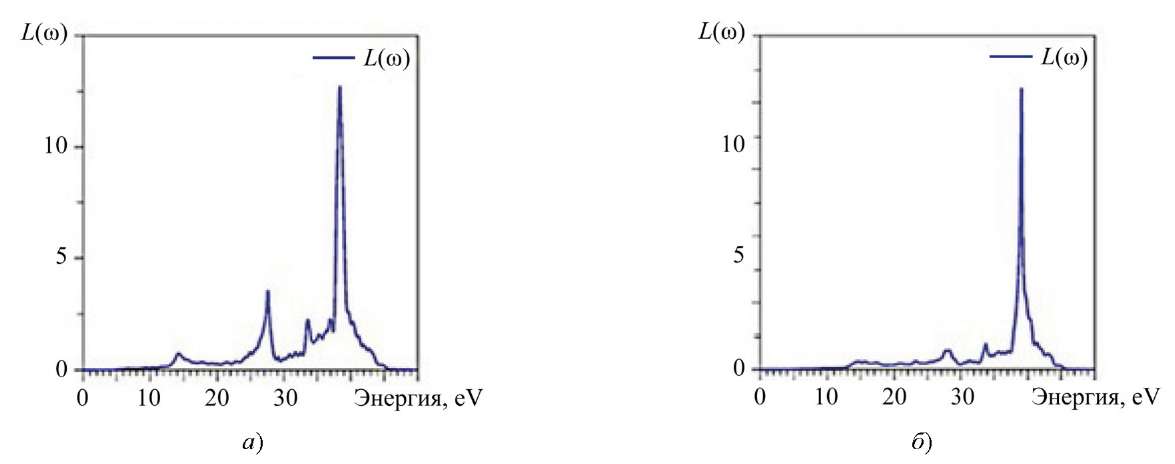
Рис. 10. Рассчитанный спектр энергетических потерь электрона: a — La2Zr2O7; б — Nd2Zr2O7
Потери энергии электроном становятся значительными при 14 эВ (маленький пик), ̴ 27 эВ, ̴ 33,5 эВ. Наибольшая величина R(ω) достигается при 39 эВ, что соответствует резко понижающему краю коэффициента поглощения а(ɷ) (рис. 7).
Обсуждение и заключение. Расчет плотностей электронных состояний валентных полос La2Zr2O7, Nd2Zr2O7 дал два результата:
- позволил объяснить все основные особенности экспериментальных рентгеновских фотоэлектронных спектров этих соединений в области энергий ~35 eV от вершины валентной полосы;
- показал, электроны какой симметрии определили основные особенности экспериментальных спектров.
Вместе с полученными плотностями незанятых состояний рассчитанные плотности занятых состояний позволили вычислить оптические коэффициенты исследованных соединений. Крайне важно учитывать поправки в обменно-корреляционной части потенциала (GGA+U, mBJ). Только с ними удается получить значения ширин запрещенных полос, соответствующие экспериментальным данным. Для Nd2Zr2O7 расчеты без поправок вообще показывают отличную от нуля плотность состояний на уровне Ферми.
Список литературы
1. Chartier A, Meis C, Crocombette J, Corrales LR, Weber WJ. Atomistic Modeling of Displacement Cascades in La2Zr2O7 Pyrochlore. Physical Review B. 2003;67:174102. https://doi.org/10.1103/PhysRevB.67.174102
2. Stanek CR, Minervini L, Grimes RW. Nonstoichiometry in A2B2O7 Pyrochlores. Journal of the American Ceramic Society. 2002;85(11):2792–2798. https://doi.org/10.1111/j.1151-2916.2002.tb00530.x
3. Pirzada M, Grimes RW, Minervini L, Maguire JF, Sickafus KE. Oxygen Migration in A2B2O7 Pyrochlores. Solid State Ionics. 2001;140:201–208. https://doi.org/10.1016/S0167-2738(00)00836-5
4. Tabira Y, Withers RL, Minervini L, Grimes RW. Systematic Structural Change in Selected Rare Earth Oxide Pyrochlores as Determined by Wide-Angle CBED and a Comparison with the Results of Atomistic Computer Simulation. Journal of Solid State Chemistry. 2000;153(1):16–25. https://doi.org/10.1006/jssc.2000.8712
5. Helean KB, Ushakov SV, Brown CE, Navrotsky A, Lian J, Ewing RC, et al. Formation Enthalpies of Rare Earth Titanate Pyrochlores. Journal of Solid State Chemistry. 2004;177(6):1852–1866. https://doi.org/10.1016/j.jssc.2004.01.009
6. Lian J, Zu XT, Kutty KVG, Chen J, Wang LM, Ewing RC. Ion-Irradiation-Induced Amorphization of La2Zr2O7 Pyrochlore. Physical Review B. 2002;66:054108. https://doi.org/10.1103/PhysRevB.66.054108
7. Chen J, Lian J, Wang LM, Ewing RC, Wang RG, Pan W. X-ray Photoelectron Spectroscopy Study of Disordering in Gd2(Ti1-xZrx)2O7 Pyrochlores. Physical Review Letters. 2002;88:105901. https://doi.org/10.1103/PhysRevLett.88.105901
8. Yong Jiang, Smith JR, Odette GR. Prediction of Structural, Electronic and Elastic Properties of Y2Ti2O7 and Y2TiO5. Acta Materialia. 2010;58(5):1536–1543. https://doi.org/10.1016/j.actamat.2009.10.061
9. Winter MR, Clarke DR. Thermal Conductivity of Yttria-Stabilized Zirconia-Hafnia Solid Solutions. Acta Materialia. 2006;54(19):5051–5059. https://doi.org/10.1016/j.actamat.2006.06.038
10. Matteucci F, Cruciani G, Dondi M, Baldi G, Barzanti A. Crystal Structural and Optical Properties of Cr-Doped Y2Ti2O7 and Y2Sn2O7 Pyrochlores. Acta Materialia. 2007;55(7):2229–2238. https://doi.org/10.1016/j.actamat.2006.11.008
11. Uno M, Kosuga A, Okui M, Horisaka K, Muta H, Kurosaki K, et al. Photoelectrochemical Study of Lanthanide Zirconium Oxides, Ln2Zr2O7 (Ln = La, Ce, Nd and Sm). Journal of Alloys and Compounds. 2006;420:291–297. https://doi.org/10.1016/j.jallcom.2005.10.072
12. Ciomaga Hatnean M, Lees MR, Balakrishnan G. Growth of Single-Crystals of Rare-Earth Zirconate Pyrochlores, Ln2Zr2O7 (with Ln = La, Nd, Sm, and Gd) by the Floating Zone Technique. Journal of Crystal Growth. 2015;418:1–6. https://doi.org/10.1016/j.jcrysgro.2015.01.037
13. Feng J, Xiao B, Wan CL, Qu ZX, Huang ZC, Chen JC, et al. Electronic Structure, Mechanical Properties and Thermal Conductivity of Ln2Zr2O7 (Ln = La, Pr, Nd, Sm, Eu and Gd) Pyrochlore. Acta Materialia. 2011;59(4):1742–1760. https://doi.org/10.1016/j.actamat.2010.11.041
14. Zheng Li, Wei Pan. Electronic Structure and Transport Properties of La2Zr2O7 Pyrochlore from First Principles. Solid State Phenomena. 2018;281:767–773. https://doi.org/10.4028/www.scientific.net/SSP.281.767
15. Liu B, Wang JY, Zhou YC, Liao T, Li FZ. Theoretical Elastic Stiffness, Structure Stability and Thermal Conductivity of La2Zr2O7 Pyrochlore. Acta Materialia. 2007;55(9):2949–2957. https://doi.org/10.1016/j.actamat.2006.12.035
16. Subramanian MA, Aravamudan G, Subba Rao GV. Oxide Pyrochlores — A Review. Progress in Solid State Chemistry. 1983;15(2):55–143. https://doi.org/10.1016/0079-6786(83)90001-8
17. Blaha P, Schwarz K, Tran F, Laskowski R, Madsen GKH, Marks LD. WIEN2k: an APW+lo Program for Calculating the Properties of Solids. Journal of Chemical Physics. 2020;152(7):074101. https://doi.org/10.1063/1.5143061
18. Blöchl PE, Jepsen O, Andersen OK. Improved Tetrahedron Method for Brillouin-Zone Integrations. Physical Review B. 1994;49(23):16223–16233. https://doi.org/10.1103/PhysRevB.49.16223
19. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Physical Review Letters. 1996;77(18):3865–3868. https://doi.org/10.1103/PhysRevLett.77.3865
20. Tran F, Blaha P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Physical Review Letters. 2009;102(22):226401. https://doi.org/10.1103/PhysRevLett.102.226401
21. Anisimov VI, Solovyev IV, Korotin MA, Czyżyk MT, Sawatzky GA. Density-Functional Theory and NiO Photoemission Spectra. Physical Review B. 1993;48(23):16929–16934. https://doi.org/10.1103/PhysRevB.48.16929
22. Novák P, Boucher F, Gressier P, Blaha P, Schwarz K. Electronic Structure of the Mixed Valence System (YM)2BaNiO5 (M = Ca, Sr). Physical Review B. 2001;63(23):235114. https://doi.org/10.1103/PhysRevB.63.235114
23. Hong Jiang. Band Gaps from the Tran-Blaha Modified Becke-Johnson Approach: A Systematic Investigation. The Journal of Chemical Physics. 2013;138(13):134115. https://doi.org/10.1063/1.4798706
24. Tuan V Vu, Khyzhun OY, Lavrentyev AA, Gabrelian BV, Kalmykova KF, Isaenko LI, et al. Electronic Band Structure and Optical Properties of Li2In2GeSe6 Crystal. Materials Today Communications. 2023;35:105798. https://doi.org/10.1016/j.mtcomm.2023.105798
25. Lotz W. Electron Binding Energies in Free Atoms. The Journal of the Optical Society of America. 1970:60(2):206–210.
26. Lide DR (ed). CRS Handbook of Chemistry and Physics. 87th ed. Boca Raton; London; New York: CRC Press; Taylor & Francis; 2007. 2608 p.
27. Ambrosch-Draxl C, Sofo JO. Linear Optical Properties of Solids within the Full-Potential Linearized Augmented Planewave Method. Computer Physics Communications. 2006;175(1):1–14. https://doi.org/10.1016/j.cpc.2006.03.005
28. Khan SA, Reshak AH. Optoelectronic and Transport Properties of Zintl Phase KBa2Cd2Sb3 Compound. Computational Materials Science. 2014;95:328–336. https://doi.org/10.1016/j.commatsci.2014.07.031
29. Boujnah M, Dakir O, Zaari H, Benyoussef A, Kenz AE. Optoelectronic Response of Spinels CdX2O4 with X = (Al, Ga, In) through the Modified Becke-Johnson Functional. Journal of Applied Physics. 2014;116(12):123703. https://doi.org/10.1063/1.4896110
30. Tuan V Vu, Lavrentyev AA, Doan V Thuan, Chuong V Nguyen, Khyzhun OY, Gabrelian BV, et al. Electronic Properties and Optical Behaviors of Bulk and Monolayer ZrS2: A Theoretical Investigation. Superlattices and Microstructures. 2019;125:205–213. https://doi.org/10.1016/j.spmi.2018.11.008
Об авторах
А. А. ЛаврентьевРоссия
Анатолий Александрович Лаврентьев, доктор физико-математических наук, профессор, заведующий, кафедра «Электротехника и электроника»
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Б. В. Габрельян
Россия
Борис Витальевич Габрельян, кандидат физико-математических наук, доцент, кафедра «Программное обеспечение вычислительной техники и автоматизированных систем»
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Ву Ван Туан
Вьетнам
Ву Ван Туан, кандидат физико-математических наук, ведущий научный сотрудник, «Лаборатория вычислительной физики» института вычислительной науки и искусственного интеллекта, Университет Ван Ланг
Хошимин
К. Ф. Калмыкова
Россия
Ксения Федоровна Калмыкова, ассистент, кафедра «Электротехника и электроника»
344003, г. Ростов-на-Дону, пл. Гагарина, 1
В работе выполнены модельные расчеты электронной структуры соединений La2Zr2O7 и Nd2Zr2O7. Получены плотности электронных состояний и рассчитаны оптические характеристики соединений. Обнаружены высокие коэффициенты поглощения в широком диапазоне энергий. Результаты позволяют объяснить особенности экспериментальных рентгеновских спектров. Исследование открывает новые перспективы в материаловедении и оптике.
Рецензия
Для цитирования:
Лаврентьев А.А., Габрельян Б.В., Туан В.В., Калмыкова К.Ф. Ab initio расчеты электронно-энергетической структуры и оптических свойств пироцирконатов лантана и неодима. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):129-141. https://doi.org/10.23947/2687-1653-2025-25-2-129-141. EDN: MJOLRM
For citation:
Lavrentyev A.A., Gabrelian B.V., Tuan V.V., Kalmykova K.F. Ab initio Calculations of the Electronic-Energy Structure and Optical Properties of Lanthanum and Neodymium Pyrozirconates. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):129-141. https://doi.org/10.23947/2687-1653-2025-25-2-129-141. EDN: MJOLRM
JATS XML














































