Scroll to:
Ab initio Calculations of the Electronic-Energy Structure and Optical Properties of Lanthanum and Neodymium Pyrozirconates
https://doi.org/10.23947/2687-1653-2025-25-2-129-141
EDN: MJOLRM
Abstract
Introduction. Compounds with lanthanum and neodymium (La2Zr2O7 and Nd2Zr2O7) have low thermal conductivity, high permittivity and melting point, stability and resistance to defects. They can be used for thermal insulation of metal components in turbines and air engines. Also, these compounds are widely studied from the point of view of the development of materials science, particularly, for the improvement of laser technology and optics. However, the physical properties of La2Zr2O7 and Nd2Zr2O7 have not been sufficiently studied experimentally. This gap is intended to be filled by the presented study. The research objective includes model calculations of the electronic structure and optical properties of La2Zr2O7 and Nd2Zr2O7.
Materials and Methods. Based on model calculations within the framework of the density functional theory, the electron-energy structure of pyrozirconates La2Zr2O7 and Nd2Zr2O7, containing Zr and having the crystal structure of pyrochlore was investigated. The parameters of the crystal lattice of La2Zr2O7 taken from the literature were used in the calculations. Due to the lack of experimental data, the parameters for Nd2Zr2O7 were calculated by minimizing the forces acting on the atoms of the compound. A combined exchange-correlation potential was used, taking into account the strong interactions of d- and f-electrons of La and Nd atoms with a correction in the form of a modified Becke-Johnson meta-potential. Wien2K software package was used for the calculations.
Results. The densities of electron states of all atoms of the studied compounds were obtained. The calculated densities of valence electron states of the compounds were compared to the experimental X-ray photoelectron spectra. At zero energy, the optical characteristics of La2Zr2O7 and Nd2Zr2O7 were calculated. Firstly, it was the permittivity: for La2Zr2O7 — 8.4334, for Nd2Zr2O7 — 8.501; secondly, refraction: for La2Zr2O7 — 2.904, for Nd2Zr2O7 — 2.916; thirdly, reflection: for La2Zr2O7 — 23.786%, for Nd2Zr2O7 — 23.935%. High optical absorption coefficient (˃10⁵ cm⁻¹) was recorded in the ranges: from 5 to 14 eV, from 14 to 28 eV, and from 28 to 40 eV. Peak extinction values were in the ranges from 5 to 13 eV, from 14 to 28 eV, and from 28 to 40 eV. La2Zr2O7 and Nd2Zr2O7 crystals could absorb photons in a wide energy range (4–10 eV).
Discussion and Conclusion. The study supplemented the concept of the properties of La2Zr2O7 and Nd2Zr2O7 with new experimental data. The densities of electron states and optical spectra of La2Zr2O7 and Nd2Zr2O7 compounds were calculated. This made it possible to explain features of the experimental X-ray photoelectron spectra of the compounds. In the approximation of the modified Becke-Johnson potential, the values of the widths of the forbidden bands of the compounds corresponding to the experimental ones were obtained. The research is fundamental and can open up prospects for creating more efficient, reliable and functional materials, laser and optical devices.
Keywords
For citations:
Lavrentyev A.A., Gabrelian B.V., Tuan V.V., Kalmykova K.F. Ab initio Calculations of the Electronic-Energy Structure and Optical Properties of Lanthanum and Neodymium Pyrozirconates. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):129-141. https://doi.org/10.23947/2687-1653-2025-25-2-129-141. EDN: MJOLRM
Introduction. Lanthanum and neodymium pyrozirconates — La2Zr2O7 and Nd2Zr2O7 — belong to the pyrochlores group. The general formula of these materials is A2B2O7. A and B are metallic cations that can be trivalent (like La and Nd), tetravalent (like Zr), divalent, and pentavalent [1]. Pyrochlores have high dielectric constant. They exhibit unique magnetic [2], chemical, mechanical and electronic [3] properties. Due to this, they can be used as:
- ceramic coatings of thermal barriers, gas sensors, metal oxide transistors;
- solid electrolytes in fuel cells [4];
- immobilization carriers of actinides in nuclear waste;
- catalysts of oxidation reactions [5];
- elements of magnetic devices.
The research described in this paper was conducted taking into account the development of new technologies in the laser technology, optics and materials science [6]. The results of the work may open the way to the creation of more efficient, reliable and functional devices [7]. The studied oxides of complex chemical composition have significant stability, high melting point, high coefficient of thermal expansion [8], low thermal conductivity, excellent ionic conductivity, and resistance to defects [9]. From the practical perspective, it is important to use pyrochlores Ln2Zr2O7 as coatings to provide thermal insulation of metal components from hot gases [10] in turbines of marine electric generators and in aircraft engines [11].
Numerous papers (e.g., [12]) investigated physical properties of pyrochlores, including mechanical and thermal ones. However, some of their properties are very difficult to evaluate and explain due to their strong dependence on the stoichiometry of the samples [10]. Calculations of the electron-energy structure of various pyrochlores were performed within the framework of the density functional theory (e.g., [13]). These calculations used exchange-correlation potentials obtained in the local density approximation, the generalized gradient approximation, and pseudopotentials.
In [13], the importance of the Hubbard correction in calculating the unoccupied d- and f-states of heavy atoms is noted [14]. Nevertheless, even taking into account the correction, the width of the forbidden band obtained in the calculations often turns out to be smaller than the experimentally observed one [15]. Additional corrections must be taken into account, and this is exactly what the authors of the presented work have done.
Thus, additional experimental and theoretical studies on the electron-energy structure and physical properties of pyrochlores are quite relevant and have practical significance.
Let us consider the crystal structure of pyrochlore La2Zr2O7 (space group Fd-3m, Z = 8) with the general formula Ln2³⁺Zr2⁴⁺O16O2 (O1 and O2 are oxygen atoms located in different crystallographic positions). It can be described as a structure of defective fluorite, in which the cations form a face-centered cubic (fcc) lattice, and 1/8 of the oxygen atom positions are unoccupied to provide charge neutrality (Fig. 1).
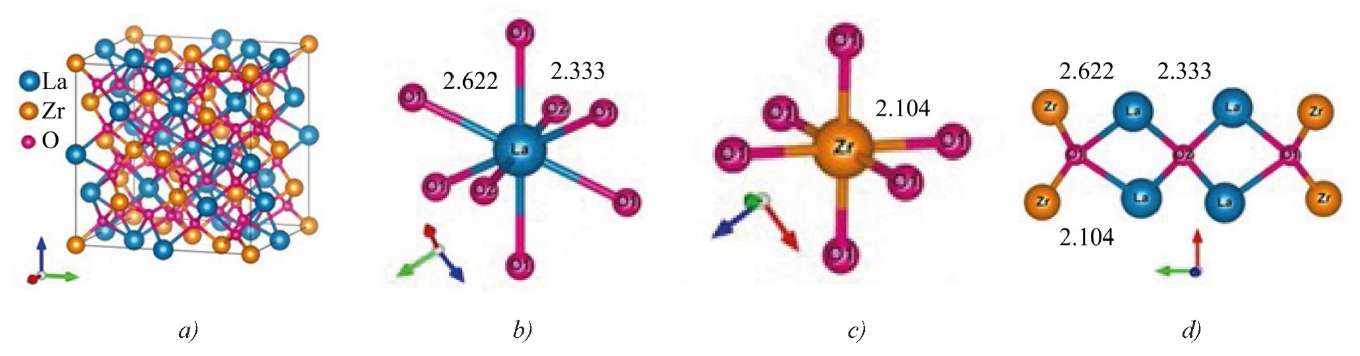
Fig. 1. Crystal structure and immediate environment of atoms in pyrochlore La2Zr2O7:
a — unit cell in compound La2Zr2O7;
b — immediate environment of La atom;
c — immediate environment of Zr atom;
d — immediate environment of oxygen atoms O1 and O2.
Distances between atoms are given in Å
Atoms in the crystal structure of La2Zr2O7 are distributed over four unique crystallographic positions:
- La cations are in Wyckoff positions 16d;
- Zr cations are in positions 16c;
- oxygen O1 is in position 48f;
- oxygen O2 is in position 8b.
The positions of 8а nodes (1/8, 1/8, 1/8) are not occupied at all. Oxygen ions O2 in 8b nodes (3/8, 3/8, 3/8) are stable and tetrahedrally coordinated by the rare earth element cations La.
Oxygen ions О1 in positions 48f (x, 1/8, 1/8) are shifted towards the neighboring empty nodes 8а, and they are surrounded by two La cations and two Zr cations (Fig. 1) [16]. The immediate environment of La cations consists of six oxygen atoms O1 (positions 48f) and two oxygen atoms О2 (positions 8b). La-O2 interatomic distance is shorter than
La-O1 distance. Zr cations (Fig. 1) are surrounded by six О1 atoms (positions 48f), located at equivalent distances in trigonal antiprisms with 3m (D3d) point symmetry.
The crystal structures of Nd2Zr2O7 and La2Zr2O7 compounds coincide. Table 1 shows the crystal lattice parameters of the studied pyrochlores Ln2Zr2O7 (Ln = La, Nd) with the space group Fd-3m, for which a = b = c, α = β = γ = 90°. For La2Zr2O7, parameter a and the coordinates of oxygen O1 are taken from [15], and for Nd2Zr2O7, they are calculated. The total energy of the crystal with different values of a was calculated, and the optimal value corresponding to the minimum of the total energy was determined. Then, the oxygen atoms were displaced within the unit cell and the position, for which the forces acting on the atoms became minimal, was determined.
Table 1
Crystal Structure Parameters of the Studied Compounds
|
Compound, lattice parameter |
Wyckoff symbols |
x/a |
y/b |
z/c |
|
La2Zr2O7 a = 10.793 Å [15] |
||||
|
La |
16d |
0.50000 |
0.50000 |
0.50000 |
|
Zr |
16c |
0.00000 |
0.00000 |
0.00000 |
|
O1 |
48f |
0.33002 |
0.12500 |
0.12500 |
|
O2 |
8b |
0.37500 |
0.37500 |
0.37500 |
|
Nd2Zr2O7 a = 10.6565 Å |
||||
|
Nd |
16d |
0.50000 |
0.50000 |
0.50000 |
|
Zr |
16c |
0.00000 |
0.00000 |
0.00000 |
|
O1 |
48f |
0.33520 |
0.12500 |
0.12500 |
|
O2 |
8b |
0.37500 |
0.37500 |
0.37500 |
Thus, some physical properties of pyrochlores, as well as the structure of compounds Nd2Zr2O7 and La2Zr2O7, have been considered in scientific literature in sufficient detail. However, physical properties of La2Zr2O7 and Nd2Zr2O7 have not been sufficiently studied experimentally. The presented research is intended to fill this gap. The objective of the work is to perform model calculations of the electronic structure and optical properties of La2Zr2O7 and Nd2Zr2O7.
Materials and Methods. Ab initio calculations of the electron-energy structure (EES) of La2Zr2O7 and Nd2Zr2O7 were performed within the framework of the density functional theory. The method of augmented plane waves with the addition of local orbitals APW+lo was used. For the implementation, WIEN2k [17] software package was applied, which used a full potential that did not have a predetermined form, such as muffin-tin potential.
When constructing the attached plane wave, we used the expansion by l inside the atomic sphere up to lmax = 10. The following radii of the atomic spheres were used in the present calculations: R(La) = 2.24 a.u., R(Nd) = 2.26 a.u., R(Zr) = 1.96 a.u., R(O) = 1.78 a.u. (1 a.u. = 0.529117 Å). The series of the expansion in plane waves was interrupted at the values of the wave vector determined by the relation = 7, where Rmin — radius of the minimal atomic sphere. The charge density decomposed into a Fourier series up to value Gmax = 12 (a.u)–1. The densities of electron states were obtained through integrating over 1,000 points in the irreducible Brillouin zone (BZ) using the tetrahedron method [18]. The self-consistency procedure was carried out until the change in the integral charge q = ∫|ρn – ρn–1|dr became less than q ≤ 0.0001. Here, ρn–1(r) and ρn(r) are the electron densities obtained at iterations n–1 and n, respectively.
To calculate the exchange-correlation potential, the following were used:
- generalized gradient approximation (GGA) in the parameterization proposed in [19];
- modified Becke-Johnson potential, mBJ [20].
In addition to the above exchange-correlation potentials, the EES calculations took into account the strong Coulomb interaction of f- electrons at one node Nd [21] in PBE+U approximation [22] with U = 5eV. Thus, in the final version, the exchange-correlation potential models were used PBE+U and mBJ+U [23].
Nd2Zr2O7 has an incomplete 4f-shell with four f-electrons, therefore, a spin-polarized EES calculation was performed. For La, Nd and Zr atoms, spin-orbit coupling (SOC) was taken into account. It resulted in splitting:
- 5p-states of La and Nd into 5p1/2 and 5p3/2 states;
- 4p⁶-states of Zr into 4p1/2 and 4p3/2
Research Results. The paper calculates the total and partial densities of electron states (DOS). Atom La has
no f-electrons, while atom Nd has four f-electrons. Despite this difference, in the first approximation, the calculated total densities of electron states and the experimental X-ray photoelectron spectra of the valence bands of the studied compounds demonstrate a similar structure — four regions reflecting the contributions of s-, p-, d- and f-electrons of different elements [23].
Figure 2 provides comparing the experimental X-ray photoelectron spectrum (XPS) to the calculated total and partial densities DOS for compound La2Zr2O7, and Figures 3–5 — for Nd2Zr2O7. Zero of the energy scale corresponds to the top of the valence band EV. The spectra were obtained at the Frantsevich Institute for Problems of Materials Science, National Academy of Sciences of Ukraine (Kyiv). The experimental features and equipment are described in [24].
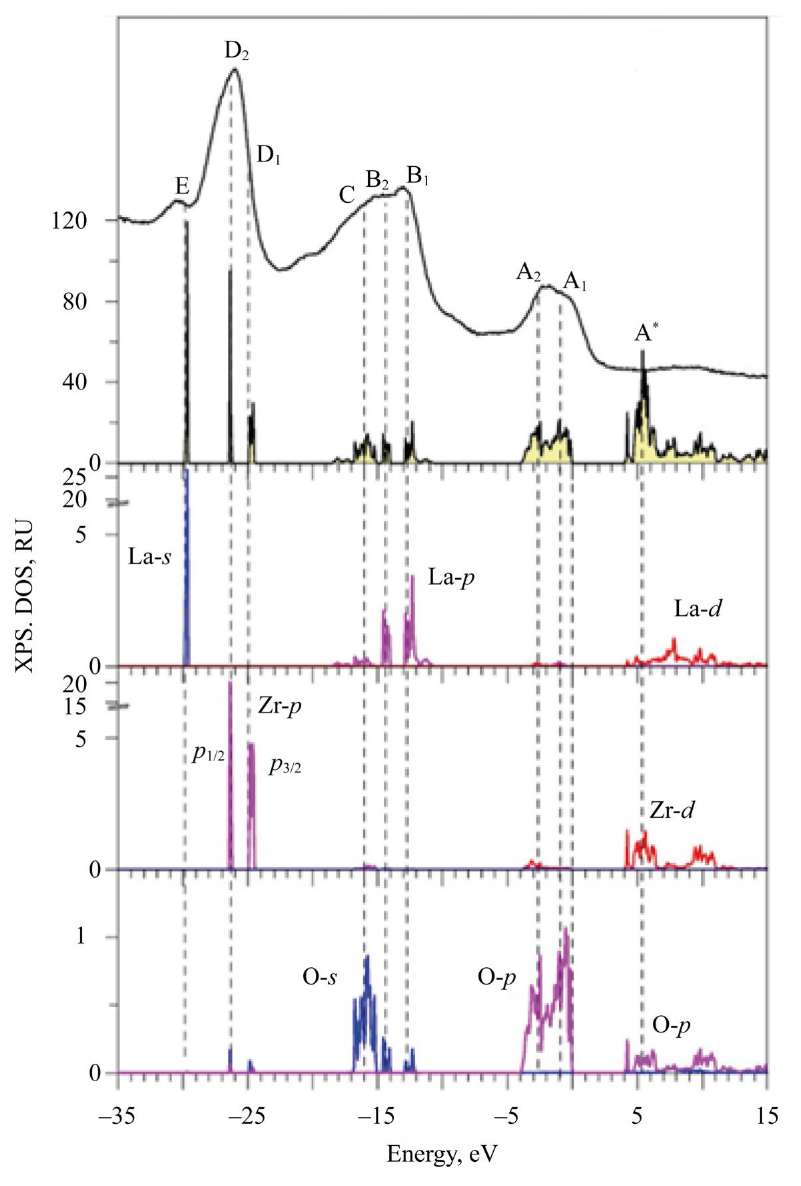
Fig. 2. Total and partial densities of states (DOS) calculated in GGA–PBE–SOC approximation in comparison with experimental X-ray photoelectron spectrum (XPS) of valence band of compound La2Zr2O7
In Figure 2, in compound La2Zr2O7, region 1 is shown— the upper part of the valence band from 0 to 4 eV. This region is formed mainly by 2p-states of oxygen with a small admixture of 4d-states of Zr, 5s-states of Zr, and 6s- and 5d-states of La.
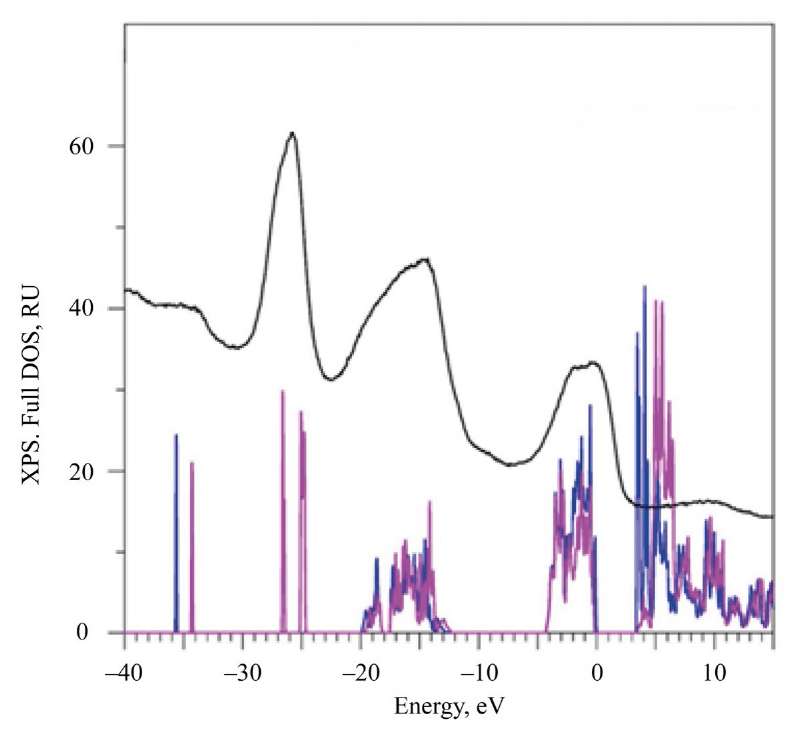
Fig. 3. Total densities of states (DOS) calculated in GGA–PBE+U+SOC approximation with spin up and spin down in comparison with the experimental X-ray photoelectron spectrum (XPS)
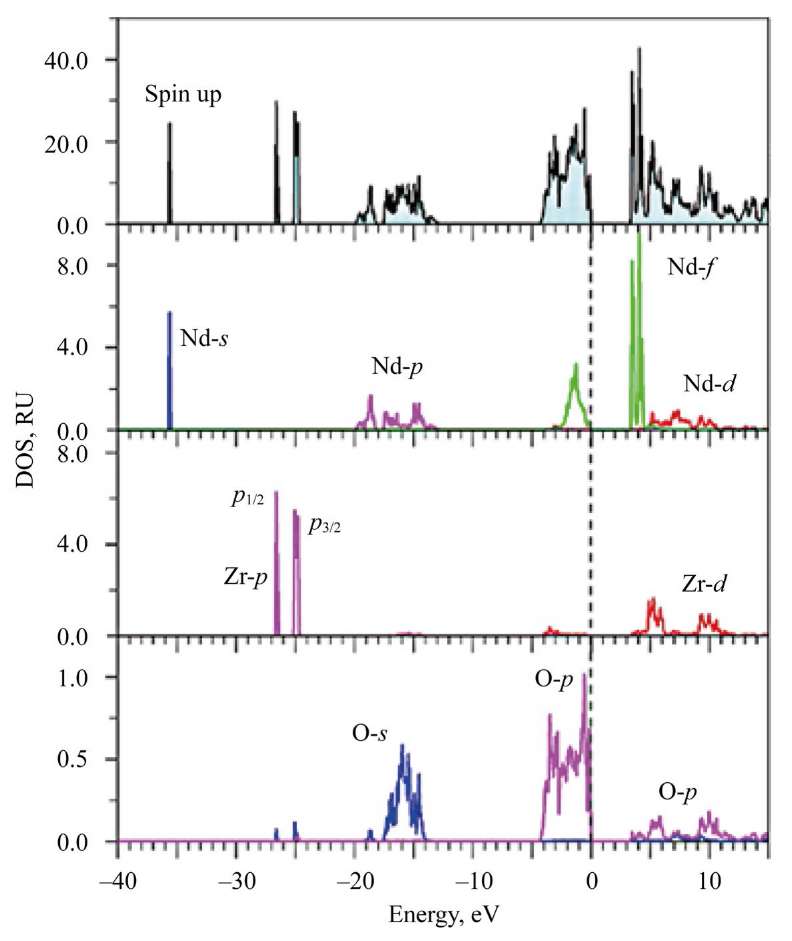
Fig. 4. Total and partial densities of states (DOS) of electrons for spin up in Nd2Zr2O7 calculated in GGA–PBE+U+SOC approximation
Here, in Nd2Zr2O7, at the top of the valence band, f-states of Nd with spin up are located. X-ray photoelectron spectrum (XPS) confirms the calculation. It is seen that the broad peak closest to the top of the valence band with elements A1 and А2 in La2Zr2O7 and A in Nd2Zr2O7 corresponds to 2p-states of oxygen atoms O1 and O2.
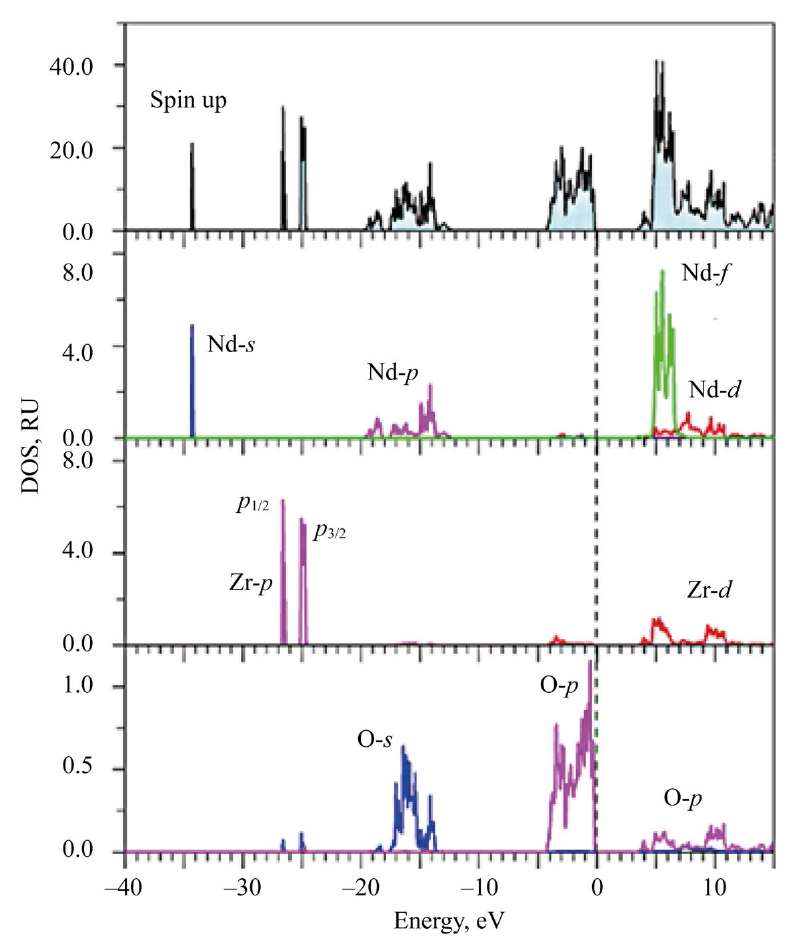
Fig. 5. Total and partial densities of states (DOS) of electrons for spin down in Nd2Zr2O7 calculated in GGA–PBE+U+SOC approximation
In regions 2, 12–18 eV from Ev in XPS, there is also a broad peak with features B1, B2 and C for La2Zr2O7 and B for Nd2Zr2O7. The theoretical calculation shows the entire fine structure that forms the peak in XPS. 5p⁶-states of La and Nd are split into 5p1/2- and 5p3/2-states. This splitting is already evident in free atoms La and Nd [25].
The spin-orbit splitting in a free atom is also present in a solid (Fig. 2) in the third panel from the bottom for the partial states of La. It is the spin-orbit splitting of the 5p-states of La that leads to the splitting of the 2s-states of oxygen. This is clearly seen in the very bottom panel of Figure 2, where the partial states of oxygen are shown. As Figure 2 shows, in the energy region ~12–18 eV, the deep-lying 5p-states of La interact with the 2s-states of oxygen. This interaction of deep-lying states in a solid is unusual and is related primarily to:
- spin-orbit splitting of the 5p-states of La;
- the fact that the 2s-wave function of oxygen is spatially and energetically strongly stretched.
The presence of structural elements B1, B2 and С in the X-ray photoelectron spectrum coincides well with the calculations of the peak in the partial densities of the electron states of La and O.
The third energy region (from 24 to 27 eV) from Ev — peaks D1 and D2 in the X-ray photoelectron spectrum of La2Zr2O7, С — in the spectrum of Nd2Zr2O7. This region corresponds to the 4p-states of Zr, which are split in the atom into:
- 4p1/2-state with energy 35 eV (N2);
- 4p3/2-states with energy 33 eV (N3).
In the XPS curve of La2Zr2O7, the splitting of the 4p-states of Zr is manifested as an asymmetry of the lines with elements D1 and D2.
The deepest states of the valence bands of La2Zr2O7 and Nd2Zr2O7 are already semi-core states. The fourth energy region in the XPS spectrum (small peak E in Fig. 2, 3) is the 5s-states of La and Nd. Note that La 5s-state in La2Zr2O7 is not split compared to the 5s-states of Nd with different spin directions (Fig. 3). The splitting of the 5s-states of Nd for spin up and spin down occurs under the action of the internal magnetic field. It is created by four 4f-electrons, which are aligned identically with spin up according to Hund's rule [26]. The broad influx of D in the XPS spectrum (Fig. 3) corresponds to the 5s-states of Nd.
The energy distribution of the electron states in the valence band La2Zr2O7 correlates well with the electronegativity (EN) values of the elements [27] included in this compound (Table 2).
Table 2
Electronegativity of Elements Included in the Compounds under Study [27]
|
Element |
O |
Zr |
La |
Nd |
Sm |
Eu |
Gd |
|
EN |
3.44 |
1.33 |
1.10 |
1.14 |
1.17 |
1.20 |
1.20 |
Thus, oxygen has the highest EN (3.44), therefore, it is quite natural that the upper part of the valence band is formed by the 2p-state of O. The admixture of the 4d- and 5s-states of Zr to the 2p-states of oxygen is insignificant, since the Zr-O1 bond is predominantly ionic in nature. The electronegativity of oxygen (EN = 3.44) is significantly higher than that of Zr (EN = 1.33). Due to this, the 4d- and 5s-electron densities of Zr are apparently attracted to the oxygen atom (O1), which is typical for the octahedral environment of the Zr atom by О1 atoms. There are also six О1 atoms in the environment of the La atom. The electronegativity of La (EN = 1.1) is significantly less than ENS = 3.44. Admixture of 5d- and 6s-states of La is almost not observed. The bond between La and О1 atoms is predominantly ionic in nature, the share of covalence in this bond is very small.
The bottom of the conduction band in both compounds is formed mainly by unoccupied f- and d-states of La/Nd, as well as d-states of Zr (Fig. 2, 4, 5).
A well-known problem of calculations using the exchange-correlation potential in the GGA-approximation is the underestimation of the obtained value of the band gap. For some non-conducting compounds, the calculations even give a conducting state or, as in the case of Nd2Zr2O7 in this calculation, a zero value of the band gap. Taking into account the strong interaction of f- electrons in Nd atom, e.g., within the framework of the LDA+U (or GGA+U) approximation in the EES calculations of Nd2Zr2O7, leads to the appearance of a small forbidden band, but the value close to the experimental one can be obtained either in calculation schemes that consider multi-electron phenomena, or by using hybrid or metapotentials, such as the modified Becke-Johnson potential (mBJ) [28].
Table 3 gives the values of the widths of the forbidden bands Eg. They were calculated taking into account the spin-orbit splitting (SOC) of the electron states in the La and Nd atoms in the GGA–PBE approximations for La2Zr2O7 (GGA–PBE+SOC) and GGA+PBE+U+SOC (with U = 5eV for 4f-states of Nd) for Nd2Zr2O7.
Table 3
Calculated Values of the Widths of Prohibited Bands Eg
|
Compound |
Exchange-correlation potential |
Eg, eV |
|
La2Zr2O7 |
GGA–PBE+SOC |
3.928 |
|
Nd2Zr2O7 |
GGA–PBE+U+SOC |
3.393 |
The complex dielectric function ε(ω) = ε1(ω) + iε2(ω) — the most important characteristic for calculating the optical response of materials to electromagnetic impact. The dielectric function, in principle, should include both transitions between bands and transitions within a band. Interband transitions are divided into direct and indirect. In these calculations, two factors are ignored. The first is intraband transitions, since they are important for metals, and the compounds under study are semiconductors. The second is the contribution of phonons and other quasiparticles included in indirect interband transitions. Only direct transitions between occupied and unoccupied states are considered. The cubic symmetry of the pyrochlore crystal structure determines only three non-zero (diagonal) elements of the dielectric tensor, and the values of all three of these elements are the same.
The calculated curves of the actual ɛ1(ω) and imaginary ɛ2(ω) parts of the permittivity for La2Zr2O7 and Nd2Zr2O7 are shown in Figure 6.
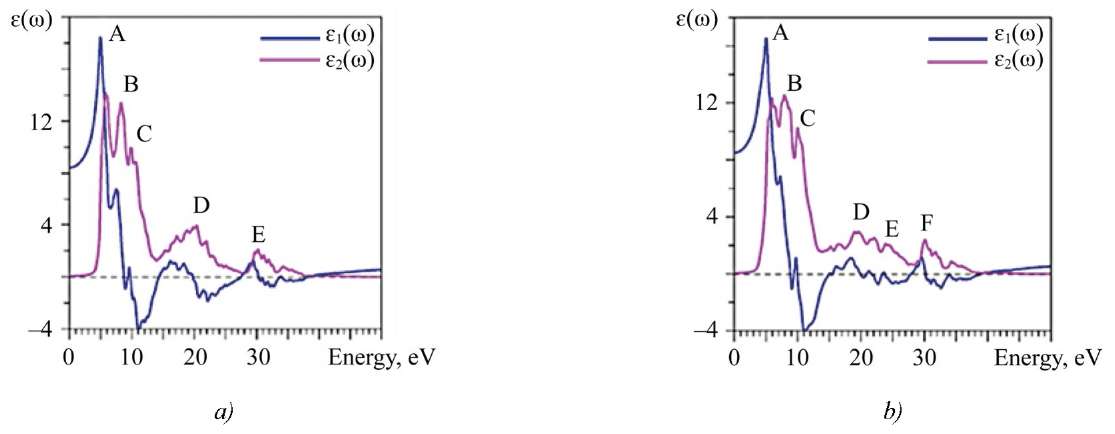
Fig. 6. Calculated actual (ε1) and imaginary parts of permittivity: a — La2Zr2O7; b — Nd2Zr2O7
The spectral peaks of the absorbing part of the dielectric function correspond to the allowed dipole transitions between the valence band and the conduction band. To identify the fine structure elements, it is required to compare the values of the optical matrix elements. The observed structures correspond to those transitions that have large values of the optical matrix dipole transition elements. When calculating ɛ2(ω), only dipole transitions within the atom, i.e., without crossover transitions, were taken into account. The interpretation of peaks A, B, C, D, E, F in Figure 6 for ɛ2(ω) is given in Table 4.
Table 4
Interpretation of Major Peaks ɛ2(ω)
|
Compound |
Peak |
Energy, eV |
Atom |
Transition |
|
La2Zr2O7 |
A |
≈ 5 |
O |
p → s(d) |
|
B |
≈ 8 |
O |
p → s |
|
|
C |
≈ 10 |
O |
p → s |
|
|
D |
≈ 20 |
O La |
p → s 5p → d |
|
|
E |
≈ 30 |
Zr |
4p → d |
|
|
Nd2Zr2O7 |
A |
5.07 |
O |
p → s |
|
B |
7.8 |
O |
p → s |
|
|
C |
10.2 |
O |
p → s |
|
|
D E |
19.09 24.02 |
O Nd |
p → s 5p → d |
|
|
F |
30.11 |
Zr |
4p → d |
Figure 6 shows the process when electrons of p-symmetry in the upper part of the valence band (peak А in XPS) pass to states of s- and d-symmetry in the conduction band of the oxygen atom. This is how the highest peak of the curve of the imaginary part of the dielectric function ɛ2(ω) is formed, covering the range 5–8 eV.
The second and third highest peaks of the curve ɛ2(ω) — B and C with energies 8.28 and 9.86 eV, respectively. They are caused by transitions of oxygen valence p- electrons to free states of oxygen s-symmetry. Let us consider the wide maximum D on the curve ɛ2(ω). The “picket-fence” of small additional peaks appeared due to transitions of oxygen s-symmetry electrons to free states of oxygen p-symmetry. In addition, in peak D (energy ̴ 20 eVВ), there is a contribution from the transitions of the valence 5p-electrons of La to the vacant d-states of La in the conduction band. Finally, small peak Е (energy ̴ 30 eV) corresponds to the transition of the valence 4p-electrons of Zr to the unoccupied d-states of Zr. At zero energy, the calculated value ɛ2(0) for La2Zr2O7 is 8.4334, and for Nd2Zr2O7 — 8.501.
All other optical properties can be derived from ɛ1(ω) and ɛ2(ω). These include, for example: absorption coefficient α(ω), refractive index n(ω), extinction coefficient k(ω), optical reflectivity R(ω), and energy loss spectrum L(ω) [28].
The high optical absorption coefficient α(ω) ˃ 10⁵ cm⁻¹ [29] is recorded in three clearly defined regions: from 5 to 14 eV, from 14 to 28 eV and from 28 to 40 eV (Fig. 7). Apparently, such absorption may indicate the potential of using thin-film elements from La2Zr2O7 and Nd2Zr2O7.
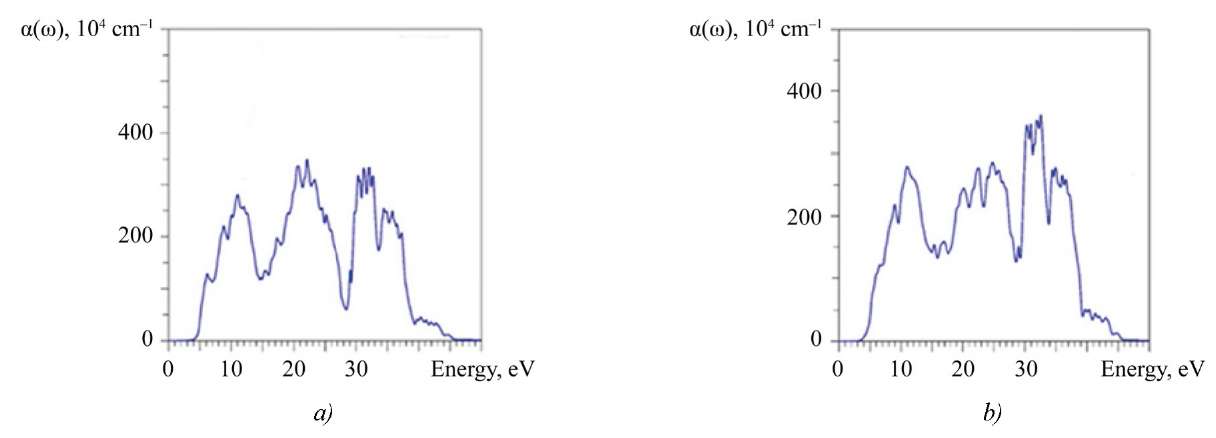
Fig. 7. Calculated absorption coefficient α(ω): a — La2Zr2O7; b — Nd2Zr2O7
In addition, the optical absorption spectrum is characterized by a large number of peaks. They are formed due to transitions between occupied levels of the valence band and free levels of the conduction band, allowed by the selection rules (Δl ≠ 0) and related to one atom (cross-transitions between neighboring atoms are unlikely). Such a picket-fence of small peaks on the curve а(ɷ) is undoubtedly related to the features of the above-described electron-energy structure of La2Zr2O7 and Nd2Zr2O7. Probably, it should be taken into account when using these compounds in optoelectronics.
The complex refractive index N(ω) = n(ω) + ik(ω) can be obtained from the complex dielectric function ɛ(ω), where the refractive index n(ω) depends mainly on the actual part ɛ1(ω), and the extinction coefficient k(ω) depends on the imaginary part of the dielectric function ɛ2(ω) [30].
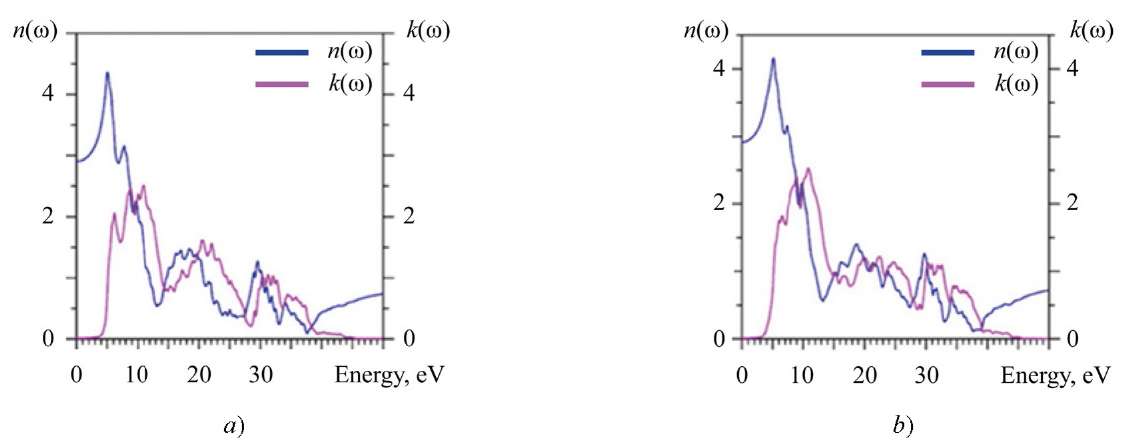
Fig. 8. Calculated refractive index n(ω) and extinction coefficient k(ω): a — La2Zr2O7; b — Nd2Zr2O7
At zero energy, the calculated value n(0) (static refractive index) for La2Zr2O7 is 2.904, and for Nd2Zr2O7 — 2.916.
The extinction coefficient k(ω), responsible for the absorption of the electromagnetic wave incident on the crystal, is obtained from the imaginary part of the dielectric function ɛ2(ω) (Fig. 6). Therefore, there are also three regions where value k(ω) increases from 5 to 13 eV, from 14 to 28 eV and from 28 to 40 eV. The attenuation of the intensity, represented by the extinction coefficient k(ω), starts with a decrease in the function n(ω) (Figс. 8). La2Zr2O7 and Nd2Zr2O7 crystals can absorb photons in a wide energy range (4–10 eV).
In general, the extinction coefficient of La2Zr2O7 and Nd2Zr2O7 is not isotropic and has three well-defined regions (energies are given above) where isotropic behavior of k(ω) is not observed. In these regions, the difference in k(ω) values is 25–50%.
The reflection coefficient R(ω) is shown in Figure 9. The spectrum R(ω) consists of three clearly defined energy regions. The same feature was noted for other optical characteristics. At zero energy, the calculated value R(0) for La2Zr2O7 is 23.786%, and for Nd2Zr2O7 — 23.935%.
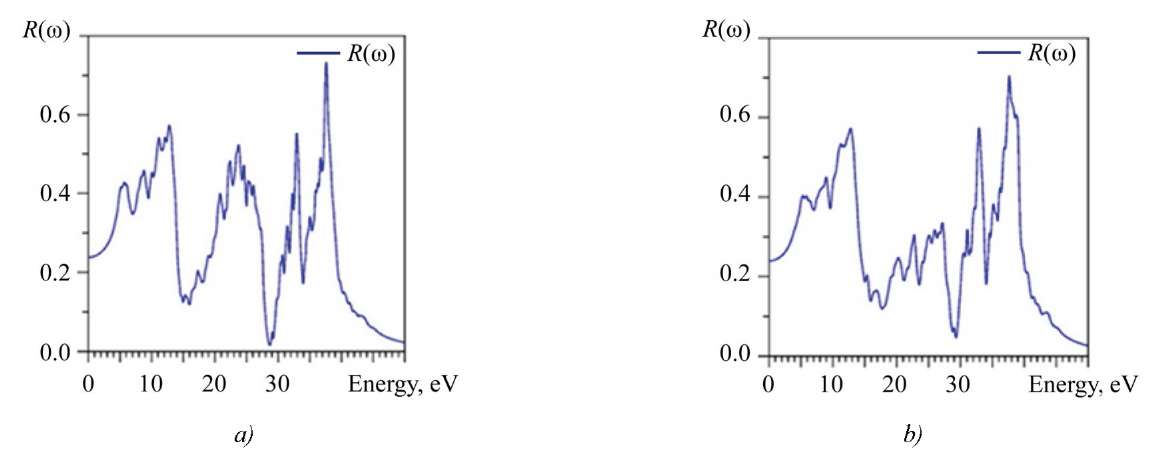
Fig. 9. Calculated reflection coefficient R(ω): a — La2Zr2O7; b — Nd2Zr2O7
It is evident from Figure 8 that incident photons with energy lower than the energy of the forbidden gap (̴ 4 eV) are not absorbed. Photons with energy from 4 eV to ̴ 40 eV are absorbed by La2Zr2O7, Nd2Zr2O7 crystals and excite electrons in the conduction band, while positively charged holes are formed in the valence band. However, part of the photon energy will be lost during thermalization, and it is reflected in the electron energy loss spectrum L(ω) shown in Figure 10.
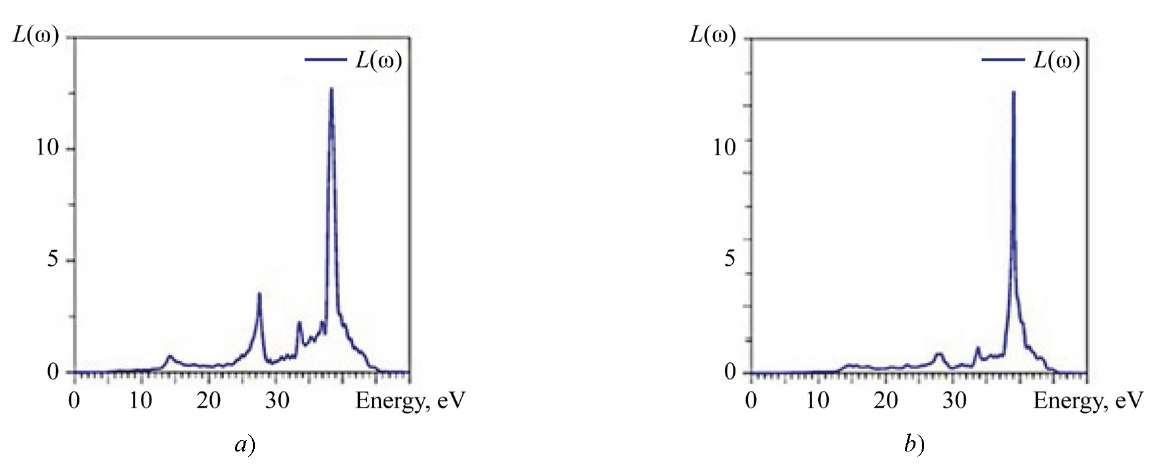
Fig. 10. Calculated spectrum of electron energy losses: a — La2Zr2O7; b — Nd2Zr2O7
The energy loss of the electron becomes significant at 14 eV (small peak), ̴ 27 eV, ̴ 33.5 eV. The largest value L(ω) is reached at 39 eV, which corresponds to a sharply decreasing edge of the absorption coefficient а(ɷ) (Fig. 7).
Discussion and Conclusion. The calculation of the electron density states of the valence bands of La2Zr2O7, Nd2Zr2O7 gave two results:
- allowed us to explain all the main features of the experimental X-ray photoelectron spectra of these compounds in the energy range of ~35 eV from the top of the valence band;
- showed which electron symmetry determined the main features of the experimental spectra.
Together with the obtained densities of unoccupied states, the calculated densities of occupied states allowed us to define the optical coefficients of the compounds studied. It is extremely important to take into account the corrections in the exchange-correlation part of the potential (GGA+U, mBJ). Only with them it is possible to obtain the values of the widths of the forbidden bands that correspond to the experimental data. For Nd2Zr2O7, calculations without corrections generally show a non-zero density of states at the Fermi level.
References
1. Chartier A, Meis C, Crocombette J, Corrales LR, Weber WJ. Atomistic Modeling of Displacement Cascades in La2Zr2O7 Pyrochlore. Physical Review B. 2003;67:174102. https://doi.org/10.1103/PhysRevB.67.174102
2. Stanek CR, Minervini L, Grimes RW. Nonstoichiometry in A2B2O7 Pyrochlores. Journal of the American Ceramic Society. 2002;85(11):2792–2798. https://doi.org/10.1111/j.1151-2916.2002.tb00530.x
3. Pirzada M, Grimes RW, Minervini L, Maguire JF, Sickafus KE. Oxygen Migration in A2B2O7 Pyrochlores. Solid State Ionics. 2001;140:201–208. https://doi.org/10.1016/S0167-2738(00)00836-5
4. Tabira Y, Withers RL, Minervini L, Grimes RW. Systematic Structural Change in Selected Rare Earth Oxide Pyrochlores as Determined by Wide-Angle CBED and a Comparison with the Results of Atomistic Computer Simulation. Journal of Solid State Chemistry. 2000;153(1):16–25. https://doi.org/10.1006/jssc.2000.8712
5. Helean KB, Ushakov SV, Brown CE, Navrotsky A, Lian J, Ewing RC, et al. Formation Enthalpies of Rare Earth Titanate Pyrochlores. Journal of Solid State Chemistry. 2004;177(6):1852–1866. https://doi.org/10.1016/j.jssc.2004.01.009
6. Lian J, Zu XT, Kutty KVG, Chen J, Wang LM, Ewing RC. Ion-Irradiation-Induced Amorphization of La2Zr2O7 Pyrochlore. Physical Review B. 2002;66:054108. https://doi.org/10.1103/PhysRevB.66.054108
7. Chen J, Lian J, Wang LM, Ewing RC, Wang RG, Pan W. X-ray Photoelectron Spectroscopy Study of Disordering in Gd2(Ti1-xZrx)2O7 Pyrochlores. Physical Review Letters. 2002;88:105901. https://doi.org/10.1103/PhysRevLett.88.105901
8. Yong Jiang, Smith JR, Odette GR. Prediction of Structural, Electronic and Elastic Properties of Y2Ti2O7 and Y2TiO5. Acta Materialia. 2010;58(5):1536–1543. https://doi.org/10.1016/j.actamat.2009.10.061
9. Winter MR, Clarke DR. Thermal Conductivity of Yttria-Stabilized Zirconia-Hafnia Solid Solutions. Acta Materialia. 2006;54(19):5051–5059. https://doi.org/10.1016/j.actamat.2006.06.038
10. Matteucci F, Cruciani G, Dondi M, Baldi G, Barzanti A. Crystal Structural and Optical Properties of Cr-Doped Y2Ti2O7 and Y2Sn2O7 Pyrochlores. Acta Materialia. 2007;55(7):2229–2238. https://doi.org/10.1016/j.actamat.2006.11.008
11. Uno M, Kosuga A, Okui M, Horisaka K, Muta H, Kurosaki K, et al. Photoelectrochemical Study of Lanthanide Zirconium Oxides, Ln2Zr2O7 (Ln = La, Ce, Nd and Sm). Journal of Alloys and Compounds. 2006;420:291–297. https://doi.org/10.1016/j.jallcom.2005.10.072
12. Ciomaga Hatnean M, Lees MR, Balakrishnan G. Growth of Single-Crystals of Rare-Earth Zirconate Pyrochlores, Ln2Zr2O7 (with Ln = La, Nd, Sm, and Gd) by the Floating Zone Technique. Journal of Crystal Growth. 2015;418:1–6. https://doi.org/10.1016/j.jcrysgro.2015.01.037
13. Feng J, Xiao B, Wan CL, Qu ZX, Huang ZC, Chen JC, et al. Electronic Structure, Mechanical Properties and Thermal Conductivity of Ln2Zr2O7 (Ln = La, Pr, Nd, Sm, Eu and Gd) Pyrochlore. Acta Materialia. 2011;59(4):1742–1760. https://doi.org/10.1016/j.actamat.2010.11.041
14. Zheng Li, Wei Pan. Electronic Structure and Transport Properties of La2Zr2O7 Pyrochlore from First Principles. Solid State Phenomena. 2018;281:767–773. https://doi.org/10.4028/www.scientific.net/SSP.281.767
15. Liu B, Wang JY, Zhou YC, Liao T, Li FZ. Theoretical Elastic Stiffness, Structure Stability and Thermal Conductivity of La2Zr2O7 Pyrochlore. Acta Materialia. 2007;55(9):2949–2957. https://doi.org/10.1016/j.actamat.2006.12.035
16. Subramanian MA, Aravamudan G, Subba Rao GV. Oxide Pyrochlores — A Review. Progress in Solid State Chemistry. 1983;15(2):55–143. https://doi.org/10.1016/0079-6786(83)90001-8
17. Blaha P, Schwarz K, Tran F, Laskowski R, Madsen GKH, Marks LD. WIEN2k: an APW+lo Program for Calculating the Properties of Solids. Journal of Chemical Physics. 2020;152(7):074101. https://doi.org/10.1063/1.5143061
18. Blöchl PE, Jepsen O, Andersen OK. Improved Tetrahedron Method for Brillouin-Zone Integrations. Physical Review B. 1994;49(23):16223–16233. https://doi.org/10.1103/PhysRevB.49.16223
19. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Physical Review Letters. 1996;77(18):3865–3868. https://doi.org/10.1103/PhysRevLett.77.3865
20. Tran F, Blaha P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Physical Review Letters. 2009;102(22):226401. https://doi.org/10.1103/PhysRevLett.102.226401
21. Anisimov VI, Solovyev IV, Korotin MA, Czyżyk MT, Sawatzky GA. Density-Functional Theory and NiO Photoemission Spectra. Physical Review B. 1993;48(23):16929–16934. https://doi.org/10.1103/PhysRevB.48.16929
22. Novák P, Boucher F, Gressier P, Blaha P, Schwarz K. Electronic Structure of the Mixed Valence System (YM)2BaNiO5 (M = Ca, Sr). Physical Review B. 2001;63(23):235114. https://doi.org/10.1103/PhysRevB.63.235114
23. Hong Jiang. Band Gaps from the Tran-Blaha Modified Becke-Johnson Approach: A Systematic Investigation. The Journal of Chemical Physics. 2013;138(13):134115. https://doi.org/10.1063/1.4798706
24. Tuan V Vu, Khyzhun OY, Lavrentyev AA, Gabrelian BV, Kalmykova KF, Isaenko LI, et al. Electronic Band Structure and Optical Properties of Li2In2GeSe6 Crystal. Materials Today Communications. 2023;35:105798. https://doi.org/10.1016/j.mtcomm.2023.105798
25. Lotz W. Electron Binding Energies in Free Atoms. The Journal of the Optical Society of America. 1970:60(2):206–210.
26. Lide DR (ed). CRS Handbook of Chemistry and Physics. 87th ed. Boca Raton; London; New York: CRC Press; Taylor & Francis; 2007. 2608 p.
27. Ambrosch-Draxl C, Sofo JO. Linear Optical Properties of Solids within the Full-Potential Linearized Augmented Planewave Method. Computer Physics Communications. 2006;175(1):1–14. https://doi.org/10.1016/j.cpc.2006.03.005
28. Khan SA, Reshak AH. Optoelectronic and Transport Properties of Zintl Phase KBa2Cd2Sb3 Compound. Computational Materials Science. 2014;95:328–336. https://doi.org/10.1016/j.commatsci.2014.07.031
29. Boujnah M, Dakir O, Zaari H, Benyoussef A, Kenz AE. Optoelectronic Response of Spinels CdX2O4 with X = (Al, Ga, In) through the Modified Becke-Johnson Functional. Journal of Applied Physics. 2014;116(12):123703. https://doi.org/10.1063/1.4896110
30. Tuan V Vu, Lavrentyev AA, Doan V Thuan, Chuong V Nguyen, Khyzhun OY, Gabrelian BV, et al. Electronic Properties and Optical Behaviors of Bulk and Monolayer ZrS2: A Theoretical Investigation. Superlattices and Microstructures. 2019;125:205–213. https://doi.org/10.1016/j.spmi.2018.11.008
About the Authors
A. A. LavrentyevRussian Federation
Anatoliy A. Lavrentyev, Dr.Sci. (Phys.-Math.), Professor, Head of the Electrical Engineering and Electronics Department
1, Gagarin Sq., Rostov-on-Don, 344003
B. V. Gabrelian
Russian Federation
Boris V. Gabrelian, Cand.Sci. (Phys.-Math.), Associate Professor of the Computer and Automated Systems Software Department
1, Gagarin Sq., Rostov-on-Don, 344003
Vu Van Tuan
Viet Nam
Vu Van Tuan, Cand.Sci. (Phys.-Math.), Leading Researcher, Laboratory of Computational Physics
69/68, Dang Thuy Tram Str. Ward 13, Binh Thanh District, Ho Chi Minh City, 70000
K. F. Kalmykova
Russian Federation
Ksenia F. Kalmykova, Teaching Assistant of the Electrical Engineering and Electronics Department
1, Gagarin Sq., Rostov-on-Don, 344003
Model calculations of the electronic structure of the compounds La2Zr2O7 and Nd2Zr2O7 are performed in the study. The densities of electronic states are obtained, and the optical characteristics of the compounds are calculated. High absorption coefficients are found in a wide energy range. The results allow us to explain the features of the experimental X-ray spectra. The study opens up new prospects in materials science and optics.
Review
For citations:
Lavrentyev A.A., Gabrelian B.V., Tuan V.V., Kalmykova K.F. Ab initio Calculations of the Electronic-Energy Structure and Optical Properties of Lanthanum and Neodymium Pyrozirconates. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):129-141. https://doi.org/10.23947/2687-1653-2025-25-2-129-141. EDN: MJOLRM
JATS XML














































