Перейти к:
Математическое моделирование оценки мощности заряда при исключении просадочности лёссов глубинными гидровзрывами
https://doi.org/10.23947/2687-1653-2025-25-3-233-241
EDN: OVUJUV
Аннотация
Введение. Просадочные лёссовые грунты, широко распространённые в России, Китае и Средней Азии, представляют собой значимую проблему в современном строительстве из-за своей склонности к просадке и низкой прочности при внешних нагрузках. Недостаточное внимание к их физико-механическим свойствам может привести к деформации сооружений, что создаёт угрозу безопасности и финансовые потери. Научные исследования в этой области являются фрагментарными и не дают достаточного понимания методов уплотнения и их влияния на долговечность конструкций. Кроме того, не существует разработанных оптимизированных математических моделей, позволяющих предсказать эффективность инженерно-технологических процессов уплотнения. Таким образом, целью данного исследования является разработка математической модели, определяющей мощность заряда взрывчатого вещества для уплотнения лёссов. Данная модель направлена на исключение экспериментального этапа, что улучшает качество уплотнения и способствует экономии финансовых ресурсов в строительстве.
Материалы и методы. Математическое моделирование проводили путём включения решения обратной прикладной задачи оценки мощности заряда взрывчатого вещества при устранении просадочности лёссов. Начальнограничные задачи с полуэмпирическим дифференциальным уравнением в частных производных, описывающим уплотнение лёсса с выбросом и без выброса грунта на поверхность строительной площадки, рассматривались путём анализа конкретных моделей и математических подходов. На основе решения этих задач с использованием аналитического метода была создана математическая модель оценки мощности заряда взрывчатого вещества. Мощность определяли численно двумя методами: расчётами в программе, разработанной на языке Python, и путём моделирования вычислительного эксперимента с оценкой погрешности результата. При этом учитывали влияние физико-механических свойств грунтов, их изотропность и анизотропность.
Результаты исследования. Построена математическая модель мощности заряда взрывчатого вещества при уплотнении просадочных лёссов с использованием глубинных гидровзрывов. Учтены плотность сухого грунта до и после уплотнения, коэффициент вертикальной диффузии, дисперсионные координатные изменения газа в уплотняемом грунте, а также глубина заложения заряда взрывчатого вещества. При средней плотности сухого уплотнённого грунта абсолютная погрешность расчётных значений мощности заряда составила 3,28 г для уплотнения лёссов без выброса и 21,13 г — для ситуации с выбросом грунта на поверхность. Показана адекватность предлагаемого математического решения экспериментальным данным натурного строительного объекта.
Обсуждение. Предложенная модель позволяет проводить оценку мощности заряда взрывчатого вещества для изотропных и анизотропных геологических систем. Полученные аналитические представления демонстрируют степень и характер влияния физико-механических свойств грунтов на величину мощности заряда. Численное сравнение как с экспериментальными данными натурного уплотнения грунтов, так и с рекомендациями по уплотнению просадочных грунтов большой мощности гидровзрывным методом показало, что предложенная математическая модель согласуется с эмпирическими данными.
Заключение. Основным результатом исследования является математическая модель мощности заряда взрывчатого вещества при устранении просадочности лёссов глубинными гидровзрывами. Построены аналитические представления мощности заряда с учётом физико-механических свойств грунтов. Получена численная оценка мощности, согласующаяся со значениями эмпирических данных. Практическая значимость исследования состоит в возможности применения математической модели в качестве расчётной методики и внедрения в исследовательские и проектные организации. Дальнейшие исследования будут направлены на построение решений средствами математического моделирования и других обратных задач в рамках инженерно-технологического процесса уплотнения грунтов.
Ключевые слова
Для цитирования:
Тарасенко Е.О. Математическое моделирование оценки мощности заряда при исключении просадочности лёссов глубинными гидровзрывами. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):233-241. https://doi.org/10.23947/2687-1653-2025-25-3-233-241. EDN: OVUJUV
For citation:
Tarasenko E.O. Mathematical Modeling of Charge Power Assessment with Exclusion of Loess Subsidence by Deep Hydraulic Blasts. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):233-241. https://doi.org/10.23947/2687-1653-2025-25-3-233-241. EDN: OVUJUV
Введение. Исследование поверхности земной коры показало распространение структурно неустойчивых просадочных лёссовых грунтов по всему миру. Преобладают они в России [1], Китае [2] и Средней Азии [3]. Лёссами покрыто около 17 % территории России. Наиболее часто лёссовые грунты встречаются на Северном Кавказе, юге России, в Крыму и на других территориях.
В планетарном масштабе лёсс представляет собой горную породу четвертичного периода. Ему характерны жёлтые, жёлто-коричневые или жёлто-палевые цвета [4]. Лёссы имеют низкую плотность и высокую макропористость, что позволяет воде глубоко проникать в структуру грунта. Это приводит к быстрому размоканию [5] и просадкам [6]. Рассчитанные просадки от собственного веса достигают значений 2,5 м [7].
Возведение безопасных и прочных зданий и сооружений на просадочных грунтах не представляется возможным. Проектирование и строительство объектов на лёссах, а также недостаточное исследование их физико-механических свойств приводят к деформациям зданий и сооружений, снижая срок их безопасной эксплуатации. Как следствие, увеличиваются финансовые затраты и стремительно возрастает угроза безопасности.
Устранение просадочности осуществляется различными методами, выбор которых зависит от условий их реализации. В данной работе рассматривается метод уплотнения лёссов глубинными гидровзрывами, показывающий экономическую эффективность при низких производственных затратах [8].
Инженерно-технологический процесс уплотнения осуществляется на основе всестороннего детального исследования физико-механических свойств просадочных лёссовых грунтов, которые широко представлены в современной литературе. Проведены исследования проницаемости просадочных грунтов [9], деформационных характеристик лёсса [10] с различной влажностью, энергии уплотнения [11], ползучести [12] и механической устойчивости глин [13]. Прочностные и деформационные свойства глинистых грунтов с точки зрения физико-химической теории проанализированы под действием внешних нагрузок, сжимающей нагрузки, противодавления [14]. Однако математическое описание физико-механических свойств просадочных глин и суглинков, а также их изменения в результате уплотнения глубинными взрывами в отмеченных работах не проведено. Исследования осуществляются на основе полевых и компрессионных испытаний лёссовых грунтов.
Математизация отдельных свойств уплотняемых взрывом грунтов, а именно их прочностных характеристик, приведена в отчётах об инженерно-геологических изысканиях [15]. Реализована адаптация прочностных показателей к значениям для численных расчётов. Исследования показателей удельного сцепления и угла внутреннего трения уплотняемых глубинными взрывами грунтов методом регрессионного анализа проводятся в [16]. Реализовано моделирование коэффициента вертикальной диффузии газа в лёссовых грунтах, уплотняемых взрывом [17]. Построены регрессионные модели отдельных физических параметров грунтов, таких как пористость, проницаемость, водонасыщенность [18], фильтрация в зависимости от давления [19]. Эти исследования позволяют оценить физико-механические свойства лёссовых грунтов после их уплотнения глубинными взрывами, но не описывают особенности реализации инженерно-технологического процесса уплотнения лёссов.
Математическое моделирование уплотнения лёссовых грунтов глубинными гидровзрывами требует решения отдельных обратных прикладных задач — оценки мощности заряда взрывчатого вещества, глубины его заложения, дисперсионных координатных изменений атомов газа, образуемого при взрыве, в грунтах и другие. Одна из этих задач задаёт цель статьи — математическое моделирование мощности заряда взрывчатого вещества с учётом физико-механических свойств уплотняемых геологических систем, их анизотропности и изотропности.
Создание модели позволит не только улучшить качество уплотнения, но и сократить финансовые затраты на реализацию инженерно-технологического процесса. Уплотнение лёсса с использованием предложенной модели исключает этап пробных предварительных взрывов на строительной площадке, который проводится для определения оптимальной мощности заряда взрывчатого вещества и достижения требуемых механических свойств непросадочных грунтов.
Достижение цели исследования реализуется на основе применения инструментария математического моделирования (аналитически и численно). Будут построены аналитические представления для оценки мощности заряда взрывчатого вещества, исходя из решения начально-граничных задач с полуэмпирическим уравнением диффузии. Учтутся физико-механические свойства уплотняемых грунтов. Для получения оценки мощности заряда будут применены средства численного моделирования. Проведение вычислительного эксперимента позволит установить адекватность предлагаемого решения обратной задачи экспериментальным данным.
Материалы и методы. Обратная задача оценки мощности заряда взрывчатого вещества возникает в рамках математического моделирования уплотнения просадочных грунтов глубинными взрывами. Процесс уплотнения лёссов с целью устранения их просадочности описывается моделью, основанной на заданном дифференциальном полуэмпирическом уравнении диффузии, а также с учетом начальных и граничных условий. Математическая постановка плотностной модели уплотняемых грунтов имеет вид [17]:
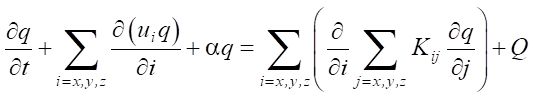 , (1)
, (1)
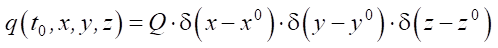 , (2)
, (2)
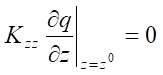 ,
, 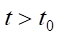 , (3)
, (3)
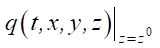 ,
, 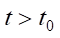 , (4)
, (4)
здесь q(t, x, y, z) — плотность уплотнённого грунта при глубинном взрыве в момент времени t; u — параметр горизонтального распространения газа; Kxx, Kyy, Kzz — коэффициенты диффузии; α — параметр взаимодействия газа, появившегося в результате взрыва, и лёссового просадочного грунта; Q — мощность заряда взрывчатого вещества (т.е. количество газа, выброшенного зарядом в момент времени t0 в точке x0, y0, z0); δ — дельта-функция Дирака.
Начально-граничная задача (1)–(3) соответствует процессу уплотнения лёсса глубинными взрывами с выбросом грунта на поверхность. Задача (1), (2), (4) — уплотнение лёсса без выброса на поверхность. Аналитические решения задач (1)–(3) и (1), (2), (4) представимы, соответственно, в виде [17]:
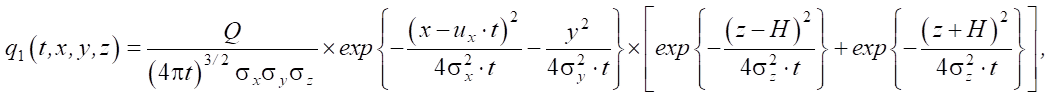 (5)
(5)
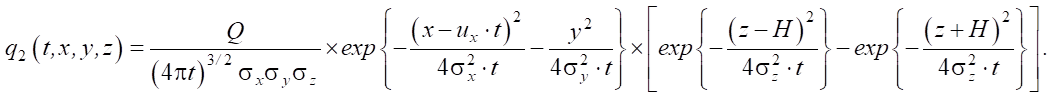 (6)
(6)
В решениях (5) и (6) (0, 0, H) — координаты расположения сосредоточенного заряда взрывчатого вещества с мощностью Q = const > 0, действующего в момент времени t0; Н — глубина заложения заряда взрывчатого вещества; 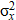 ,
, 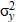 ,
, 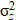 — дисперсионные изменения координат атомов газа в грунте.
— дисперсионные изменения координат атомов газа в грунте.
Постановка обратной задачи об оценке мощности заряда взрывчатого вещества: пусть установлены средние значения плотности грунта q1 и q2 уплотнённого методом глубинного взрыва зарядов взрывчатого вещества, соответствующие соотношениям (5) и (6) для случаев уплотнения грунтов с выбросом и без выброса на поверхность; известно значение глубины расположения заряда взрывчатого вещества Н; определена величина дисперсионных координатных изменений атомов газа в грунте σ. Требуется оценить мощность заряда взрывчатого вещества Q.
Результаты исследования. Решения обратных прикладных задач об оценке мощности заряда при уплотнении просадочных лёссов глубинными гидровзрывами реализуем на основе аналитического и численного методов математического моделирования.
Согласно (5) и (6) возможны два случая: уплотнение с выбросом на поверхность и без выброса. В первом случае на основе (5) получим уравнение:
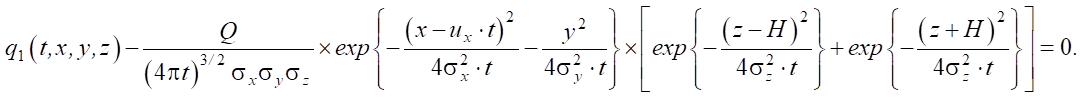 (7)
(7)
Во втором случае на основе (6) приходим к уравнению:
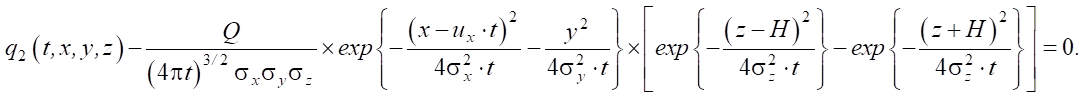 (8)
(8)
Для геологических систем характерными физико-механическими свойствами являются анизотропность и изотропность.
Если исследуемая геологическая система является анизотропной, то фильтрационные свойства грунта зависят от направления движения грунтовой воды. При реализации уплотнения грунтов взрывами с поверхностным выбросом искомый корень Q уравнения (7) примет аналитическое представление:
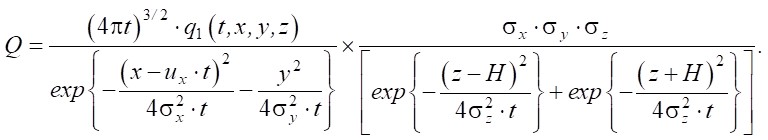 (9)
(9)
Если исследуемая система является изотропной, тогда фильтрационные свойства грунта не зависят от направления движения грунтовой воды. Предположим, что дисперсионные координатные изменения равны по всем направлениям σz = σy = σx, тогда при уплотнении грунтов с выбросом на поверхность искомый корень Q уравнения (7) примет аналитическое представление:
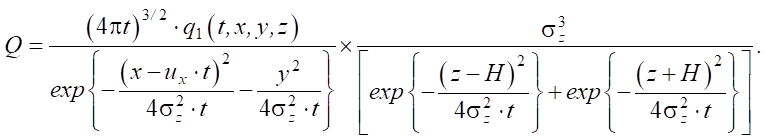 (10)
(10)
Теперь рассмотрим случай уплотнения грунта глубинными взрывами без выброса на поверхность. Если рассматриваемая геологическая система является анизотропной, то искомый корень Q уравнения (8) примет аналитический вид:
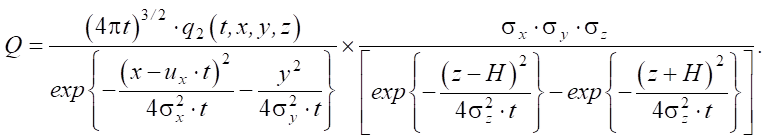 (11)
(11)
Если рассматриваемая система является изотропной, то σz = σy = σx и тогда искомый корень Q уравнения (8) запишем в виде:
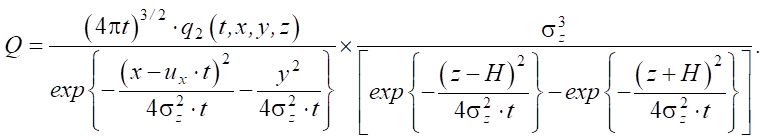 (12)
(12)
Построенные соотношения (9)–(12) аналитически задают мощность заряда взрывчатого вещества в зависимости от физико-механических свойств уплотняемых грунтов и глубины заложения заряда. Для оценки значений мощности применим средства численного моделирования.
Вычислительный эксперимент. Проведём вычислительный эксперимент по решению обратных задач, возникающих при математическом моделировании уплотнения лёссов глубинными взрывами с целью численной оценки мощности заряда взрывчатого вещества. Расчёты будут основаны на данных натурного строительного объекта.
На строительном объекте «Строительство товарно-сырьевого склада СУГ ООО «Ставролен» (г. Будённовск) проведено уплотнение глубинными взрывами просадочных грунтов [8], мощность которых равна 28 м. Суммарная просадка грунта под собственным весом составила от 43 до 78 см. На глубине 29–31 м были зафиксированы грунтовые воды [20]. Средняя плотность сухого грунта до уплотнения равнялась 1,43 г/см³.
На строительной площадке для проведения уплотнения пробурили дренажно-взрывные скважины диаметром 20 см по сетке см. В них поместили на глубину H = 600 см заряды водостойкого аммонита массой по 10 000 г. Через месяц после уплотнения было выполнено бурение контрольных скважин с отбором монолитов. Плотность сухого грунта приняла значения в интервале от 1,60 г/см³ до 1,75 г/см³. Средняя плотность сухого уплотнённого грунта составила 1,66 г/см³ [8]. Лёсс относится к грунтам со столбчатой структурой и является ортотропным в вертикальном направлении [20]. Учитывая физические показатели грунта, рассчитаем коэффициент вертикальной диффузии газа в грунте Kz, согласно [17]. По Kz определим дисперсионные координатные изменения атомов газа в грунте, которые равны σz = 0,726. Параметр горизонтального распространения газа равен нулю ux = 0. Расчёт значений мощности заряда взрывчатого вещества будет произведён по формуле (12). Уплотнение лёсса реализовано без выброса грунта на поверхность.
В таблице 1 представлен результат оценки мощности заряда взрывчатого вещества при известных значениях плотности уплотнённого грунта, дисперсионных координатных изменениях атомов газа в грунте и глубине заложения заряда. Расчёты проводились с использованием авторской программы, разработанной на языке программирования высокого уровня Python, предназначенной для расчёта мощности заряда взрывчатого вещества.
Таблица 1
Расчётная мощность заряда взрывчатого вещества при различных значениях плотности уплотнённого грунта без выброса на поверхность
|
Плотность грунта, г/см³ |
Расчётная мощность заряда, г |
|
1,60 |
9 797,53 |
|
1,61 |
9 809,56 |
|
1,62 |
9 815,83 |
|
1,63 |
9 836,05 |
|
1,64 |
9 876,28 |
|
1,65 |
9 936,51 |
|
1,66 |
9 996,72 |
|
1,67 |
10 046,74 |
|
1,68 |
10 094,16 |
|
1,69 |
10 114,28 |
|
1,70 |
10 137,53 |
|
1,71 |
10 159,82 |
|
1,72 |
10 186,04 |
|
1,73 |
10 208,27 |
|
1,74 |
10 228,49 |
|
1,75 |
10 243,71 |
Проведём анализ результатов, представленных в таблице 1. Для исключения свойства просадочности и достижения плотности сухого уплотнённого грунта значения ≥1,60 г/см³ мощность заряда взрывчатого вещества может принимать значения в интервале от 9 797,53 до 10 243,71 г. Согласно экспериментальным данным, мощность заряда взрывчатого вещества равна 10 000 г [8]. Абсолютная погрешность вычислений для значений плотности грунта от 1,60 г/см³ до 1,75 г/см³ не превышает значения 0,244. При средней плотности грунта q = 1,66 г/см³ абсолютная погрешность равна 3,28 г.
Рассмотрим уплотнение лёсса с выбросом грунта на поверхность. Расчёт значений мощности заряда взрывчатого вещества произведём по формуле (10) при σz = 0,726 и плотности сухого грунта от 1,60 г/см³ до 1,75 г/см³. Полученные результаты представлены в таблице 2.
Таблица 2
Расчётная мощность заряда взрывчатого вещества при различных значениях плотности уплотнённого грунта с выбросом на поверхность
|
Плотность грунта, г/см³ |
Расчётная мощность заряда, г |
|
1,60 |
9 852,18 |
|
1,61 |
9 881,62 |
|
1,62 |
9 952,77 |
|
1,63 |
10 021,13 |
|
1,64 |
10 053,84 |
|
1,65 |
10 094,28 |
|
1,66 |
10 123,92 |
|
1,67 |
10 157,54 |
|
1,68 |
10 187,62 |
|
1,69 |
10 204,75 |
|
1,70 |
10 221,83 |
|
1,71 |
10 242,25 |
|
1,72 |
10 256,89 |
|
1,73 |
10 279,34 |
|
1,74 |
10 293,79 |
|
1,75 |
10 301,24 |
Анализ значений мощности заряда взрывчатого вещества, представленных в таблице 2, показал, что расчётная мощность заряда может принимать значения от 9 852,18 г до 10 301,24 г. Абсолютная погрешность вычислений не превышает 0,301. При средней плотности грунта q = 1,66 г/см³ абсолютная погрешность равна 123,92 г. Минимальная абсолютная погрешность 0,02113 при q = 1,63 г/см³.
На рис. 1, 2 приведена графическая интерпретация расчётных значений мощности заряда взрывчатого вещества при различных показателях плотности сухого уплотнённого грунта и экспериментальных данных о мощности заряда. Отмечены значения мощности заряда в соответствии с рекомендациями по уплотнению просадочных грунтов большой мощности гидровзрывным методом1 (сплошная линия). При заложении заряда взрывчатого вещества на указанную глубину его мощность равна 9 960 г. На рис. 1 представлен случай уплотнения лёсса глубинным взрывом без выброса на поверхность. На рис. 2 — с выбросом на поверхность.

Рис. 1. Расчётная и экспериментальная мощность заряда взрывчатого вещества при различных значениях плотности грунта без выброса на поверхность

Рис. 2. Расчётная и экспериментальная мощность заряда взрывчатого вещества при различных значениях плотности грунта с выбросом на поверхность
По окончании проведения инженерно-технологического процесса уплотнения лёссов глубинными взрывами, в соответствии с [8], после сброса воды из котлована верхние буферные слои строительной площадки доуплотняются поверхностными методами.
Обсуждение. Построенная математическая модель мощности заряда взрывчатого вещества описана аналитически (9)–(12). Модель предназначена для проведения численных расчётов и оценки значений мощности заряда. Формулы показывают характер и степень зависимости мощности заряда и физико-механических свойств грунтов, их изотропности и анизотропности. Увеличение мощности заряда влечёт рост плотности грунта, снижение просадочности и пористости.
Полученные представления позволили провести теоретический эксперимент по численной оценке значений мощности заряда взрывчатого вещества. Расчётные значения имеют абсолютную вычислительную погрешность в интервалах (3,28; 243,71) г — уплотнение без выброса грунта на поверхность и (21,13; 301,24) г — уплотнение с выбросом грунта на поверхность строительной площадки.
Недостатком предложенного подхода является то, что плотность уплотняемого лёсса, величина дисперсионных координатных изменений атомов газа в грунте определяются на основе полевых и лабораторных испытаний. Глубина расположения заряда взрывчатого вещества также указывается заранее. Таким образом, при оценке мощности заряда будут содержаться штамповые и компрессионные данные. Предложенная модель учитывает изотропность и анизотропность грунтов. Полученные в настоящем исследовании результаты адекватны экспериментальным данным и подтверждают возможность их практического применения при планировании инженерно-технологического процесса уплотнения просадочных грунтов глубинными гидровзрывами.
Заключение. Основным результатом исследования является математическая модель оценки мощности заряда взрывчатого вещества. Получены аналитические выражения мощности заряда. Учтены физико-механические свойства грунтов, их изотропность и анизотропность. Численно значения мощности найдены с использованием программы, разработанной в Python. Полученные результаты хорошо согласуются со значениями натурного эксперимента и рекомендуемыми значениями, основанными на эмпирических данных.
Практическая значимость исследования состоит в возможности применения математической модели в качестве расчётной методики в исследовательских и проектных организациях, занимающихся теоретическим исследованием и практической реализацией уплотнения просадочных лёссовых грунтов. Дальнейшие исследования будут направлены на построение решений средствами математического моделирования и других обратных задач в рамках инженерно-технологического процесса уплотнения грунтов.
1. Рекомендации по уплотнению просадочных грунтов большой мощности гидровзрывным методом. Москва: Стройиздат, 1984. 56 с. URL: https://meganorm.ru/Data2/1/4293782/4293782665.pdf (дата обращения: 01.06.2025).
Список литературы
1. Трофимов В.Т. (ред.), Балыкова С.Д., Андреева Т.В., Ершова А.В., Шаевич Я.Е. Опорные инженерногеологические разрезы лессовых пород Северной Евразии. Монография. Москва: КДУ; 2008. 608 с.
2. Xiaoyu Zhu, Jessica Gray, Ying Gu, Tong He. Genesis of Loess Particles on the Chinese Loess Plateau. Geochemistry, Geophysics, Geosystems. 2022;23(7):e2022GC010428. https://doi.org/10.1029/2022GC010428
3. Торгоев И.А., Алёшин Ю.Г. Оползни сейсмогенного разжижения в лёссовидных суглинках. В: Материалы годичной сессии Научного совета РАН по проблемам геоэкологии, инженерной геологии и гидрогеологии. «Сергеевские чтения. Фундаментальные и прикладные вопросы современного грунтоведения». Москва: ГеоИнфо; 2022. С. 224–229.
4. Королев В.А., Григорьева И.Ю. Эколого-геологические системы массивов лессовых грунтов. Инженерная геология. 2022;ХVII(2):42–64. https://doi.org/10.25296/1993-5056-2022-17-2-42-64.
5. Jianhua Ma, Runqiang Zeng, Xingmin Meng, Zonglin Zhang, Shufen Zhao, Ziran Wei. Field Research on Preferential Infiltration in Rainfall-Induced Loess Landslides. Engineering Geology. 2025;354:108184. https://doi.org/10.1016/j.enggeo.2025.108184
6. Jinduo Yang, Xi-An Li, Lincui Li, Zhang Jing, Weiping Wang. Formation Mechanism of Metastable Internal Support Microstructure in Malan Loess and Its Implications for Collapsibility. Engineering Geology. 2025;346:107892. https://doi.org/10.1016/j.enggeo.2024.107892
7. Shijie Zhai, Guangyin Du, Zhongxun Zhuang, Changhui Gao, Chuanle Wang. Effect of Resonance Compaction Method on the Bearing Capacity Considering Geotechnical Spatial Variability Characteristics. Engineering Geology. 2023;324:107256. https://doi.org/10.1016/j.enggeo.2023.107256
8. Галай Б.Ф. Уплотнение просадочных грунтов глубинными взрывами. Ставрополь: Сервисшкола, 2015. 240 с.
9. Zekun Li, Penghui Ma, Jianqi Zhuang, Qingyi Mu, Jiaxu Kong, Luqing Zhao, et al. Permeability Characteristics, Structural Failure Characteristics, and Triggering Process of Loess Landslides in Two Typical Strata Structures. Engineering Geology. 2024;341:107728. https://doi.org/10.1016/j.enggeo.2024.107728
10. Прокопов А.Ю., Сычев И.В., Рязанцева А.В. Определение модуля деформации закрепленного грунтового основания по данным штамповых испытаний и геотехнического мониторинга. Современные тенденции в строительстве, градостроительстве и планировке территорий. 2023;2(3):17–30. https://doi.org/10.23947/2949-1835-2023-2-3-17-30.
11. Jing Yang, Xirong Niu, Qigao Guo, Zhiheng Wen, Hailong Cao. Strength and Deformation Characteristics of Compacted Loess with Different Moisture Content and Compaction Energy. Results in Engineering. 2023;20:101637. https://doi.org/10.1016/j.rineng.2023.101637
12. Xiaowei Liu, Xudong Zhang, Xiaogang Fu, Tianxiang Yang, Zisong Su. Experimental Study on Creep Characteristics of Saturated Q2 Loess. Frontiers in Earth Science. 2022;10:815275. https://doi.org/10.3389/feart.2022.815275
13. Осипов В.И., Соколов В.Н., Карпенко Ф.С. Физико-химическая механика дисперсных пористых материалов — новый подход к оценке механической устойчивости глинистых грунтов. Геоэкология. Инженерная геология. Гидрогеология. Геокриология. 2024;4:50–63. https://doi.org/10.31857/S0869780924040059.
14. Карпенко Ф.С. Свойства глинистых грунтов с позиций физико-химической теории прочности. Грунтоведение. 2023;2:3–12. https://doi.org/10.53278/2306-9139-2023-2-21-3-12.
15. Петраков А.А., Прокопов А.Ю., Петракова Н.А., Панасюк М.Д. Интерпретация прочностных характеристик грунта для численных исследований. Известия Тульского государственного университета. Науки о Земле. 2021;(1):225–236.
16. Tarasenko ЕО. Mathematical Modeling of the Strength Properties of Lesses by the Method of Correlation-Regression Analysis. International Journal for Computational Civil and Structural Engineering. 2024;20(1):171–181. https://doi.org/10.22337/2587-9618-2024-20-1-171-181
17. Tarasenko EO. Estimation of the Vertical Diffusion Coefficient of Gas in Compacted Soils by Means of Mathematical Modeling. Proceedings of ISP RAS. 2024;36(5):181–190. https://doi.org/10.15514/ISPRAS-2024-36(5)-13
18. Кожевникова П.В., Кунцев В.Е., Дорогобед А.Н., Мотрюк Е.Н. Математическое моделирование распределения достоверности петрофизических параметров при построении геологической модели. Современные наукоемкие технологии. 2021;(2):31–37. https://doi.org/10.17513/snt.38490
19. Jingping Wang, Haichun Ma, Jiazhong Qian, Peichao Feng, Xiaohui Tan, Lei Ma. Experimental and Theoretical Study on the Seepage Mechanism Characteristics Coupling with Confining Pressure. Engineering Geology. 2021;291:106224. https://doi.org/10.1016/j.enggeo.2021.106224
20. Галай О.Б. Буденновск: геология и город. Монография. Ставрополь: Ставропольсервисшкола, 2022. 318 с.
Об авторе
Е. О. ТарасенкоРоссия
Елена Олеговна Тарасенко, кандидат физико-математических наук, доцент, доцент кафедры «Вычислительная математика и кибернетика»
355000, г. Ставрополь, ул. Пушкина, 1
ResearcherIDAAB-2396-2021
ScopusID 57194241084
Разработана математическая модель для оценки мощности заряда при уплотнении лёссов глубинными взрывами. Модель учитывает физико-механические свойства грунтов и их изотропность или анизотропность. Получены аналитические формулы для случаев с выбросом грунта и без выброса. Проведен численный эксперимент, подтвердивший согласие расчетов с натурными данными. Модель позволяет исключить пробные взрывы и сократить затраты при проектировании уплотнения. Метод применим в проектных и изыскательских организациях при планировании инженерно-технологического процесса.
Рецензия
Для цитирования:
Тарасенко Е.О. Математическое моделирование оценки мощности заряда при исключении просадочности лёссов глубинными гидровзрывами. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):233-241. https://doi.org/10.23947/2687-1653-2025-25-3-233-241. EDN: OVUJUV
For citation:
Tarasenko E.O. Mathematical Modeling of Charge Power Assessment with Exclusion of Loess Subsidence by Deep Hydraulic Blasts. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):233-241. https://doi.org/10.23947/2687-1653-2025-25-3-233-241. EDN: OVUJUV
JATS XML














































