Перейти к:
Получение набора вибрационных сигналов подшипника качения с разной степенью развития локального дефекта наружного кольца
https://doi.org/10.23947/2687-1653-2025-25-3-242-255
EDN: CRISFJ
Аннотация
Введение. Создание достоверных тестовых наборов вибрационных сигналов остаётся актуальной задачей вибродиагностики, поскольку отсутствие данных по ранним стадиям дефектов подшипников затрудняет разработку и верификацию алгоритмов диагностики. Экспериментальное получение таких сигналов ограничено отсутствием соответствующих образцов и длительностью процесса накопления повреждений. Существующие подходы на основе численного моделирования требуют высоких вычислительных ресурсов и сложной настройки, что снижает их практическую применимость. Пробелом в исследованиях является отсутствие простой, воспроизводимой и валидированной методики генерации сигналов, отражающих последовательное развитие дефекта. Целью данного исследования является создание упрощённой методики формирования тестового набора сигналов вибрации подшипника, который может использоваться для разработки и верификации новых методов вибродиагностики. Методика основана на комбинировании экспериментальных и смоделированных сигналов.
Материалы и методы. В исследовании использовались экспериментальные данные, полученные с лабораторной установки, моделирующей роторный узел с подшипником качения (тип 180603). Для имитации ранних стадий дефекта (единичная и двойная ямка выкрашивания) применялось динамическое моделирование методом конечных элементов в среде ANSYS Mechanical (версия 16.2) на основе плоских элементов Plane162 с применением пакета LS-DYNA. Полученные последовательности импульсов накладывались на измеренный сигнал исправного подшипника для формирования комбинированных сигналов. Все сигналы (3 экспериментальных, 2 комбинированных) подвергались анализу с использованием преобразования Фурье, полосовой фильтрации (октавная полоса частот 5,4 кГц) и расчёта статистических параметров: СКЗ, пик-фактора и коэффициента эксцесса. Анализ проводился в среде Mathcad (версия 15.0).
Результаты исследования. В результате исследования разработана методика формирования тестового набора вибрационных сигналов подшипника качения, охватывающая исправное состояние и последовательное развитие локального дефекта наружного кольца. Результаты показали корреляцию между амплитудой вибрационных сигналов и стадиями дефектов — наблюдался рост амплитуд в высокочастотной области, что подтверждает взаимодействие тел качения с дефектными поверхностями. Дополнительный статистический анализ выявил увеличение диагностических параметров (среднего квадратического значения, пик-фактора и коэффициента эксцесса) по мере развития повреждения. Установлено, что смоделированные сигналы воспроизводят характерные признаки дефекта и корректно вписываются в общую тенденцию изменения параметров.
Обсуждение. Полученные данные демонстрируют, что предложенная методика позволяет упрощенно формировать эталонные сигналы без необходимости длительного накопления экспериментальных данных или повреждения оборудования. Физическая обоснованность смоделированных импульсов и согласованность динамики роста диагностических параметров с реальными данными подтверждают возможность использования данной методики для стандартизированного тестирования методов вибродиагностики.
Заключение. Разработанная методика обеспечивает эффективное и воспроизводимое формирование тестовых наборов сигналов для вибродиагностики. Она может быть использована для ускоренной верификации алгоритмов, снижения затрат на эксперименты и повышения надёжности диагностики. В дальнейшем планируется упрощение генерации импульсов на основе аналитического моделирования и расширение методики на другие типы подшипников и дефектов.
Для цитирования:
Колосова З.А., Колосова О.П., Шнайдер Д.А. Получение набора вибрационных сигналов подшипника качения с разной степенью развития локального дефекта наружного кольца. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):242-255. https://doi.org/10.23947/2687-1653-2025-25-3-242-255. EDN: CRISFJ
For citation:
Kolosova Z.A., Kolosova O.P., Shnayder D.A. Obtaining a Set of Vibrational Signals from Rolling Bearings with Varying Degrees of Local Defect Development in the Outer Ring. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):242-255. https://doi.org/10.23947/2687-1653-2025-25-3-242-255. EDN: CRISFJ
Введение. В современной промышленности наблюдается тенденция к увеличению размеров, сложности и производительности машинного оборудования, вследствие чего возрастают капитальные затраты на его приобретение, ремонт и техническое обслуживание. Остановки оборудования приводят к значительным убыткам из‑за недополученной продукции.
Значительная часть ротационного промышленного оборудования содержит подшипники качения. В большинстве случаев именно их техническое состояние является решающим фактором обеспечения безаварийной эксплуатации — то есть отказ подшипника качения ведёт к отказу всего изделия. Специалисты по вибродиагностике сталкиваются с необходимостью анализа и интерпретации вибрационных сигналов для оценки состояния подшипников качения. Наличие набора сигналов, отражающих различные стадии развития дефектов, является критически важным для разработки и тестирования новых методов диагностики. Это позволяет не только повысить точность и надёжность диагностических алгоритмов, но и обеспечить их адаптацию к реальным условиям эксплуатации оборудования. Однако получение такого набора сигналов в реальных условиях представляет собой непростую задачу [1]. Традиционные методы включают либо ожидание естественного появления дефекта, что может занять значительное время, либо намеренное повреждение подшипника, что не всегда целесообразно и может привести к дополнительным затратам. В связи с этим возникает необходимость разработки альтернативных подходов к получению вибрационных сигналов с разной степенью развития дефекта.
Одним из таких способов является математическое моделирование и симуляция вибрационных сигналов подшипников [2]. Исследователи разработали различные модели, включая системы с тремя [3] и двумя степенями свободы [4]. Эти модели учитывают такие факторы, как радиальный зазор, количество шариков и локализованные дефекты на внутреннем кольце, внешнем кольце или шариках. Были предложены усовершенствованные стохастические модели, учитывающие случайное скольжение роликовых элементов и периодически изменяющиеся передаточные функции [5]. Симуляции с использованием MATLAB применялись для генерации временных сигналов вибрации и частотных спектров [4].
Тем не менее моделирование сигналов вибрации подшипников остаётся нетривиальной задачей, связанной с рядом технических и методологических трудностей. Во‑первых, реальные системы подшипников обладают высокой степенью сложности [6]. Точное представление в одной модели всех факторов, влияющих на вибрации подшипников, практически невозможно. Модели часто упрощают сложные взаимодействия между компонентами, что может приводить к потенциальным неточностям в предсказаниях. Во‑вторых, подшипники демонстрируют нелинейное динамическое поведение, особенно при наличии дефектов [7]. Эта нелинейность трудно улавливается в математических моделях, особенно когда речь идёт о составных дефектах — таких, как одновременные дефекты на внутреннем и внешнем кольцах. В‑третьих, проблема заключается в неопределённости параметров [8]. Многие модели зависят от параметров, которые трудно измерить или точно оценить, таких как жёсткость контакта и коэффициенты демпфирования. Это добавляет дополнительную сложность в процесс моделирования и может привести к неточностям в результатах [9]. Более комплексные модели требуют значительных вычислительных ресурсов, что делает анализ в реальном времени сложным для промышленных приложений. Некоторые модели могут игнорировать важные факторы, такие как температурные эффекты, условия смазки или вариации в производстве, что приводит к расхождениям между предсказанным и фактическим поведением [9]. Вследствие нехватки калибровочных подшипников возможности экспериментальной валидации ограничены, что ставит под вопрос полноту и надёжность верификации разработанных математических моделей [10].
Целью настоящего исследования является разработка упрощённой методики формирования тестового набора вибрационных сигналов подшипников, отражающих различные типы и стадии дефектов, и проверка её применимости для тестирования и верификации алгоритмов вибродиагностики. Предложенный подход направлен на преодоление ограничений существующих методов моделирования, связанных с высокой вычислительной сложностью и недостаточной адекватностью воспроизведения реальных условий работы системы.
Для достижения поставленной цели была разработана методика, сочетающая экспериментальное снятие исходного сигнала с оборудования в исправном состоянии с конечно‑элементным моделированием поведения системы при наличии дефектов. На основе моделирования была получена последовательность импульсов, имитирующих влияние повреждения подшипника. Эти импульсы добавлялись к исходному сигналу, создавая набор комбинированных сигналов, соответствующих различным стадиям развития дефекта.
Такой подход позволяет сформировать стандартизованный и легко воспроизводимый набор данных, который может быть использован для тестирования и сравнительной оценки различных методов вибродиагностики. Предложенная методика симуляции дефектных сигналов представляет собой перспективное направление для развития вибродиагностики и может быть полезна для различных отраслей промышленности, где важна надёжность и долговечность оборудования.
Материалы и методы. Разработка методики получения набора сигналов подшипника с различными стадиями развития дефекта включает следующие этапы: получение исправного сигнала экспериментальным путём, создание модели исследуемого подшипника, имитация дефекта на модели, получение последовательности импульсов дефекта и подмешивание этой последовательности к реальному исправному сигналу.
Получение исправного сигнала с лабораторной установки целесообразно, поскольку при моделировании трудно учесть множество факторов, влияющих на реальный сигнал — такие как шум от самого оборудования, шум от прибора измерения, присутствующий дисбаланс валов оборудования и т.д.
Для сравнения реальных и смоделированных сигналов на лабораторной установке также были получены сигналы подшипников с дефектами. Для получения последовательности импульсов применялось моделирование методом конечных элементов (МКЭ), который является одним из наиболее эффективных и широко используемых подходов к численному анализу механических систем и структур [10]. Полученные с помощью МКЭ последовательности импульсов были сложены с реальным исправным сигналом для формирования сигналов с дефектом.
1. Получение исправного сигнала экспериментальным путем
В качестве объекта исследования выбран шариковый радиальный однорядный подшипник с уплотнением типа 180603 ГОСТ 8 882–751. Геометрические характеристики данного подшипника приведены в таблице 1.
Таблица 1
Геометрические характеристики подшипника качения
|
Характеристика, размерность |
Обозначение, формула |
Значение |
|
Габаритные размеры |
||
|
Внешний диаметр, мм |
D |
47 |
|
Внутренний диаметр, мм |
d |
17 |
|
Ширина, мм |
B |
19 |
|
Размеры тел качения |
||
|
Диаметр, мм |
db |
9,5 |
|
Количество |
z |
6 |
|
Угол контакта, рад |
β |
0 |
|
Угловой шаг тел качения, рад |
g = 2π/z |
π/3 |
|
Диаметр окружности, проходящей через центры тел качения, мм |
D0 = (D+d)/2 |
32 |
|
Начальный радиальный зазор, мкм |
g |
8–15 |
|
Размеры дорожек качения |
||
|
Наименьшая толщина по желобу, мм |
h = [(D–d)/2–db]/2 |
2,75 |
|
Диаметр внешней дорожки, мм |
do = D–2×h |
41,5 |
|
Диаметр внутренней дорожки, мм |
di = d+2×h |
22,5 |
|
Радиус поперечного профиля, мм |
r = 0,515×db |
4,893 |
Схема подшипника приведена на рис. 1.

Рис. 1. Схема подшипника качения
Подшипники данного типа установлены в опоры лабораторной установки, которая моделирует простейшую ротационную машину и принципиально представляет собой ротор на двух опорах. Как и в любой реальной машине, в схеме установки присутствуют такие дефекты изготовления, как статический и динамический дисбаланс, перекос и излом осей, что приближает условия работы подшипника установки к реальным.
Конструктивно лабораторная установка, схема которой показана на рис. 2, состоит из платформы-основания, на которой крепятся две опоры и асинхронный электродвигатель типа 4А80А мощностью 1,1 кВт с номинальной частотой вращения 1000 об/мин. В опорах на подшипниках качения вращается вал с маховиком. Вал соединён с двигателем с помощью муфты.
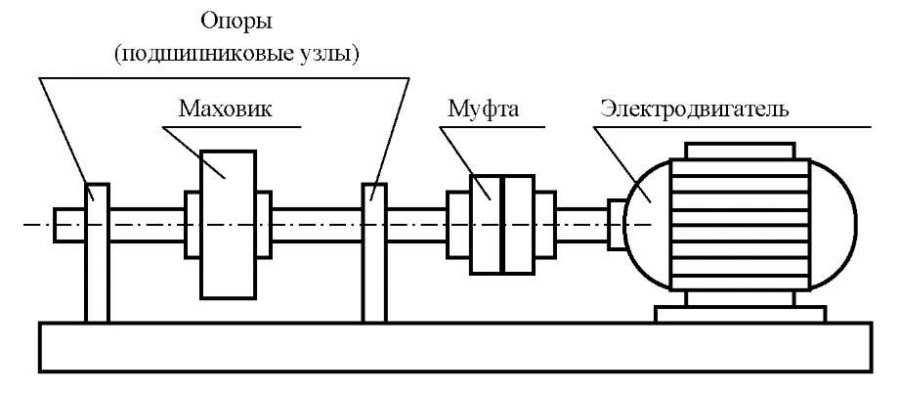
Рис. 2. Схема лабораторной установки
Из-за наличия трения в подшипниках частота вращения ротора лабораторной установки несколько отличается от номинальной частоты вращения двигателя и составляет 995 об/мин, или 16,58 Гц, или 104,2 рад/с. В правую опору установки (ближнюю к двигателю и менее доступную) помещается новый исправный подшипник. Изучаемый подшипник находится в удаленной от двигателя левой опоре в радиальном вертикальном направлении.
Для экспериментального изучения вибраций подшипника качения была использована измерительная система, показанная на рис. 3. Измерительная система включает в себя пьезоэлектрический акселерометр, усилитель сигнала, осциллограф, аналого‑цифровой преобразователь (АЦП) и ЭВМ. Кроме этого, для калибровки измерительной системы вместо акселерометра и усилителя подключался генератор сигналов.
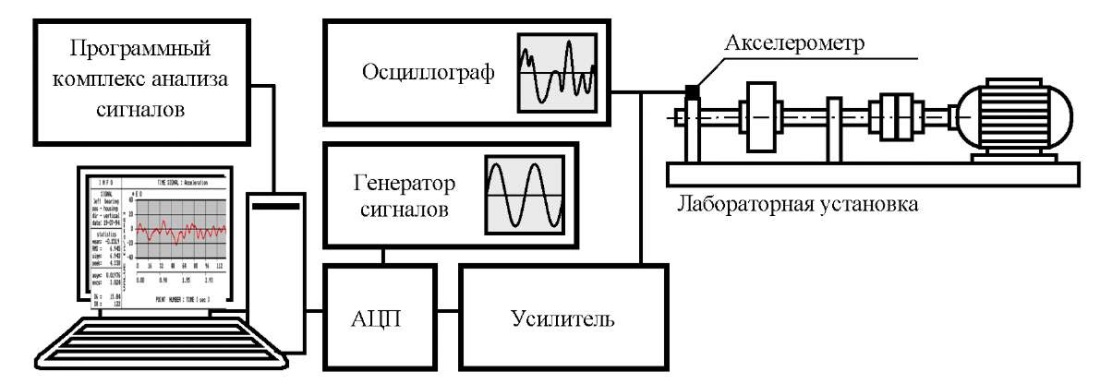
Рис. 3. Измерительная система
В левую опору лабораторной установки последовательно устанавливались три подшипника типа 180603 по ГОСТ 8882–752:
- исправный подшипник качения;
- неисправный подшипник с развитым дефектом (интенсивное выкрашивание дорожек качения);
- подшипник в аварийном состоянии с трещиной наружного кольца.
С каждого из перечисленных подшипников были сняты сигналы виброускорения с частотой дискретизации 16 кГц и длительностью 0,12 секунд.
2. Построение модели подшипника с применением метода конечных элементов
Модель исправного подшипника качения, помещённого в опору лабораторной установки, изображена на рис. 4. Модель построена с использованием элементов Plane162. Упругая опора лабораторной установки жёстко закреплена по основанию. В опору вставлен подшипник — при этом опора и внешнее кольцо подшипника по линии касания имеют общие узлы. Вал и внутреннее кольцо подшипника соединены аналогично. Внешнее и внутреннее кольца подшипника упругие. Вал и сепаратор — жёсткие. Тела качения моделируются следующим образом: центральная часть шарика жёсткая, периферия упругая.
Во всех упругих элементах модели используется материал со свойствами: Е = 210 ГПа; μ = 0,33; ρ = 7 850 кг/м³. В материал введено демпфирование Рэлея.
Нагрузки на модель:
- валу, как жёсткому телу, задан закон движения — угол поворота вокруг оси z от времени φ(t) = ωt;
- к валу приложена радиальная нагрузка q1= q0, направленная вертикально вниз (моделируется статическая нагрузка подшипника);
- к валу приложена радиальная нагрузка q2= q0/2, направление которой поворачивается вместе с валом вокруг оси z (моделируется дисбаланс).

Рис. 4. Модель подшипника на основе элементов Plane162
Для облегчения задачи в вычислительном смысле были введены следующие упрощения модели.
- Введены полые шарики, что привело к снижению числа узлов в модели. При этом плотность жесткой части шарика пересчитывается так, что масса шарика остаётся неизменной.
- Вблизи контактных поверхностей сетка конечных элементов уплотнена. Размеры элементов в этих зонах минимальны.
- Структурные элементы системы, жёсткостью которых можно пренебречь (вал, сепаратор), выполнены из материала «Rigid».
Особенность расчёта рассматриваемой модели заключается в том, что для последующей обработки вычисленного сигнала виброускорения (в частности, для применения к нему быстрого преобразования Фурье) необходимо, чтобы шаг записи сигнала по времени был постоянным.
3. Моделирование локального дефекта наружного кольца подшипника
Задачей расчётно‑экспериментального исследования является получение вибросигналов подшипника для разных степеней развития локального дефекта наружного кольца подшипника качения. Задача решается путём наложения на измеренный сигнал исправного подшипника последовательности кратковременных быстрозатухающих «единичных импульсов», вызванных попаданием тела качения на дефект (ямку выкрашивания). Последовательность импульсов получим с помощью модели МКЭ.
Глубину ямки выкрашивания будем считать равной глубине залегания опасной точки в зоне контакта тела качения и дорожки при нарушении условия выносливости — достижении равенства амплитудного значения максимального эквивалентного напряжения в контакте тела и дорожки качения пределу выносливости материала — стали ШХ15:
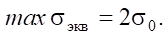 (1)
(1)
Предел выносливости стали ШХ15 ГОСТ 801–793 при термообработке по типу «закалка при 840 °С в масле и отпуск при 300 °С», применяемой для шарикоподшипников, равен σ₋₁ = 650 МПа. Однако предел выносливости σ₋₁ для симметричного цикла напряжений не подходит для расчётов на контактную прочность, поскольку цикл контактных напряжений является отнулевым (пульсационным). Предел выносливости в отнулевом цикле σ₀ определяется с использованием схематизированной диаграммы предельных амплитуд, связывающей среднее напряжение цикла σₘ и его амплитудное напряжение σa = σ–1 – ψσₘ, где коэффициент ψ = 0,2–0,3 для легированных сталей. Откуда:
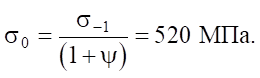 (2)
(2)
Для определения максимального эквивалентного напряжения рассмотрим напряжённое состояние в точке, расположенной на глубине z под центром эллиптической площадки контакта. Введём систему координат Cxyz: C — центр эллиптической площадки контакта, ось z перпендикулярна площадке контакта, ось x направлена по большой полуоси площадки контакта, ось y — по малой полуоси площадки контакта. Полуоси площадки контакта: большая — a, малая — b. Для удобства записи формул обозначим: a/b = β, z/a = ζ.
В площадках, параллельных координатным плоскостям, касательные напряжения равны 0, нормальные напряжения являются главными и определяются по следующим формулам:
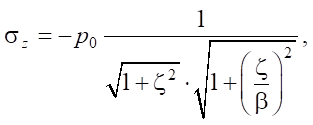 (3)
(3)
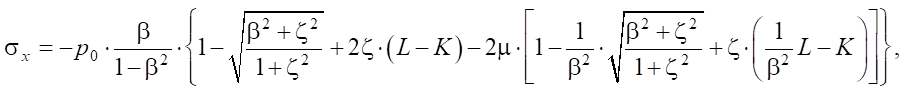 (4)
(4)
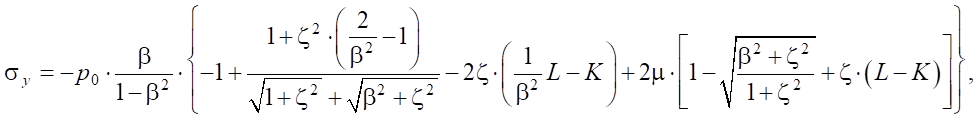 (5)
(5)
где K(e), L(e) — полные эллиптические интегралы, зависящие от эксцентриситета e эллиптической площадки контакта тела качения и кольца подшипника.
Эксцентриситет площадки контакта e, наибольшая интенсивность давления между соприкасающимися телами p0, малая полуось эллиптической площадки контакта находятся из задачи Герца контакта шарообразных тел качения и тороидальной дорожки качения.
Эквивалентное растягивающее напряжение определяется из (3), (4) и (5) по гипотезе прочности Губера-Мизеса:
 (6)
(6)
По результатам проведённого расчёта с использованием формул (1), (2) и (6) для рассматриваемого подшипника глубина ямки выкрашивания на внутренней дорожке составила 0,56 мм, на наружной дорожке — 0,60 мм. Предполагая форму ямки выкрашивания полусферической, ее поперечный размер (диаметр) будем считать равным удвоенной глубине.
В плоской модели исправного подшипника качения на наружной дорожке качения введем дефект в виде v-образной выемки (рис. 5). Ширину и глубину дефекта округлим и примем равными 0,5 мм.

Рис. 5. Модель дефекта наружного кольца подшипника
Такое изменение в модели исправного подшипника может описывать единичную ямку выкрашивания. Причём для единичной ямки выкрашивания получить экспериментальный вибросигнал практически невозможно из‑за большой длительности и трудоёмкости эксперимента. Рассмотрен также локальный дефект удвоенной ширины, соответствующий «двойной» ямке выкрашивания — двум близко расположенным ямкам, слившимся в одну. С использованием данных моделей в программе LS‑DYNA были рассчитаны сигналы виброускорения в вертикальном направлении верхней точки опоры, лежащей на оси симметрии.
Расчет проводился для следующих параметров:
- размеры конечных элементов в зонах контакта aэл ≈ 0,8мм;
- величина демпфирования в материале b =0,25;
- параметр радиальной нагрузки q0 = 2160кН/м;
- время реализации процесса Т = 1,2с;
- шаг записи сигнала по времени Δt = 1мкс.
4. Обработка набора сигналов
В результате описанных выше методов измерения и симуляции был сформирован набор вибросигналов, включающий три сигнала, измеренных на лабораторной установке, и два сигнала, полученных путём смешения смоделированных импульсов дефекта с реальным сигналом исправного подшипника. Комбинированные сигналы предназначены для заполнения пробелов в выборке и компенсации отсутствия экспериментальных данных по подшипникам с дефектом на ранней стадии.
Для анализа временных и частотных характеристик вибросигналов применялось быстрое преобразование Фурье, позволившее получить амплитудные спектры в частотной области. Анализ спектров проводился в широком частотном диапазоне (0–8 кГц).
Для выделения импульсов, вызванных локальными дефектами, сигналы фильтровались в октавной полосе частот 5,4 кГц. Полученные узкополосные сигналы использовались для идентификации импульсов дефекта и расчёта их максимальных амплитуд.
Среднее значение максимальных амплитуд импульсов рассчитывалось как среднее арифметическое по всем выделенным импульсам в узкополосном сигнале. Этот параметр использовался для количественной оценки выраженности дефекта.
Для количественной оценки и сравнения сигналов были рассчитаны следующие статистические параметры: среднеквадратичное значение (СКЗ) виброускорения, пик-фактор и коэффициент эксцесса. Выбор этих параметров обоснован их эффективностью в выявлении локальных дефектов подшипников [11][12].
СКЗ рассчитывалось по следующей формуле [13]:
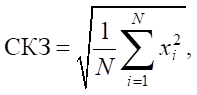 (7)
(7)
где x i — i-тое значение виброускорения, N — число отсчетов сигнала.
Пик-фактор определялся как отношение пикового значения сигнала к СКЗ [14]:
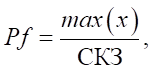 (8)
(8)
где x — значения виброускорения.
Коэффициент эксцесса рассчитывался по формуле для большой выборки (N > 100) [15][16]:
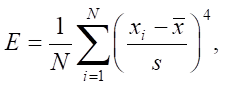 (9)
(9)
где 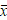 обозначает среднее арифметическое значение виброускорения, s — стандартное отклонение.
обозначает среднее арифметическое значение виброускорения, s — стандартное отклонение.
Рассчитанные параметры были использованы для построения таблицы соответствия степени развития дефекта наружного кольца подшипника, что позволило оценить правдоподобие смоделированных сигналов и их пригодность для тестирования методов вибродиагностики.
Результаты исследования
1. Измеренные сигналы
Были получены три сигнала, соответствующие различным состояниям подшипника: исправное состояние, развитый дефект (множественные ямки), аварийное состояние (трещина кольца). На рис. 6 представлены формы вибросигналов в временной области (1 — исправный подшипник качения; 2 — неисправный подшипник с развитым выкрашиванием дорожек качения; 3 — подшипник в аварийном состоянии с трещиной наружного кольца).
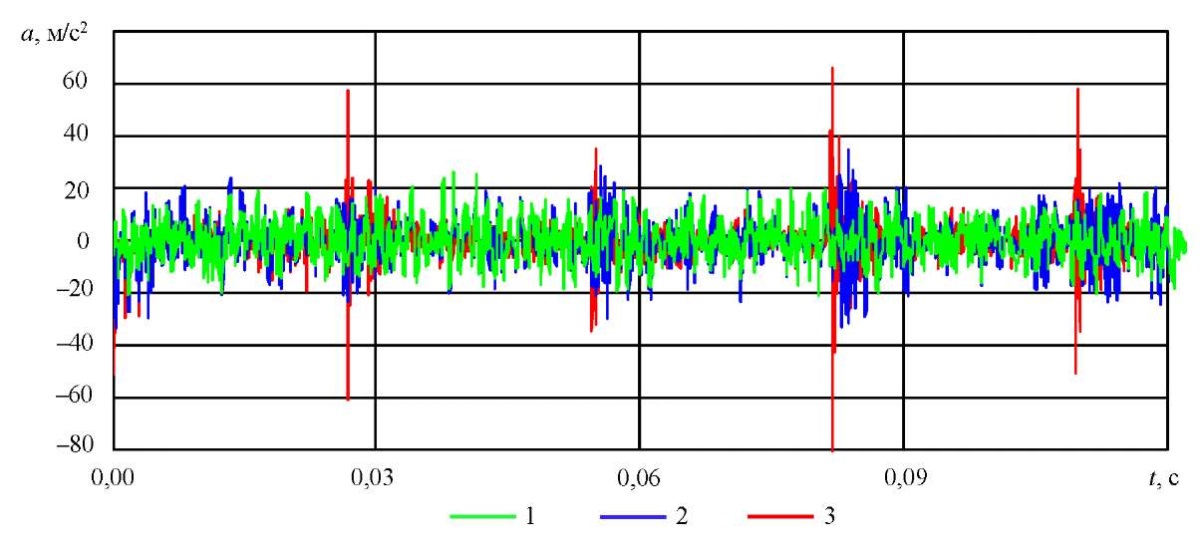
Рис. 6. Измеренные сигналы виброускорения
На рис. 7 показаны амплитудные спектры сигналов в частотной области (1 — исправный подшипник качения; 2 — неисправный подшипник с развитым выкрашиванием дорожек качения; 3 — подшипник в аварийном состоянии с трещиной наружного кольца). При развитии дефекта наблюдается рост амплитуд в высокочастотной области (около 5,4 кГц), а в сигналах появляются последовательности кратковременных импульсов.
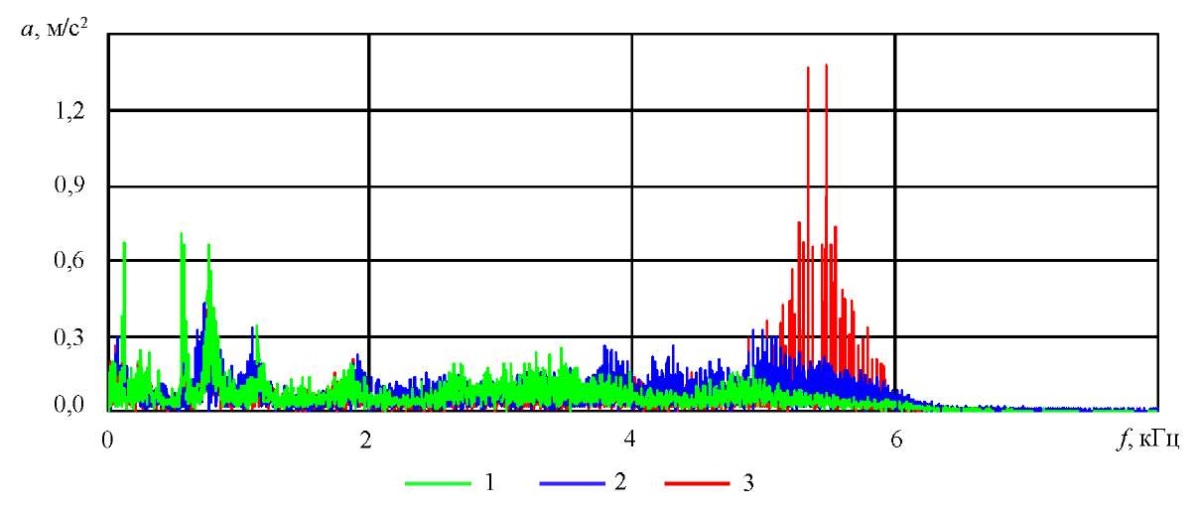
Рис. 7. Амплитудные спектры измеренных вибросигналов
После фильтрации в октавной полосе 5,4 кГц были выделены импульсы дефекта. Узкополосные сигналы представлены на рис. 8 и 9.
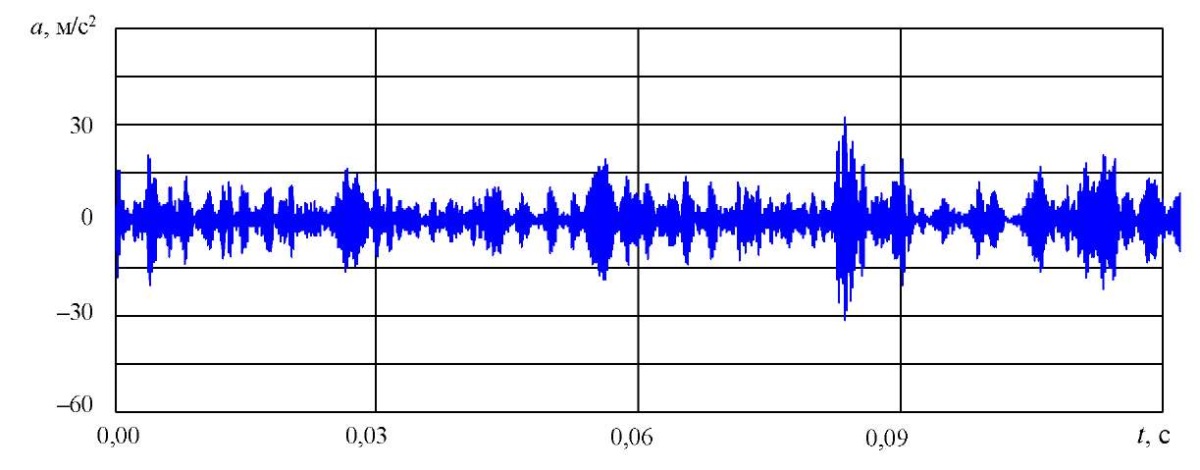
Рис. 8. Узкополосный вибросигнал подшипника качения с развитым выкрашиванием дорожек качения
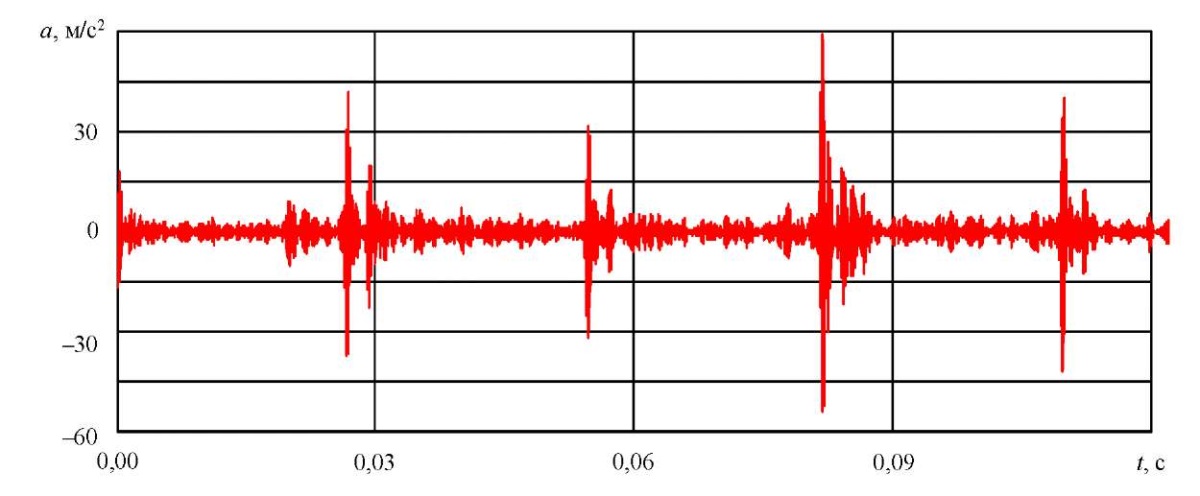
Рис. 9. Узкополосный вибросигнал подшипника качения с трещиной наружного кольца
Среднее значение максимальных амплитуд импульсов составило: 24,3 м/с² — для крупной множественной ямки (последовательность самых сильных импульсов в сигнале подшипника с выкрашиванием); 39,8 м/с² — для трещины кольца.
2. Комбинированные сигналы
Импульсы, полученные динамическим моделированием модели МКЭ, изображены на рис. 10. Исправный сигнал с установки, с которым смешивались полученные импульсы, приведен на рис. 11.
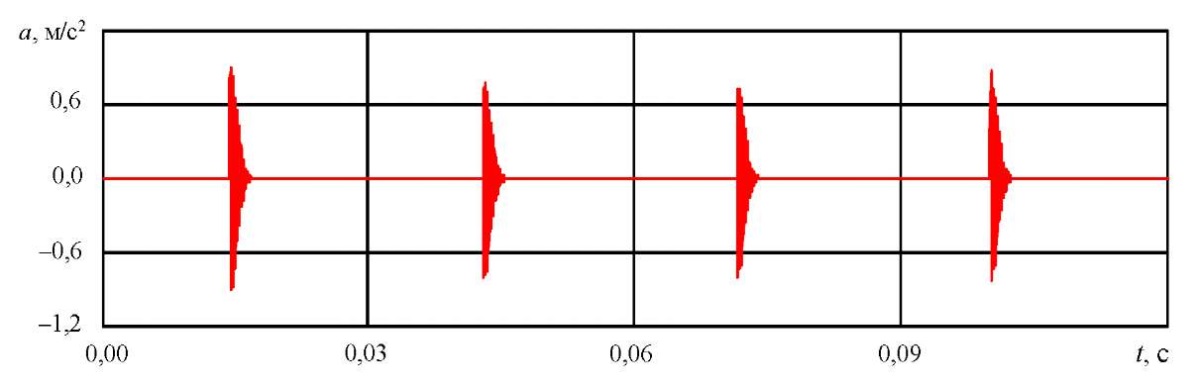
Рис. 10. Последовательность полученных импульсов

Рис. 11. Измеренный вибросигнал исправного подшипника
Были сформированы два комбинированных сигнала, соответствующие ранним стадиям дефекта: с единичной и двойной ямкой выкрашивания. На рис. 12 показаны временные представления полученных сигналов (1 (зелёная линия) — вибросигнал исправного подшипника; 2 (синяя линия) — комбинированный вибросигнал неисправного подшипника с единичной ямкой выкрашивания; 3 (красная линия) — комбинированный вибросигнал неисправного подшипника с двойной ямкой выкрашивания).
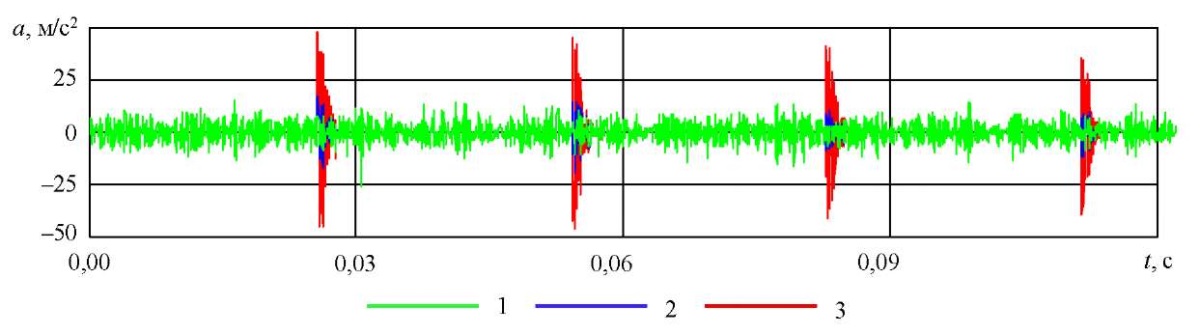
Рис. 12. Комбинированные вибросигналы подшипника качения для разных степеней развития дефекта
Сигнал с единичной ямкой визуально мало отличается от исправного вследствие относительной малости импульсов.
После фильтрации в полосе 5,4 кГц были выделены импульсы дефекта. На рис. 13 представлен узкополосный сигнал для единичной ямки.
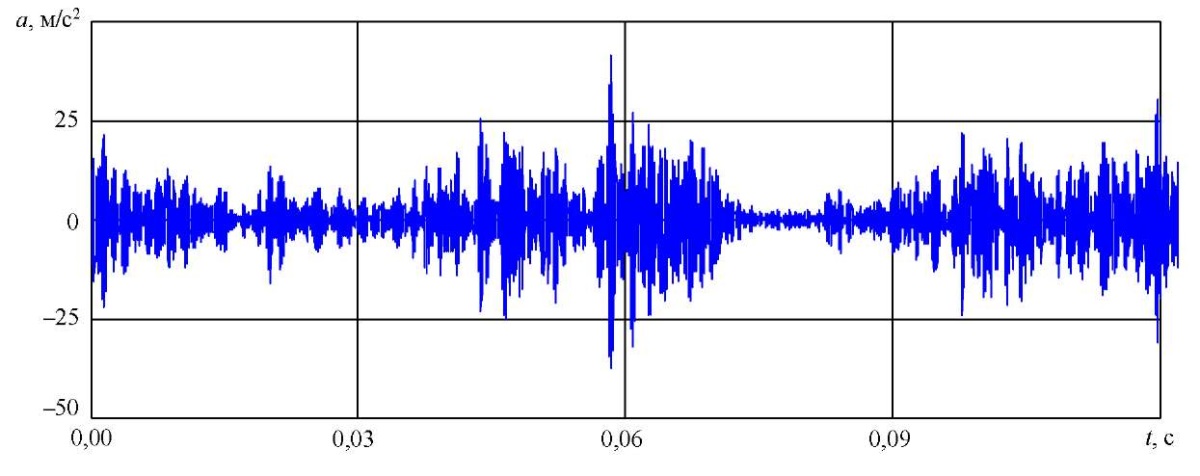
Рис. 13. Узкополосный сигнал подшипника с единичной ямкой выкрашивания
Среднее значение максимальных амплитуд импульсов составило:
- 9,6м/с²— для единичной ямки;
- 14,7м/с²— для двойной ямки.
3. Сравнение статистических параметров измеренных и расчетных сигналов
Для всех сигналов были рассчитаны статистические параметры:
- среднее значение максимальной амплитуды импульсов дефекта А;
- среднее квадратическое значение СКЗ, рассчитанное по формуле (7);
- пик-фактор Pf, рассчитанный по формуле (8);
- коэффициент эксцесса Е, рассчитанный по формуле (9).
Результаты представлены в таблице 2.
Таблица 2
Результаты статистического анализа расчетных вибросигналов для исправного и дефектных подшипников качения
|
Сигнал |
Техническое состояние |
A, м/с² |
СКЗ |
Pf |
E |
|
Измеренный |
Исправное, нет дефекта |
0 |
6,81 |
3,04 |
3,03 |
|
Комбинированный |
Неисправное, ранняя степень развития — единичная ямка |
10 |
6,86 |
3,86 |
3,10 |
|
Комбинированный |
Неисправное, развитый дефект — двойная ямка |
15 |
6,93 |
4,49 |
3,27 |
|
Измеренный |
Неисправное, развитый дефект —множественная ямка |
25 |
7,15 |
5,64 |
4,30 |
|
Измеренный |
Аварийное, трещина кольца |
40 |
7,67 |
6,96 |
8,09 |
На рис. 14 показано изменение нормированных значений статистических параметров в зависимости от степени развития дефекта.

Рис. 14. Рост статистических параметров в зависимости от развития дефекта
Обсуждение. Основной целью данного исследования была разработка методики формирования набора вибросигналов подшипника на различных стадиях развития локального дефекта наружного кольца. Предложенный подход, сочетающий экспериментальные данные и численное моделирование, позволил восполнить пробелы в экспериментальной базе, особенно на ранних стадиях дефекта, получение которых в лабораторных условиях затруднено из‑за отсутствия соответствующих образцов.
Анализ полученных сигналов показал, что по мере развития дефекта наблюдаются характерные изменения как во временной, так и в частотной областях. В сигналах появляются последовательности кратковременных импульсов, а в спектрах — рост амплитуд в окрестности собственной частоты подшипникового узла — ~5,4 кГц. Эти изменения обусловлены ударным характером взаимодействия тел качения с дефектной поверхностью. При попадании дефекта в зону контакта возникает удар, возбуждающий собственные колебания узла. Амплитуда этих колебаний модулируется частотой мелькания дефекта, что проявляется в виде затухающих импульсов в узкополосном сигнале.
Статистический анализ выявил устойчивый рост ключевых диагностических параметров — СКЗ, пик‑фактора и коэффициента эксцесса — по мере увеличения степени повреждения, что согласуется с ожидаемым поведением вибрационного сигнала при развитии локального дефекта. Однако ключевым аспектом анализа была проверка правдоподобия смоделированных сигналов, включённых в набор для компенсации отсутствия экспериментальных данных на ранних стадиях дефекта.
Анализ показал, что значения параметров для комбинированных сигналов логично вписываются в общую тенденцию, наблюдаемую на измеренных сигналах. Так, для сигнала с единичной ямкой (ранняя стадия) СКЗ составило 6,86 м/с², пик‑фактор — 3,86, эксцесс — 3,10; для сигнала с двойной ямкой — 6,93 м/с², 4,49 и 3,27 соответственно. Эти значения находятся между исправным состоянием и развитым дефектом, что указывает на последовательное и физически обоснованное изменение сигнала при увеличении степени повреждения.
Таким образом, смоделированные сигналы не только восполняют пробелы в наборе, но и сохраняют корректную динамику изменения диагностических параметров, что подтверждает их валидность и пригодность для использования в качестве эталонных сигналов при разработке и тестировании методов вибродиагностики. Однако анализ трендовой характеристики показал, что рост параметров не соответствует пороговым значениям, указанным в стандарте ГОСТ Р ИСО 20816–1–20214 (увеличение в 2,5 раза для неисправного состояния и в 10 раз — для аварийного). Это позволяет предположить, что унифицированные пороги могут быть недостаточно точными для конкретных типов оборудования и требуется индивидуальная калибровка диагностических моделей на основе экспериментальных или смоделированных данных. Предложенная методика позволяет проводить такую калибровку без необходимости длительного сбора статистики отказов или намеренного повреждения оборудования.
Важным преимуществом подхода является возможность моделирования развития дефекта для конкретного подшипника и условий эксплуатации. Тем не менее, метод имеет ограничения. В частности, создание конечно‑элементной модели требует значительных временных и квалификационных ресурсов. Для снижения трудоёмкости были проанализированы основные характеристики импульсов, генерируемых дефектом:
- несущая частота импульса равна собственной частоте подшипникового узла — 5,4 кГц;
- наибольшие амплитуды импульсов — случайные со средним значением 1 м/с²;
- частота следования импульсов совпадает с частотой дефекта (мелькания тел качения по наружному кольцу);
- начальная фаза — случайная;
- форма импульса — затухающая по экспоненте.
Распределение амплитуд и характер затухания соответствуют тем, что наблюдаются в реальных сигналах с трещиной кольца. Это указывает на то, что импульс, порождаемый дефектом, поддаётся аналитическому описанию, что позволяет заменить ресурсоёмкое МКЭ-моделирование моделированием заранее заданных форм импульсов и тем самым значительно упростить и ускорить процедуру генерации сигналов.
Таким образом, предложенная методика не только решает задачу формирования полного набора сигналов для вибродиагностики, но и открывает перспективу создания индивидуализированных диагностических моделей, адаптированных под конкретное оборудование. В будущем планируется разработка упрощённого алгоритма генерации импульсов на основе полученных характеристик, что сделает методику более доступной для практического применения.
Заключение. В ходе исследования была разработана методика формирования тестового набора вибросигналов подшипников качения, сочетающая экспериментальные данные и численное моделирование. Предложенный подход позволяет воспроизводить различные стадии развития локального дефекта наружного кольца, включая ранние, для которых отсутствуют экспериментальные образцы, без необходимости длительного накопления данных или повреждения оборудования.
Анализ показал, что смоделированные сигналы корректно вписываются в общую тенденцию изменения диагностических параметров (СКЗ, пик‑фактор, эксцесс), что подтверждает их валидность и пригодность для тестирования методов вибродиагностики. Полученный набор сигналов может служить стандартизированной основой для сравнительной оценки алгоритмов диагностики.
Практическая значимость работы заключается в сокращении затрат на экспериментальные исследования, ускорении верификации диагностических моделей и повышении надёжности оценки технического состояния оборудования.
В дальнейшем планируется упрощение генерации импульсов на основе выявленных математических характеристик, расширение методики на другие типы подшипников и дефектов, а также её интеграция с методами анализа данных для создания решений в области предиктивного обслуживания.
1. ГОСТ 8 882–75 (СТ СЭВ 3 793–82) Подшипники шариковые радиальные однорядные с уплотнениями. Технические условия. Электронный фонд правовых и нормативно-технических документов. URL: https://base.garant.ru/5926172/ (дата обращения: 09.06.2025).
2. ГОСТ 8882–75 (СТ СЭВ 3793–82) Подшипники шариковые радиальные однорядные с уплотнениями. Технические условия. Электронный фонд правовых и нормативно-технических документов. URL: https://base.garant.ru/5926172/ (дата обращения: 09.06.2025).
3. ГОСТ 801–79. Шарикоподшипниковая сталь.
4. ГОСТ Р ИСО 20816–1–2021. Вибрация. Измерения вибрации и оценка вибрационного состояния машин. Электронный фонд правовых и нормативно-технических документов. URL: https://docs.cntd.ru/document/1200182677 (дата обращения: 20.05.2025).
Список литературы
1. Nguyen Duc Thuan, Hoang Si Hong. HUST Bearing: A Practical Dataset for Ball Bearing Fault Diagnosis. arXiv. 2023. https://doi.org/10.48550/arXiv.2302.12533
2. Jing Liu, Yimin Shao. A New Dynamic Model for Vibration Analysis of a Ball Bearing due to a Localized Surface Defect Considering Edge Topographies. Nonlinear Dynamics. 2015;79:1329–1351. https://doi.org/10.1007/s11071-014-1745-y
3. Halmos F, Wartzack S, Bartz M. Investigation of Failure Mechanisms in Oil-Lubricated Rolling Bearings under Small Oscillating Movements: Experimental Results, Analysis and Comparison with Theoretical Models. Lubricants. 2024;12(8):271. https://doi.org/10.3390/lubricants12080271
4. Jain PH, Bhosle SP. Mathematical Modeling, Simulation and Analysis of Non-Linear Vibrations of a Ball Bearing due to Radial Clearance and Number of Balls. Materials Today: Proceedings. 2023;72(3):927–936. https://doi.org/10.1016/j.matpr.2022.09.093
5. Menck O. The Finite Segment Method–A Numerical Rolling Contact Fatigue Life Model for Bearings Subjected to Stochastic Operating Conditions. ASME Journal of Tribology. 2023;145(3):031201. https://doi.org/10.1115/1.4055916
6. Wrzochal M, Adamczak S. The Problems of Mathematical Modelling of Rolling Bearing Vibrations. Bulletin of the Polish Academy of Sciences: Technical Sciences. 2020;68(6):1363–1372. https://doi.org/10.24425/bpasts.2020.135398
7. Lihai Chen, Ao Tan, Lixiu Yang, Xiaoxu Pang, Ming Qiu. Defect Size Evaluation of Cylindrical Roller Bearings with Compound Faults on the Inner and Outer Races. Mathematical Problems in Engineering. 2022;2022(2):1–12. https://doi.org/10.1155/2022/6070822
8. Malanchuk Y, Moshynskyi V, Korniienko V, Malanchuk Z. Modeling the Process of Hydromechanical Amber Extraction. E3S Web of Conferences. 2018;60:00005. https://doi.org/10.1051/e3sconf/20186000005
9. Ali Safian, Hongsheng Zhang, Xihui Liang, Nan Wu. Dynamic Simulation of a Cylindrical Roller Bearing with a Local Defect by Combining Finite Element and Lumped Parameter Models. Measurement Science and Technology. 2021;32(12):125111. https://doi.org/10.1088/1361-6501/ac2317
10. Tianhe Wang, Lei Chen, Hong Lu, Shaojun Wang, Zhangjie Li, Wei Zhang, et al. Finite Element Dynamic Model and Vibration Signal Simulation of Rolling Bearing with Local Faults. In: Proc. 18th International Manufacturing Science and Engineering Conference. New York NY: ASME. 2023;2:105504. https://doi.org/10.1115/MSEC2023-105504
11. Gururaj Upadhyaya, Kumar HS. A Comparative Study of Statistical Features Used in Rolling Element Bearing Health Diagnosis Using Six Sigma Approach. In: Proc. 2nd Indian International Conference on Industrial Engineering and Operations Management. Southfield, MI: IEOM Society International; 2022. https://doi.org/10.46254/IN02.20220244
12. Jain PH, Bhosle SP. Study of Effects of Radial Load on Vibration of Bearing Using Time-Domain Statistical Parameters. IOP Conference Series: Materials Science and Engineering. 2021;1070:012130. https://doi.org/10.1088/1757-899X/1070/1/012130
13. Trufanov NN, Churikov DV, Kravchenko OV. Application of Spectral Analysis Methods for Data Pre-processing of Anomaly Detection Problem of Vibration Diagnostics in Non-destructive Testing. Journal of Physics: Conference Series. 2021;2127:012028. https://doi.org/10.1088/1742-6596/2127/1/012028
14. Garad A, Sutar KB, Shinde VJ, Pawar AC. Analysis of Vibration Signals of Rolling Element Bearing with Localized Defects. International Journal of Current Engineering and Technology. 2017;7:37–42.
15. Tetter V, Tetter A, Denisova I. Researching the Possibility of Determining the Technical Condition of Rolling Bearings by the Kurtosis Factor. In: Proc. International Russian Automation Conference (RusAutoCon). New York City: IEEE; 2023. P. 149–153. https://doi.org/10.1109/RusAutoCon58002.2023.10272799
16. Puzyr V, Mykhalkiv S. Classification of the Technical Condition of Rolling Bearing by the Scalar Indicators and Support Vector Machines. Progresivna tehnìka, tehnologìâ ta ìnženerna osvìta. 2023.
Об авторах
З. А. КолосоваRussian Federation
Зоя Александровна Колосова, аспирант кафедры «Автоматика и управление»
454080, г. Челябинск, пр. Ленина, д. 76
Scopus ID: 59198139900
О. П. Колосова
Russian Federation
Ольга Петровна Колосова, кандидат технических наук, профессор кафедры «Техническая механика»
454080, г. Челябинск, пр. Ленина, д. 76
Д. А. Шнайдер
Russian Federation
Дмитрий Александрович Шнайдер, доктор технических наук, профессор кафедры «Автоматика и управление»
454080, Челябинская область, г. Челябинск, пр. Ленина, д. 76
Scopus Author ID: 57219166252
ResearcherID: R-6261-2016
Разработана комбинированная методика генерации вибросигналов подшипников на основе опыта и конечно элементного моделирования. Модельный подход позволяет формировать последовательности импульсов, соответствующие разным стадиям локального дефекта. Полученные комбинированные сигналы корректно воспроизводят рост статистических диагностических параметров. Методика восполняет дефицит экспериментальных данных на ранних стадиях дефекта без повреждения оборудования. Набор сигналов пригоден для тестирования и валидации алгоритмов вибродиагностики.
Рецензия
Для цитирования:
Колосова З.А., Колосова О.П., Шнайдер Д.А. Получение набора вибрационных сигналов подшипника качения с разной степенью развития локального дефекта наружного кольца. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):242-255. https://doi.org/10.23947/2687-1653-2025-25-3-242-255. EDN: CRISFJ
For citation:
Kolosova Z.A., Kolosova O.P., Shnayder D.A. Obtaining a Set of Vibrational Signals from Rolling Bearings with Varying Degrees of Local Defect Development in the Outer Ring. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):242-255. https://doi.org/10.23947/2687-1653-2025-25-3-242-255. EDN: CRISFJ
JATS XML














































