Scroll to:
Evaluation of crack resistance of welded joints with soft interlayers
https://doi.org/10.23947/2687-1653-2021-21-4-308-318
Abstract
Introduction. Welded joints in large-sized metal structures (e.g., in the structures of ship hulls) subject to low-cycle fatigue are considered. The characteristic appearance of soft interlayers, which are significantly plastically deformed under working loads, was noted. Deformation of the metal structure with damage, especially in the form of cracks, reduces the strength and reliability of structural elements and joints. Pre-deformation negatively affects plasticity; therefore, much depends on the residual plasticity of the cracking material. At the same time, with a decrease in residual plasticity, such an important reliability indicator as the resistance of the material to crack propagation — the fracture toughness – decreases. The paper is devoted to the development of a model that includes analytical dependences for assessing the crack resistance of metal structures and their welded joints with soft interlayers according to the crack resistance limit for all crack sizes.
Materials and Methods. The theory and methods of linear mechanics of materials destruction, structural-mechanical approach are used. The calculation results were analyzed and compared to the experimental data and other analytical solutions. The numerical experiment was performed for the ferrite-perlite steel grades of 10, 50, 22K, St3sp, etc., widely used in industry, as well as for alloy steels hardened to medium and high strength of 30KhGSA, 37KhN3A, etc. Results. Analytical dependences are obtained for calculating the relative crack resistance limit according to three main known mechanical characteristics of the state of the material of the soft interlayer of the welded joint.
Discussion and Conclusions. The results obtained can be used to assess the crack resistance of pre-deformed structural elements and welded joints (including those with soft interlayers) operating under a transverse load. The results of experimental data and analytical calculations are shown in dimensionless form, which enables to obtain invariant results with respect to the fracture toughness limit.
Keywords
For citations:
Molokov K.A., Novikov V.V. Evaluation of crack resistance of welded joints with soft interlayers. Advanced Engineering Research (Rostov-on-Don). 2021;21(4):308-311. https://doi.org/10.23947/2687-1653-2021-21-4-308-318
Introduction. In welded joints subjected to cyclic loads, cracks often occur and develop, which can cause a dangerous condition of structures and their destruction. Examples of the formation of such cracks in the ship hulls are given in [1]. The kinetics of the formation of macrocracks in welds and their development depend on many factors, which requires comprehensive studies on the crack resistance of welded joints and the development of appropriate mathematical models.
The resistance of the metal to crack propagation is significantly affected by the so-called soft interlayers that appear after welding, which are subjected to plastic deformation. Different sections of the welded joint are characterized by a greater or lesser degree of heterogeneity of the mechanical characteristics of the metal [2]. It depends on many initial conditions of the welding procedure. These include the cooling rate of welded joint zones and processing of welded steel, as well as the content of alloying elements, carbon, etc. O. A. Bakshi considered some problematic issues of viscous and brittle destruction of mechanically inhomogeneous welded joints, the influence of defects and microcracks on the processes occurring in the metal structure under loading, etc. The researchers solved a number of particular problems to increase the strength and durability of welded joints with interlayers [3–6].
In the steady-state welding mode, the width of the heat affected zone (HAZ) and mechanical properties of the metal vary slightly along the length of the welded joint. Therefore, it is advisable to consider the heterogeneity of characteristics in different zones in the welded joint under transverse load. For hardened or heat-treated (heatstrengthened) metals, the appearance of quenching structures or weakened zones, respectively, is characteristic. At the same time, depending on the properties of the steel in its initial state and the parameters of the process, soft zones may form. Here, yield strength σтм and tensile strength σвм of the metal are less than in the adjacent (so-called hard) zones σтт and σвт. Thus, the soft zone will be involved in plastic deformation between areas with characteristics σтт > σтм, σвт > σвм earlier than neighboring ones, and the degree of its influence on the strength of the joint will depend on the scheme of the applied load1. Deformation of the soft interlayer reduces the crack propagation resistance — the intensification of brittle fracture is initiated, in which the critical crack length will decrease dramatically [7].
The objective of this study is to develop analytical dependences and a mathematical model for assessing the crack resistance of welded joints with a soft interlayer as a result of its preliminary plastic deformation.
Assume that some limitation of the linear dimensions of the welded sample (except thickness) under transverse load does not noticeably affect the processes and phenomena considered in the metal structure (except for the formation of a soft interlayer) caused by the thermal welding cycle.
Materials and Methods
Calculated prerequisites. Consider the change in the physicomechanical characteristics of the metal of the soft interlayer when the butt joint is pulled across the seam of a sufficiently large range (Fig. 1).
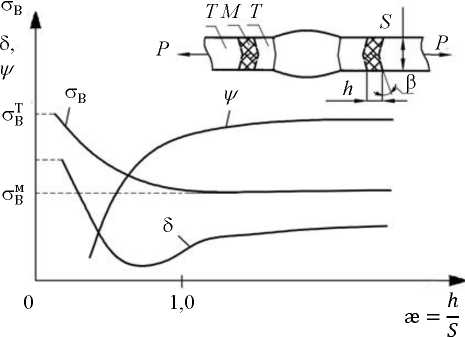
Fig. 1. Diagram of the dependence of characteristics σв , δ and ψ on the relative thickness of the interlayer
In the elastic loading stage, the interlayer and adjacent sections of the considered region are deformed uniformly. When the stress level corresponding to yield strength σтм is reached, a plastic deformation is formed in it, and the adjacent sections remain in an elastic state. To simplify, we assume the angle of inclination of the face of the interlayer β = 0 (Fig. 1). With a further increase in load and deformation, the coefficient of transverse deformation μ (Poisson's ratio) of the soft interlayer increases. As a result, it will be larger than that of the adjacent section of metal. As plastic deformation develops in the interlayer, μ → 0.5, and in the zone with an elastic state of metal, μ = 0.3. Due to unequal transverse deformation, tangential stresses arise in the weld. Their maximum values are concentrated in the area of the separation planes of the soft interlayer and neighboring zones. Tangential stresses prevent transverse narrowing of the soft interlayer in the direction of the sheet thickness. The narrower the interlayer (i.e., the smaller the ratio æ = h⁄s , Fig. 1), the smaller the transverse constriction it receives at the time of the occurrence of true destructive stresses σр. This creates the effect of contact hardening, which provides an increase in load-bearing capacity.
The increase in destructive power has limits. The stronger zones adjacent to the soft interlayer will also be plastically deformed under certain conditions. The greater the strength of the adjacent zones and the smaller the relative thickness of interlayer æ, the more noticeable the effect of contact hardening. It is reinforced by harder interlayers located near relatively soft ones.
Relative transverse constriction ψ in the soft interlayer and the absolute elongation of sample δ depend on æ and the properties of metals in the compound. In wide interlayers, when there is no contact hardening yet, ψ remains constant with decreasing æ (see Fig. 1). And δ gradually decreases with decreasing æ in the total width of the welded sample. In the region of contact hardening, ψ decreases sharply, as transverse tangential stresses increase preventing the narrowing of the interlayers in the direction of the material thickness. In this case, the relative elongation of sample δ also first decreases. When a significant stiffness of the stress state in the soft interlayer is realized, δ increases, since the metal of the hard interlayer is involved in plastic deformation. Note that under welding heat-strengthened steels, δ5м of the soft interlayer turns out to be higher than δ5т. But its plastic deformation is much greater, and the residual plasticity after loading to stresses σвм > σ > σтм may become critical. As a result, the length of the critical crack is significantly reduced, which can occur under the influence of further cyclic operating stresses at the junction of soft and hard interlayers. At the same time, the risk of brittle fracture increases significantly, and its possibility should be assessed (crack resistance limit2 3 [8, 9]) in the area with a crack defect. This takes into account the conditions of plane deformation, contact hardening, and plastically deformed soft interlayer. According to the results of the study of the deformation of interlayers of composite material by the method of finite element modeling [3], it can be noted that the greatest deformation of the soft interlayer is formed near its junction with the hard interlayer. This is especially clear at the average values of the relative thickness of interlayer æ.
Sometimes, with static load, it is possible to find the optimal value of æ and achieve uniform strength of the connection. However, defects or discontinuities existing in the soft interlayer after some deformation may develop into cracks with a critical length, provided that the remaining part of the subcritical deformation is relatively small. The contact hardening degree in the case of plane deformation is determined from the formula2 [2]:
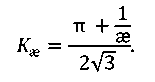 (1)
(1)
Tensile strength of a welded joint with a soft interlayer:
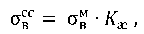 (2)
(2)
where σвм — tensile strength of soft interlayer.
Naturally, to provide equal strength under static load, at least the condition σвсс = σвт is required to be fulfilled. In this case, the limit (minimum) value of the contact hardening coefficient is determined from the ratio of ultimate resistances:
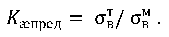 (3)
(3)
Using (1) and (2), we find the limit values of æпред, at which the equal strength of the joint is obtained under the conditions of plane deformation:
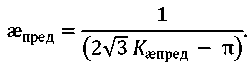 (4)
(4)
However, it must be borne in mind that the increase in the strength of the welded joint with a soft interlayer is limited by the true separation stresses for the soft metal.
When welding hardened steels, the width of the softened zone depends on the rate of energy input and is regulated by the selection of a suitable welding mode. For each metal thickness, welding method, and mode, there is a certain width of the softened section, at which the maximum possible contact hardening is provided, as well as equal strength of the welded joint and the base metal.
The study of the softening section under argon-arc and electron-beam welding of metal with a thickness of 4.5–8 mm shows:
- the hardness on it is determined only by the heating temperature;
- the strength of the joints does not depend on the hardness level of the softened section, but on its width ℎ (Fig. 1).
At the same time, it should be borne in mind that the softening section smoothly passes into harder sections of the heat affected zone.
The study of the kinetics and the mechanism of softening in HAZ allowed us to establish how the properties of the sections surrounding the soft interlayer affect the strength of welded joints.
A new criterion determining the temporary strength limit of the welded joint σврсс is experimentally validated — this is the relative width of the soft interlayer 𝑏1/𝑏0. The proposed empirical dependence has the form:
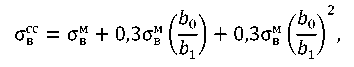 (5)
(5)
where σврсс — the strength limit of the welded joint, MPa; σвм — the strength limit of the soft interlayer, MPa; 𝑏0 — the width of the interlayer with equal strength of the welded joint and the base metal, m; 𝑏1 — the current width of the interlayer, m.
It follows from the last equation that at 𝑏0 = 𝑏1, the soft interlayer is strengthened by a maximum of 60 %, i.e., σвт = 1.6σвм, since further hardening does not make sense.
The experimental results indicate a decrease in the endurance of welded joints with a soft interlayer formed after welding of heat-strengthened steels 𝑈𝑈4 and 𝑈𝑈6. This shows a significant reduction in load-bearing capacity [10]. In these steels, the endurance limits of welded samples without stress concentration almost coincide with the endurance limits of the same samples made of non-hardened steel. That is, despite the thermal hardening of steels (contributing to an increase in strength), the vibration strength of welded joints based on 106 cycles, turns out to be almost the same. Consequently, it can be assumed that plastic deformation in soft interlayers causes early formation of a macrocrack, whose critical size 𝐿с is sharply limited by the plastic deformations that have occurred.
The crack resistance of a plastically deformed soft interlayer material up to the values of σ < σвм can be estimated by a two-parameter fracture criterion — the crack resistance limit, which is calculated according to the known analytical dependence4 [2, 11]:
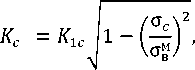 (6)
(6)
where σ𝑐 — gross critical fracture stress; 𝐾1𝑐 — critical stress intensity factor (the constant of the soft interlayer material).
After plastic deformation of the soft interlayer, σc will depend on the characteristics of the defect. Assume that this characteristic is the critical length 𝐿c of the incipient crack. Then, σ𝑐 = 𝐾𝑐⁄√(π𝐿𝑐). However, to use (6), it is necessary to know the degree of deformation of the interlayer, since 𝐾c will primarily depend on it. Value 𝐿c will be considered unknown. It must be determined depending on the deformation of the soft interlayer.
The authors5 [11], investigating the structural parameter of fracture 𝑑𝑑 and determining it for a disc-shaped crack, come to an expression for estimating the crack resistance limit in one-dimensional form:
 (7)
(7)
where η = 𝑎⁄(𝑎 + 𝑑) — dimensionless parameter specified by the range of variation (0 ≤ η ≤ 1); 𝑎 — radius of the disk-shaped crack.
From the last equality, it follows that large cracks are characterized by a relatively small value of 𝑑, а. Destruction occurs with small plastic deformations in the net section, and 𝐾𝑐 ≈ 𝐾1𝑐. The reverse situation develops with relatively small cracks, if a large plastic deformation in the net section is required for destruction, and η ≈ 0, 𝐾𝑐 ≪ 𝐾1𝑐.
Now imagine that the soft interlayer is subjected to cyclic loading. In this case, we use the concept of an effective threshold stress intensity factor 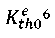 to calculate the limiting amplitude of the loading cycle σ𝑓r at the level of average stresses σвм > σ𝑚 + σ𝑓r > σтм. To this end, we calculate the length of the initial macrocrack 𝐿, corresponding to the limiting amplitude of stresses in a plastically deformed material up to σ𝑚:
to calculate the limiting amplitude of the loading cycle σ𝑓r at the level of average stresses σвм > σ𝑚 + σ𝑓r > σтм. To this end, we calculate the length of the initial macrocrack 𝐿, corresponding to the limiting amplitude of stresses in a plastically deformed material up to σ𝑚:
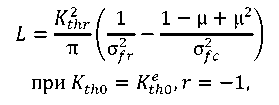 (8)
(8)
where σ𝑓r — limiting stress amplitude; σ𝑓c — cyclic yield strength; 𝑟 — cycle asymmetry coefficient; μ — Poisson's ratio.
The value of the length of the initial macrocrack 𝐿 should be substituted into the calculated dependence for determining the endurance limit [12]:
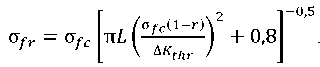 (9)
(9)
The solution will be the desired values of the limiting amplitudes. The characteristics included in (9) are calculated according to [12] or7. Further, it is not difficult to determine the contribution of the preliminary plastic deformation of the soft interlayer to the equivalent damage with regard to estimating the length of the macrocrack.
Research Results
Building a mathematical model. We describe the proposed sequence of analytical dependences development. The remaining plastic properties of the structural element or part of it can be estimated by deformation using the elongation for the material area. We assume that a uniform plastic deformation takes place on a small section of the soft interlayer. It is associated with the critical elongation to destruction δ5(10) through the known dependence [13]:
𝑒 = ln(1 + δ5). (10)
Let us assume that the material of the soft interlayer is plastically deformed. Consider the case when plastic deformation occurs only in the first loading cycles. That is, the area of the soft interlayer is pulled plastically under the external transverse nominal load, and then it works under elastic cyclic stresses. This is how a fatigue crack develops. In a soft interlayer, it can be provoked by high plastic deformation and (or) a defect. Due to the reduction of the ultimate deformation of the soft interlayer material, preliminary plastic deformation causes a decrease in the critical opening at the crack tip. According to the results of work [14], it can be noted that the dependence of the critical crack tip opening δc (CCO) under the pulling deformation of steel is very close to linear. This fact is observed for both aluminum alloy and austenitic steel. The results of the mentioned experiments suggest that with the maximum uniform plastic deformation of these materials, δc = 0.
The endurance limit depends significantly on the degree of pre-deformation. Such a dependence is difficult to obtain theoretically [15], because before the area of the average preliminary plastic deformation of the material, the endurance limit reaches a minimum, and after it increases and can reach the indicators of an undeformed material. Thus, the very fact of the crack appearance, apparently, plays a major role in fatigue. Non-propagating cracks, even with a large preliminary plastic deformation, cause destruction only in rare cases. This is evident from the examples of damage to ship structures given in [1].
We take into account that δc = 0 in the limit of plastic deformation, and use a linear approximation of the dependence δ1c(ε):
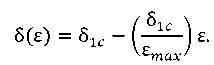 (11)
(11)
At the crack tip, the CCO is determined from the known dependence of linear fracture mechanics:
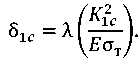 (12)
(12)
Coefficient λ [12] is found from the formula:
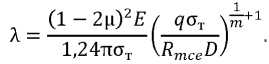 (13)
(13)
Here, 𝐸 — modulus of elasticity of the material; 𝑅𝑚ce — micro-cleavage stress of deformed material; 𝐷 — coefficient taking into account the increase in the first principal stress component for the case of a complex state; 𝑞 — coefficient showing the ratio of the second principal stress component to the first one; 𝑚 — hardening coefficient.
For the specified characteristics and coefficients, there are well-defined design dependences on the basic mechanical characteristics of the material. The critical stress intensity coefficient in (12) is calculated from the formula:
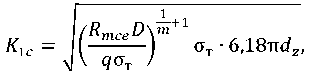 (14)
(14)
where 𝑑𝑧 — average grain diameter of the raw material of the soft interlayer. Substitute the last expression and (13) in (12). Make the necessary reductions. Note that in (12) and (11), a small component of elastic deformations can be neglected. As a result, we get:
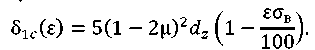 (15)
(15)
Deformation ε is calculated from dependence (10). Let us find dependence 𝐾1𝑐(ε). From (12), we have 𝐾1𝑐(ε) = 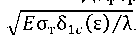 Substitute the known expressions and get:
Substitute the known expressions and get:
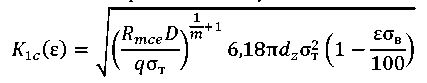 (16)
(16)
or
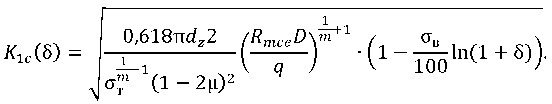 (17)
(17)
After reduction, it is possible to obtain a simple dependence of the critical stress intensity coefficient 𝐾1𝑐 on the current value δ of the soft interlayer pulling:
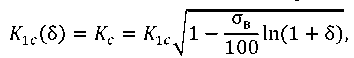 (18)
(18)
where δ — elongation (pulling) of the soft interlayer material, fractions.
In formula (18), 𝐾1𝑐(δ) — crack resistance limit 𝐾𝑐. Its relative value 𝐾1𝑐(δ)⁄𝐾1𝑐 shows how the decrease in the fracture toughness of the material depends on the elongation (pulling) of the elementary region of the soft interlayer. For simplicity of calculations, the averaged elongation of the soft interlayer under the payload can be used. Note that the locality of plastic elongation in the welded joint of a soft interlayer at ∆ℎ relative to ℎ can significantly affect its fatigue strength. For the hardened base material, this effect, on the contrary, will be insignificant
At δ = δ5, ratio 𝐾𝑐⁄𝐾1𝑐 should give zero, so we equate (18) to zero and write down the following calculation formula relative to δ:
δ5 = exp(100⁄σв) − 1. (19)
Here, σв is substituted in MPa.
Analysis of the results and verification of the adequacy of the dependences obtained. It is possible to recognize satisfactory results of verification of the coordination of the design characteristics according to the obtained analytical dependences with reference data of structural hypopearlitic steels in the state of delivery. We are talking about thin-sheet rolled steel St10, St50, 22K, St3sp, 37HN3A, 30HGSA, etc. (Table 1).
Table 1
Design and reference characteristics of steels
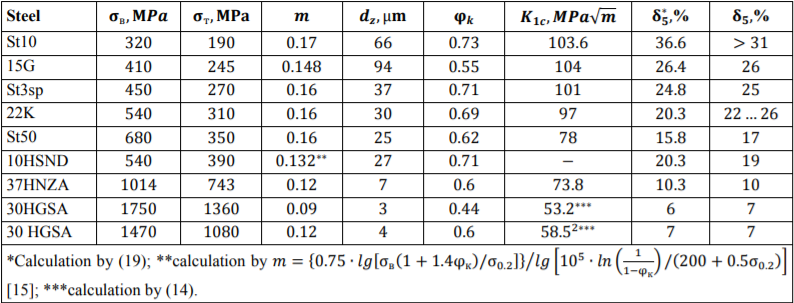
The analysis performed earlier [12] confirms that coefficient λ calculated from (13) at the CCO at the tip 0.618𝑑𝑧, is consistent with the experimental data for steels 22K and St10. In the first case, λ is 0.22, in the second — 0.23.
Let us consider the preliminary deformation of thin sheets in a plane stress with the condition that the grain receives relative elongation 𝑒𝑧 in the longitudinal direction. In this case, its average diameter in the same direction will be larger by (1 + 𝑒𝑧) times, and in the transverse direction, it will decrease by  . That is, if the average diameter increases in the longitudinal direction by 2.618 times, then in the transverse direction, it will decrease by 1.618 times. Here, the transverse direction coincides with the direction of movement of the crack. It is easy to see the linearity of the dependence from which the increase in the average grain diameter is determined. It follows, that with uniform uniaxial plastic deformation, the critical opening at the crack tip should also decrease linearly, depending on the relative elongation 𝑒𝑧. When rolling steel sheets, such a pronounced linear relationship is not detected. Obviously, this is due to transverse deformations, which are characterized by flattened grains.
. That is, if the average diameter increases in the longitudinal direction by 2.618 times, then in the transverse direction, it will decrease by 1.618 times. Here, the transverse direction coincides with the direction of movement of the crack. It is easy to see the linearity of the dependence from which the increase in the average grain diameter is determined. It follows, that with uniform uniaxial plastic deformation, the critical opening at the crack tip should also decrease linearly, depending on the relative elongation 𝑒𝑧. When rolling steel sheets, such a pronounced linear relationship is not detected. Obviously, this is due to transverse deformations, which are characterized by flattened grains.
Diagrams of the change of 𝐾𝐾1𝑐𝑐 as a function of δ for steels (Table 1) are shown in Fig. 2.
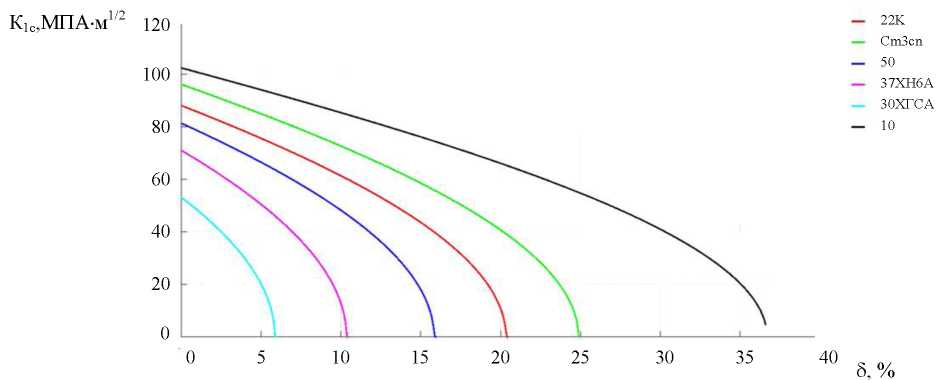
Fig. 2. Change in crack resistance depending on the preliminary elongation of steels
The critical intensity coefficient is calculated from (14) using the data in Table 1. This enables to determine the level of 𝐾1𝑐 under plastic deformation through pulling and compare it to the values of other steels. Thus, the comparison of 30HGSA steel treated to yield strength σт = 1360 MPa, and steel 10 shows that when using low-strength steel 10, level 𝐾1𝑐 can be reduced only with large elongation deformations (about 25 %). In practice, this happens quite rarely in constructions. However, with targeted pulling or cold rolling, a significant decrease in 𝐾1𝑐, is possible, and this should be taken into account.
If to rank steels according to the ultimate plasticity and compare maximum values of 𝐾1𝑐 for them, it turns out that plasticity decreases from one steel grade to another much faster than the critical stress intensity coefficient changes. So, 𝐾1𝑐 for 30HGSA and 10 steels, in the initial state of delivery differs by  2 times, and relative elongation δ — by
2 times, and relative elongation δ — by  5 times. The appearance of plasticity in the tops of various stress concentrators is inevitable, therefore, to provide the necessary reliability of elements made of 30HGSA steel, it is advisable to control plastic deformations in the structure
5 times. The appearance of plasticity in the tops of various stress concentrators is inevitable, therefore, to provide the necessary reliability of elements made of 30HGSA steel, it is advisable to control plastic deformations in the structure  5 times more precisely. In addition, it should be taken into account that a decrease in viscosity by
5 times more precisely. In addition, it should be taken into account that a decrease in viscosity by  2 times will cause a decrease in the critical crack length by
2 times will cause a decrease in the critical crack length by  4 times. The reason is the low viscosity and ductility of 30HGSA steel, for whose operation it will be required to increase the safety factor by
4 times. The reason is the low viscosity and ductility of 30HGSA steel, for whose operation it will be required to increase the safety factor by  5 times. The latter does not mean that high-strength steels as a structural material are worse than medium-strength steels. The problem is in selecting the optimal combination of viscosity, ductility, and strength. The calculated dependences obtained in this analysis make it possible to evaluate these characteristics by calculation. This is important for the rational choice of material at the design stage, determining the optimal welding and heat treatment modes.
5 times. The latter does not mean that high-strength steels as a structural material are worse than medium-strength steels. The problem is in selecting the optimal combination of viscosity, ductility, and strength. The calculated dependences obtained in this analysis make it possible to evaluate these characteristics by calculation. This is important for the rational choice of material at the design stage, determining the optimal welding and heat treatment modes.
Let us compare the results of calculations according to (18) with the known dependence (7)8 (fig. 2). The first function depends on the remaining ductility of the steel, and the second — on the relative length of the crack in the concept of the structural element. To conveniently present the results for their comparison, we introduce a dimensionless parameter:
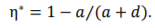 (20)
(20)
Fig. 3. Dependences of the relative crack resistance limit on the dimensionless parameter of the disc-shaped crack η∗ and on the dimensionless parameter of the preliminary uniform elongation of the material δ∗. Lines are analytical dependences (7), (18). Markers are experimental data for compact sample9 [11, 16] with dimensions b
After substituting (20) into (7), we obtain an invariant expression for the mean value. If we know η∗, then we can find the relation 𝑎⁄(𝑎 + 𝑑) from (20). The comparison results show that the functions are almost the same. In relative coordinates, they are characterized by invariance with good approximation. Both functions well approximate the experimental data of the crack resistance limit obtained on the samples with characteristic dimensions 𝑏𝑏 [13].
Consider the conditions of plane deformation at the known critical crack length 𝐿c. For hypopearlitic steels with σт < 400 MPa, it can be estimated approximately as 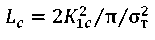 , and it is easy to find the critical voltage of the external load
, and it is easy to find the critical voltage of the external load 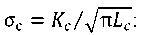
 (21)
(21)
The equation reflects the law of reduction of critical stresses σc below the value of the endurance limit of a material with crack length 𝐿𝑐 depending on the amount of preliminary elongation of the material. In the same formulation, the decrease in the critical crack length in the pre-deformed soft interlayer material can be estimated from the dependence:
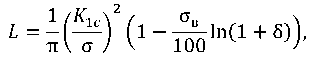 (22)
(22)
where 𝐿 — half the length for through crack; σ — critical stress for catastrophic crack propagation with length 𝐿.
At σ = σ−1, it follows from (22) that length 𝐿 of the catastrophic crack propagation is directly proportional to the value 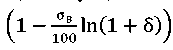 and the constant of the soft interlayer material 𝐿𝑐.
and the constant of the soft interlayer material 𝐿𝑐.
The obtained dependences in the system aggregate represent the proposed mathematical model for assessing the crack resistance of welded joints with soft interlayers.
Discussion and Conclusions. When welding heat-strengthened steels for hull and other sheet structures, soft interlayers are formed, the metal of which is plastically deformed in the first loading cycles. Numerical analysis methods using CAE tools10 can determine deformations or an increase in the width of the soft interlayer of the welded joint under the action of workloads. The reliability of the connection with a soft layer depends on the degree of plastic deformation, its hardening, stiffness of stress state with account of the boundary zones of the hard layers, and when a crack appears — on its critical length 𝐿. When pulling the soft interlayer, 𝐿 decreases in direct proportion to the constant of the soft interlayer material 𝐿𝑐 and the expression depending on the degree of pulling δ, i.e., on the relative pre-elongation.
A simple analytical dependence of the critical elongation to fracture is obtained (19). It provides calculation results that are in satisfactory agreement with experimental data for most structural steels (as of delivery). The formula provides estimating the reference characteristic δ5 of the sample by the only known parameter — the ultimate limit of strength. This dependence is characterized by a theoretical regularity that is in good agreement with th e parameters of structural steels. However, in some cases (special heat treatment or tempering modes), it can give a relative error up to  30 − 40 %.
30 − 40 %.
Analytical dependence of the change in the crack resistance limit of a soft interlayer on its preliminary plastic deformation is proposed. Compared:
- calculated values of the crack resistance limit;
- experimental data obtained on compact test samples;
- earlier analytical solutions.
The comparison results convincingly prove the applicability of the proposed analytical solution. The effect of the law of reducing the crack resistance limit with relative preliminary plastic elongation up to destruction (δ5) and a change in parameter (η∗) of a pregrown crack in the material up to 𝐿𝑐 are studied. For this case, invariance in relative coordinates is established under the condition of plane deformation and the absence of the influence of the limited size of the sample or structure. Consideration of the limited size of samples and different loading schemes significantly changes the mentioned dependence11 [13, 17].
The method proposed for estimating the crack resistance limit of welded elements with soft interlayers can be used in engineering calculations to minimize metal consumption, as well as for ship structures subjected to low-cycle fatigue.
1. Matokhin GV, Molokov KA. Prochnost' i nadezhnost' svarnykh soedinenii. Vladivostok: DVFU; 2019. 143 p. (In Russ.)
2. Matokhin GV, Molokov KA. Prochnost' i nadezhnost' svarnykh soedinenii. Vladivostok: DVFU; 2019. 143 p. (In Russ.)
3. Goldstein RV, Morozov NF. Mekhanika deformiruemogo tverdogo tela: problemy i rezul'taty. In: Proc. All-Russian Conf. in memory of Academician L.I. Sedov on the centenary of his birth. Moscow: Torus Press; 2009. P. 121–166. (In Russ.)
4. Matokhin GV, Molokov KA. Ibid.
5. Goldstein RV, Morozov NF. Ibid.
6. Molokov KA. Otsenka povrezhdennosti ferrito-perlitnykh stalei v usloviyakh malotsiklovogo nagruzheniya. In: Proc. Conf. “Nauka. Innovatsii. Tekhnika i tekhnologii: problemy, dostizheniya i perspektivy”. Komsomolsk-na-Amure: KnAGTU; 2015. P. 126–129. https://www.elibrary.ru/item.asp?id=25725387
7. Ibid.
8. Goldstein RV, Morozov NF. Ibid.
9. Matokhin GV, Molokov KA. Ibid.
10. CAE (computer-aided engineering). This is the name of programs and software systems for solving engineering problems.
11. Goldstein RV, Morozov NF. Ibid.
References
1. Повреждения и расчетный анализ прочности корабельных конструкций / В. В. Новиков, Г. П. Турмов, О. Э Суров [и др.]. — Владивосток : ДВФУ, 2020. — 266 с.
2. Махутов, Н. А. Деформационные критерии разрушения и расчет элементов конструкций на прочность / Н. А. Махутов. — Москва : Машиностроение, 1981. — 272 с.
3. Компьютерное моделирование контактного упрочнения алюминиевой прослойки магниево- алюминиевых цилиндрических сосудов / Л. М. Гуревич, Ю. П. Трыков, И. А. Пономарева, В. Н. Арисова // Вестник Сибирского государственного индустриального университета. — 2015. — № 4 (14). — С. 12–16.
4. Айметов, С. Ф. Прочность стыковых сварных соединений, ослабленных мягкой прослойкой, при действии изгибающей нагрузки / С. Ф. Айметов, Ф. Г. Айметов // Вестник Южно-Уральского государственного университета. — 2015. — Т. 15, № 1. — С. 107–112. — (Металлургия).
5. Влияние неоднородности механических совйств различных зон сварного стыкового соединения на работу соединения в упругопластической стадии деформации / В. И. Берг, М. Н. Чекардовский, С. В. Якубовская, В. С. Торопов // Современные проблемы науки и образования : [сайт]. — 2015. — № 2/3. — 28 с. — URL: http://www.science-education.ru/ru/article/view?id=23518 (дата обращения: 11.02.2021).
6. Кулиев, В. Д. Разрушение многослойных материалов с усталостной трещиной / В. Д. Кулиев, Ю. В. Зайцев, П. С. Султыгова // Известия Казанского государственного архитектурно-строительного университета. — 2014. — № 3 (29). — С. 162–166.
7. Оценка надежности судовых конструкций с микротрещинами и остаточными сварочными напряжениями / К. А. Молоков, В. В. Новиков, Г. П. Турмов, Н. П.Васильченко // Морские интеллектуальные технологии. — 2018. — Т. 1, № 3 (41). — С. 45–54.
8. Молоков, К. А. Оценка поврежденности феррито-перлитных сталей при перегрузках / К. А. Молоков, А. В. Славгородская // Морские интеллектуальные технологии. — 2013. — № 2. — C. 56–58.
9. Бирдегулов, Л. Р. Исследование трещиностойкости металлов / Л. Р. Бирдегулов, А. М.Щипачев // Juvenis scientia. — 2016. — № 2. — C. 28–32.
10. Аснис, А. Е. Динамическая прочность сварных соединений из малоуглеродистой и низколегированной сталей / А. Е. Аснис. — Москва ; Киев : Машгиз, 1962. — 171 с.
11. Матвиенко, Ю. Г. Двухпараметрическая механика разрушения / Ю. Г. Матвиенко. — Москва : Физматлит, 2021. — 208 с.
12. — Матохин, Г. В. Оценка ресурса сварных конструкций из феррито-перлитных сталей / Г. В. Матохин. Владивосток : ДВГТУ, 2001. — 202 с.
13. Прочность, ресурс, живучесть и безопасность машин / Отв. ред. Н. А. Махутов. — Москва : Либроком, 2008. — 576 с.
14. Зоны локализации пластической деформации в предварительно деформированных тонколистовых пластичных материалах / В. Ю. Гольцев, А. В. Зеленский, О. Г. Кудрявцев, Ю. Г. Матвиенко // Исследование прочности материалов и конструкций атомной техники. — Москва : Энергоатомиздат, 1984. — С. 68–73.
15. Научные основы повышения малоцикловой прочности / Н. А. Махутов, К. В. Фролов, М. М. Гаденин [и др.] ; под ред. Н. А. Махутова. — Москва : Наука, 2006. — 623 с.
16. Сосновский, Л. А. Трещиностойкость / Л. А. Сосновский, А. В. Богданович. — Гомель : БелГУТ, 2011. — 366 с.
17. Математические модели оценки эксплуатационного ресурса и работоспособности судовых сварных конструкций / К. А. Молоков, В. В. Новиков, Г. П. Турмов, А. С. Владимирович. — Владивосток : Дальневосточный федеральный университет, 2021. — 240 с.
About the Authors
K. A. MolokovRussian Federation
Vladivostok
V. V. Novikov
Russian Federation
Vladivostok
Review
For citations:
Molokov K.A., Novikov V.V. Evaluation of crack resistance of welded joints with soft interlayers. Advanced Engineering Research (Rostov-on-Don). 2021;21(4):308-311. https://doi.org/10.23947/2687-1653-2021-21-4-308-318
JATS XML














































