О неоднозначности механической мощности

Введение. Механическая энергия бывает обратимой (потенциальная и кинетическая), а также необратимой (например, тепловая при трении). Временную производную от последней принимают за механическую мощность. Отметим, что в силу необратимости тепловой энергии ее производная принимает только положительные значения. Вместе с тем производные получают как от потенциальной, так и от кинетической энергии. Особый интерес представляют гармонические колебания [1–4], при которых производные (мгновенные мощности) будут знакопеременными функциями, что принципиально отличает их от тепловой мощности.

Аналог кинетической энергии в электротехнике — энергия магнитного поля катушки индуктивности, аналог потенциальной энергии — энергия электрического поля конденсатора, а аналог механической тепловой энергии — тепловая же энергия, рассеиваемая резистором. Механические колебания широко распространены в разнообразных технологических процессах [5–8]. Приводы машин и механизмов преимущественно электромеханические [9–12], поэтому механическая реактивная мощность трансформируется в электрическую реактивную мощность сети, ухудшая качество электроэнергии [13]. В этой связи учет механической реактивной мощности имеет немаловажное значение [14], и этим обусловлена актуальность представленной работы.

Материалы и методы. Рассмотрены механические мощности при гармонических колебаниях. В качестве литературной базы изучены отечественные и зарубежные источники, в которых освещаются вопросы динамики, кинематики, вибраций, преобразования движения в колебательных системах и т. п. Используются теоретические (преимущественно математические) методы исследования.

Результаты исследования

Мощность, развиваемая при вынужденных гармонических колебаниях инертного тела. Движение тела описывается известным выражением:

x=l sinwt

Соответственно, скорость:

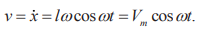
Для гармонической величины действующее значение меньше амплитудного в 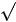2 :

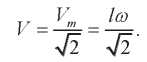(1)

Формула для силы имеет вид:

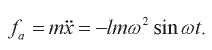(2)

Формула для силы трения:

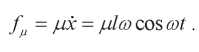(3)

Результирующая сила:

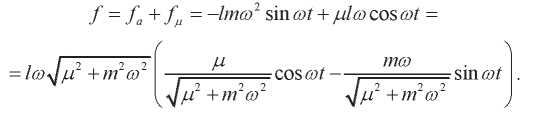
Обозначим:

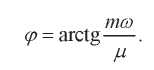(4)

С учетом этого:

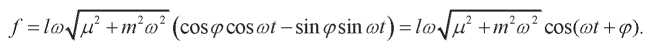
Очевидно, что

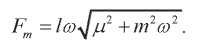
Действующее значение результирующей силы:

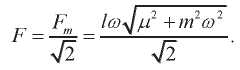 (5)

Мгновенная результирующая мощность:

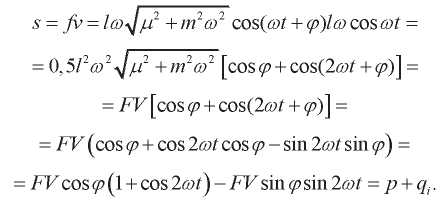 (6)

В электротехнике есть выражение, аналогичное (6), с заменами F → U V → I. Из него определяют активную мощность:

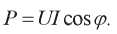
Поэтому активную (тепловую) механическую мощность тоже следует определить, как:

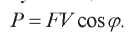 (7)

Очевидно, что гармонические сила и скорость совершают колебания со сдвигом фаз, равным .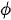

Из вышеназванной формулы электротехники определяют реактивную мощность:

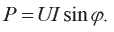
Поэтому реактивную (инерционную) механическую мощность тоже следует определить, как:

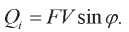(8)

Из (6) следует, что под активной мощностью понимается среднее за полпериода значение мгновенной мощности, а под реактивной — амплитудное значение. В электротехнике аналогично.

Еще одно обобщение из электротехники — полная механическая мощность:

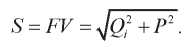(9)

Она примечательна тем, что, с одной стороны, описывается формулой Пифагора, а с другой — равна
произведению действующих значений гармонических величин.
Имея в виду (1), (5) и (8),

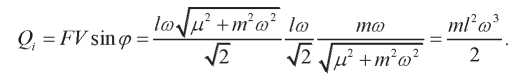(10)

При этом:

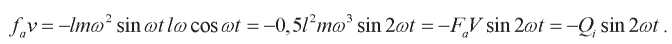(11)

Это соответствует выражениям (6) и (10).

Имея в виду (1), (5) и (7),

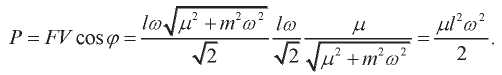(12)

При этом:

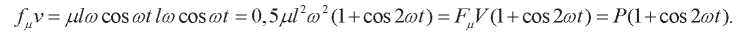 (13)

Это соответствует выражениям (6) и (12).

Имея в виду (9), (10) и (12),

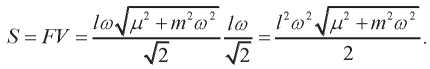
Мощность, развиваемая при упругих деформациях. Выражение для силы имеет вид:

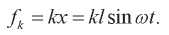(14)

С учетом (3) результирующая сила равна:

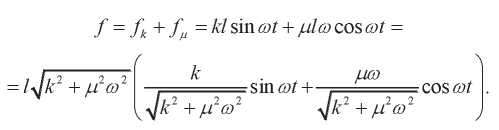
Обозначим:

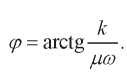
Значит,

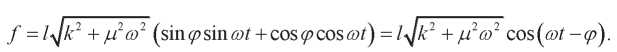
Очевидно, что:

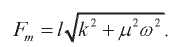
Действующее значение результирующей силы равно:

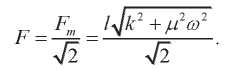 (15)

Мгновенная результирующая мощность:

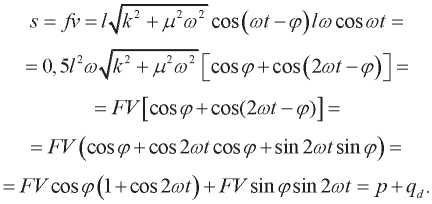 (16)

Имея в виду (6), (7) и (12), активная механическая мощность равна:

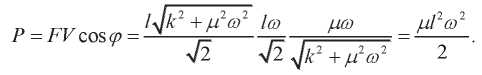
Принимая во внимание (15), (1), (8) и (16), механическая реактивная (упругая) мощность равна:

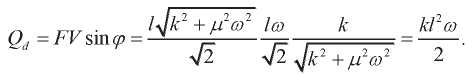(17)

При этом:

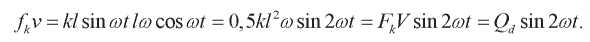(18)

Это соответствует выражениям (16) и (17).

Очевидно, что полная мощность равна:

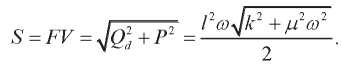
Мощность при колебаниях, связанных с гравитационным воздействием. При отклонении подвешенного груза на угол 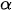возникает момент:

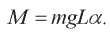
Пусть

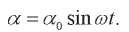
Тогда

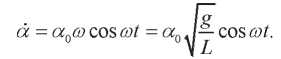
Мгновенная мощность имеет вид:

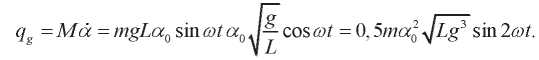
Ее амплитуда и, соответственно, реактивная мощность гравитационного воздействия определяется, как:

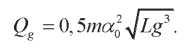
Реактивная, активная и полная мощности в комплексном представлении. В [15] показано, что при инертной нагрузке:

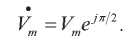
Мгновенная скорость при этом равна:

Формулы для действующих значений величин принципиально не отличаются:

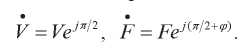
В электротехнике подробно описана особенность комплексного представления: при вычислении полной мощности один из перемножаемых векторов должен быть сопряженным.

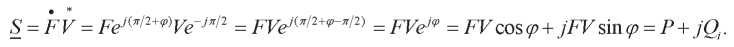
Это выражение для инертной нагрузки. Упругая нагрузка отличается тем, что реактивная мощность имеет противоположный знак:

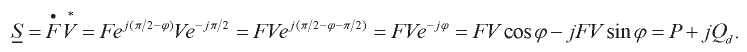
При этом:

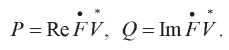
Механические мощности в векторном представлении. В основе комплексного представления лежит идея вращающихся в комплексной плоскости векторов. Тот же принцип может быть реализован в трехмерном Декартовом базисе.

Из (7)–(9) следует:

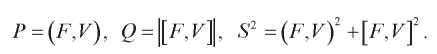
Математическая абстракция с проекциями вращающихся векторов имеет конкретную материальную основу в виде кривошипно-кулисных механизмов.

Обсуждение и заключения. Математическими методами исследованы мощности:

• при вынужденных гармонических колебаниях инертного тела,
• при упругих деформациях,
• при колебаниях, связанных с гравитационным воздействием,
• реактивная, активная и полная (в комплексном представлении),
• механическая (в векторном представлении).

Показано, что при механических гармонических колебаниях развивается не только знакоположительная тепловая мощность, но и знакопеременные реактивные мощности, характеризующие обратимость кинетической и потенциальной энергий.

При этом полная механическая мощность удовлетворяет формуле Пифагора.

Представление о механических реактивных, активной и полной мощностях является обобщением соответствующих понятий о мощностях из электротехники, и таким образом проявляется электромеханический дуализм.