On the ambiguity of mechanical power

Introduction. Mechanical energy can be reversible (potential and kinetic), as well as irreversible (e.g., thermal in friction). The time derivative of the latter is taken as mechanical power. Note that due to the irreversibility of thermal energy, its derivative takes only positive values. At the same time, derivatives are obtained from both potential and kinetic energy. Of particular interest are harmonic vibrations [1–4], where derivatives (instantaneous powers) will be alternating functions, which fundamentally distinguishes them from thermal power.

The analogue of kinetic energy in electrical engineering is the magnetic field energy of the inductor, the analogue of potential energy is the capacitor electric field energy, and the analogue of mechanical thermal energy is the thermal energy dissipated by the resistor.

Mechanical vibrations are widespread in various production processes [5–8]. The drives of machines and mechanisms are mainly electromechanical [9–12], therefore, mechanical reactive power is transformed into electrical reactive power of the network, impairing the quality of electricity. In this regard, accounting for mechanical reactive power is of no small importance [14], and this determines the urgency of the presented study.

Materials and Methods. Mechanical power under harmonic vibrations is considered. As a literary basis, domestic and foreign sources, which cover the issues on dynamics, kinematics, vibrations, transformation of motion in oscillatory systems, etc., have been studied. Theoretical (mainly mathematical) research methods are used.

Research Results

The power developed by forced harmonic vibrations of an inert body. The body motion is described by the well-known expression:

x = l sinwt .

Accordingly, the speed:

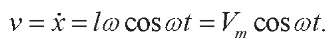
For harmonic quantity, the effective value is less than the amplitude in 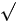2 :

(1)

Formula for the force is:

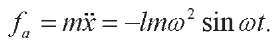(2)

Formula for friction force is:

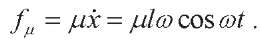(3)

Resultant force is:

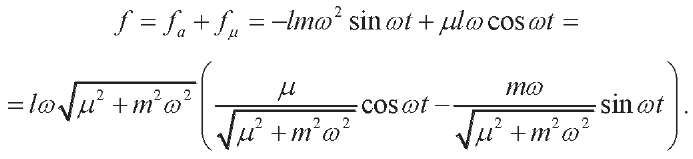
Denote:

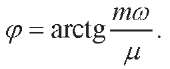(4)

With this in mind:

Obviously,

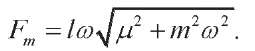
The effective value of the resultant force:

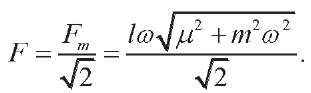(5)

Instantaneous resultant power:

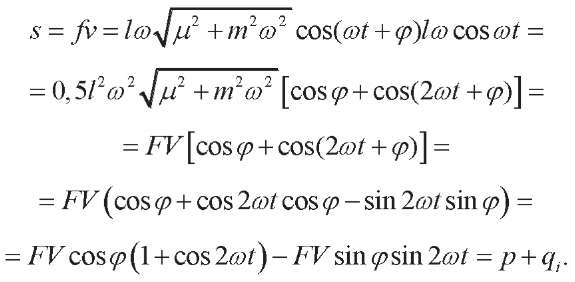(6)

In electrical engineering, there is an expression similar to (6), with substitutions F → U V → I. The active power is determined from it:

P =UI cosj

Therefore, the active (thermal) mechanical power should also be defined as:

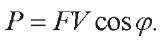(7)

It is obvious that the harmonic force and velocity vibrate with a phase shift equal to j .

From the above-mentioned formula of electrical engineering, the reactive power is determined:

P =UI sinj.

So, reactive (inertial) mechanical power should also be defined as:

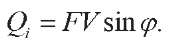(8)

It follows from (6) that the active power is the half-period average of the instantaneous power, and the reactive power is the amplitude value. In electrical engineering, it is similar.

Another generalization from electrical engineering is total mechanical power:

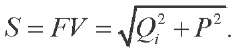(9)

It is remarkable in that, on the one hand, it is described by the Pythagorean formula, and on the other hand, it is equal to the product of the effective values of harmonic quantities.

With a view to (1), (5) and (8),

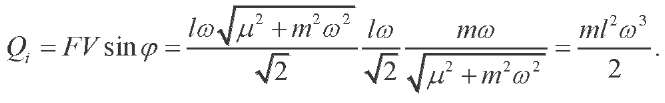(10)

Here:

(11)

This corresponds to expressions (6) and (10).

Keeping in view (1), (5) and (7),

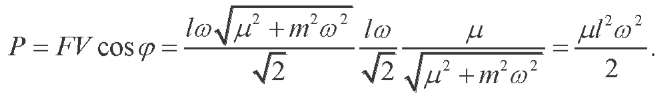(12)

In addition:

(13)

This corresponds to expressions (6) and (12).

Having in view (9), (10) and (12),

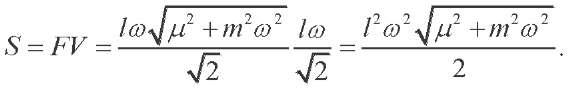
The power developed under elastic deformations. The expression for the force is:

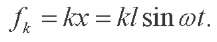(14)

Taking into account (3), the resultant force is:

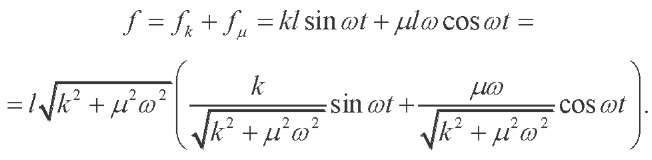
Denote:

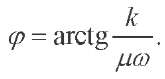
Hence,

It is obvious that:

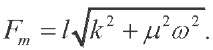
The effective value of the resultant force is equal to:

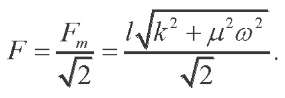(15)

Instantaneous resultant power is:

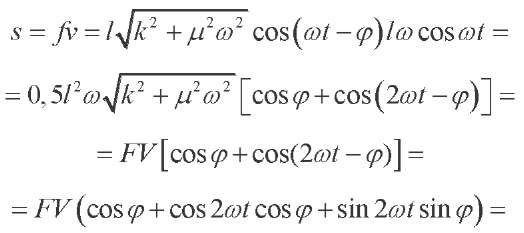
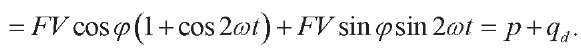(16)

Bearing in mind (6), (7) and (12), the active mechanical power is equal to:

Taking into account (15), (1), (8) and (16), the mechanical reactive (elastic) power is equal to:

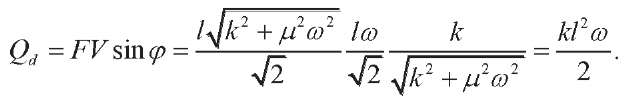(17)

Here:

(18)

This corresponds to expressions (16) and (17).

Obviously, the total power is:

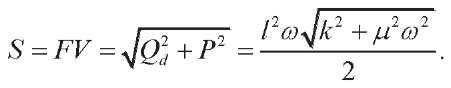
Power during vibrations associated with gravitational influence. When the suspended load is deflected by

angle a, the moment occurs:

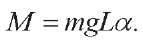
Suppose

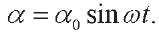
Then

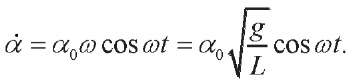
Instantaneous power has the form:

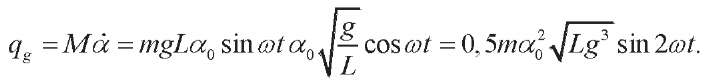
Its amplitude and, accordingly, the reactive power of the gravitational effect is defined as:

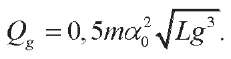
Reactive, active and total power in a complex representation. In [15], it is shown that under an inert load,

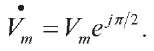
In this case, the instantaneous speed is equal to:

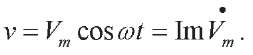
Formulas for the effective values are not fundamentally different:

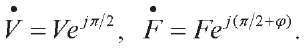
In electrical engineering, a feature of the complex representation is described in detail: when calculating the total power, one of the multiplied vectors must be conjugate.

This is an expression for an inert load. The elastic load differs in that the reactive power has the opposite sign:

Here:

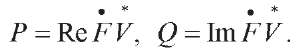
Mechanical powers in vector representation. The complex representation is based on the concept of vectors rotating in the complex plane. The same principle can be implemented in a three-dimensional Cartesian basis.

From (7)–(9), it follows:

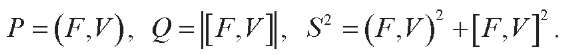
Mathematical abstraction with projections of rotating vectors has a specific material basis in the form of slot-and-crank mechanisms.

Discussion and Conclusions. Mathematical methods were used to study the following powers:

• under forced harmonic vibrations of an inert body,
• under elastic deformations,
• under vibrations associated with gravitational action,
• reactive, active and total (in complex representation),
• mechanical (in vector representation).

It is shown that under mechanical harmonic vibrations, not only sign-positive thermal power develops, but also alternating reactive powers characterizing the reversibility of kinetic and potential energies.

At the same time, the total mechanical power satisfies the Pythagorean formula.

The idea of mechanical reactive, active and total powers is a generalization of the corresponding concepts of power from electrical engineering, and thus, electromechanical dualism manifests itself.