Scroll to:
Application of an Inertial Sensor Unit for Position Estimation and Motion Control of the Lower-Extremity Powered Exoskeleton
https://doi.org/10.23947/2687-1653-2022-22-3-204-213
Abstract
Introduction. The problem of controlling the lower-extremity powered exoskeleton motion was investigated. To solve it, it was proposed to use a program control and feedback control. The formation of control in the form of feedback required an assessment of the state of the exoskeleton (rotation angles, angular velocities, and accelerations of the links). The possibility of using an inertial measuring unit to estimate angular velocities and accelerations of exoskeleton links was considered. The work objective was to develop laws for the formation of the exoskeleton motion control, which could provide the stability of the program motion and use the measurements of encoders, micromechanical gyroscopes and accelerometers.
Materials and Methods. Previously performed mathematical modeling of the exoskeleton dynamics was used to form a program control. It was proposed to equip the exoskeleton with inertial sensor units. This solution made it possible to evaluate the state vector of the exoskeleton and to use these estimates in a feedback loop. A mathematical model of measurements of these sensors was described. The proposed version is suitable for control systems of three-link exoskeletons of the lower extremities and can be expanded to the case of multi-link exoskeleton designs.
Results. New laws of exoskeleton motion control based on a mathematical model of the system dynamics and using measurement information from encoders and inertial information sensors were proposed. Numerical simulation of exoskeleton motion was performed in the Wolfram Mathematica mathematical package. Its results confirmed the operability of the proposed control and the possibility of using an inertial sensor unit to assess the exoskeleton state. The numerical simulation results for the following program movements were presented: lifting the exoskeleton from a sitting position to a vertical position, and stabilization of the vertical equilibrium position.
Discussion and Conclusions. The proposed control can be applied in exoskeletons for medical purposes, e.g., in the task of verticalization of patients with dysfunctions of the musculoskeletal system. The possibility of using measurement information obtained from inertial measurements units in the problem of estimating the state of exoskeleton links was demonstrated. The use of inertial sensors will make it possible to determine the angular acceleration of the exoskeleton links, avoiding numerical differentiation of the measurement information received from the encoders. The obtained estimates of angular acceleration allow us to introduce feedback on angular accelerations into the control system, which opens up the possibility of improving transients in controlling the exoskeleton motion.
For citations:
Saypulaev G.R., Saypulaev M.R., Merkuryev I.V., Adamov B.I., Garcia R.B. Application of an Inertial Sensor Unit for Position Estimation and Motion Control of the Lower-Extremity Powered Exoskeleton. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):204-213. https://doi.org/10.23947/2687-1653-2022-22-3-204-213
Introduction. The development of devices designed to facilitate motion and increase motor efficiency (of exoskeletons) is perspectives for development robotics.
Exoskeletons are increasingly used in industry [1], military [2], medicine [3], and other fields. This specifies topicality of the research on their circuit and structural design, energy consumption optimization, motion trajectory, dynamics, control.
The present paper considers an active lower-extremity powered exoskeleton of a human with a rigid structure of the load-bearing frame. It is used for the rehabilitation of the musculoskeletal patients.
The development of such exoskeletons requires solving interrelated scientific and technical problems. They include:
- formation of a skeletal scheme;
- mathematical modeling of exoskeleton motion [4–6];
- optimization of the links motion based on a mathematical model of kinematics and dynamics1;
- reasonable construction of the motor system [7][8];
- reasonable construction of the motor system [9–11] and estimation [13][14].
All of the above tasks are connected by the problem of finding control actions for program motion. Firstly, their source may be the dynamic model of the system. Secondly, they are developed in the form of a proportional integral-differential (PID) controller used to stabilize the program motion. A combination of two methods is also possible. At that, for the formation of feedback control (in particular, in the form of a PID controller), algorithms for assessing the state of a dynamic system and a set of sensors whose indicators are used in algorithms, play an important role.
To obtain information about the position of the exoskeleton links, they are equipped with an encoder or gyroscope [9–14]. Other possible options include accelerometer, magnetometer, potentiometer, sensors of torque, force, biosignals, etc.
In [13], it is proposed to use one block of inertial sensors consisting of gyroscopes and accelerometers on each link of the exoskeleton. This solution will provide estimating the angles of rotation, angular rates and accelerations. At the same time, the measurement model turns out to be nonlinear, which complicates the structure of control and monitoring systems.
The study aimed at improving the control of the exoskeleton by using two inertial blocks attached to each link of the exoskeleton. This approach enables to estimate the rotation angles, angular rates, and accelerations of the exoskeleton. With the help of the proposed arrangement of gyroscopes and accelerometers, a linear measurement model can be obtained, which will open up ways to simplify the control system and apply the theory of optimal evaluation of linear systems [15]. This, in turn, will be the basis for improving the motion control of the exoskeleton. The criterion for improving the control quality is reducing the deviations of the angular rates of the links from the program movement.
Materials and Methods. Consider the kinematic scheme of an exoskeleton with a rigid structure of the power frame with symmetrical movement of the legs in the sagittal plane (Fig. 1).
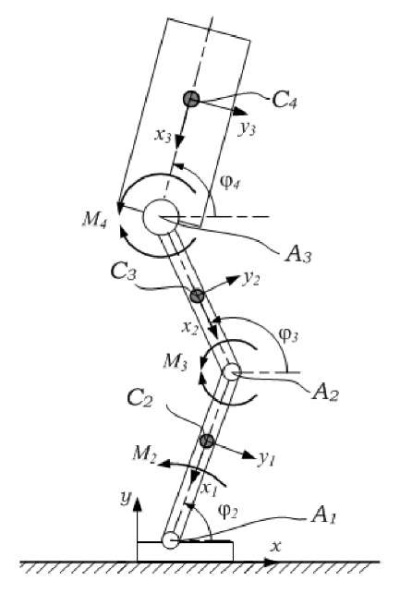
Fig. 1. Kinematic diagram of the lower-extremity powered exoskeleton in the sagittal plane
C2, C3, C4 — centers of mass of the lower legs, thighs and body, respectively; А1, А2, А3 — joints connecting the links of the exoskeleton; φ2, φ3, φ4 — rotation angles of the exoskeleton links; М2, М3, М4 — control moments created by the actuators located in the joints А1, А2, А3, respectively. Coordinate system xyz is introduced to describe the motion. x-axis is directed along the reference surface, y-axis is directed along the local vertical to the reference surface. z-axis complements the coordinate axes to the right Cartesian coordinate system.
As a basis for building an exoskeleton motion control system, we use a dynamic model from [6].
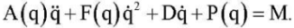 (1)
(1)
Here:
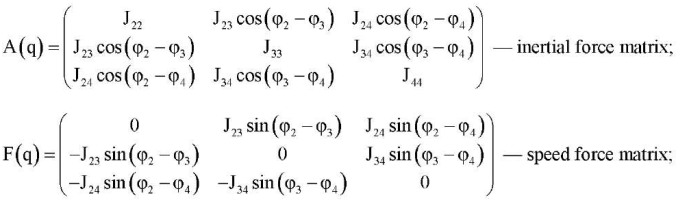
D = diag (μ2,μ3,μ4) — diagonal matrix of dissipative forces characterizing linear friction in joints;
P(q) = (MG2 cosφ2 MG3 cosφ3 MG4 cosφ4)T — column vector of moments arising from the action of gravity; M = (M2 – M3 M3 – M4 M4)T — column vector of control torques generated by actuators located in the joints of the exoskeleton links; q = (φ2, φ3, φ4)T — column vector of generalized coordinates, consisting of rotation angles of exoskeleton links; Jjk ( j, k = 2, 3, 4) — moments of inertia of exoskeleton links; μk (k = 2, 3, 4) — coefficients of linear friction in the joints of the exoskeleton links; MGk (k = 2, 3, 4) — maximum values of the moments of gravitational forces perceived by the output links of the drives.
Let the laws of change of angles and their derivatives be given for program motion:
 (2)
(2)
To control the exoskeleton motion, it is proposed to create control actions in the form of a sum of control moments:
- with software management
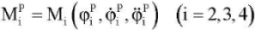 ;
; - PID controller
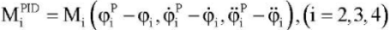
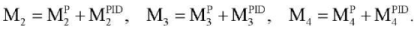 (3)
(3)
For program control, the values of control actions MiP can be calculated using the formulas [7]:
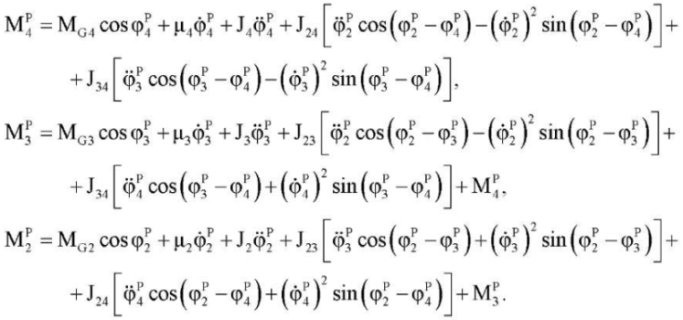 (4)
(4)
Values MiPID are calculated according to the feedback principle (in the form of a PID controller):
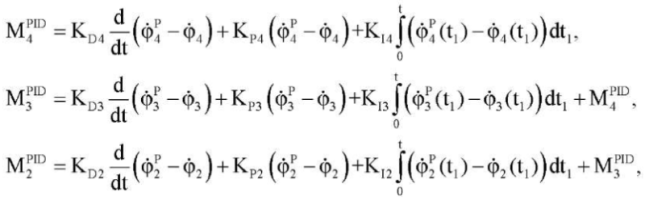 (5)
(5)
or
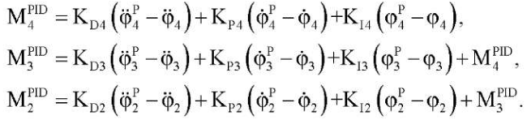 (6)
(6)
Here, the coefficients of the PID controller KPi, Kit, KDi (i = 2, 3, 4) can be:
- constant (they are found from the stability conditions);
- time functions (found from solving optimal control problems [9][13].
One of the problems of creation of control actions in the form of a PID controller is possible errors in the differentiation of measurement information. To avoid them, we use:
- encoders (for measuring the current rotation angles φi of the exoskeleton links);
- inertial sensor blocks of micromechanical gyroscopes (for measuring angular rates
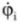 and accelerometers (for estimating angular rates
and accelerometers (for estimating angular rates 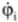 and accelerations
and accelerations 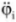 ).
).
The model for measuring rotation angles using encoders can be presented as:
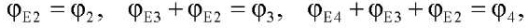 (7)
(7)
where φE2. φE3. φE4 — indications of encoders located in joints А1, А2, А3 (Fig. 1).
The model of angular rate measurements using micromechanical gyroscopes can be written as:
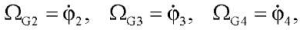 (8)
(8)
where ΩG2, ΩG3, ΩG4 — indications of gyroscopes attached to the links of the exoskeleton.
To estimate angular rate and accelerations using accelerometers, a pair of two-axis accelerometers can be used, which are located at opposite ends of each of the links. They measure the apparent accelerations associated with the corresponding links in projections on xiyi (i = 1, 2, 3).
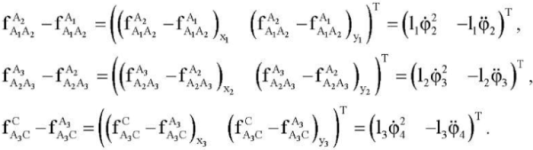 (9)
(9)
Here, 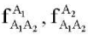 — vectors of readings of two-axis accelerometers mounted on link A1A2 and located at points A1 and A2, respectively;
— vectors of readings of two-axis accelerometers mounted on link A1A2 and located at points A1 and A2, respectively; 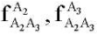 — vectors of readings of two-axis accelerometers mounted on link A2A3 and located at points A2 and A3, respectively;
— vectors of readings of two-axis accelerometers mounted on link A2A3 and located at points A2 and A3, respectively; 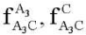 — vectors of readings of two-axis accelerometers mounted on link A3C and located at points A3 and C, respectively; l1 = |A1A2|, l2 = |A2A3|, l3 = |A3C| — distances between pairs of accelerometers attached to links A1A2, A2A3, and A3C, respectively.
— vectors of readings of two-axis accelerometers mounted on link A3C and located at points A3 and C, respectively; l1 = |A1A2|, l2 = |A2A3|, l3 = |A3C| — distances between pairs of accelerometers attached to links A1A2, A2A3, and A3C, respectively.
We combine equations (7)–(9) and write formulas for estimating the angles of rotation, angular rates, and accelerations:
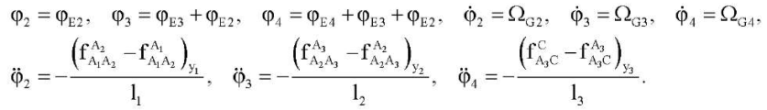 (10)
(10)
To correct estimates of angular speed modules, the equations can be used:
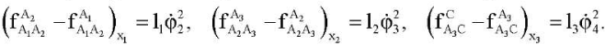 (11)
(11)
Thus, to estimate the rotation angles, angular rates and angular accelerations of the exoskeleton links, measurements can be processed with a moving average filter, Kalman filter algorithm, etc. [10][13][15].
In the simplest version of closing the feedback circuit when forming the control, we obtain expressions for the control moments:
 (12)
(12)
The introduction of angular acceleration feedback into the control system provides the diagonalization of the inertial forces matrix to reduce the cross-influence between generalized coordinates.
We simulate the exoskeleton motions to test the operability of the proposed control law. As a program motion, consider:
- change of position from sitting to standing [7];
- stabilization of the vertical position of the exoskeleton with initial deviations of the links from the vertical.
Research Results. For numerical simulation of the system, we took the parameters of the mathematical model of the exoskeleton from [6][7]. We considered a special case by choosing the same coefficients of the PID controller for each drive: 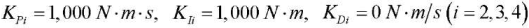 . Figure 2 shows the time dependences for the rotation angles and angular rates of the exoskeleton links. They were obtained at control moments corresponding to rising from a sitting position. As can be seen from Figure 2 a, at the end of the motion, the rotation angles of each link are equal φ2 = φ3 = φ4 = 90°, which corresponds to standing.
. Figure 2 shows the time dependences for the rotation angles and angular rates of the exoskeleton links. They were obtained at control moments corresponding to rising from a sitting position. As can be seen from Figure 2 a, at the end of the motion, the rotation angles of each link are equal φ2 = φ3 = φ4 = 90°, which corresponds to standing.
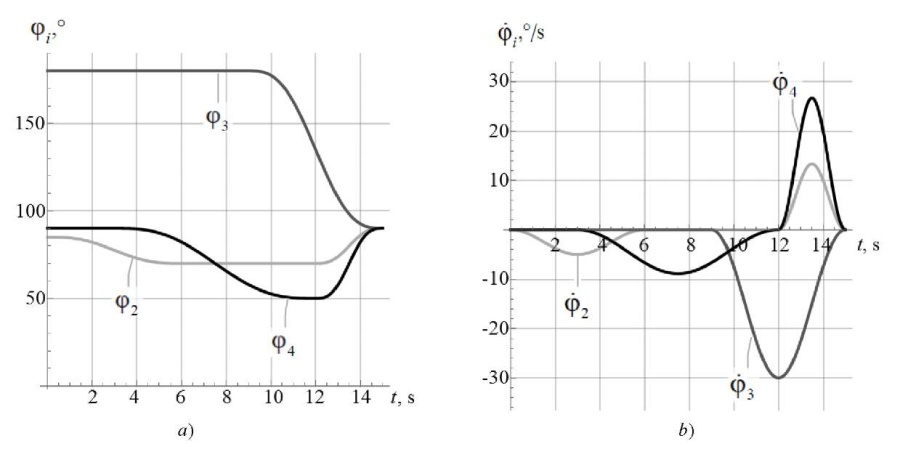
Fig. 2. Simulation results of rising from a sitting position
without initial deviations from the program motion
in the angles of rotation of the exoskeleton links:
a — rotation angles of the links;
b — angular rates of the links
Now let us consider the case with deviations of about 20° in the rotation angles of the links compared to the initial position set in the program motion. The simulation results of rising from a sitting position are shown in Figure 3. As in Figure 2, at the end of the motion time, the values of the rotation angles were equal to φ2 = φ3 = φ4 = 90°. Consequently, the use of a combination of software control and control in the form of a PID controller accurately brought the exoskeleton to the desired position.
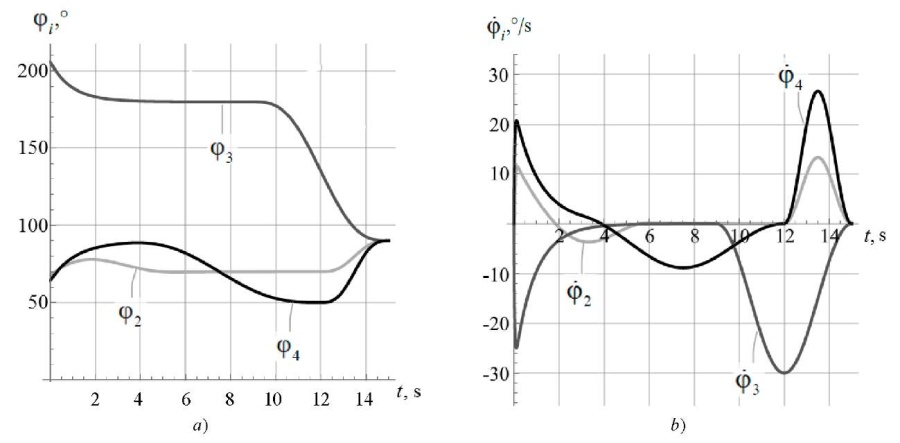
Fig. 3. Simulation results of rising from a sitting position
with initial deviations from the program motion
in the rotation angles of the exoskeleton links:
a — rotation angles of the links;
b — angular rates of the links
Thus, when modeling program motion, the operability of the proposed law of formation of control actions described in (4) and (12) was shown.
The vertical position of the exoskeleton is unstable without control; therefore, disturbing factors can cause deviations from equilibrium up to the falling of the exoskeleton.
We checked the operability of the proposed control in the task of stabilizing the vertical position of the exoskeleton. Values for the program motion were: 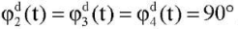 . We considered the case when there were deviations of about 20° from the vertical position in the rotation angles of the links (Fig. 4).
. We considered the case when there were deviations of about 20° from the vertical position in the rotation angles of the links (Fig. 4).
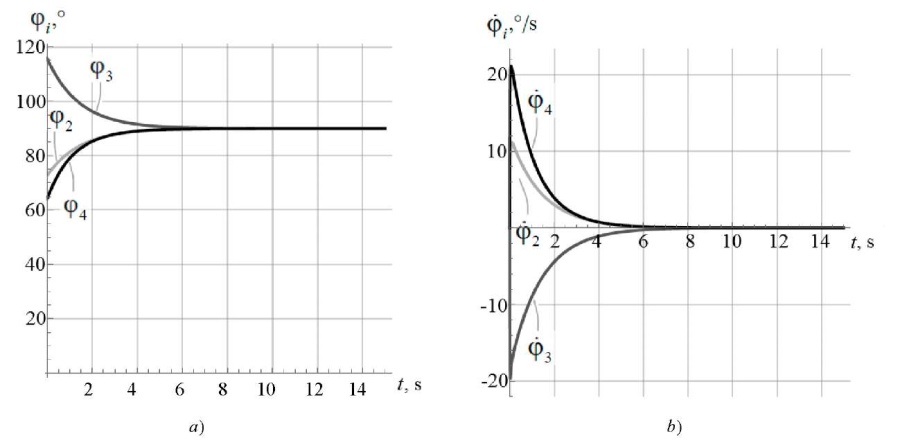
Fig. 4. Simulation results of stabilization of the vertical position
with initial deviations from the program motion
in the rotation angles of the exoskeleton links:
a — angles of rotation of the links;
b — angular rates of the links
Figure 4 shows that the proposed control provides stabilization of the vertical position of the exoskeleton links.
For comparison, we present the results of modeling the stabilization of the vertical position using the following values of the coefficients of the PID controller: 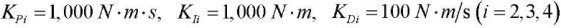 (Fig. 5).
(Fig. 5).
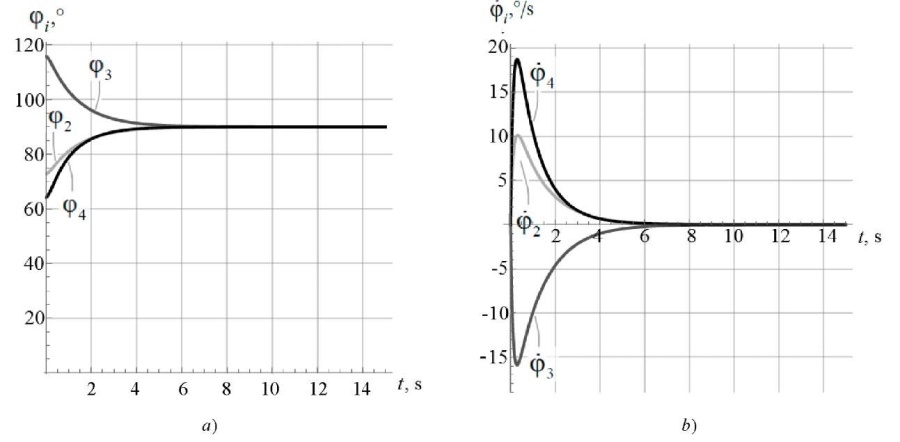
Fig. 5. Simulation results of stabilization of the vertical position
with initial deviations from the program motion
in the rotation angles of the exoskeleton links:
a — angles of rotation of the links;
b — angular rates of the links
It can be seen from Figure 5 that when using the differential link (KDi ≠ 0) of the regulator, it was possible to reduce emissions in the dependences of the angular rates of the exoskeleton links compared to the case KDi = 0 (Fig. 4 b).
Thus, the possibility of controlling the lower-extremity powered exoskeleton links using the readings of encoders and blocks of inertial sensors (micromechanical gyroscopes and accelerometers) was considered. The simulation results have validated this approach.
Discussion and Conclusions. The proposed solution to the problem of controlling the motion of the exoskeleton can be used in medical applications, including for the verticalization of musculoskeletal patients.
Thus, the data of the inertial sensor blocks can be used in the task of assessing the state of the exoskeleton links — their angular rates and accelerations. At the same time, there is no need for numerical differentiation of the measuring information of the encoders. Therefore, feedback on angular accelerations can be introduced into the control system, which makes it possible to improve transients when controlling the exoskeleton motion.
1. Yatsun SF, Savin SI, Yatsun AS, et al. Optimization of Time of Verticalization of the Exoskeleton by Criterion of Energy Efficiency. In: Vibratsionnye tekhnologii, mekhatronika i upravlyaemye mashiny. Pt. 2. Kursk: Izd-vo Yugo-Zap. gos. un-ta; 2016. P. 151–160. (In Russ.)
References
1. Exoskeletons for Industrial Application and Their Potential Effects on Physical Work Load / M. P. De Looze, T. Bosch, F. Krause [et al.] // Ergonomics. — 2015. — Vol. 59. — P. 671–681. https://doi.org/10.1080/ 00140139.2015.1081988
2. Геворкян, А. А. Роботизированная механотерапия: возможность применения экзоскелета для нижних конечностей у пациентов с нарушением функции ходьбы при рассеянном склерозе / А. А. Геворкян, С. В. Котов, В. Ю. Лиждвой // Альманах клинической медицины. — 2020. — Т. 48, № 1. — С. 7–12.
3. Экзоскелет — состояние проблемы и перспективы внедрения в систему абилитации и реабилитации инвалидов (аналитический обзор) / А. А. Воробьев, О. А. Засыпкина, П. С. Кривоножкина [и др.] // Вестник Волгоградского государственного медицинского университета. — 2015. — Вып. 2 (54). — С. 9–17.
4. Трехзвенная математическая модель для задачи стабилизации вертикальной позы человека / И. В. Новожилов, А. В. Терехов, А. В. Забелин [и др.] // Математическое моделирование движений человека в норме и при некоторых видах патологии. — Москва : Изд-во механико-математического факультета МГУ. — 2005. — С. 7–20.
5. Моделирование процессов вставания экзоскелета из положения сидя / С. И. Савин, С. Ф. Яцун, А. С. Яцун, Г. Я. Пановко // Проблемы машиностроения и надежности машин. — 2016. — Т. 3. — С. 19–24.
6. Saypulaev, M. R. Development of the Lower Extremity Exoskeleton Dynamics Model Using in the Task of the Patient Verticalization / M. R. Saypulaev, Yu. Yu. Zuev, G. R. Saypulaev // Journal of Physics: Conference Series. — 2021. — Vol. 2096. — Art. 0120421. https://doi.org/10.1088/1742-6596/2096/1/012042
7. Zuev, Yu. Yu. Laws of Motion of the Lower Extremities and Structural-parametric Synthesis of Electro-Hydraulic Executive Modules of the Active Exoskeleton According to the Criterion of Energy Sufficiency / Yu. Yu. Zuev, M. R. Saypulaev, V. Doni // Journal of Physics: Conference Series. — 2021. — Vol. 2096. — Art. 012044. 10.1088/1742-6596/2096/1/012044
8. Яцун, С. Ф. Определение параметров приводов биоинженерных мехатронных модулей для экзоскелета нижних конечностей человека / С. Ф. Яцун, А. Н. Рукавицин // Известия Юго-Западного государственного университета. — 2012. — Т. 2, № 1. — С. 196–200.
9. Savin, S. I. Energy-Efficient Algorithm of Control of Exoskeleton Verticalization / S. I. Savin, A. S. Yatsun, S. F. Yatsun // Journal of Machinery Manufacture and Reliability. — 2017. — Vol. 46. — P. 512–517.
10. A Robust Adaptive-Fuzzy-Proportional-Derivative Controller for a Rehabilitation Lower Limb Exoskeleton / N. Aliman, R. Ramli, S. M. Haris [et al.] // International Journal of Engineering Science and Technology. — 2022. — Vol. 35. — Art. 101097. 10.1016/j.jestch.2022.101097
11. Adaptive Particle Swarm Optimization of PID Gain Tuning for Lower-Limb Human Exoskeleton in Virtual Environment / M. S. Amiri, R. Ramli, M. F. Ibrahim [et al.] // Mathematics. — 2020. — Vol. 8. — Art. 2040. 10.3390/math8112040
12. Development and Control of an Electro-Hydraulic Actuator System for an Exoskeleton Robot / Dongyoung Lee, Buchun Song, Sang Yong Park, Yoon Su Baek // Applied Sciences. — 2019. — Vol. 9. — Art. 4295. 10.3390/app9204295
13. Lora-Millan, J. S. An IMUs-Based Extended Kalman Filter to Estimate Gait Lower Limb Sagittal Kinematics for the Control of Wearable Robotic Devices / J. S. Lora-Millan, A. F. Hidalgo, E. Rocon // IEEE Access. — 2021. — Vol. 9. — P. 144540–144554. 10.1109/ACCESS.2021.3122160
14. Minimizing Human-Exoskeleton Interaction Force by Using Global Fast Sliding Mode Control / Duong Mien Ka, Cheng Hong, Tran Huu Toan, Jing Qiu // International Journal of Control, Automation and Systems. — 2016. — Vol. 14. — P. 1064–1073. 10.1007/s12555-014-0395-7
15. Балакришнан, А. В. Теория фильтрации Калмана / А. В. Балакришнан. — Москва : Книга по требованию. — 2021. — 164 с.
About the Authors
G. R. SaypulaevRussian Federation
14, Krasnokazarmennaya St., Moscow
M. R. Saypulaev
Russian Federation
14, Krasnokazarmennaya St., Moscow
I. V. Merkuryev
Russian Federation
14, Krasnokazarmennaya St., Moscow
B. I. Adamov
Russian Federation
14, Krasnokazarmennaya St., Moscow
R. B. Garcia
Russian Federation
14, Krasnokazarmennaya St., Moscow
Review
For citations:
Saypulaev G.R., Saypulaev M.R., Merkuryev I.V., Adamov B.I., Garcia R.B. Application of an Inertial Sensor Unit for Position Estimation and Motion Control of the Lower-Extremity Powered Exoskeleton. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):204-213. https://doi.org/10.23947/2687-1653-2022-22-3-204-213
JATS XML














































