Scroll to:
Critical Loads of Uniformly Compressed Orthotropic Rectangular Plate on an Elastic Base
https://doi.org/10.23947/2687-1653-2022-22-3-214-223
Abstract
Introduction. The problem of critical loads of a compressed orthotropic rectangular plate on an elastic base was considered. The following orthotropy parameters were set for the plate: Poisson coefficients, Young's modules for the main directions, and the shear modulus of the plate material. The components of the compressive load were uniformly distributed along two opposite edges of the plate and acted parallel to the coordinate axes. The edges of the plate were loosely pinched or pivotally supported. Cases were also considered when two parallel edges of the plate were free from loads, and the other two were freely pinched or pivotally supported.
Materials and Methods. The problem was studied on the basis of a system of nonlinear Kármán-type equilibrium equations. The critical values of the load parameter were determined from a linearized problem based on a trivial solution. At the same time, the variational method in combination with the finite difference method was used to solve the boundary eigenvalue problem.
Results. The problem was reduced to solving a parametric linear boundary eigenvalue problem. In case of boundary conditions of a movable hinge support, exact formulas of eigenvalues and eigenfunctions were given. While in case of free edge pinching, a variational method was used in combination with a finite-difference method, and a computer program for solving the problem was built. It was established that one or two eigenfunctions expressing the deflection of the plate could correspond to the critical value of the compressive load parameter at which the stability of the compressed plate was lost. The results of numerical calculations of the critical values of the compressive load at different values of the orthotropy parameters were presented, and graphs of the corresponding equilibrium forms were constructed. For the case of a long orthotropic plate on an elastic base, it was established that the main term of the asymptotic expansion of the solution to the linear eigenvalue problem was determined from the problem of critical loads of a compressed beam on an elastic base with an elastic modulus that coincides with the elastic modulus of the plate in the longitudinal direction.
Discussion and Conclusions. The problem of critical loads of an orthotropic plate compressed in two directions lying on an elastic base was investigated. As the compressive load component increased along one direction, the critical value of the load compressing the plate along the other direction decreased. If an orthotropic plate was compressed by a load along a direction that corresponded to a greater bending stiffness, then the critical value of the loss of stability was greater than the critical value of the compressive load acting along the direction of a lesser bending stiffness. The presence of an elastic foundation increased the bearing capacity of the compressed plate.
Keywords
For citations:
Peshkhoev I.M., Sobol B.V. Critical Loads of Uniformly Compressed Orthotropic Rectangular Plate on an Elastic Base. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):214-223. https://doi.org/10.23947/2687-1653-2022-22-3-214-223
Introduction. L. M. Zubov in [1] derives the equilibrium equations of an elastic plate containing sources of internal stresses in the form of dislocations and disclinations, which are a modification of the Karman equations. In this work, the problem of bending a thin plate (membrane) under the action of internal stresses caused by defects is also solved. In [2–5], the theory of dislocations and disclinations is used in the study of the behavior of plates and shells. In article [6], a general solution of the oscillation equation of a rectangular orthotropic plate with free edges is constructed. In [7][8], asymptotic solutions of problems of statics and dynamics of narrow plates are constructed.
In [9], the problem of equilibria branching under the influence of a small normal pressure of a rectangular plate compressed in one direction with dislocations and disclinations is considered. The case is considered when the longitudinal edges of the plate are free from loads, and the other two edges are fixed. In [10], an asymptotic solution is provided for the problem of critical loads of a compressed narrow plate using a small parameter expansion of the relative width of the plate. In [11], the branching problem of the equilibria of an elastic rectangular plate with internal stress sources is investigated for the case when compressive loads are unevenly distributed along the edges. It is established that with even forms of the incompatibility function and even forms of distribution along the edges of compressive forces, the presence of a small normal load does not reduce the bearing capacity of the plate.
In work of Morozov N. F., Belyaev A. K., Tovstik P. E., Tovstik T. P. [12], an asymptotic derivation of two-dimensional equilibrium equations of a thin elastic inhomogeneous plate made of a general anisotropic material is presented. Conclusions about the forms of loss of stability of a compressed plate on an elastic soft base are formulated in [13]. In [14], the bending stiffness of a thin elastic multilayer plate with transversely isotropic layers is investigated. Two models of accounting for the effect of transverse shear are compared.
In [15], a model of thermoelastic viscoplastic deformation of a composite that is cross-reinforced with continuous fibers in arbitrary directions is constructed.
In [16], within the framework of a direct approach to plate theory, the problem of a hyperelastic plate with inhomogeneously distributed initial stresses is considered. The plate is considered as a material surface with five degrees of freedom (three displacements and two rotations). In [17], the stability of a uniformly compressed circular two-layer plate with an initially compressed or stretched layer is analyzed within the framework of nonlinear elasticity. A model of incompressible neo-Hookean material is used for determining the material ratio. The analysis of the dependence of the resulting critical stresses on the initial deformations and stiffness parameters is presented. In [18], the bending of a three-layer plate with surface and interfacial stresses is investigated, the theory of plates with first-order shear deformations and the Gurtin-Murdoch model of surface stresses are considered. The dependence of the plate stiffness parameters on the surface elasticity modules is analyzed. In [19], the problem of instability of a three-layer nonlinear elastic rectangular plate with a prestressed middle layer is considered.
In this paper, the influence of the parameters of the plate material and the elastic base parameter on the critical loads of the loss of stability of a compressed elastic rectangular orthotropic plate on an elastic base is investigated.
Materials and Methods. Let us consider an orthotropic rectangular plate lying on a linearly elastic base, which is compressed by forces P and Q along the X and Y axes. The equilibrium equations can be written as [7]:
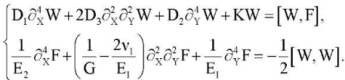 (1)
(1)
Let us write the boundary conditions in the form:
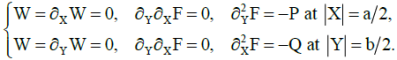 (2)
(2)
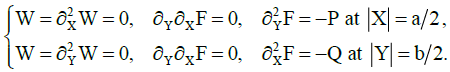 (3)
(3)
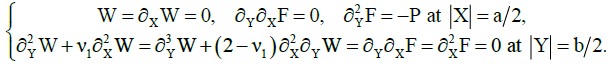 (4)
(4)
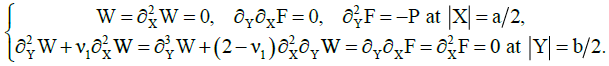 (5)
(5)
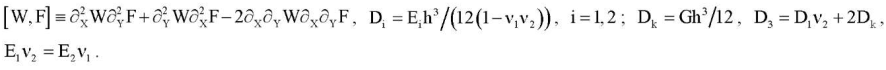
Here ν1, ν2, E1, E2, G — Poisson's coefficients, Young's modules for the main directions and the shear modulus of the plate material; D1, D2 — bending stiffness in the main directions; Dk — torsion stiffness; the function W(X,Y) denotes the stress function; h — plate thickness, KW — base reaction; K — modulus of subgrade reaction; the origin of coordinates X, Y s in the center of the plate and the axes are parallel to its edges; 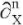 — partial derivative of the n-th order with respect to the variable X. We assume that the edges of the plate are loosely pinched (2) or pivotally supported (3). In this case, the compressive forces P and Q are evenly distributed along the edges X = ±a/2 and Y = ±b /2 respectively. The cases are also considered when two parallel edges of the plate Y = ±b /2 are free from loads, and the other two are freely pinched (4) or pivotally supported (5). In these cases, the compressive load is applied only to the edges X = ±a/2.
— partial derivative of the n-th order with respect to the variable X. We assume that the edges of the plate are loosely pinched (2) or pivotally supported (3). In this case, the compressive forces P and Q are evenly distributed along the edges X = ±a/2 and Y = ±b /2 respectively. The cases are also considered when two parallel edges of the plate Y = ±b /2 are free from loads, and the other two are freely pinched (4) or pivotally supported (5). In these cases, the compressive load is applied only to the edges X = ±a/2.
Let us assume that 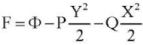 . Then, for the function Φ, homogeneous boundary conditions are valid ΦXY = ΦYY = 0 при |X| = a/2. ΦXY = ΦXX = 0 at |Y| = b/2. Let us move on to dimensionless variables by formulas:
. Then, for the function Φ, homogeneous boundary conditions are valid ΦXY = ΦYY = 0 при |X| = a/2. ΦXY = ΦXX = 0 at |Y| = b/2. Let us move on to dimensionless variables by formulas:
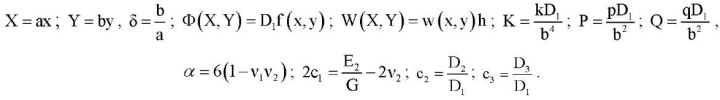
Then system of equations (1) and boundary conditions (2), (3) can be rewritten as
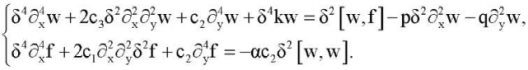 (6)
(6)
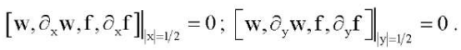 (7)
(7)
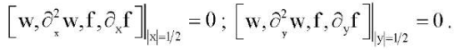 (8)
(8)
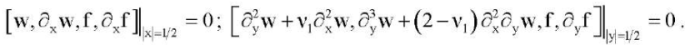 (9)
(9)
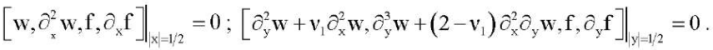 (10)
(10)
For any values of the parameters k, p, q the nonlinear boundary value problem (6) with any of the conditions (7)– (10) satisfies a trivial solution 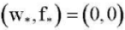 .
.
Let us denote by E2 the set of vector functions f = (f1, f2) with a finite norm, which is determined using the scalar product:
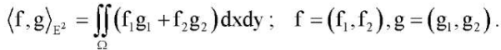 (11)
(11)
By E1 we denote the space of infinitely differentiable vector functions 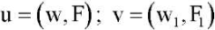 in the domain
in the domain 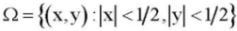 , which satisfy one of the boundary conditions (5) or (6) on the boundary
, which satisfy one of the boundary conditions (5) or (6) on the boundary  of the domain
of the domain  . We define the norm in E1 using the scalar product
. We define the norm in E1 using the scalar product
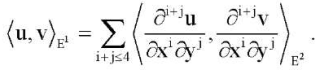 (12)
(12)
The boundary value problem (6) with one of the boundary conditions (7)–(10) can be considered as a nonlinear operator equation
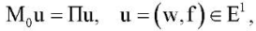 (13)
(13)
where
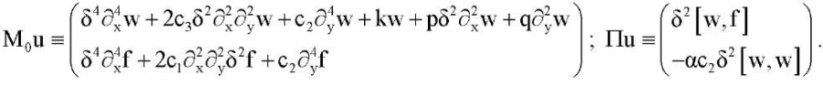 (14)
(14)
Here M0 — linear, and П — nonlinear operators, since
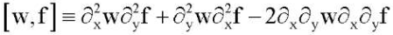
From the results of the works of I. I. Vorovich and N. F. Morozov, it follows [9] that the operators M0 and П act from the space E1 to E2. Let k = 0, p = 0, q = 0. Then equation (9) has a unique trivial solution 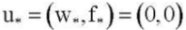 . With small changes in the values of the parameters p, q and k the trivial solution remains the only one. If, for any small values of a number ε > 0 and the fixed value k there are parameter values p, q, that satisfy the inequality
. With small changes in the values of the parameters p, q and k the trivial solution remains the only one. If, for any small values of a number ε > 0 and the fixed value k there are parameter values p, q, that satisfy the inequality 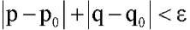 and for which there are at least two solutions to equation (9), then the point (p0, q0,) is called the branching point (or bifurcation point) [9] of this equation. It is shown in [9] that in order to find the bifurcation point (p0, q0), it is necessary to solve the eigenvalue boundary value problem, which is a linearized equation on a trivial solution
and for which there are at least two solutions to equation (9), then the point (p0, q0,) is called the branching point (or bifurcation point) [9] of this equation. It is shown in [9] that in order to find the bifurcation point (p0, q0), it is necessary to solve the eigenvalue boundary value problem, which is a linearized equation on a trivial solution
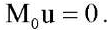 (15)
(15)
The eigenvalues (p0, q0) are the critical values of the parameters of the compressive load (p, q). Considering (13) and (14), equation (15) can be written as the following eigenvalue boundary value problem: to find values of the parameter p, such that for fixed values of the base parameter (modulus of subgrade reaction) k and the load parameter q along the y axis, the following problem has a nontrivial solution:
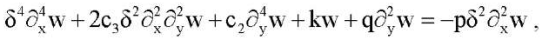 (16)
(16)
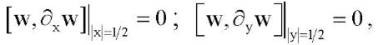 (17)
(17)
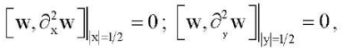 (18)
(18)
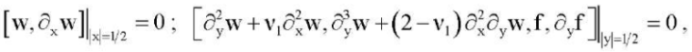 (19)
(19)
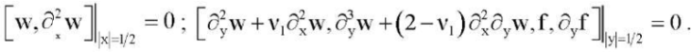 (20)
(20)
In this case, the critical value of the loss of stability of the compressed plate corresponds to the minimum eigenvalue of the parameter p, and the eigenfunction corresponding to this value shows the form of equilibrium after the loss of stability. For the case of the hinge support of the edges (18), exact solutions can be written for equation (16):
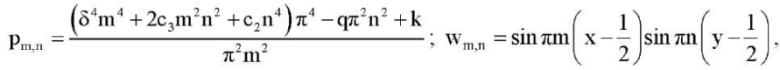 (21)
(21)
where m and n are arbitrary natural numbers.
From the analysis of formulas (21), it follows that with different ratios of the plate edge lengths δ, the physical parameters of the orthotropy of the plate material c3, c2, the parameter q of the compressive load along the y axis, and the modulus of subgrade reaction k (characterizing the reaction of the base), one or more half-waves in the form of equilibrium (21) can correspond to the critical load value 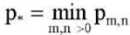 . In this case, the so-called buckling by two proper forms is possible, when, for example,
. In this case, the so-called buckling by two proper forms is possible, when, for example, 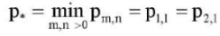 . Such cases are listed below. To solve the problem (16) with boundary conditions of free pinching of the edges (17), a variational method is used in combination with a finite-difference method, which was justified in [9][10] and is easily transferred to the case of an orthotropic plate. At the same time, the computer program developed for this task was tested on the solution of the problem (16), (18). In addition, a computer program has been developed for solving the variational method in combination with the finite difference method of the problem (16) with each of the boundary conditions (19), (20). For these cases, test examples of the corresponding boundary value problems have been constructed.
. Such cases are listed below. To solve the problem (16) with boundary conditions of free pinching of the edges (17), a variational method is used in combination with a finite-difference method, which was justified in [9][10] and is easily transferred to the case of an orthotropic plate. At the same time, the computer program developed for this task was tested on the solution of the problem (16), (18). In addition, a computer program has been developed for solving the variational method in combination with the finite difference method of the problem (16) with each of the boundary conditions (19), (20). For these cases, test examples of the corresponding boundary value problems have been constructed.
In [7], in the problem of asymptotic integration of the equation of small oscillations of a long (b << a) rectangular orthotropic plate, an expansion of the solution by small parameter degrees δ = b/a is constructed and it is shown that the main expansion is determined from the equation of vibrations of a beam with an elastic modulus E = E1. Repeating the reasoning of works [7] and [10], we will look for a solution to problem (16) with boundary conditions (19) or (20) in the form of series:
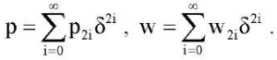 (22)
(22)
It can be shown that the main term of the asymptotic expansion (22) of the solution to problem (16) with boundary conditions (19) or (20) is determined from the problem in dimensionless variables about the critical loads of a compressed elastic beam on an elastic base with freely pinched or movably hinged edges:
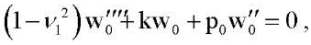 (23)
(23)
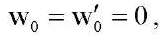 (24)
(24)
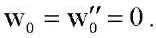 (25)
(25)
Here the prime symbol indicates the ordinary derivative of a function depending on the variable x. It is possible to construct an algorithm for determining all coefficients of the terms of the expansions (22), but the authors will not do this in this paper.
When moving to dimensional variables from (23)–(25), we obtain the problem of critical loads of a compressed beam with an elastic modulus E = E1. The eigenvalue problem (23) with boundary conditions (25) has an exact solution
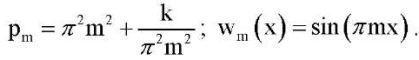 (26)
(26)
In the case of boundary conditions (24), problem (23) is solved by the variational-difference method.
Research Results. Numerical calculations of the critical values of the load parameter p compressing along the direction of the x axis with fixed values of the modulus of subgrade reaction k and fixed values of the load parameter q compressing along the direction of the y axis and the specified values of the orthotropy parameters of the plate material are carried out. The plate equilibrium forms corresponding to critical loads are constructed.
Example 1. Let us consider an example of a square orthotropic plate from work [16] "plywood of the first type" — three-ply: if you direct the x axis along the fibers of the face (upper and lower of the three layers), then Young's modules along the fibers and across, respectively, are equal to 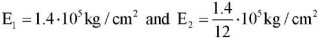 ; Poisson coefficients — ν1 = 0.46 and ν2 = 0.46 /12; shear modulus for the main directions of elasticity
; Poisson coefficients — ν1 = 0.46 and ν2 = 0.46 /12; shear modulus for the main directions of elasticity 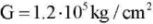 . Then, for the problem in dimensionless variables (16), we obtain
. Then, for the problem in dimensionless variables (16), we obtain 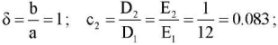
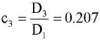 taking into account the above formulas for the transition to dimensionless variables. Let the edges of the plate be pivotally supported. Then, from (21) for k = 0, q = 8.193, it follows
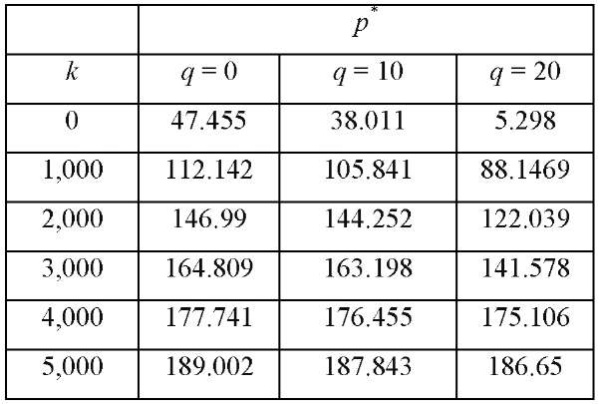
taking into account the above formulas for the transition to dimensionless variables. Let the edges of the plate be pivotally supported. Then, from (21) for k = 0, q = 8.193, it follows 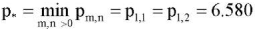 . Two forms of equilibrium correspond to this critical value. Table 1 shows the values of the critical load p* loss of stability of an orthotropic plate with pinched edges compressed along the x axis for different values of the modulus of subgrade reaction k and different values of the compressive load along the y axis. Table 1 shows that with an increase in the value of the modulus of subgrade reaction, the critical load of the loss of stability of the compressed orthotropic plate also increases.
. Two forms of equilibrium correspond to this critical value. Table 1 shows the values of the critical load p* loss of stability of an orthotropic plate with pinched edges compressed along the x axis for different values of the modulus of subgrade reaction k and different values of the compressive load along the y axis. Table 1 shows that with an increase in the value of the modulus of subgrade reaction, the critical load of the loss of stability of the compressed orthotropic plate also increases.
Table 1
Dependence of the critical load p* on the base parameter k at different q
Example 2. Let us consider the same orthotropic plate from Example 1 and direct the x axis across the fibers of the face. Then Young's modules along the x and y axes are 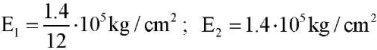 respectively; Poisson's coefficients — ν1 = 0.46 /12 and ν2 = 0.46; shear modulus for the main directions of elasticity
respectively; Poisson's coefficients — ν1 = 0.46 /12 and ν2 = 0.46; shear modulus for the main directions of elasticity 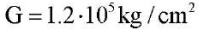 . Then, for the problem in dimensionless variables (12), we obtain
. Then, for the problem in dimensionless variables (12), we obtain 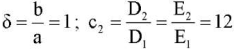 ;
;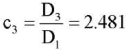 . Let the boundary conditions (13) be fulfilled — the edges of the plate are freely pinched. As a result of numerical calculations using a computer program for solving the problem (12), (13) for this orthotropic plate, dependencies are constructed between the load q on the y axis and the critical value p* of the load p on the x axis at fixed values of the remaining parameters of this problem. Table 2 shows the values (q, p*) at k = 0.
. Let the boundary conditions (13) be fulfilled — the edges of the plate are freely pinched. As a result of numerical calculations using a computer program for solving the problem (12), (13) for this orthotropic plate, dependencies are constructed between the load q on the y axis and the critical value p* of the load p on the x axis at fixed values of the remaining parameters of this problem. Table 2 shows the values (q, p*) at k = 0.
Table 2
Dependence between q and p* at k = 0

It should be noted that all six points (q, p*) correspond to the form of equilibrium, gradually transforming from the form shown in Fig. 1 a to the form in Fig. 1 c. Figure 1 illustrates the first, third and sixth eigenfunctions corresponding to the critical points (q, p*) of Table 1. These eigenfunctions show the forms of equilibrium of the plate after loss of stability (forms of loss of stability).
Fig. 1. Forms of plate stability loss:
а — at q = 0, p = 254.388;
b — at q = 200, p = 227.789;
c — at q = 400, p = 166.462
As a result of numerical calculations using a computer program for solving the boundary value problem (16), (17) for this orthotropic plate, parameter values are found k = 200, q = 0 for which two eigenfunctions w1 and w2 correspond to the eigenvalue p* = 255.6. This case corresponds to the loss of stability of the plate in two proper forms. Figure 2 shows graphs of the forms of stability loss corresponding to this case.
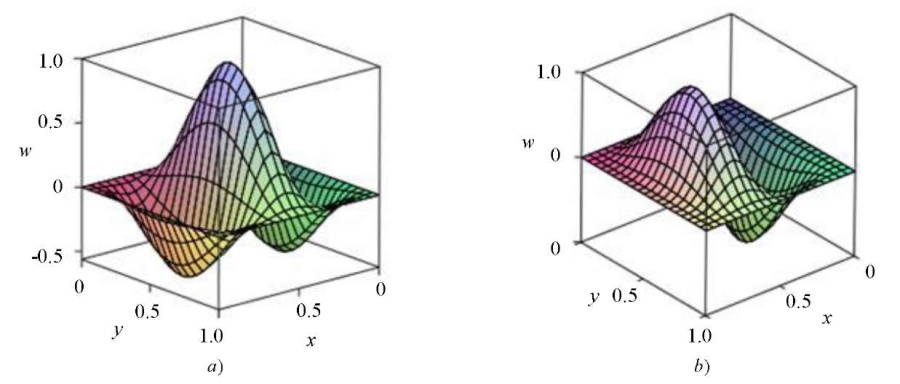
Fig. 2. Two forms of stability loss: а — w1; б — w2
Example 3. Let us consider an orthotropic plate with parameters 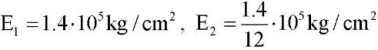 ; Poisson coefficients — ν1 = 0.46 и ν2 = 0.46 /12; shear modulus for the main directions of elasticity
; Poisson coefficients — ν1 = 0.46 и ν2 = 0.46 /12; shear modulus for the main directions of elasticity 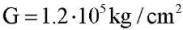 . Let the length of the plate be a = 5, the width — b = 1, the edges
. Let the length of the plate be a = 5, the width — b = 1, the edges 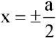 — are pinched, and the edges
— are pinched, and the edges 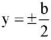 are free, the parameter —
are free, the parameter — 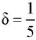 (the plate can be considered long), modulus of subgrade reaction — k = 350. Numerical calculation of the solution of the problem (16) with boundary conditions (17) gives the value of the critical load p = 37.42, the graph of the corresponding eigenfunction is shown in Fig. 3a. Numerical calculation of the solution to the problem (23), (24) at ν1 = 0.46 and k = 350 for a beam of length a = 5 gives p0 = 39.01, while the eigenfunction has the form shown in Fig. 3b. As you can see, the critical load of the plate stability loss coincides with the critical load of the beam with an error
(the plate can be considered long), modulus of subgrade reaction — k = 350. Numerical calculation of the solution of the problem (16) with boundary conditions (17) gives the value of the critical load p = 37.42, the graph of the corresponding eigenfunction is shown in Fig. 3a. Numerical calculation of the solution to the problem (23), (24) at ν1 = 0.46 and k = 350 for a beam of length a = 5 gives p0 = 39.01, while the eigenfunction has the form shown in Fig. 3b. As you can see, the critical load of the plate stability loss coincides with the critical load of the beam with an error 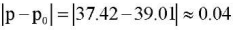 . The eigenfunctions of problems (16), (17) and (23), (24) have the same number of half-waves.
. The eigenfunctions of problems (16), (17) and (23), (24) have the same number of half-waves.
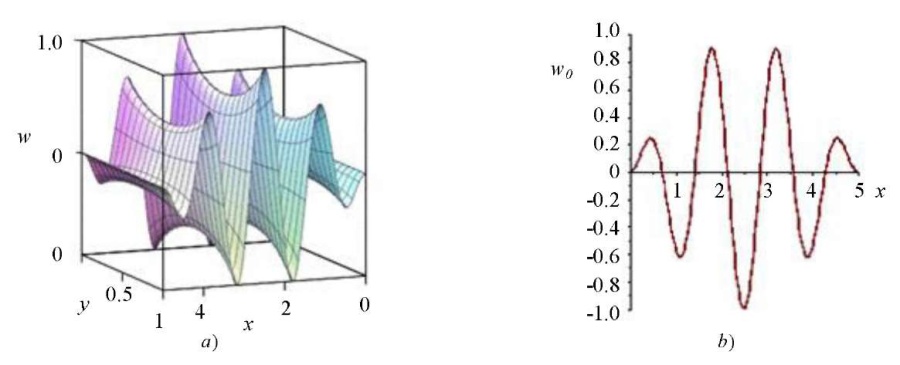
Fig. 3. Forms of stability loss: а — w(x,y), compressed orthotropic long plate; b — w0(x), compressed beam
Discussion and Conclusion. The problem of critical loads of an orthotropic plate compressed in two directions lying on an elastic base is investigated. The problem is reduced to solving a parametric linear boundary value eigenvalue problem. In the case of boundary conditions of a movable hinge support, exact formulas of eigenvalues and eigenfunctions are given, and in the case of free pinching of the edges, a variational method is applied in combination with a finite difference method and a computer program for solving the problem is constructed. The following conclusions are obtained:
- When the compressive load component q increases along the y axis, the critical value p* of the load compressing the plate along the x axis decreases.
- If an orthotropic plate is compressed by a load along a direction that corresponds to greater bending stiffness, then the critical value of the loss of stability is greater than the critical value of the compressive load acting along the direction of lesser bending stiffness.
- In the presence of an elastic base, a greater value of the modulus of subgrade reaction k > 0 corresponds to a greater value of the critical value of the compressive load. The presence of an elastic base increases the bearing capacity of the compressed plate.
- In the case of a long orthotropic plate on an elastic base, the critical load of a compressed plate can be calculated approximately as the critical load of a compressed beam on an elastic base with an elastic modulus equal to the elastic modulus of the plate in the longitudinal direction.
References
1. Зубов, Л. М. Уравнения Кармана для упругой пластинки с дислокациями и дисклинациями / Л. М. Зубов // Доклады академии наук. — 2007. — Т. 412. — С. 343–346.
2. Zubov, L. M. The Linear Theory of Dislocation and Disclinations in Elastic Shells / L. M. Zubov // Journal of Applied Mathematics and Mechanics. — 2010. — Vol. 74. — P. 663–672. https://doi.org/10.1016/j.jappmathmech.2011.01.006
3. Зубов, Л. М. Теория дислокаций и дисклинаций в упругих пластинках / Л. М. Зубов, А. В. Столповский // Прикладная математика и механика. — 2008. — Т. 72. — C. 996–1013.
4. Зубов, Л. М. Сильный изгиб круглой пластинки с непрерывно распределенными дисклинациями / Л. М. Зубов, Фам Тан Хунг // Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. — 2010. — № 4 (158). — С. 28–33.
5. Зубов, Л. М. Осесимметричнный изгиб нелинейно упругой кольцевой пластики с распределенными дисклинациями / Л. М. Зубов, Т. Х. Фам // Экологический вестник научных центров ЧЭС. — 2010. — № 4. — C. 36–43.
6. Папков, С. О. Колебания прямоугольной ортотропной пластины со свободными краями: анализ и решение бесконечной системы / С. О. Папков // Акустический журнал. — 2015. — Т. 61. — С. 152–160. https://doi.org/10.7868/S0320791915010086
7. Столяр, А. М. Поведение узких панелей и сферических оболочек в условиях статического и динамического нагружения. Асимптотический и численный анализ: монография / А. М. Столяр. — Ростов-на-Дону : Издательство Южного федерального университета, 2014. — 146 с.
8. Finiukova, V. O. Asymptotic Integration of One Narrow Plate Problem / V. O. Finiukova, A. M. Stolyar // In book: Shell-like Structures. Non-Classical Theories and Applications. Advanced Structured Materials Series. — 2011. — Vol. 15. — P. 53–62. Springer-Verlag: Berlin – Heidelberg.
9. Пешхоев, И. М. Выпучивание сжатой упругой прямоугольной пластины со свободными краями / И. М. Пешхоев, Б. В. Соболь // Проблемы прочности и пластичности. — 2020. — Т. 82. — С. 244–251. https://doi.org/10.32326/1814-9146-2020-82-2-244-251
10. Пешхоев, И. М. Асимптотика критических нагрузок сжатой узкой упругой пластины с внутренними напряжениями / И. М. Пешхоев // Проблемы прочности и пластичности. — 2021. — Т. 82. — С. 227–234. https://doi.org/10.32326/1814-9146-2021-83-2-227-234
11. Peshkhoev, I. M. Buckling of the Nonuniformly Compressed Plate with Dislocations and Disclinations / I. M. Peshkhoev, A. M. Stolyar // In book: Analysis of Shells, Plates, and Beams. Advanced Structured Materials Series. — 2020. — Vol. 134. — P. 345–366. Springer, Cham. http://dx.doi.org/10.1007/978-3-030-47491-1_18
12. Two-dimensional linear models of multilayered anisotropic plates / A. K. Belyaev, N. F. Morozov, P. E. Tovstik, T. P. Tovstik // Acta Mechanica. — 2019. — Vol. 230. — P. 2891–2904. https://doi.org/10.1007/s00707-019-02405-y
13. Морозов, Н. Ф. О формах потери устойчивости сжатой пластины на упругом основании / Н. Ф. Морозов, П. Е. Товстик // Доклады академии наук. — 2012. — Т. 446. — С. 37–41.
14. Морозов, Н. Ф. Изгибная жесткость многослойных пластин / Н. Ф. Морозов, П. Е. Товстик, Т. П. Товстик // Известия Российской академии наук. Механика твердого тела. — 2020. — № 5. — С. 7–12. https://doi.org/10.31857/S0572329920050128
15. Янковский, А. П. Моделирование термоупруговязкопластического деформирования гибких армированных пластин / А. П. Янковский // Прикладная математика и механика. — 2022. — Т. 86. — С. 121–150. https://doi.org/10.31857/S003282352201009X
16. Altenbach, H. On the Effective Stiffness of Plates Made of Hyperelastic Materials with Initial Stresses / H. Altenbach, V. A. Eremeyev // International Journal of Non-Linear Mechanics. — 2010. — Vol. 45. — P. 976–981. https://doi.org/10.1016/j.ijnonlinmec.2010.04.007
17. Eremeev, V. V. Buckling of a Two-Layered Circular Plate with a Prestressed Layer / V. V. Eremeev, L. M. Zubov // Mathematics and Mechanics of Solids. — 2017. — Vol. 22. — P. 773–781. https://doi.org/10.1177/1081286515612527
18. Altenbach, H. Bending of a Three-Layered Plate with Surface Stresses / H. Altenbach, V. A. Eremeyev // In book: Analysis and Modelling of Advanced Structures and Smart Systems. Advanced Structured Materials Series. — 2018. — Vol. 81. — P. 1–10. Springer: Singapore. https://doi.org/10.1007/978 – 981-10 – 6895-9_1
19. Eremeev, V. V. On Instability of Three-Layered Nonlinear Elastic Rectangular Plate with Prestressed Middle Layer / V. V. Eremeev, L. M. Zubov // In book: Shell Structures: Theory and Applications. — 2018. — Vol. 4. — P. 215–218. London: CRC Press, Taylor and Francis Group.
About the Authors
I. M. PeshkhoevRussian Federation
1, Gagarin sq., Rostov-on-Don
B. V. Sobol
Russian Federation
1, Gagarin sq., Rostov-on-Don
Review
For citations:
Peshkhoev I.M., Sobol B.V. Critical Loads of Uniformly Compressed Orthotropic Rectangular Plate on an Elastic Base. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):214-223. https://doi.org/10.23947/2687-1653-2022-22-3-214-223
JATS XML














































