Перейти к:
Критические нагрузки равномерно сжатой ортотропной прямоугольной пластины на упругом основании
https://doi.org/10.23947/2687-1653-2022-22-3-214-223
Аннотация
Введение. Рассматривается задача о критических нагрузках сжатой ортотропной прямоугольной пластины на упругом основании. Для пластины заданы параметры ортотропии: коэффициенты Пуассона, модули Юнга для главных направлений и модуль сдвига материала пластины. Составляющие сжимающей нагрузки равномерно распределены по двум противоположным краям пластины и действуют параллельно осям координат. Края пластины свободно защемлены или шарнирно оперты. Рассмотрены также случаи, когда два параллельных края пластины свободны от нагрузок, а два других свободно защемлены или шарнирно оперты.
Материалы и методы. Задача рассматривается на основе системы нелинейных уравнений равновесия типа Кармана. Критические значения параметра нагрузки определяются из линеаризованной на тривиальном решении задачи. При этом для решения краевой задачи на собственные значения применяется вариационный метод в сочетании с конечно-разностным методом.
Результаты исследования. Задача сведена к решению параметрической линейной краевой задачи на собственные значения. В случае краевых условий подвижного шарнирного опирания приведены точные формулы собственных значений и собственных функций, а в случае свободного защемления краев применен вариационный метод в сочетании с конечно-разностным методом и построена компьютерная программа решения задачи. Установлено, что критическому значению параметра сжимающей нагрузки, при котором происходит потеря устойчивости сжатой пластины, может соответствовать одна или две собственные функции, выражающие прогиб пластины. Приведены результаты численных расчетов критических значений сжимающей нагрузки при различных значениях параметров ортотропии и построены графики соответствующих форм равновесия. Для случая длинной ортотропной пластины на упругом основании установлено, что главный член асимптотического разложения решения линейной задачи на собственные значения определяется из задачи о критических нагрузках сжатой балки на упругом основании с модулем упругости, совпадающим с модулем упругости пластины по продольному направлению.
Обсуждение и заключения. Исследована задача о критических нагрузках сжатой в двух направлениях ортотропной пластины, лежащей на упругом основании. При повышении составляющей сжимающей нагрузки вдоль одного направления снижается величина критического значения нагрузки, сжимающей пластину вдоль другого направления. Если ортотропная пластина сжимается нагрузкой вдоль направления, которое соответствует большей изгибной жесткости, то критическое значение потери устойчивости больше, чем критическое значение действующей вдоль направления меньшей изгибной жесткости сжимающей нагрузки. Наличие упругого основания повышает несущую способность сжатой пластины.
Ключевые слова
Для цитирования:
Пешхоев И.М., Соболь Б.В. Критические нагрузки равномерно сжатой ортотропной прямоугольной пластины на упругом основании. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):214-223. https://doi.org/10.23947/2687-1653-2022-22-3-214-223
For citation:
Peshkhoev I.M., Sobol B.V. Critical Loads of Uniformly Compressed Orthotropic Rectangular Plate on an Elastic Base. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):214-223. https://doi.org/10.23947/2687-1653-2022-22-3-214-223
Введение. Л. М. Зубов в работе [1] вывел уравнения равновесия упругой пластинки, содержащей источники внутренних напряжений в виде дислокаций и дисклинаций, являющиеся модификацией уравнений Кармана. В этой работе также решена задача об изгибе тонкой пластинки (мембраны) под действием внутренних напряжений, обусловленных дефектами. В работах [2–5] теория дислокаций и дисклинаций применяется в исследовании поведения пластин и оболочек. В статье [6] построено общее решение уравнения колебаний прямоугольной ортотропной пластины со свободными краями. В работах [7][8] строятся асимптотические решения задач статики и динамики узких пластин.
В работе [9] рассмотрена задача о ветвлении равновесий под влиянием малого нормального давления сжатой в одном направлении прямоугольной пластины, содержащей дислокации и дисклинации. Рассмотрен случай, когда продольные края пластины свободны от нагрузок, а два других края закреплены. В [10] для задачи о критических нагрузках сжатой узкой пластины строится асимптотическое решение с помощью разложения по малому параметру относительной ширины пластины. В [11] исследована задача о ветвлении равновесий упругой прямоугольной пластины с внутренними источниками напряжений для случая, когда сжимающие нагрузки неравномерно распределены по краям. Установлено, что при четных формах функции несовместности и четных формах распределения по краям сжимающих усилий наличие малой нормальной нагрузки не снижает несущую способность пластины.
В работе Морозова Н. Ф., Беляева А. К., Товстика П. Е., Товстик Т. П. [12] представлен асимптотический вывод двумерных уравнений равновесия тонкой упругой неоднородной пластины, изготовленной из анизотропного материала общего вида. В [13] сформулированы выводы о формах потери устойчивости сжатой пластины на упругом мягком основании. В работе [14] исследована жесткость на изгиб тонкой упругой многослойной пластины с трансверсально изотропными слоями. Проводится сравнение двух моделей учета влияния поперечного сдвига.
В работе [15] построена модель термоупруговязкопластической деформации композита, который перекрестно армирован непрерывными волокнами в произвольных направлениях.
В [16] в рамках прямого подхода к теории пластин рассматривается задача о гиперупругой пластине с неоднородно распределенными начальными напряжениями. Пластина рассматривается как материальная поверхность с пятью степенями свободы (три перемещения и два вращения). В работе [17] в рамках нелинейной упругости анализируется устойчивость равномерно сжатой круглой двухслойной пластины с первоначально сжатым или растянутым слоем. Для определяющего соотношения материала используется модель несжимаемого неогуковского материала. Представлен анализ зависимости результирующих критических напряжений от начальных деформаций и параметров жесткости. В работе [18] исследуется изгиб трехслойной пластины, содержащей поверхностные и межфазные напряжения, рассмотрена теория пластин с деформациями сдвига первого порядка и модель поверхностных напряжений Гуртина-Мердока. Анализируется зависимость параметров жесткости пластины от модулей поверхностной упругости. В работе [19] рассматривается задача о неустойчивости трехслойной нелинейно-упругой прямоугольной пластины с предварительно напряженным средним слоем.
В настоящей работе исследуется влияние параметров материала пластины и параметра упругого основания на критические нагрузки потери устойчивости сжатой упругой прямоугольной ортотропной пластины на упругом основании.
Материалы и методы. Рассмотрим лежащую на линейно упругом основании ортотропную прямоугольную пластину, которая сжимается усилиями P и Q вдоль осей X и Y. Уравнения равновесия можно записать в виде [7]:
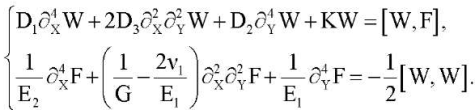 (1)
(1)
Краевые условия запишем в виде:
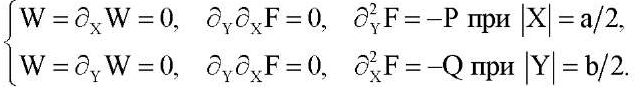 (2)
(2)
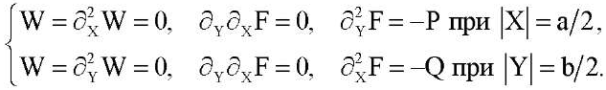 (3)
(3)
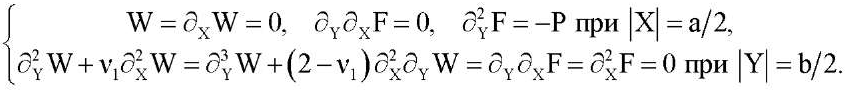 (4)
(4)
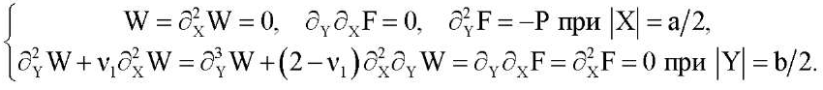 (5)
(5)
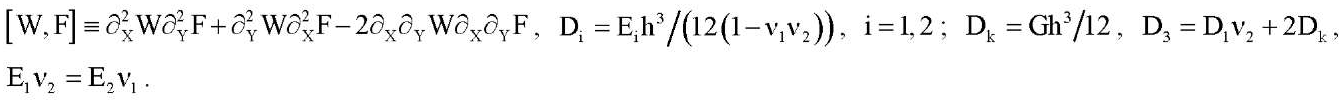
Здесь ν1, ν2, E1, E2, G — коэффициенты Пуассона, модули Юнга для главных направлений и модуль сдвига материала пластины; D1, D2 — жесткости изгиба по главным направлениям; Dk — жесткость кручения; функция W(X,Y) выражает прогиб, а F(X,Y) обозначает функцию напряжений; h — толщина пластины; KW — реакция основания; K — коэффициент постели; начало координат X, Y располагается в центре пластины и оси параллельны ее краям; 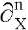 — частная производная n-го порядка по переменной X. Мы полагаем, что края пластины свободно защемлены (2) или шарнирно оперты (3). При этом сжимающие усилия P и Q равномерно распределены по краям X = ±a/2 и Y = ±b /2 соответственно. Рассматриваются также случаи, когда два параллельных края пластины Y = ±b /2 свободны от нагрузок, а два других свободно защемлены (4) или шарнирно оперты (5). В этих случаях сжимающая нагрузка приложена только к краям X = ±a/2.
— частная производная n-го порядка по переменной X. Мы полагаем, что края пластины свободно защемлены (2) или шарнирно оперты (3). При этом сжимающие усилия P и Q равномерно распределены по краям X = ±a/2 и Y = ±b /2 соответственно. Рассматриваются также случаи, когда два параллельных края пластины Y = ±b /2 свободны от нагрузок, а два других свободно защемлены (4) или шарнирно оперты (5). В этих случаях сжимающая нагрузка приложена только к краям X = ±a/2.
Положим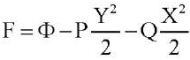 . Тогда для функции Φ справедливы однородные краевые условия ΦXY = ΦYY = 0 при |X| = a/2. ΦXY = ΦXX = 0 при |Y| = b/2. Эти условия можно заменить на эквивалентные краевые условия Φ = ΦX = 0 при |X| = a/2. Φ = ΦY = 0 при |Y| = b/2. Перейдем к безразмерным переменным по формулам:
. Тогда для функции Φ справедливы однородные краевые условия ΦXY = ΦYY = 0 при |X| = a/2. ΦXY = ΦXX = 0 при |Y| = b/2. Эти условия можно заменить на эквивалентные краевые условия Φ = ΦX = 0 при |X| = a/2. Φ = ΦY = 0 при |Y| = b/2. Перейдем к безразмерным переменным по формулам:
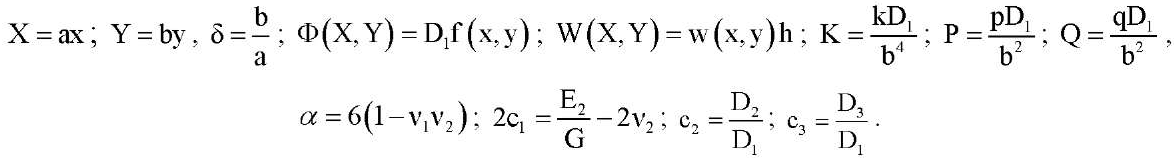
Тогда систему уравнений (1) и краевые условия (2), (3) можно переписать в виде:
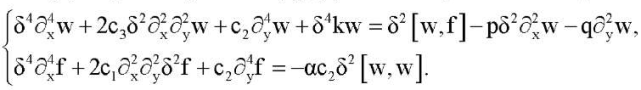 (6)
(6)
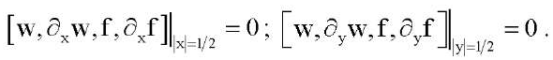 (7)
(7)
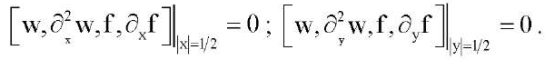 (8)
(8)
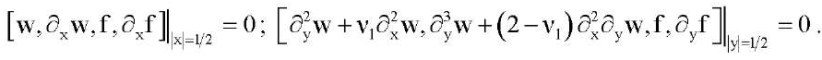 (9)
(9)
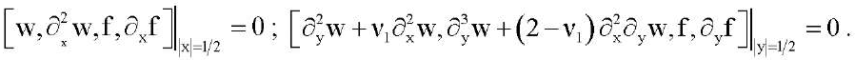 (10)
(10)
При любых значениях параметров k, p, q нелинейной краевой задаче (6) с любым из условий (7)–(10) удовлетворяет тривиальное решение 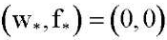
Обозначим через E2 множество вектор-функций f = (f1, f2) с конечной нормой, которая определяется с помощью скалярного произведения:
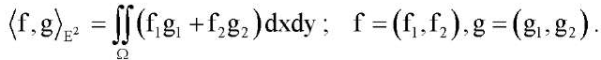 (11)
(11)
Через E1 обозначим пространство бесконечно дифференцируемых в области 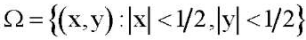 вектор-функций
вектор-функций 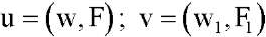 , которые удовлетворяют на границе
, которые удовлетворяют на границе  области
области  одному из краевых условий (5) или (6). Норму в E1 определим с помощью скалярного произведения:
одному из краевых условий (5) или (6). Норму в E1 определим с помощью скалярного произведения:
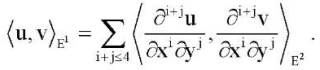 (12)
(12)
Краевая задача (6) с одним из краевых условий (7)–(10) может быть рассмотрена как нелинейное операторное уравнение:
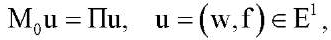 (13)
(13)
где
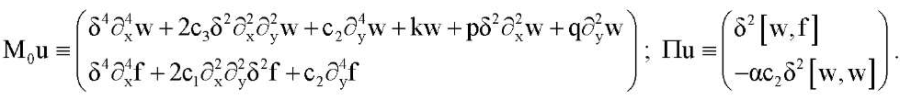 (14)
(14)
Здесь M0 — линейный, а П — нелинейный операторы, так как:
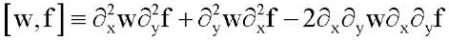
Из результатов работ И. И. Воровича и Н. Ф. Морозова следует [9], что операторы M0 и П действуют из пространства E1 в E2. Пусть k = 0, p = 0, q = 0. Тогда уравнение (9) имеет единственное тривиальное решение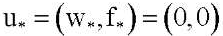 . При малых изменениях величин параметров p, q и k тривиальное решение остается единственным. Если при любых малых значениях числа ε > 0 и фиксированном значении k существуют значения параметров p, q, которые удовлетворяют неравенству
. При малых изменениях величин параметров p, q и k тривиальное решение остается единственным. Если при любых малых значениях числа ε > 0 и фиксированном значении k существуют значения параметров p, q, которые удовлетворяют неравенству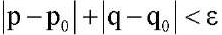 и для которых существуют хотя бы два решения уравнения (9), то точку (p0, q0,) называют точкой ветвления (или точкой бифуркации) [9] этого уравнения. В работе [9] показано, что для нахождения точки бифуркации (p0, q0) надо решить краевую задачу на собственные значения, которая представляет собой линеаризованное на тривиальном решении уравнение:
и для которых существуют хотя бы два решения уравнения (9), то точку (p0, q0,) называют точкой ветвления (или точкой бифуркации) [9] этого уравнения. В работе [9] показано, что для нахождения точки бифуркации (p0, q0) надо решить краевую задачу на собственные значения, которая представляет собой линеаризованное на тривиальном решении уравнение:
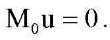 (15)
(15)
Собственные значения (p0, q0,) являются критическими значениями параметров сжимающей нагрузки (p, q). Учитывая (13) и (14), уравнение (15) можно записать как следующую краевую задачу на собственные значения: найти такие значения параметра p, что для фиксированных значений параметра основания (коэффициента постели) k и параметра q нагрузки вдоль оси y, следующая задача имеет нетривиальное решение:
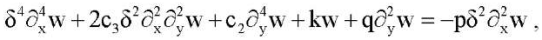 (16)
(16)
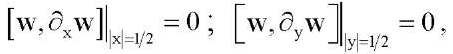 (17)
(17)
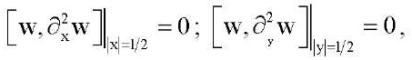 (18)
(18)
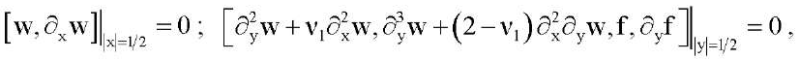 (19)
(19)
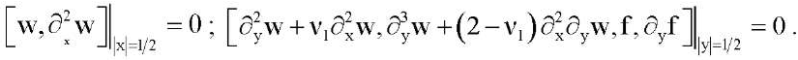 (20)
(20)
При этом критическому значению потери устойчивости сжатой пластины отвечает минимальное собственное значение параметра p, а соответствующая этому значению собственная функция показывает форму равновесия после потери устойчивости. Для случая шарнирного опирания краев (18) для уравнения (16) можно записать точные решения:
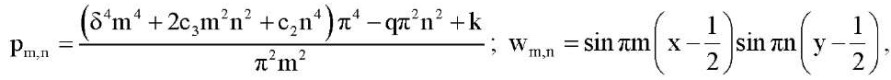 (21)
(21)
где m и n произвольные натуральные числа.
Из анализа формул (21) следует, что при различных отношениях длин краев пластины δ, физических параметров ортотропности материала пластины c3, c2, параметра q сжимающей нагрузки по оси y, и коэффициента постели k (характеризующего реакцию основания) критическому значению нагрузки 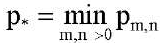 может соответствовать одна или несколько полуволн в форме равновесия (21). При этом возможно так называемое выпучивание по двум собственным формам, когда, например,
может соответствовать одна или несколько полуволн в форме равновесия (21). При этом возможно так называемое выпучивание по двум собственным формам, когда, например, 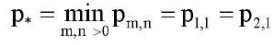 . Ниже приводятся такие случаи. Для решения задачи (16) с краевыми условиями свободного защемления краев (17) применяется вариационный метод в сочетании с конечно-разностным методом, который был обоснован в работах [9][10] и легко переносится на случай ортотропной пластины. При этом разработанная для этой задачи компьютерная программа тестировалась на решении задачи (16), (18).
. Ниже приводятся такие случаи. Для решения задачи (16) с краевыми условиями свободного защемления краев (17) применяется вариационный метод в сочетании с конечно-разностным методом, который был обоснован в работах [9][10] и легко переносится на случай ортотропной пластины. При этом разработанная для этой задачи компьютерная программа тестировалась на решении задачи (16), (18).
Кроме этого, разработана компьютерная программа решения вариационным методом в сочетании с конечно- разностным методом задачи (16) с каждым из краевых условий (19), (20). Для этих случаев были сконструированы тестовые примеры соответствующих краевых задач.
В работе [7] в задаче об асимптотическом интегрировании уравнения малых колебаний длинной (b << a) прямоугольной ортотропной пластины построено разложение решения по степеням малого параметра δ = b/a и показано, что главный член разложения определяется из уравнения колебаний балки с модулем упругости E = E1. Повторяя рассуждения работ [7] и [10] будем искать решение задачи (16) с краевыми условиями (19) или (20) в виде рядов:
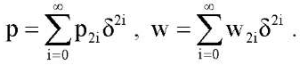 (22)
(22)
Можно показать, что главный член асимптотического разложения (22) решения задачи (16) с краевыми условиями (19) или (20) определяется из задачи в безразмерных переменных о критических нагрузках сжатой упругой балки на упругом основании со свободно защемленными или подвижно шарнирно опертыми краями:
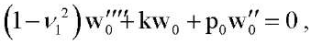 (23)
(23)
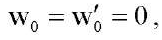 (24)
(24)
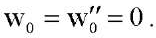 (25)
(25)
Здесь штрихом обозначена обыкновенная производная функции, зависящей от переменной x. Можно построить алгоритм определения всех коэффициентов слагаемых разложений (22), но авторы не будут этого делать в данной работе.
При переходе к размерным переменным из (23)–(25) получаем задачу о критических нагрузках сжатой балки с модулем упругости E = E1. Задача на собственные значения (23) с краевыми условиями (25) имеет точное решение:
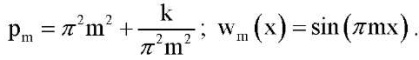 (26)
(26)
В случае краевых условий (24) задача (23) решается вариационно-разностным методом.
Результаты исследования. Проведены численные расчеты критических значений параметра нагрузки p, сжимающей вдоль направления оси x при фиксированных значениях коэффициента постели k, и фиксированных значениях параметра нагрузки q, сжимающей вдоль направления оси y и заданных значениях параметров ортотропии материала пластины. Построены соответствующие критическим нагрузкам формы равновесия пластины.
Пример 1. Рассмотрим пример квадратной ортотропной пластины из работы [16] «фанера первого типа» — трехслойная фанера: если направить ось x вдоль волокон рубашки (верхнего и нижнего из трех слоёв), то модули Юнга вдоль волокон и поперек соответственно равны  ; коэффициенты Пуассона — ν1 = 0,46 и ν2 = 0,46 /12; модуль сдвига для главных направлений упругости
; коэффициенты Пуассона — ν1 = 0,46 и ν2 = 0,46 /12; модуль сдвига для главных направлений упругости 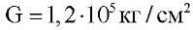 . Тогда для задачи в безразмерных переменных (16) получим
. Тогда для задачи в безразмерных переменных (16) получим 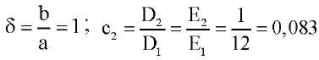 ;
; 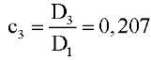
учитывая приведенные выше формулы перехода к безразмерным переменным. Пусть края пластины шарнирно оперты. Тогда из (21) при k = 0, q = 8,193 следует
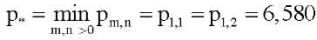
Этому критическому значению отвечают две формы равновесия
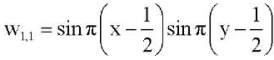
и
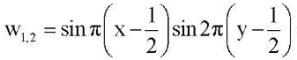
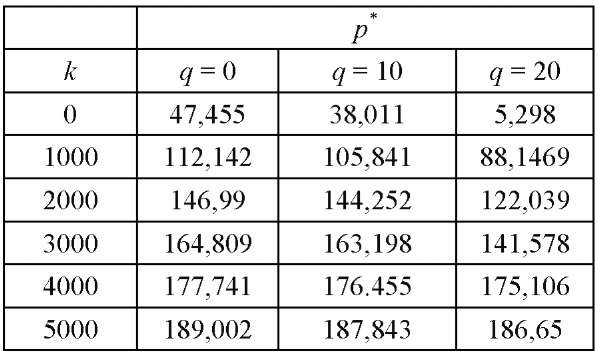
В таблице 1 приведены значения критической нагрузки p* потери устойчивости ортотропной пластины с защемленными краями, сжатой по оси x, для различных значений коэффициента постели k и различных значениях сжимающей нагрузки по оси y. Таблица 1 показывает, что при повышении значения коэффициента постели критическая нагрузка потери устойчивости сжатой ортотропной пластины также повышается.
Таблица 1
Зависимость критической нагрузки p* от параметра основания k при различных q
Пример 2. Рассмотрим ту же ортотропную пластину из примера 1 и направим ось x поперек волокон рубашки. Тогда модули Юнга вдоль осей x и y соответственно равны
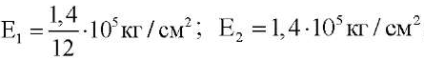 ;
;
коэффициенты Пуассона — ν1 = 0,46 /12 и ν2 = 0,46; модуль сдвига для главных направлений упругости 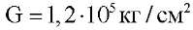 . Тогда для задачи в безразмерных переменных (12) получим
. Тогда для задачи в безразмерных переменных (12) получим
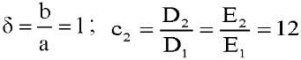 ;
; 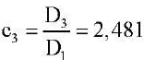
Пусть выполняются краевые условия (13) — края пластины свободно защемлены. В результате численных расчетов с помощью компьютерной программы решения задачи (12), (13) для данной ортотропной пластины построены зависимости между нагрузкой q по оси y и критическим значением p* нагрузки p по оси x при фиксированных значениях остальных параметров этой задачи. В таблице 2 приведены значения (q, p*) при k = 0.
Таблица 2
Зависимость между q и p* при k = 0

Отметим, что всем шести точкам (q, p*) отвечает форма равновесия, постепенно трансформирующаяся от вида, представленного на рис. 1 а, до вида на рис. 1 в. На рис. 1 проиллюстрированы первая, третья и шестая собственные функции, соответствующие критическим точкам (q, p*) таблицы 1. Эти собственные функции показывают формы равновесия пластины после потери устойчивости (формы потери устойчивости).
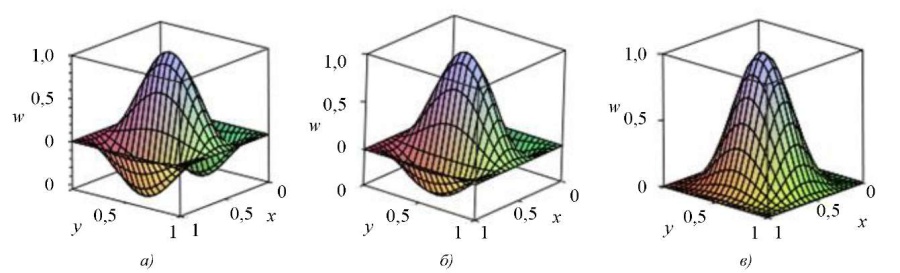
Рис. 1. Формы потери устойчивости пластины:
а — при q = 0, p = 254,388;
б — при q = 200, p = 227,789;
в — при q = 400, p = 166,462
В результате численных расчетов с помощью компьютерной программы решения краевой задачи (16), (17) для данной ортотропной пластины найдены значения параметров k = 200, q = 0 при которых собственному значению p* = 255,6 отвечают две собственные функции w1 и w2. Этот случай соответствует потере устойчивости пластины по двум собственным формам. На рис. 2 представлены графики соответствующих этому случаю форм потери устойчивости.
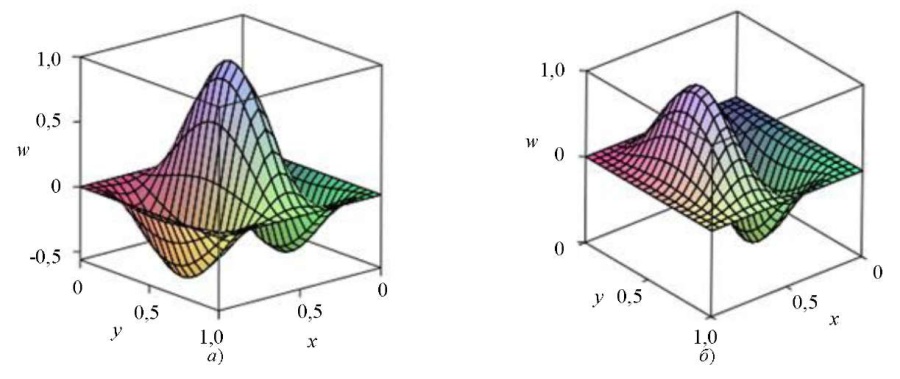
Рис. 2. Две формы потери устойчивости: а — w1; б — w2
Пример 3. Рассмотрим ортотропную пластину с параметрами 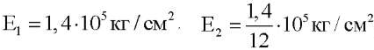
коэффициенты Пуассона — ν1 = 0,46 и ν2 = 0,46 /12; модуль сдвига для главных направлений упругости 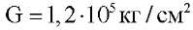 . Пусть длина пластины a = 5, ширина b = 1, края
. Пусть длина пластины a = 5, ширина b = 1, края 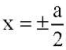 — защемлены, а края
— защемлены, а края 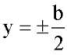 свободны, параметр
свободны, параметр 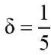 (пластину можно считать длинной), коэффициент постели k = 350. Численный расчет решения задачи (16) с краевыми условиями (17) дает значение критической нагрузки p = 37,42, график соответствующей собственной функции представлен на рис. 3 a. Численный расчет решения задачи (23), (24) при ν1 = 0,46 и k = 350 для балки длиной a = 5 дает p0 = 39,01, при этом собственная функция имеет вид, представленный на рис. 3 б. Как видим, критическая нагрузка потери устойчивости пластины совпадает с критической нагрузкой балки с погрешностью
(пластину можно считать длинной), коэффициент постели k = 350. Численный расчет решения задачи (16) с краевыми условиями (17) дает значение критической нагрузки p = 37,42, график соответствующей собственной функции представлен на рис. 3 a. Численный расчет решения задачи (23), (24) при ν1 = 0,46 и k = 350 для балки длиной a = 5 дает p0 = 39,01, при этом собственная функция имеет вид, представленный на рис. 3 б. Как видим, критическая нагрузка потери устойчивости пластины совпадает с критической нагрузкой балки с погрешностью 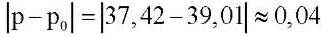 . Собственные функции задач (16), (17) и (23), (24) имеют одинаковое число полуволн.
. Собственные функции задач (16), (17) и (23), (24) имеют одинаковое число полуволн.
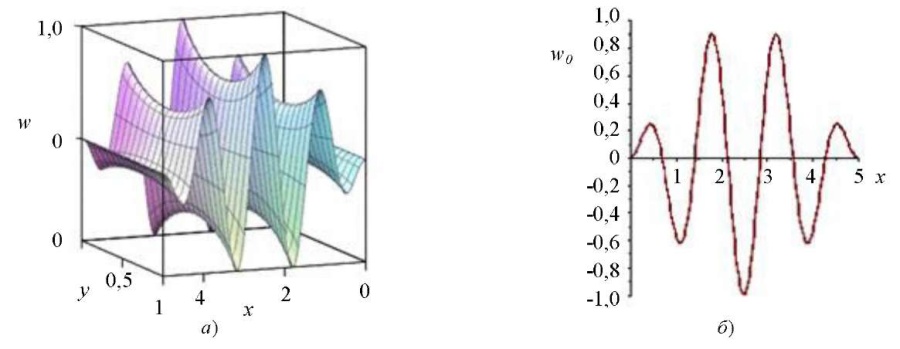
Рис. 3. Формы потери устойчивости: а — w(x,y), сжатой ортотропной длинной пластины; б — w0(x), сжатой балки
Обсуждение и заключения. Исследована задача о критических нагрузках сжатой в двух направлениях ортотропной пластины, лежащей на упругом основании. Задача сведена к решению параметрической линейной краевой задачи на собственные значения. В случае краевых условий подвижного шарнирного опирания приведены точные формулы собственных значений и собственных функций, а в случае свободного защемления краев применен вариационный метод в сочетании с конечно-разностным методом и построена компьютерная программа решения задачи. Получены следующие выводы:
- При повышении составляющей сжимающей нагрузки q вдоль оси y снижается величина критического значения p* нагрузки, сжимающей пластину вдоль оси x.
- Если ортотропная пластина сжимается нагрузкой вдоль направления, которое соответствует большей изгибной жесткости, то критическое значение потери устойчивости больше, чем критическое значение действующей вдоль направления меньшей изгибной жесткости сжимающей нагрузки.
- При наличии упругого основания большему значению коэффициента постели k > 0 соответствует большее значение критического значения сжимающей нагрузки. Наличие упругого основания повышает несущую способность сжатой пластины.
- В случае длинной ортотропной пластины на упругом основании критическую нагрузку сжатой пластины можно вычислять приближенно как критическую нагрузку сжатой балки на упругом основании с модулем упругости, равным модулю упругости пластины в продольном направлении.
Список литературы
1. Зубов, Л. М. Уравнения Кармана для упругой пластинки с дислокациями и дисклинациями / Л. М. Зубов // Доклады академии наук. — 2007. — Т. 412. — С. 343–346.
2. Zubov, L. M. The Linear Theory of Dislocation and Disclinations in Elastic Shells / L. M. Zubov // Journal of Applied Mathematics and Mechanics. — 2010. — Vol. 74. — P. 663–672. https://doi.org/10.1016/j.jappmathmech.2011.01.006
3. Зубов, Л. М. Теория дислокаций и дисклинаций в упругих пластинках / Л. М. Зубов, А. В. Столповский // Прикладная математика и механика. — 2008. — Т. 72. — C. 996–1013.
4. Зубов, Л. М. Сильный изгиб круглой пластинки с непрерывно распределенными дисклинациями / Л. М. Зубов, Фам Тан Хунг // Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. — 2010. — № 4 (158). — С. 28–33.
5. Зубов, Л. М. Осесимметричнный изгиб нелинейно упругой кольцевой пластики с распределенными дисклинациями / Л. М. Зубов, Т. Х. Фам // Экологический вестник научных центров ЧЭС. — 2010. — № 4. — C. 36–43.
6. Папков, С. О. Колебания прямоугольной ортотропной пластины со свободными краями: анализ и решение бесконечной системы / С. О. Папков // Акустический журнал. — 2015. — Т. 61. — С. 152–160. https://doi.org/10.7868/S0320791915010086
7. Столяр, А. М. Поведение узких панелей и сферических оболочек в условиях статического и динамического нагружения. Асимптотический и численный анализ: монография / А. М. Столяр. — Ростов-на-Дону : Издательство Южного федерального университета, 2014. — 146 с.
8. Finiukova, V. O. Asymptotic Integration of One Narrow Plate Problem / V. O. Finiukova, A. M. Stolyar // In book: Shell-like Structures. Non-Classical Theories and Applications. Advanced Structured Materials Series. — 2011. — Vol. 15. — P. 53–62. Springer-Verlag: Berlin – Heidelberg.
9. Пешхоев, И. М. Выпучивание сжатой упругой прямоугольной пластины со свободными краями / И. М. Пешхоев, Б. В. Соболь // Проблемы прочности и пластичности. — 2020. — Т. 82. — С. 244–251. https://doi.org/10.32326/1814-9146-2020-82-2-244-251
10. Пешхоев, И. М. Асимптотика критических нагрузок сжатой узкой упругой пластины с внутренними напряжениями / И. М. Пешхоев // Проблемы прочности и пластичности. — 2021. — Т. 82. — С. 227–234. https://doi.org/10.32326/1814-9146-2021-83-2-227-234
11. Peshkhoev, I. M. Buckling of the Nonuniformly Compressed Plate with Dislocations and Disclinations / I. M. Peshkhoev, A. M. Stolyar // In book: Analysis of Shells, Plates, and Beams. Advanced Structured Materials Series. — 2020. — Vol. 134. — P. 345–366. Springer, Cham. http://dx.doi.org/10.1007/978-3-030-47491-1_18
12. Two-dimensional linear models of multilayered anisotropic plates / A. K. Belyaev, N. F. Morozov, P. E. Tovstik, T. P. Tovstik // Acta Mechanica. — 2019. — Vol. 230. — P. 2891–2904. https://doi.org/10.1007/s00707-019-02405-y
13. Морозов, Н. Ф. О формах потери устойчивости сжатой пластины на упругом основании / Н. Ф. Морозов, П. Е. Товстик // Доклады академии наук. — 2012. — Т. 446. — С. 37–41.
14. Морозов, Н. Ф. Изгибная жесткость многослойных пластин / Н. Ф. Морозов, П. Е. Товстик, Т. П. Товстик // Известия Российской академии наук. Механика твердого тела. — 2020. — № 5. — С. 7–12. https://doi.org/10.31857/S0572329920050128
15. Янковский, А. П. Моделирование термоупруговязкопластического деформирования гибких армированных пластин / А. П. Янковский // Прикладная математика и механика. — 2022. — Т. 86. — С. 121–150. https://doi.org/10.31857/S003282352201009X
16. Altenbach, H. On the Effective Stiffness of Plates Made of Hyperelastic Materials with Initial Stresses / H. Altenbach, V. A. Eremeyev // International Journal of Non-Linear Mechanics. — 2010. — Vol. 45. — P. 976–981. https://doi.org/10.1016/j.ijnonlinmec.2010.04.007
17. Eremeev, V. V. Buckling of a Two-Layered Circular Plate with a Prestressed Layer / V. V. Eremeev, L. M. Zubov // Mathematics and Mechanics of Solids. — 2017. — Vol. 22. — P. 773–781. https://doi.org/10.1177/1081286515612527
18. Altenbach, H. Bending of a Three-Layered Plate with Surface Stresses / H. Altenbach, V. A. Eremeyev // In book: Analysis and Modelling of Advanced Structures and Smart Systems. Advanced Structured Materials Series. — 2018. — Vol. 81. — P. 1–10. Springer: Singapore. https://doi.org/10.1007/978-981-10-6895-9_1.
19. Eremeev, V. V. On Instability of Three-Layered Nonlinear Elastic Rectangular Plate with Prestressed Middle Layer / V. V. Eremeev, L. M. Zubov // In book: Shell Structures: Theory and Applications. — 2018. — Vol. 4. — P. 215–218. London: CRC Press, Taylor and Francis Group.
Об авторах
И. М. ПешхоевRussian Federation
Пешхоев Иса Мусаевич, доцент кафедры «Информационные технологии», кандидат физико-математических наук, доцент
344003, РФ, г. Ростов-на-Дону, пл. Гагарина, 1
Б. В. Соболь
Russian Federation
Соболь Борис Владимирович, заведующий кафедрой «Информационные технологии», доктор технических наук, профессор
344003, РФ, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Пешхоев И.М., Соболь Б.В. Критические нагрузки равномерно сжатой ортотропной прямоугольной пластины на упругом основании. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):214-223. https://doi.org/10.23947/2687-1653-2022-22-3-214-223
For citation:
Peshkhoev I.M., Sobol B.V. Critical Loads of Uniformly Compressed Orthotropic Rectangular Plate on an Elastic Base. Advanced Engineering Research (Rostov-on-Don). 2022;22(3):214-223. https://doi.org/10.23947/2687-1653-2022-22-3-214-223
JATS XML














































