Scroll to:
Validation of Reliability Indices during Experimental Development of a Complex Technical Series System
https://doi.org/10.23947/2687-1653-2023-23-1-26-33
Abstract
Introduction. The article studies the problem of validating the specified levels of reliability during experimental development of a complex technical series system. Such tasks arise when it is required to make a decision on testing the system as part of a larger one or on the completion of experimental development and the start of series production. The study is aimed at validating the reduction of the experimental development time. The task is to determine whether the hypothesis Но is accepted or rejected.
Materials and Methods. To implement the research objective and task, a critical area described by the inequality was constructed based on the test results. The formulation of the requirements validation task was based on well-known approaches to testing statistical hypotheses. The conceptual apparatus of information theory, probability, and statistics was involved. The theoretical and applied literature on mathematical methods in reliability theory was studied. The particular tasks of the work were solved by known ways. Thus, the probability of obtaining the exact number of successful outcomes in a certain number of experiments was determined by the Bernoulli scheme. The exact confidence interval based on the binomial distribution was derived from the Clopper-Pearson relation. The theorem of A.D. Solovyov and R. A. Mirny made it possible to assess the system reliability based on the test results of its components.
Results. Control rules adequate to the stage of experimental development (with insufficient data on the technical system) and the stage of series production were mathematically defined. The probability of a successful outcome when testing technical systems was represented by:
– the probability of event for a system element;
– confidence value;
– required scope of tests.
In these terms, the null and alternative hypotheses and the corresponding reliability control procedures were investigated. Two provisions were considered. The first one provided using the null confidence hypothesis Но = {Р ≥ РТ} and an alternative Н = { Р < РТ} to confirm the requirements (РТ, γ) for the reliability indicator of one parameter for any (РТ, γ). In this case, one trouble-free test was enough. The second provision considered a sequential technical system with independent elements that were tested separately from the system according to the Bernoulli scheme for one parameter. We considered the requirements for the system in the form of a set of values (РТ, γ) and the requirements for any of its elements (РТi, γ). They coincided when the planned outcome of the tests corresponded to the cases when the ratio Р= lim 1≤i≤N : Р i = Р m was fulfilled, and the null alternative hypothesis was selected from the theory of statistical hypothesis testing.
Discussion and Conclusions. The experimental development strategy should be implemented in two stages: the search and validation of the reliability of the elements through a series of fail-safe tests. In this case, the planned scope of tests of each element is determined taking into account the confidence probability, the lower limit of the confidence interval, and the requirements for reliability indices of one parameter of the technical system. If the use of the null confidence hypothesis is acceptable, one fail-safe test is sufficient to confirm the requirements for the reliability index.
Keywords
For citations:
Tsarev O.Yu., Tsarev Yu.A. Validation of Reliability Indices during Experimental Development of a Complex Technical Series System. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):26-33. https://doi.org/10.23947/2687-1653-2023-23-1-26-33
Introduction. Rational methods of validating the specified reliability levels are of current concern for experimental testing of a complex technical system when a decision is made on the possibility of testing it as part of a larger structure or on the completion of experimental development and the start of series production. The same tasks arise during series production, if it is required:
- to assess the readiness of the enterprise to produce series products based on the test data of the pilot batch;
- to make a conclusion about the compliance of the products with the requirements of technical documentation, taking into account the operating data.
The study objective was to obtain an acceptable solution for planning and reducing the scope of tests using methods of interval estimation of reliability indices of sequential technical systems. To achieve the stated goal, it was required to determine whether hypothesis Но was accepted or rejected.
Materials and Methods. It is reasonable to formulate the task of validating the requirements in terms of the theory of statistical hypothesis testing [1–4]. Let Р be the reliability of the technical system, РТ — some fixed (required) level for Р. Prior to testing about Р, three initial assumptions can be made: 
Each of them is called a null hypothesis if it is written as:

Set  contains only one element, therefore, hypothesis
contains only one element, therefore, hypothesis  is called simple. Hypotheses of the form
is called simple. Hypotheses of the form  and
and  are called complex. Along with the null hypothesis expressing a pre-formulated point of view, an alternative hypothesis Н is specified expressing the opposite statement
are called complex. Along with the null hypothesis expressing a pre-formulated point of view, an alternative hypothesis Н is specified expressing the opposite statement  We use the conceptual apparatus of the theory of information [1], probability and statistics, applicable to solving such problems. Consider two aggregates of sets Но and Н:
We use the conceptual apparatus of the theory of information [1], probability and statistics, applicable to solving such problems. Consider two aggregates of sets Но and Н:

Hypothesis Но in (1) will be called rigid, or the distrust hypothesis. Indeed, in case (1), initially (before the test), we proceed from a position of distrust of the quality level of the system. Reliability index Р is assumed to be no higher than a certain fixed level Р’Т . Hypothesis Но in (2) will be called the confidence hypothesis, since in this case, it is initially assumed that reliability index Р is not less than some fixed value РТ.
The meaning of values Р’Т and РТ is different. In (1), Р’Т — such a rejected value that at Р Р’Т , the system is considered unacceptable. In (2), РТ — such a value that at Р
Р’Т , the system is considered unacceptable. In (2), РТ — such a value that at Р Р’Т , the system is considered acceptable for use. Obviously, РТ>Р’Т.
Р’Т , the system is considered acceptable for use. Obviously, РТ>Р’Т.
Research Results. Thus, it is required to determine whether hypothesis Но is accepted or rejected. In the theory of statistical hypotheses, a critical area is constructed for this purpose based on the test results. It is described by some inequality. Moreover, the null hypothesis (due to the initial confidence in it) is adhered to as long as it is reasonable from the point of view of the accepted level of significance α. Therefore, as is already clear that the reliability control procedure in case (1) will be significantly different compared to case (2).
Indeed, we will further make sure that to reject hypothesis Но in (1) and accept hypothesis  of meeting the requirement for reliability indices, a critical area (or condition) should be used
of meeting the requirement for reliability indices, a critical area (or condition) should be used
 (3)
(3)
where  — the lower bound of the confidence interval for Р at the value of the confidence probability γ = 1 – α. ;
— the lower bound of the confidence interval for Р at the value of the confidence probability γ = 1 – α. ;  — the lower bound of the rejected interval for Р at the value of confidence probability γ = 1 – α..
— the lower bound of the rejected interval for Р at the value of confidence probability γ = 1 – α..
In case (2), the condition should be used to accept hypothesis Но about the compliance of the value of parameter Р to the requirement
 (4)
(4)
where  — the upper bound of the confidence interval for Р at the value of the confidence probability γ = 1 – α.
— the upper bound of the confidence interval for Р at the value of the confidence probability γ = 1 – α.
In (3) and (4), the requirement for the reliability index of one parameter Р is understood as a set of values  or
or  given before testing.
given before testing.
Let one successful test be carried out under the conditions of the Bernoulli scheme. Then, using the Clopper-Pearson relations, we find the lower and upper bounds of one parameter with the value, for example, γ = 0.95:

Here, even for very moderate values  , condition (3) is not fulfilled, while (4) is fulfilled at any РТ. Let us show the validity of the accepted position.
, condition (3) is not fulfilled, while (4) is fulfilled at any РТ. Let us show the validity of the accepted position.
First position. If it is permissible to use the null confidence hypothesis 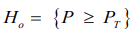 with alternative
with alternative  then one fail-safe test is sufficient to confirm the requirements
then one fail-safe test is sufficient to confirm the requirements 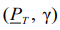 for the reliability index of one parameter for any
for the reliability index of one parameter for any 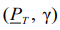 .
.
If the initial hypothesis Но is the hypothesis of distrust from (1), then a significantly larger number of tests are needed. Thus, for m = 0, we get  This is quite fair, because, when testing hypotheses, they initially proceed from the validity of the null hypothesis Но.
This is quite fair, because, when testing hypotheses, they initially proceed from the validity of the null hypothesis Но.
At the stage of experimental development, there are no sufficiently complete data, therefore, it is reasonable to use control rule (3). At the stage of series production, one can proceed from the confidence hypothesis and use a significantly easier control rule (4). This is acceptable if, according to the experimental testing, condition (3) was fulfilled.
Consider a system consisting of N independent elements connected in series, which can be tested separately. Then, the probability of a successful outcome when testing technical systems:
 (5)
(5)
Here, Рi — probability of the same event for the i-th element. The requirements for value Р are specified in the form of a set of values 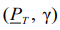 . It is required to plan a procedure for monitoring the reliability of one parameter for each element of the system, i.e., to specify
. It is required to plan a procedure for monitoring the reliability of one parameter for each element of the system, i.e., to specify  a pair
a pair 
Due to the multiplication of Рi in formula (5), ratio  must be fulfilled. Besides, γ=γi.
must be fulfilled. Besides, γ=γi.
As a result, the required scope of tests ni of each element increases dramatically, and even with fail-safe results of all tests, it becomes unacceptable. At 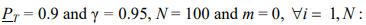

This method of planning is logically contradicted by inequality  , following from
, following from  when mi = 0. It is clear that with fail-safe outcomes, the required scope of tests nоi of i-th element, conducted separately from the system, should be equal to the required scope of tests of system nо. To avoid this contradiction, the theorems of A.D. Solovyov and R.A. Mirny should be used [5–7]. Thus, when m = 0,
when mi = 0. It is clear that with fail-safe outcomes, the required scope of tests nоi of i-th element, conducted separately from the system, should be equal to the required scope of tests of system nо. To avoid this contradiction, the theorems of A.D. Solovyov and R.A. Mirny should be used [5–7]. Thus, when m = 0, 

Here,  — the lower bound of the confidence interval for the reliability index of a technical system by one parameter, at value γ of the confidence probability;
— the lower bound of the confidence interval for the reliability index of a technical system by one parameter, at value γ of the confidence probability;  i — the value of the lower bound of the confidence interval for the reliability index of the i-th element of the system with the same confidence probability; n — minimum number of tests of system elements; f (n, 0, γ) — the root of the Clopper-Pearson equation:
i — the value of the lower bound of the confidence interval for the reliability index of the i-th element of the system with the same confidence probability; n — minimum number of tests of system elements; f (n, 0, γ) — the root of the Clopper-Pearson equation:

In all the cases mentioned (9), the lower bounds are not multiplied, and the system degenerates into one weakest element. This provides validating the following position.
Second position. Consider a sequential system with N independent elements that are tested separately from the system according to the Bernoulli scheme for one parameter. The requirements specified for the system in the form of a set of values (  Т, γ) , and the requirements for any of its elements (
Т, γ) , and the requirements for any of its elements (  Тi, γ) coincide if the planned outcome of the tests corresponds to the mentioned cases of fulfillment of ratio (9), and the null alternative hypothesis is selected based on (1) and (2).
Тi, γ) coincide if the planned outcome of the tests corresponds to the mentioned cases of fulfillment of ratio (9), and the null alternative hypothesis is selected based on (1) and (2).
Consequence. In case of (3), execution of (9) — the planned scope of fail–safe tests (N – 1) of elements, it is determined from:
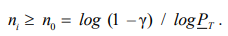 (10)
(10)

From here:

Ratios (10) and (15) make it possible to plan the required scope of testing of the i-th element of the technical system with a certain sequence of experimental development of the system. The whole process of experimental development is divided conditionally into two periods: the search and validation of reliability requirements for a decision on the transition to the next stage of testing or on the acceptance of a technical system for series production. In the first period, improvements are possible, and it is reasonable to use models with a variable probability P of a successful outcome of the system test.
The data obtained in the first period can be used to calculate value РН.
In the second period, we deal with an established version of the design of the technical system and technological process. This makes it possible to use the binomial type test models discussed above with constant probability Р.
Let the first period of developing N elements of the technical system be completed, then, the question is raised about validating the requirements for the reliability index of the system by one parameter. It is reasonable to validate reliability if a positive decision is made only in case of a fail-safe outcome of the last series of tests for each of N elements. This strategy is convenient because it is based on the minimum possible number of tests of elements of the technical system and provides simple analytical solutions (10) and (15).
In general, it makes sense to investigate a strategy that allows for failures of elements during testing and is based on optimization of some objective function. But here, we restrict ourselves to considering only the mentioned strategy with fail-safe final series.
Discussion and Conclusions. The results of scientific research allowed us to formulate the following conclusions.
1. Even with a large number of N elements of the system, it is possible to plan the scope of their tests. In this case, the methods of interval estimation of reliability indices of sequential technical systems provide obtaining an acceptable solution, but only for one parameter.
2. The strategy of experimental development of technical systems is closely related to the method of validating the reliability of elements. The rational strategy of experimental development provides for confirmation of the reliability of the elements after the search period through a final series of fail-safe tests. In this case, the planned scope of tests of each of N elements does not depend on N and is determined by ratio (15), which includes the requirements ( Т, γ) for the reliability indices of one parameter of the technical system as a whole and РН. The scope of tests obtained by (15) for each element of the technical system, for any number of them, is small if moderate requirements (
Т, γ) for the reliability indices of one parameter of the technical system as a whole and РН. The scope of tests obtained by (15) for each element of the technical system, for any number of them, is small if moderate requirements ( Т = 0.80 …0.95; γ = 0.90 … 0.95) are specified for a system of N elements, but only for one parameter. At the same time, the scope decreases with increasing value РН.
Т = 0.80 …0.95; γ = 0.90 … 0.95) are specified for a system of N elements, but only for one parameter. At the same time, the scope decreases with increasing value РН.
3. In series production, when testing upgraded technical systems, it is possible to use a control method with null and alternative hypothesis change. If the use of the null confidence hypothesis is acceptable, then one fail-safe test is sufficient to validate the requirements for the reliability index.
References
1. Belov VM, Novikov SN, Solonskaya OI. Teoriya informatsii. Moscow: GLT; 2012. 143 p. (In Russ.)
2. Godin AM. Statistika. Moscow: Dashkov i K°; 2016. 451 p. (In Russ.)
3. Müller K. The New Science of Cybernetics: A Primer. Journal of Systemics, Cybernetics and Informatics. 2013;11:32–46.
4. Hamdy A Taha. Operations Research: An Introduction, 9th ed. New York: Prentice Hall; 2011. 813 p.
5. Pavlov IV. Confidence Limits for System Reliability Indices with Increasing Function of Failure Intensity. Journal of Machinery Manufacture and Reliability. 2017;2:70–75.
6. Gnedenko BV, Belyaev YuK, Solovyev AD. Matematicheskie metody v teorii nadezhnosti. Moscow: Librokom; 2013. 584 p. (In Russ.)
7. Betsch S, Ebner B. Fixed Point Characterizations of Continuous Univariate Probability Distributions and their Applications. Annals of the Institute of Statistical Mathematics. 2021;73:31–59. https://doi.org/10.48550/arXiv.1810.06226
8. Nakakita SH, Kaino Y, Uchida M. Quasi-Likelihood Analysis and Bayes-Type Estimators of an Ergodic Diffusion Plus Noise. Annals of the Institute of Statistical Mathematics. 2021;73:177–225. https://doi.org/10.1007/s10463-020-00746-3
9. Pavlov IV, Razgulyaev SV. Lower Confidence Limit for Mean Time between Failures in a System Featuring Repairable Components. Herald of the Bauman Moscow State Technical University, Series: Natural Sciences. 2018;5:37–44. http://dx.doi.org/10.18698/1812-3368-2018-5-37-44
10. Fishwick P. (ed.) Handbook of Dynamic Systems Modeling. New York: CRC Press; 2007. 760 p. https://doi.org/10.1201/9781420010855
11. Antonov AV, Malovik KN, Chumakov IA. Interval Estimation of the Reliability Characteristics for Unique Equipment. Fundamental Research. 2011;12(1):71–76.
12. Gvozdev VE, Abdrafikov MA, Akhunyanova KB. Interval Estimation of Reliability Parameters Based on Methodology FMEA. Vestnik UGATU. 2014;65:91–98.
About the Authors
O. Yu. TsarevRussian Federation
Oleg Yu Tsarev, consultant “Business Solutions and Technologies”
5B, Lesnaya St., Moscow, 127055
Yu. A. Tsarev
Russian Federation
Yury A Tsarev, professor of the Engineering and Maintenance of Transporting and Manufacturing Systems Department
1, Gagarin sq., Rostov-on-Don, 344003
Review
For citations:
Tsarev O.Yu., Tsarev Yu.A. Validation of Reliability Indices during Experimental Development of a Complex Technical Series System. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):26-33. https://doi.org/10.23947/2687-1653-2023-23-1-26-33
JATS XML














































