Перейти к:
Оценка появления начальных разрушений от концентраторов напряжений в сварных соединениях и элементах конструкций
https://doi.org/10.23947/2687-1653-2023-23-1-41-54
Аннотация
Введение. Данные о возникновении начальных разрушений, полученные испытаниями на стандартных образцах, не всегда можно экстраполировать на реальные сварные соединения и конструкции. Это обусловлено отличиями концентраторов в соединениях, т. к. после сварки возникает значительная структурно-механическая неоднородность зоны термического влияния и концентраторов напряжений. Протяженные, глубокие концентраторы рассматриваются как трещиноподобные дефекты, в вершинах которых образуется объемное, сложное напряженное состояние. Решается вопрос построения критических диаграмм начала возникновения предельного состояния в вершине концентратора, которое зависит от уровня внешней нагрузки и теоретического коэффициента концентрации.
Материалы и методы. Для исследования напряженного состояния задействовали аналитические методы. Проанализирована литература по теме. Учтены особенности проверенных физических моделей и закономерности поведения материалов. Характеристики сплавов стали взяты из открытых источников и обобщены в виде таблицы. Нелинейные уравнения решались в прикладных программах Matlab. Построенные авторами диаграммы позволяют отследить корреляцию опасного уровня теоретического коэффициента концентрации напряжений и уровня внешней нагрузки. Для оформления графической части работы использовали Curve Fitting Toolbox Matlab.
Результаты исследования. Дана характеристика разрушений от концентраторов напряжений в сварных соединениях. Наглядно показано развитие трещин в зоне сплавления. Указаны условия, стимулирующие и тормозящие разрушение. Определен теоретический коэффициент концентрации напряжений α𝑇. Показано, каким образом данный показатель зависит от ширины, высоты шва и от толщины свариваемой детали. Рассмотрены острые концентраторы напряжений с теоретическим коэффициентом концентрации αт= 5…14 и более. Для этого случая приводится аппроксимирующая формула, которая учитывает максимальное напряжение в концентраторе в первом полуцикле, исходную деформацию и коэффициент асимметрии цикла нагружения. Через эти элементы задается показатель повышения максимальных напряжений в зависимости от числа циклов нагружения. Аналитически показаны условие текучести, напряженное состояние и коэффициент перенапряжения, учитывающий повышение первого главного напряжения для сложного напряженного состояния. Описана модель критического состояния в вершине острого макроконцентратора напряжений. Она представлена как зависимость относительных напряжений зарождения разрушения σн𝑏𝑐/σ0,2 от концентратора. Проанализированы возможные вариации этой модели. Представлены зависимости относительных значений σ𝐻𝑏𝑐⁄ σ0,2 от теоретического коэффициента концентрации α𝑇𝑏𝑐=α𝑇. Для проверки физической адекватности данной модели построены графики, которые отражают изменения относительного напряжения внешней нагрузки при критическом состоянии в вершине концентратора напряжений. Обоснована неизбежность бифуркации как результата исследуемых процессов. Указаны два направления дальнейшего развития событий: хрупкое разрушение и потеря устойчивости напряженного состояния с переходом к росту пластических деформаций. Момент бифуркации определен как критическое состояние в очаге концентратора.
Обсуждение и заключения. Анализ и расчеты, выполненные в рамках представленной научной работы, позволили, в частности, сделать выводы о роли ключевых факторов исследуемых процессов. Установлено, например, что работа сплава стали при высоком теоретическом коэффициенте концентрации напряжений зависит от характеристик напряженного состояния. При жестком состоянии возможно сдерживание сдвиговой деформации и наступление предельного состояния при меньшем значении теоретического коэффициента концентрации напряжений. При обычной прочности стали (в сравнении с высокой) фиксируется большее влияние объемности напряженного состояния на значение теоретического коэффициента концентрации напряжений. Вероятность разрушения зависит от сопротивляемости материала росту макротрещины. В будущих изысканиях возможно уточнение аналитических моделей и результатов, оценка эффективных коэффициентов концентрации напряжений.
Ключевые слова
Для цитирования:
Молоков К.А., Новиков В.В., Дабалез М. Оценка появления начальных разрушений от концентраторов напряжений в сварных соединениях и элементах конструкций. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):41-54. https://doi.org/10.23947/2687-1653-2023-23-1-41-54
For citation:
Molokov K.А., Novikov V.V., Dabalez M. Evaluation of the Occurrence of Initial Failures from Stress Concentrators in Welded Joints and Structural Elements. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):41-54. https://doi.org/10.23947/2687-1653-2023-23-1-41-54
Введение. Статическая и усталостная прочность снижается из-за дефектов сварных соединений. Это могут быть:
- трещины, образовавшиеся во время или после сварки;
- концентраторы напряжений (подрезы, несплавления, поры, сварочные кратеры, высокая чешуйчатость, резкое изменение формы шва, наплывы и др.).
В последнем случае определяющими будут:
- форма, размер концентратора и положение в сварном соединении;
- показатель напряженного состояния в вершине [1].
При циклических нагрузках в сварных соединениях часто возникают и развиваются трещины, спровоцированные концентраторами напряжений [2]. Риск зависит еще и от того, насколько напряженное состояние сварного соединения с концентратором близко к возникновению макротрещины и распространению ее при рабочих σ𝐻 и циклических нагрузках σ−1. Очевидно, что последнее существенно зависит от размеров, формы макродефекта и напряженного состояния в его вершине. Например, продолговатый и узкий макроконцентратор напряжений опаснее, чем округлый. Вероятно, в его вершине сразу образуется трещина, и вместе с ней исходный концентратор будет представлять одну длинную макротрещину [3]. Величина такой «общей» макротрещины может оказаться критической, что снизит статическую прочность [4]. Это зависит от ее длины и механических характеристик материала в вершине исходного концентратора.
Цель исследования — разработка аналитической модели оценки опасного уровня концентрации напряжений. Речь идет об образовании трещины в вершине концентратора, резком снижении несущей способности сварных соединений и деталей конструкций.
Материалы и методы. Научные изыскания в рамках заявленной темы базировались на известных физических моделях и закономерностях поведения материалов. Проанализирована теоретическая и прикладная литература. Из источников извлечены иллюстративные и справочные материалы.
Напряженное состояние исследовалось аналитическими методами. Выявлялась взаимосвязь жесткости напряженного состояния и величины теоретического коэффициента концентрации напряжений. Результаты представлены в виде диаграмм. Такой способ визуализации дает возможность отследить корреляцию опасного уровня внешней нагрузки и теоретического коэффициента концентрации напряжений.
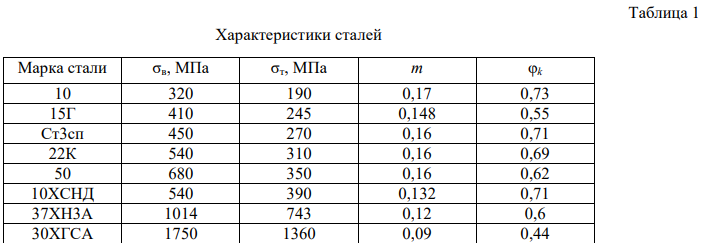
Для проверки результатов расчетов по физической адекватности авторской модели строились графики зависимостей для критического состояния. В работе использованы сведения о широко распространенных конструкционных сталях феррито-перлитного класса в состоянии поставки (сталь 10, 22К, 50, Ст3сп, 37ХН3А, 30ХГСА и др.). Их механические характеристики получены из открытых источников1 и обобщены в таблице 1.
Данные визуализировали в Curve Fitting Toolbox Matlab.
Для вывода формул задействовали математический аппарат. При решении нелинейных уравнений использовали пакет прикладных программ Matlab.
Результаты исследования
Характеристика разрушений от концентраторов напряжений в сварных соединениях. С начала 2000-х годов исследуются концентрации напряжений в сварных соединениях и конструкциях применительно к промышленным задачам [2–3, 5–9].
Примеры разрушений сварных соединений из-за концентрации напряжений приведены на рис. 1.

Рис. 1. Разрушения крестовых и стыковых соединений2 от концентраторов напряжений: а, е — от зоны непроплавления, без разделки кромок; б — от подреза, с разделкой кромок; в — от резкого перехода в зоне сплавления; г — подрез; д — от концентратора, образованного ступенчатым переходом в стыке кромок [10]
Разрушение крестовых соединений с большим непроплавлением кромок (обозначено стрелками на рис. 1 а) возможно при нагрузках:
- статических (в результате охрупчивания зоны сплавления);
- циклических (вызывают образование трещин в вершинах концентратора).
В [5] анализируется распределение напряжений для стыковых, угловых, крестовых соединений и прерывистых связей судовых конструкций. В стыковых и крестовых сварных соединениях особое значение имеет область основного металла, примыкающая к сварному шву. Это самое слабое сечение, определяющее прочность соединения при переменных напряжениях. Следует отметить, что швы всегда достаточно длинны по сравнению с толщиной металла и концентратором напряжения (подрезом в стыковом или крестовом соединении). Это препятствует сдвигу в области концентратора и создает двухосное, а чаще многоосное напряженное состояние [11][12]. При рассмотрении разрушения сварных швов с концентраторами (рис. 1 а, д, е) учтем концепцию возникновения пластической деформации в области вершины [5][7]. Кроме того, отметим, что концентраторы примыкают к зоне сплавления, которая после сварки испытывает продольные остаточные напряжения растяжения. Они влияют на степень жесткости напряженного состояния в очаге концентратора [1][13–14]. Все это препятствует прохождению сдвига в очаге концентратора и может способствовать возникновению минимальной хрупкой макротрещины при высоком теоретическом коэффициенте концентрации напряжений αт даже от статической нагрузки.
В [9] описаны показательные разрушения от сварных дефектов в трубопроводах большого диаметра. Установлено, что при длительной эксплуатации (более 20 лет) появляются трещины усталости в подрезах продольных сварных соединений труб. Трещины в подрезах в зоне сплавления, как правило, разветвляются и распространяются по двум направлениям (рис. 2): одна отдаляется от зоны сплавления, другая развивается по зоне сплавления (по шву). Это говорит о существенном влиянии механических, структурных характеристик материала3 и механохимической неоднородности на процесс распространения начального разрушения [13, 14]. С другой стороны, разветвление трещины может затруднять процесс дальнейшего разрушения и переход трещины в магистральную.
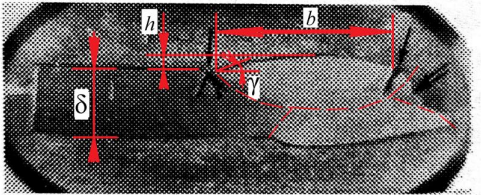
Рис. 2. Разрушение в сварном соединении трубы от концентрации напряжений в зоне сплавления. Сталь 14ХГС. Одинарной стрелкой показаны усталостные трещины; двойной — кромка разрыва трубы; штрихами — очертания сварного шва. Здесь b — ширина шва; h — высота шва; δ — толщина свариваемой детали; γ — угол перехода от основного металла к шву [9]
Теоретический коэффициент концентрации напряжений в зоне сплавления можно определить по формуле, учитывающей эффект концентрации от неплавного перехода в этой зоне [5]:
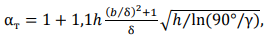 (1)
(1)
где γ = 𝐴[ 90 exp(−ρ⁄ρ0) + 𝐵] — угол перехода от основного металла к шву; ρ — радиус перехода от основного металла к шву; ρ0 = 1 мм; 𝐴 = 0,94 … 0,17; 𝐵 = 0,8; 𝑏 — ширина шва; ℎ — высота шва; δ — толщина свариваемой детали (рис. 2).
Однако данная зависимость не учитывает измененные механические характеристики материала. В этих зонах обычно присутствуют закалочные структуры, механические характеристики которых могут значительно (до 30 %) отличаться от характеристик шва и основного металла.
Можно косвенно контролировать трещинообразование и напряженное состояние в области вершины концентратора напряжений через коэффициент концентрации их интенсивности. Так, при разрушении образца от усталости, в вершине концентратора образуется одна макротрещина, а в коррозионной среде — группа (рис. 3).

Рис. 3. Усталостное разрушение стали 45 от V-образного концентратора напряжений: а — на воздухе; б — в воде — коррозионной среде. Увеличение в 134 раза4
После образования группы макротрещин (рис. 3 б) роль макроконцентратора снижается, и дальнейшее развитие разрушения может быть приостановлено либо заторможено. Это подтвердили эксперименты, которые свидетельствуют о росте усталостной прочности в образцах с концентрацией напряжений в коррозионной среде5. Такая группа трещин как бы разрыхляет материал, изменяет напряженное состояние над поверхностью и под ней в вершине макроконцентратора, что препятствует образованию лидирующей трещины, способной развиваться далее при меньшем уровне циклических нагрузок.
Рассмотрим ситуацию на поверхности или в толще металла в массивных телах под напряжениями σ𝐻 на бесконечности при плосконапряженном состоянии. В этом случае целесообразно использовать решение Колосова и Инглиса для концентратора эллиптической формы:
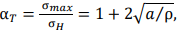 (2)
(2)
где ρ и σ𝑚𝑎𝑥 — радиус кривизны и максимальная компонента напряжений на поверхности соответственно, в вершине выреза; 𝑎 — большая полуось эллипса, или половина наибольшей длины области, перпендикулярной направлению поля внешней нагрузки.
Зависимость (2) хорошо согласовывается с инженерной практикой. В соответствии с принятой концепцией теоретический коэффициент концентрации напряжений у выреза определяется глубиной выреза и радиусом кривизны контура в его вершине, но не зависит от формы контура [15].
Благодаря развитию информационных технологий оценка теоретического коэффициента концентрации напряжений не представляет больших трудностей. Результаты по расчетам концентрации напряжений и деформаций в упругой и упругопластической постановке задачи можно получить средствами конечноэлементного анализа CAE [16–18][12].
Эксперименты показали, что при определенной концентрации напряжений, внешней статической нагрузке и упругопластической стадии материала в вершине концентратора на некотором расстоянии от поверхности возникала начальная трещина разрушения. Она быстро распространялась к оси, перпендикулярной направлению растяжения пластин с надрезами. Распространение видно на снимках (рис. 4). Процесс зафиксирован в пластинах при плоском напряженном состоянии и при плоской деформации. В последнем случае появление трещины в толще металла под поверхностью выявили с помощью ультразвукового дефектоскопа.
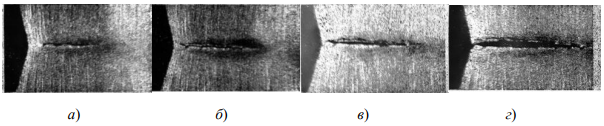
Рис. 4. Зарождение подповерхностной трещины в вершине концентратора при статическом растяжении: а — начало возникновения макротрещины; б, в —увеличение размера вглубь и к поверхности; г — выход трещины на поверхность [19]
Таким образом, при указанных состояниях и достаточно остром концентраторе напряжений образуется зона многоосного напряженного состояния, в которой возможно нарушение сплошности. Здесь будет выше уровень наступления текучести, а предел прочности в ослабленном месте из-за концентратора может увеличиться до 20–60 % (это зависит от материала) [11].
Концентрация напряжений и условия напряженного состояния. Рассмотрим достаточно острые концентраторы напряжений с теоретическим коэффициентом концентрации αт = 5 … 14 и более. Как правило, в роли таких концентраторов выступают упомянутые выше дефекты. В вершине концентратора напряженное состояние можно рассматривать таким же, как при плоской деформации. В [18] приводятся результаты аналитического решения и экспериментальные данные для острых концентраторов при плоской деформации, устанавливается область допустимых значений [α𝑇] и радиус в вершине [ρ] для стали 09Г2С. Однако не описано влияние ее механических характеристик. К тому же не ясно, основаны ли аналитические решения на таких исходных параметрах 09Г2С, как коэффициент упрочнения 𝑚, предел текучести σ0,2, предел прочности σ𝐵, критическое сужение при разрушении φ𝑘 и др. Известно, что пластичность и прочность существенно влияют на уровень допустимой концентрации напряжений и возникновение хрупкого разрушения в вершине.
Для упрочняющихся материалов циклические напряжения в вершине острого концентратора усугубляют возможность возникновения хрупкого разрушения, поэтому за критерий опасности примем такой α𝑇, при котором вероятно возникновение хрупкого разрушения в условиях статической нагрузки. Повышение максимальных напряжений в зависимости от числа циклов нагружения 𝑁 задается аппроксимирующей формулой:
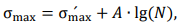 (3)
(3)
где σ′max — максимальное напряжение в концентраторе в первом полуцикле; 𝐴 — коэффициент, зависящий от уровня исходной деформации и коэффициента асимметрии цикла нагружения в вершине концентратора.
Принимаем очевидное допущение, что появление хрупкого разрушения может быть обусловлено следующими причинами:
- усиление интенсивности трехмерного растяжения в непосредственной близости к вершине концентратора;
- увеличение сопротивления пластической деформации материала вблизи вершины как последствие сопротивления сдвигу в острых концентраторах напряжения.
Последнее обстоятельство оказывается тем сильнее, чем выше скорость нагружения и острее концентратор напряжений.
Рассмотрим упругопластическое плоское напряжение в вершине концентратора и упругое состояние в сечении брутто: σ𝑚𝑎𝑥 = αTσH ≫ σ0,2, σ𝐻 ≈ σ0,2 и σ𝐻 < σ0,2. Здесь σ0,2 — условный предел текучести материала при одноосном растяжении. При αт = 7,3 жесткость напряженного состояния близка к состоянию для трещины.
Коэффициент безопасности 𝑚𝐹𝐴𝐷 для трещиноподобного дефекта при плоской деформации незначительно (в переделах 10 %) отличается от ̅𝑚̅̅𝐹𝐴𝐷 ̅̅̅̅для трещины, т. е. для такого состояния, когда имеет место приближенное равенство 𝑚𝐹𝐴𝐷 ≈ 𝑚̅̅̅𝐹𝐴𝐷 ̅̅̅̅:
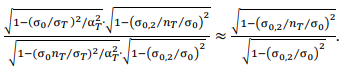 (4)
(4)
Здесь 𝑛𝑇 — коэффициент запаса по пределу текучести, σ0 — локальная прочность материала у вершины трещины или острого концентратора.
В [11] термин «локальный предел текучести» применяется к острым концентраторам напряжения, когда примыкающая к вершине область концентратора испытывает сложное напряженное состояние (СНС). Очевидно, что этим термином обозначается напряжение течения материала на контуре концентратора. На поверхности в его вершине будет плоское напряженное состояние, под поверхностью возникнет трехосное СНС. Там резко возрастет жесткость напряженного состояния, поэтому начальное разрушение сплошности образуется на некотором расстоянии от поверхности (рис. 4). Установлено, что начало наступления локальной текучести в зоне концентратора напряжения не совпадает с уровнем, определенным расчетами по критериям прочности, в частности по Мизесу — Губеру — Генки. При увеличении концентрации напряжений возрастает разница между:
- величиной предела текучести σ0,2, теоретически рассчитанной по этому критерию;
- экспериментально определенной величиной напряжения локального течения материала 0,2∗ в области, примыкающей к вершине концентратора.
Результаты экспериментов на плоских образцах разных сталей и сплавов [11][16] показывают, что отношение σ∗0,2 ⁄σ0,2 хорошо аппроксимируется линейной зависимостью от α𝑇. Тогда условие текучести можно записать в виде:
σ𝑖 = σ0,2(0,9 + 0,1αт), (5)
где σ𝑖 — интенсивность напряжений по Мизесу.
Авторы ограничились экспериментальными исследованиями до значений α𝑇 = 10, и испытания проводились только на плоских образцах с центрально расположенными концентраторами. При плоской деформации жесткость напряженного состояния оказывается несколько выше. Поэтому логично предположить, что текучесть при некоторых значениях α𝑇 наступала бы не раньше, чем при плоском напряженном состоянии. И вполне вероятно, что наклон прямой по уравнению (5) мог быть несколько иным [11]. Тем не менее, остановимся на этой зависимости.
Для момента начала текучести предположим, что с переходом от упругих деформаций к упругопластическим не меняется отношение второго и третьего главного напряжения к первому σ1 = σmax. Это доказано экспериментально.
Приравняем к (5) интенсивность напряжений начала текучести по Мизесу согласно четвертой (энергетической) теории прочности и введем коэффициенты отношений между главными напряжениями при плоской деформации: σ1 = σ𝑖 𝐷; σ2 = 𝑞σ1; σ3 = μ𝑇 ⁄ (1 + 𝑞)σ1 [15]. Здесь μ𝑇 = 0,5 — коэффициент Пуассона в пластической области, а 𝐷 — коэффициент перенапряжения, учитывающий повышение первого главного напряжения в случае СНС. У полученного относительно 𝑞 уравнения два решения. Первое — для растягивающей σ2 компоненты, второе — для сжимающей. Растягивающая компонента σ2 увеличивает жесткость напряженного состояния в случае СНС. После преобразований и сокращений можем выразить ее так:
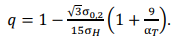 (6)
(6)
Для предельного случая σ𝐻 = 0,2 можно пренебречь изменением радиуса в вершине концентратора и наступлением некоторой начальной глобальной текучести для сечения нетто. Тогда единственное значение α𝑇, удовлетворяющее жесткости эквивалентного трещине напряженного состояния, равно 7,3. Это подтверждает полученное ранее примерное равенство (4). Для других значений, как видно из (6), пропорциональность 𝑞 будет меняться в зависимости от значения α𝑇 и σ𝐻.
Для трещины коэффициент 𝐷 определяется из условия равновесия в упругопластической области и вычисляется для плоской деформации по формуле:
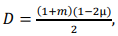 (7)
(7)
где 𝑚 — коэффициент степенного упрочнения; μ — коэффициент Пуассона в упругой области.
Данный коэффициент для феррито-перлитных сталей принимает значения от 0,22 до 0,26.
Множитель перед 𝐷 в формуле 𝑞 = 1 − 2𝐷/√3 для трещины составляет 1,156, а 𝑞 для феррито-перлитных сталей — 0,73. Действительно, при подстановке α𝑇 = 7,3 (6) при σ𝐻 = 0,2, получаем 𝑞 ≅ 0,73. Далее найдем α𝑇, если 0,2⁄σ𝐻 > 1, при котором реализуется такое же напряженное состояние, как при α𝑇 = 7,3 и 0,2⁄σ𝐻 → 1.
В [20] исследовано влияние α𝑇 на эффективный коэффициент концентрации напряжений 𝐾э, а для типичного алюминиевого сплава показано, что в диапазоне α𝑇 от 7 до 13 наблюдается глобальный экстремум значения 𝐾э. Вполне вероятно, что такое существенное максимальное значение может свидетельствовать о хрупком разрушении на начальных этапах циклического нагружения или несплошности в вершине концентратора. В данном случае ресурс будет зависеть только от дальнейшей способности материала препятствовать распространению макротрещины.
Модель критического состояния в вершине острого макроконцентратора напряжений. Практически все дефекты сварного соединения трубопроводов, корпусных судовых конструкций и др. создают концентрацию напряжений. В [9] представлена аналитическая модель, разработанная на базе понятия «локальный коэффициент концентрации напряжений». Кроме того, получена простая зависимость на основе формулы Нейбера, связывающей теоретический обобщенный коэффициент концентрации и коэффициенты концентрации интенсивности упругих напряжений и деформаций. В итоге для критической величины пластичности в очаге концентратора получена следующая зависимость:
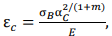 (8)
(8)
где α𝑐 — критическое значение теоретического коэффициента концентрации напряжений; σ𝐵 — условный предел прочности; 𝐸 — модуль упругости; 𝑚 — показатель степенного упрочнения.
Зависимость (8) дает такие высокие значения, которые редко встречаются на практике. Например, при критической логарифмической деформации для стали 50 критический коэффициент концентрации — 26, а для высокопрочной стали 37ХН3А с σ𝐵 = 1014 МПа — более 18. Можно заключить, что такая пластичность до нарушения сплошности в первых циклах нагружения недостижима. Это не удивительно, так как известно, что величина предельной пластичности для образцов с концентраторами напряжений существенно ниже, чем для образцов без концентрации напряжений. Кроме того, ε𝑐 должно определяться не только свойствами материала, но и условиями развития пластической деформации перед разрушением. Похожие результаты дает зависимость, используемая в [9]:
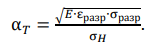 (9)
(9)
С. А. Куркин использовал ее для сравнительной оценки чувствительности материала к концентрации напряжений. Здесь α𝑇 характеризует концентратор, в котором трещина возникает при конкретной нагрузке σ𝐻. Далее будем использовать для этого случая понятие «наиболее вероятное зарождение макротрещины в концентраторе» (born crack) α𝑇𝑏𝑐. Истинные деформацию и напряжение в момент возникновения несплошности в вершине концентратора обозначим соответственно εразр и σразр. Их можно определять по общепринятым формулам εразр ≅ εкр = ln[ 1/(1− φк)] и σразр ≅ 𝑆отр = σв (1 + 1,4φк). Здесь 𝑆отр — истинные напряжения разрушения при одноосном напряженном состоянии. Учтем, что текучесть в концентраторе наступает согласно (5). Заменим σ𝐻 = 0,2 и 0,2 на σ∗0,2 . В итоге получим для критических состояний (α𝑇 = α𝑇𝑏𝑐) относительные напряжения зарождения разрушения σн𝑏𝑐/0,2 от концентратора:
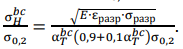 (10)
(10)
Отметим, что при очень малом радиусе вершины концентратора (ρ < 10𝑑𝑧, где 𝑑𝑧 — средний диаметр зерна) распространение трещины ограничивается при неизменном α𝑇. Как показано в [6], это зависит от 𝑑𝑧 стали. Формулы (8) и (9) привлекательны для инженера тем, что позволяют сравнивать чувствительность материалов к концентрации напряжений и использовать исходные данные механических характеристик стали.
Можно получить несколько иную модель, учитывающую СНС в области вершины макроконцентратора. Автор [12] использует силовой критерий хрупкого разрушения в материале конструкции σ1 > 𝑆отр, где 𝑆отр — напряжение нормального отрыва в приближении к одноосному напряженному состоянию. Важно, что данная характеристика материала не зависит от температуры его испытания. Используем этот критерий несколько иначе — для момента возникновения несплошности в области вершины концентратора напряжений. Полагаем, что 𝑆отр достижимо в случае постоянства энергетического равенства при СНС и одноосном напряженном состоянии, т. е. при потере пластической устойчивости и переходе от объемного напряженного состояния (когда σ𝑖 мало) к одноосному напряженному состоянию с неизбежным возрастанием деформаций.
Используем степенную аппроксимацию диаграммы деформирования в рамках деформационной теории пластичности. Приравняем истинные напряжения σ𝑖 диаграммы деформирования в функции упругого решения задачи σ𝑖 = 𝐹(σ𝑖(𝑦)) к 𝑆отр. В результате получим:
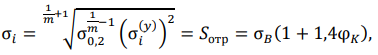 (11)
(11)
σ𝑖(𝑦)
где σ𝑖(𝑦) — одноосные напряжения при упругом решении задачи.
Записывая (11) относительно σ𝑖(𝑦), получим выражение для упругого решения задачи о концентрации напряжений с другой стороны: σ𝑖(𝑦) = α𝑇 ∙ σ𝐻. Таким образом:
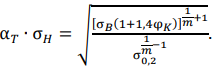 (12)
(12)
Здесь σ𝐻 — номинальная рабочая нагрузка на сварное соединение. В жестких точках сварных конструкций, соединений или при перегрузках она может достигать значения предела текучести материала. Представим частный случай в условиях циклического нагружения с упрочнением материала для момента образования несплошности born crack — зарождения разрушения. После преобразований (12) запишем упрощенную формулу:
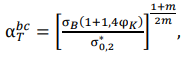 (13)
(13)
где α𝑇𝑏𝑐 — значение теоретического коэффициента концентрации напряжений, при котором происходит зарождение разрушения в области вершины макроконцентратора; 0,2 ∗ — предел текучести материала в вершине концентратора, который может повышаться согласно (5) в случае СНС.
В момент равенства α𝑇 = α𝑇𝑏𝑐 номинальные напряжения должны быть эквиваленты напряжениям зарождения (разрушения) σH𝑏𝑐. Для этой ситуации можно записать в относительных значениях σH𝑏𝑐⁄0,2 и построить зависимости относительных значений напряжений образования разрушения от теоретического коэффициента концентрации α𝑇𝑏𝑐 = α𝑇:
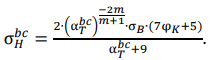 (14)
(14)
К сожалению, не представляется возможным записать (14) относительно α𝑇𝑏𝑐 при σH𝑏𝑐⁄0,2 = 1. Однако α𝑇𝑏𝑐можно найти численно для конкретной нагрузки σH𝑏𝑐 или построить диаграммы опасности возникновения несплошностей в виде макротрещины в очаге концентратора.
Аналитически получены зависимости для расчета критических теоретических коэффициентов концентрации напряжений, связанных с механическими характеристиками материала и заданной внешней статической нагрузкой при условии возникновения объемного напряженного состояния для концентраторов в сварных соединениях. Показано, что объемность напряженного состояния в очаге концентратора существенно влияет на величину критического теоретического коэффициента концентрации напряжений. Установлено, что сложное напряженное состояние в очаге концентратора может контролироваться геометрическими характеристиками самого концентратора и его расположением относительно внешнего поля напряжений.
Экспериментальные данные сталей (таблица 1) получены из литературных источников. Это ферритоперлитные материалы, для которых формула (14) показала хорошее согласование. Зависимость (14) привлекательна тем, что в качестве исходных данных используются стандартные механические характеристики. Ее также можно применить для оценки опасности дефектов в зоне сплавления (рис. 1,2), где образуются закалочные структуры, свойства которых значительно отличаются от исходных характеристик свариваемой стали.
Решения по (9) и (14) применяются чаще для самых хрупких сталей при невысоких σT𝑏𝑐. Однако в области высокой концентрации напряжений критические отношения σH𝑏𝑐⁄0,2 для разных сталей будут весьма близки по значениям. Это можно объяснить тем, что при СНС в области вершины для всех сталей создается напряженное состояние, подобное опасному случаю. В области же малых концентраций напряжений решения по модели (9) показывают более высокие критические значения напряжений σH𝑏𝑐. Отметим, что среднее значение σT𝑏𝑐 при σH𝑏𝑐 ≈ 0,2 составляет ~8,5. Для разных по механическим характеристикам сталей оно меняется не так значительно, как по расчетным результатам модели (9).
Рис. 5 построен для проверки результатов расчетов по физической адекватности модели (14). Это графики зависимостей критического состояния σH𝑏𝑐⁄0,2 от σT𝑏𝑐.
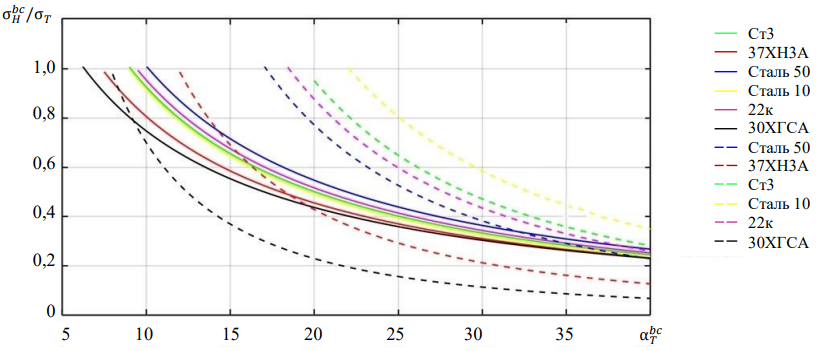
Рис. 5. Зависимости изменения относительного напряжения внешней нагрузки σH𝑏𝑐⁄0,2 от σT𝑏𝑐 для критического состояния в вершине концентратора напряжений. Сплошные кривые рассчитаны по формуле 14; пунктирные — формула (10)
Модель (9), не учитывающая объемность и повышение напряжений текучести в вершине концентратора, для стали 10 дает σT𝑏𝑐 = 91 при напряжениях σH𝑏𝑐 = 0,50,2, что маловероятно. Если учитывать объемность в этой модели, то σT𝑏𝑐 = 33, что существенно меньше. При учете объемности напряженного состояния критическая пластическая деформация снижается до возникновения разрушения при статическом растяжении образцов. Это подтвердили эксперименты с различными сталями и сплавами6. Более того, на корродированных образцах исследователи получали меньшую пластичность сталей. При этом было показано, что в вершинах создается объемное напряженное состояние, и объемность препятствует свободному протеканию пластичности. Пластичность до разрушения этих образцов составляла около 40 %, а предел текучести повышался до 27 % [21]. Можно заключить, что более глубокие концентраторы обусловливают большее повышение предела текучести.
Результаты косвенных опытов позволяют утверждать, что при гидростатической нагрузке текучесть не фиксируется, в этом случае материал разрушается только хрупко. Однако в очаге концентратора при увеличении внешней нагрузки объемное напряженное состояние не может оставаться достаточно стабильным для развития более высокого уровня объемности. Поэтому бифуркация неизбежна. Далее развитие может пойти по двум направлениям:
- хрупкое разрушение или его зачатки в очаге;
- потеря устойчивости напряженного состояния и, как следствие, переход к резкому возрастанию пластических деформаций.
Вероятно, момент бифуркации следует считать критическим состоянием в очаге концентратора. Возможно, этот момент значительно зависит от глубины концентратора, его относительной длины и глубины к толщине детали, ориентации к внешнему полю напряжений, а также от механических характеристик и протяженности очага концентратора. Все это требует дополнительных исследований и более точных решений.
Обсуждение и заключения. Дефекты и конструктивные особенности сварных соединений (форма разделки кромок, непроплавление, подрезы, поры, закалочные структуры и др.) снижают статическую и усталостную прочность. Для сварных соединений типичны концентраторы напряжений, имеющие длинную и неглубокую форму по отношению к толщине соединяемых деталей (подрезы) или длинную и глубокую (непроплавления и др.). Все они снижают усталостную прочность. Аналитические модели, полученные в представленной работе, позволяют сделать ряд заключений.
1. Работа материала при высоких значениях теоретического коэффициента концентрации напряжений зависит от напряженного состояния и его жесткости, а также от механических и структурных характеристик. Последние могут отличаться от параметров исходного материала, так как вершины концентраторов могут находиться в зонах сплавления сварных соединений.
2. Жесткое напряженное состояние в очаге концентратора напряжений может привести к повышению предела текучести. В этом случае прохождение сдвиговой деформации сдерживается, а наступление предельного состояния достигается при меньшем значении теоретического коэффициента концентрации напряжений и характеризуется несплошностью при постоянном значении внешней нагрузки.
3. Сравнение высокопрочных сталей с пластичными и сталями обычной прочности при одном и том же уровне σH𝑏𝑐⁄0,2 дает следующие результаты. Во втором случае образование объемности напряженного состояния будет более существенно сказываться на изменении критического значения теоретического коэффициента концентрации напряжений, при котором происходит зарождение разрушения в области вершины макроконцентратора σT𝑏𝑐 (рис. 5).
4. Сравнение моделе (14) и (10) позволяет сделать определенный вывод. С учетом жесткости напряженного состояния и повышения предела текучести при σH𝑏𝑐⁄0,2 → 1 снизу (10) дает оценку σT𝑏𝑐 с запасом по прочности, если речь идет о σH𝑏𝑐⁄0,2 = 0,8 (30ХГСА). Для менее прочной стали (14) запас по прочности при σH𝑏𝑐⁄0,2 = 0,5 (37ХН3А) и т. д. Таким образом, предпочтительнее учитывать объемность и использовать модель (14).
5. Зависимости на диаграмме теоретических коэффициентов напряжений более плотно сгруппированы в (14), чем в (10) из-за очень похожих напряженных состояний в области вершин острых концентраторов напряжений. Поэтому механические характеристики сталей оказывают второстепенное влияние на σT𝑏𝑐.
6. При увеличении теоретического коэффициента концентрации напряжений и уменьшении σT𝑏𝑐 при одном уровне σH𝑏𝑐⁄0,2 внешней нагрузки снижается влияние структурного фактора в стали на возникновение начального разрушения (образование несплошности). Однако для дальнейшего разрушения существенное значение будет иметь сопротивляемость материала росту макротрещины. После ее возникновения срабатывают другие критерии механики и кинетики разрушения.
Представленное исследование может служить предпосылкой к разработке аналитических моделей для оценки остаточного ресурса сварных соединений и конструкций, подверженных действию циклических нагрузок. Дальнейшие изыскания, предположительно, уточнят аналитические модели. Авторы проверят и апробируют результаты путем моделирования средствами CAE и перейдут к оценке эффективных коэффициентов концентрации напряжений.
1. Сергеев Н.Н., Сергеев А.Н. Механические свойства и внутреннее трение высокопрочных сталей в коррозионных средах. М., Вологда, 2020. 431 с.
2. Молоков К.А., Новиков В.В., Турмов Г.П. Основы расчетного проектирования сварных конструкций. Владивосток, 2019. Т. 1. 204 с.
3. Молоков К. А. Оценка поврежденности феррито-перлитных сталей в условиях малоциклового нагружения. В: Наука. Инновации. Техника и технологии: проблемы, достижения и перспективы : сб. тр. конф. Комсомольск-на-Амуре; 2015. С 125-128 URL: https://elibrary.ru/item.asp?id=23752241&selid=46181945 (дата обращения: 31.10.2022).
4 Молоков К. А. Оценка поврежденности феррито-перлитных сталей в условиях малоциклового нагружения.
5. Сергеев Н. Н., Сергеев А. Н. Механические свойства и внутреннее трение высокопрочных сталей в коррозионных средах.
6. Кроха В.А. Упрочнение металлов при холодной пластической деформации. Москва; 1980. 157 с.
Список литературы
1. Молоков К.А., Новиков В.В., Турмов Г.П. и др. Оценка надежности судовых конструкций с микротрещинами и остаточными сварочными напряжениями. Морские интеллектуальные технологии. 2018;1(3):45–54.
2. Новиков В.В., Турмов Г.П., Суров О.Э. и др. Повреждения и расчетный анализ прочности корабельных конструкций. Владивосток: Дальневосточный федеральный университет; 2020. 266 с.
3. Ерофеев В.В., Игнатьев А.Г., Олейник Н.И. и др. Математическая модель для оценки коэффициентов концентрации напряжений в сварных тавровых соединениях. Информационные технологии. Проблемы и решения. 2021;(4):28–36.
4. Молоков К.А., Сахарова А.В., Михалев М.В. Оценка пределов выносливости сварных соединений по критерию распространяющихся трещин. Вестник Инженерной школы Дальневосточного федерального университета. 2017;30(1):42–51. https://doi.org/10.5281/zenodo.399005
5. Казанов Г.Т., Новиков В.В., Турмов Г.П. Концентрация напряжений и другие особенности напряженного состояния судовых корпусных конструкций. Владивосток: Дальневосточный федеральный университет; 2014. 178 с.
6. Молоков К.А., Новиков В.В., Турмов Г.П. и др. Математические модели оценки эксплуатационного ресурса и работоспособности судовых сварных конструкций. Владивосток: Дальневосточный федеральный университет; 2021. 240 с.
7. Емельянов О.В., Шаповалов Э.Л., Гаврилов В.Б. Уровень концентрации упругих напряжений в стыковых сварных соединениях в зависимости от конструктивных. БСТ: Бюллетень строительной техники. 2017;11:26–28.
8. Махутов Н.А., Албагачиев А.Ю., Алексеевна С.И. и др. Прочность, ресурс, живучесть и безопасность машин. Москва: Либроком; 2008. 576 с.
9. Ямалеев К.М., Гумерова Л.Р. Структурные аспекты разрушения металла нефтепроводов. Уфа: Гилем; 2011. 144. с.
10. Хажинский Г.М. Деформирование. Разрушение. Надежность: Задачи деформирования и разрушения стали. Методы оценки прочности энергетического оборудования и трубопроводов. Москва: Ленанд; 2014. 544 с.
11. Ларионов В.П., Филиппов В.В. Хладостойкость материалов и элементов конструкций: результаты и перспективы. Новосибирск: Наука; 2005. 290 с.
12. Крыжевич Г.Б. Методы расчета предельной и усталостной прочности конструкций морской техники в низкотемпературных условиях. Труды Крыловского государственного научного центра. 2019;2:41–54. http://doi.org/10.24937/2542-2324-2019-2-388-41-54
13. Смирнов А.Н., Муравьев В.В., Абабков Н.В. Разрушение и диагностика металлов. Москва: Инновационное машиностроение; 2016. 479 с.
14. Негода Е.Н. Усталость сварных соединений труб большого диаметра. Вестник инженерной школы Дальневосточного федерального университета. 2015;4:62–74.
15. Матохин Г.В., Горбачев К.П. Инженеру о сопротивлении материалов разрушению. Владивосток: Дальнаука; 2010. 281. с.
16. Митенков Ф.М., Волков И.А., Игумнов Л.А. и др. Прикладная теория пластичности. Москва: Физматлит; 2015. 284 с.
17. Левин В.А., Вершинин А.В. Нелинейная вычислительная механика прочности. Т. 2. Численные методы. Москва: Физматлит; 2015. 544 c.
18. Матвиенко Ю.Г. Двухпараметрическая механика разрушения. Москва: Физматлит; 2021. 208 с.
19. Панферов В.М. Концентрация напряжений при упругопластических деформациях. Известия академии наук СССР. Отделение технических наук. Механика и машиностроение. 1954;(4):47–65.
20. Бьюи Х.Д. Механика разрушения: обратные задачи и решения. Москва: Физмалит; 2011. 412 с.
21. Петрова Н.Е., Баева Л.С. Биокоррозия корпусов судов. Вестник МГТУ. Труды Мурманского государственного технического университета. 2006;9(5):890–892.
Об авторах
К. А. МолоковРоссия
Молоков Константин Александрович, доцент Департамента промышленной безопасности, Политехнический институт, доцент кафедры «Информационные технологии и системы», кандидат технических наук
690091, г. Владивосток, ул. Суханова, 8
690014, РФ, г. Владивосток, ул. Гоголя, 41
В. В. Новиков
Россия
Новиков Валерий Васильевич, доцент Департамента морской техники и транспорта, кандидат технических наук
690091, Владивосток, ул. Суханова, 8
М. Дабалез
Россия
Дабалез Мохаммад, магистрант Департамента промышленной безопасности, Политехнический институт
690091, Владивосток, ул. Суханова, 8
Рецензия
Для цитирования:
Молоков К.А., Новиков В.В., Дабалез М. Оценка появления начальных разрушений от концентраторов напряжений в сварных соединениях и элементах конструкций. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):41-54. https://doi.org/10.23947/2687-1653-2023-23-1-41-54
For citation:
Molokov K.А., Novikov V.V., Dabalez M. Evaluation of the Occurrence of Initial Failures from Stress Concentrators in Welded Joints and Structural Elements. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):41-54. https://doi.org/10.23947/2687-1653-2023-23-1-41-54












































