Scroll to:
Mathematical Model of the pH Control System in an In Vitro Model of the Gastrointestinal Tract of Poultry
https://doi.org/10.23947/2687-1653-2023-23-1-95-106
Abstract
Introduction. Essential nonlinearity of the chemical reactions of acids and bases determines the control algorithms in the mode of acidification or alkalization, that is, periodic dosing of a minimum volume of acid or alkali. Such regulation may be ineffective, specifically, it allows insufficient or excessive concentration of the controlled substance. The article discusses the problem of precise regulation of the hydrogen index in mini-bioreactors. It is proposed to use a digital model of the acidity control system to select the concentrations of topped-up solutions, determine the regulation methodology, and improve accuracy. The objective of the work is the assurance of required accuracy of pH regulation in an in vitro mini-model of the gastrointestinal tract of a static type.
Materials and Methods. The initial block diagram of the model included accumulators and flows. It was the base for the main differential equations characterizing the change in volume and acidity. To correct the acidity readings of the resulting solution by temperature, a static model based on the polynomial approximation of experimental data using the least squares method was created. The structural elements of the mathematical model were investigated in the Matlab Simulink application package. To validate the adequacy of the mathematical model, transient characteristics were determined on a real system of in vitro modeling of the artificial gastrointestinal tract of poultry.
Results. Within the framework of this work, the authors created and analyzed a nonlinear mathematical model of pH changes in a bioreactor taking into account external control actions. The flows of hydrochloric acid solution, alkali solution and drain from the reactor were presented as elements of a differential equation describing the accumulation of liquid in the reactor. To improve the accuracy, the solution was modified taking into account the temperature dependence of the hydrogen index. A dosing mathematical model based on a regulator with alkali and acid channels was proposed. The data obtained made it possible to generate a combined model of the pH regulation process in the bioreactor. The adequacy of the solution was confirmed empirically. The models of pH regulator, regulation of the volume of contents in the reactor and chemical reactions were shown in the form of structural diagrams. The transients of a mathematical model and a real control system were compared. It was established that the transient characteristics of the mathematical model and the real system were identical in terms of regulation time. The relative error of regulation of the real system was 0.35 %, and the mathematical model — 0.1 %, which corresponded to the required accuracy of regulation ± 0.1 pH. The influence of the studied flows on the neutralization reaction was shown in the form of graphs.
Discussion and Conclusions. The proposed mathematical model will provide selecting optimal methods and algorithms for regulating acidity, which will accelerate the creation of a regulator for the nonlinear process of regulating the hydrogen index. In the future, these developments can be integrated into a comprehensive digital model of the entire artificial gastrointestinal tract of poultry to optimize control algorithms (dosing, mixing, periodicity, etc.), as well as approximation to objects in vivo.
Keywords
For citations:
Donskoy D.Yu., Lukyanov A.D., Filipović V., Asten T.B. Mathematical Model of the pH Control System in an In Vitro Model of the Gastrointestinal Tract of Poultry. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):95-106. https://doi.org/10.23947/2687-1653-2023-23-1-95-106
Introduction. Since the early 1980s, the scientific community studying the physiology and functional features of human internal organs has come to understand that in the near future, the focus of experimental techniques will shift from “in vivo” practices to “in vitro” systems [1]. The development of systems for hardware simulation of physiological processes will be of primary relevance, including for the following reasons: reduction of costs and time for conducting research; possibility of simultaneous conducting of the same type of experiments; and, what is not unimportant – increasing the ethics of research, reducing the need for experiments on living beings. By the beginning of the XXI century, a whole scientific direction was formed, engaged in the development of techniques and equipment for “in vitro” modeling and research [1].
Currently, in vitro models of the gastrointestinal tract are divided into two classes: static and dynamic. Static installations allow you to simulate the processes of digestion when using liquid nutrient media [2]. Dynamic models, unlike static ones, allow modeling peristaltic movements in the gastrointestinal tract, and are used when working with content nutrient media.
From the point of view of the simulated volume, the gastrointestinal tract models (regardless of the previous classification) are divided into micro- (up to 50 ml), mini- (from 50 to 400 ml) and macro-systems (over 400 ml) [3]. Microfluidic systems should be mentioned separately [4], but they go far beyond the scope of this work.
Patent analysis makes it possible to determine that the first is a patent for an invention “In vitro model of an in vivo digestive tract”1. This system is dynamic and precedes the market entry of the first TIM-2-type systems [5]. The development of this approach occurred in the models DGM [6], TIM-2 [5], HGS [7], etc. Static models, such as: DIDGI [8], SIMGI [9], SHIME [10], ARCOL [11], etc., moved away from complex modeling of peristalsis, and focused on more accurate modeling of the actual digestive processes. One of the reasons for this is the technical complexity and high cost of implementing systems with dynamic content compression. Another reason was the development of mathematical modeling methods and microcontroller control systems, which made it possible to control the medium in a test tube (reactor) with high accuracy and stability [4].
In this paper, we consider the solution to a particular problem of mathematical modeling of the pH regulation process for an in vitro mini-model of the gastrointestinal tract (gastrointestinal tract) of a static type [12]. The importance of precise control of the acidity of the chyme is determined by rather strict requirements for the conditions of in vitro experiments. Ensuring plausible conditions for the course of digestive processes, as well as the requirements for repeatability of experiments, require automatic pH control in the bioreactor with an accuracy not worse than ±0.1 units.2 At the same time, the pH range can be from slightly alkaline (7.9 pH, oral cavity) up to strongly acidic (1.3 pH, stomach).
The objective of this work is to ensure the required accuracy of pH adjustment in an in vitro mini-model of the gastrointestinal tract (gastrointestinal tract) of a static type.
To achieve this goal, the following tasks will be solved in the work:
- development of mathematical model of nonlinear pH change in a bioreactor taking into account external control actions;
- study of a mathematical model by simulation methods;
- refinement of the mathematical model in order to increase its accuracy by taking into account the temperature dependence of the hydrogen index;
- development of a mathematical model of the dosing process based on a two-channel competitive regulator (via alkali and acid channels);
- development of a unified mathematical model of the pH regulation process in a bioreactor;
- conducting experimental studies to confirm the adequacy of the combined mathematical model and determine the achieved accuracy of regulation.
Materials and Methods. To simulate the neutralization reaction, we will use the method of accumulators and flows [13]. The method is based on the use of fundamental or local conservation laws (accumulators) and mathematical description of patterns that change the amount of accumulated feature (flows).
The block diagram of the model is described in the figure, and contains two drives:
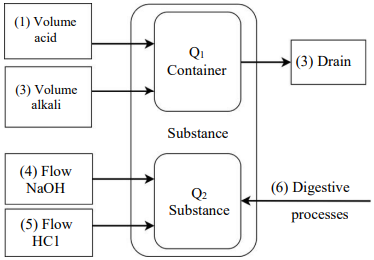
Fig. 1. Block diagram of the model
The reactor as a physical object simultaneously acts as a storage of the amount of liquid (Q1) and a storage of the amount of hydrogen ions (Q2). This is a container in which a controlled digestion process takes place, accompanied by a change in pH and a change in fluid volume.
There are three threads acting on the first drive:
- the first stream is the volume of acid topped up;
- the second stream is the volume of added alkali;
- the third stream is the volume poured out of the reactor.
The second drive is also affected by three threads:
- the fourth flow is the supply of sodium hydroxide by a pump [2];
- the fifth stream is the intake of hydrochloric acid. [2];
- the sixth stream is a potential change in pH during digestion. However, from a methodological point of view, it is a disturbing effect, and is not discussed in this paper.
Now, let us consider the mathematical implementation of the model for describing physico-chemical processes.
The volume of liquid in the reactor is described by the following equation:
V = S * h. (1)
Therefore, the change in the volume of liquid in the reactor:
dV = S * dh. (2)
For convenience, let us call the streams:
- the hydrochloric acid solution flow: q1=G1;
- the flow of the alkali solution (sodium hydroxide): q2= G2;
- the discharge flow of the solution from the reactor: q2 = G3.
Thus, the differential equation describing the accumulation of liquid in the reactor:
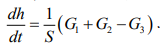 (3)
(3)
To determine the dynamics of changes in the concentration of the solution in the reactor, it is required to find the differential of the amount of substance according to the following formula:
v = V * C, (4)
where V is the volume of the substance, l; C is the molar concentration, mol/l.
From (4) and (1), we obtain:
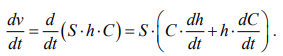 (5)
(5)
The change in the concentration of the solution is influenced by the flows of alkali and acid with a certain concentration, then:
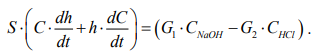 (6)
(6)
From equality (6), we express the change in concentration and simplify the expression:
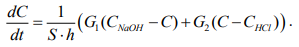 (7)
(7)
Thus, the system of differential equations describing the dynamics of changes in the volume and concentration of the solution in the bioreactor is presented in formula 8:
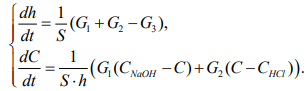 (8)
(8)
To obtain the concentration of H ([H+]) cations from the solution of the system of equations (8), let us recall the basics of chemistry. The concentrations of hydrogen ions ([H+]) and hydroxide ions ([OH-]) in distilled water at 25 °C are equal and amount to 10-7 mol/l, this directly follows from the definition of the ionic product of water, which is presented below [11]:
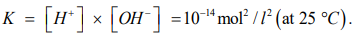 (9)
(9)
It is also worth considering that:
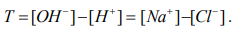 (10)
(10)
Now we find [H+] (denoted as CH) through the square root of the previous expressions, taking into account the concentration of the solution according to equation (4) of our mathematical model [14]:
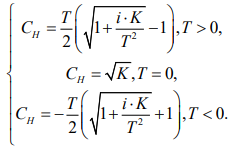 (11)
(11)
Where ions i = 4.
To create a control system with feedback on acidity in the form of a hydrogen index (pH), it is necessary to calculate a negative decimal logarithm from the concentration calculated according to equations (7). Thus, we get the acidity of the solution under normal conditions, that is, at 25 ℃.
But the contents of the bioreactor are not always in normal conditions. For example, to create an artificial environment characteristic of the in vivo environment of the gastrointestinal tract of poultry, a temperature of 42℃ is maintained in the reactor3. Therefore, experimentally and on the basis of available research4 a matrix of changes in the pH of buffer solutions depending on temperature was obtained on high-precision pH meters, and the readings were obtained using a measuring system with thermal compensation for the electrode used5 [13].
Based on these data, a static model was constructed, it was obtained by polynomial approximation by the least squares method. A visual representation of the pH dependence on temperature is shown in Figure 2: [14–16].
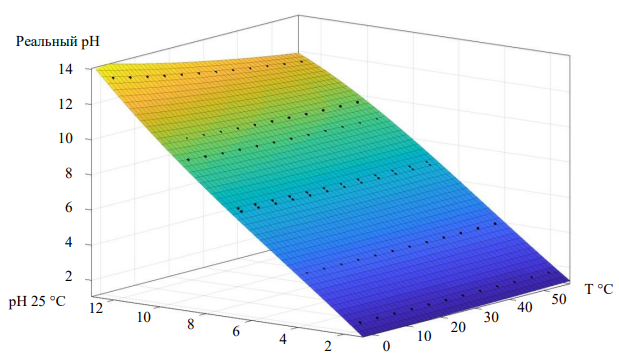
Fig. 2. A surface describing the dependence of pH on temperature (12)
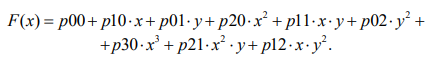 (12)
(12)
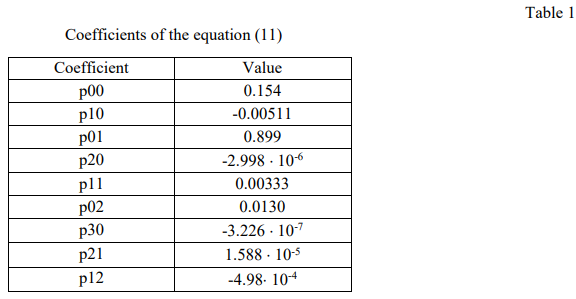
The coefficients of the equation are presented in Table 1.
To determine the transients in the system, we will build a mathematical model in the MATLAB Simulink application package (Fig. 3):
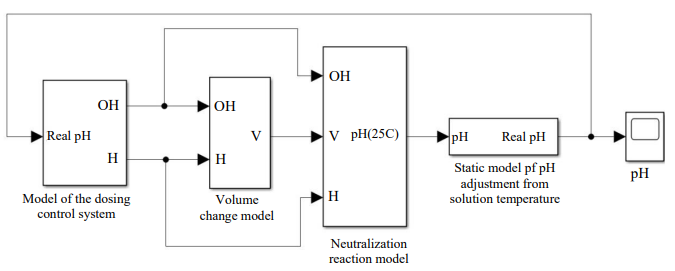
Fig. 3. General structure of the mathematical model in MATLAB Simulink
Let us consider the created system by blocks. The first block is a block of a two-channel acidity regulator with feedback. Noise has been introduced into the feedback circuit to simulate random events of a real system for measuring acidity and measuring instrument errors.
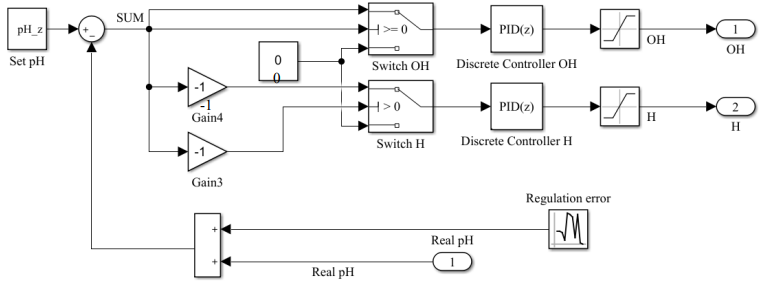
Fig. 4. Structure of the pH regulator, block “Model of the dosing control system”
The second unit is a system for monitoring the volume of solution in the reactor. The “Drain volume controller” function simulates the activation of pumping. If the volume of the solution approaches the maximum volume of the reactor, the function gradually resets the solution to the required volume.
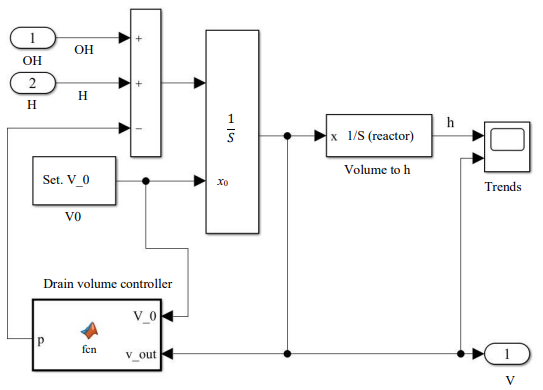
Fig. 5. Structure of the reactor content volume control model, block “Volume change model”
The third block is the main one. It implements the calculation of the chemical reaction of acid and alkali when added to the reactor and calculates the pH of the final solution under normal conditions. The function called “Neutralization” calculates the concentration of hydrogen ions in a solution [12]. And the “Concentration in pH” block implements the conversion of concentration into a hydrogen pH indicator.
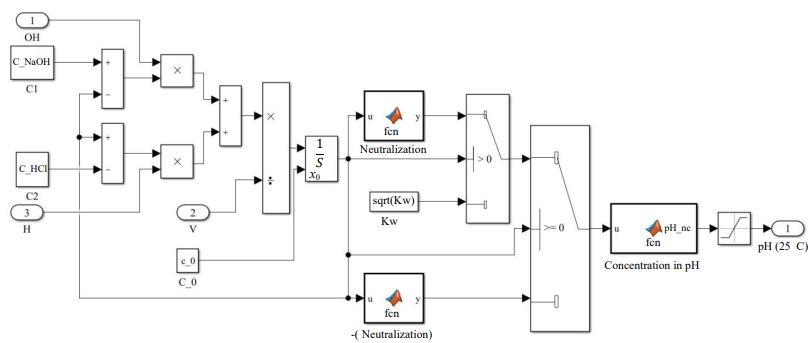
Fig. 6. Structure of the model describing the neutralization reaction
The fourth block enables to take into account the temperature changes of the solution with the function of the statistical model in the “Temperature correction” block.
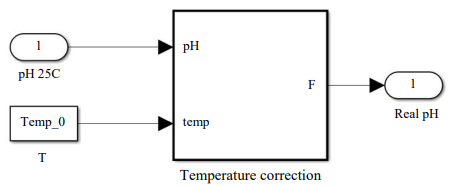
Fig. 7. Structure of the model describing the change in acidity from temperature, block “Static model of pH adjustment from solution temperature”
To determine the adequacy of the transient characteristics of the resulting mathematical model, experiments were conducted on a simulation model. The real model is represented by an automated control system for the artificial gastrointestinal tract of poultry with one control unit and a bioreactor. Figure 8 shows the experimental equipment and its description.

Fig. 8. Research equipment and its description: a — bioreactor environment control units; b — elements of bioreactor. 1 — controlled agitators; 2 — heaters; 3 — ports with sensors and a system for topping/draining solutions
The methodology of the experiment is as follows. The mathematical model takes into account the characteristics of a real system, such as:
- set acidity;
- reactor parameters (base area and height of the bioreactor);
- concentrations of added substances (acids and alkalis);
- initial concentration of the solution;
- initial volume of the solution;
- the temperature of the solution throughout the experiment;
- discreteness of the control process [14].
The mathematical model is an ideal system in which mixing of solutions in the reactor occurs instantly and uniformly. In real conditions, this is impossible, therefore, forced mixing is needed for the uniform dissolution of the added acid or alkali. In the simulation model, this problem is solved by a magnetic stirrer controlled via a SCADA system.
Unfortunately, this type of mixing device induces electromagnetic interference on the pH electrode. To eliminate interference, the mixing device was switched off for a short time, and the discreteness of measurements and the operation of the regulator was 20 seconds, which is due to the experimentally established time of normalization of the pH readings of the electrode in the reactor (according to the documentation of the electrode, sampling can reach 1-2 minutes).6 7 The regulator of the real system is limited in the maximum volume of the dosed acid or alkali in order to ensure safety, which was taken into account in the model regulator.
Experimental Results. Figure 10 shows a comparison of the transition process of a mathematical model and a real control system. The pH electrode is a sensitive element that is susceptible to receiving external electromagnetic interference.
One of the experiments was carried out at a given acidity of the solution in the range of 2.15 ± 0.05 pH. The acidity of the initial solution was 6.2 pH. The temperature of the solution in the reactor: 22.25 ℃. Solutions of 0.1 mol/liter NaOH and 0.1 mol/liter HCl were used to change the acidity. The dosing algorithm consisted in discrete proportional regulation.
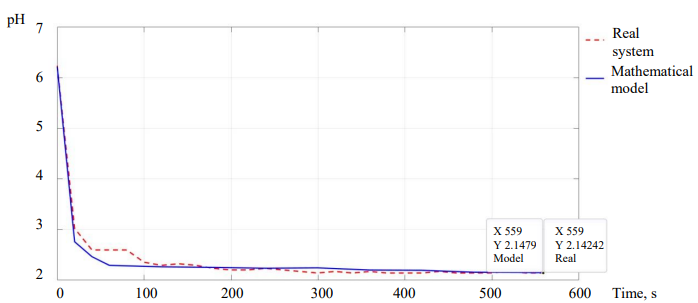
Fig. 8. Transient characteristics of a mathematical model and a real system when regulating from 6.2 to 2.15 pH
Figure 11 shows the flow integrals from differential equation (7).
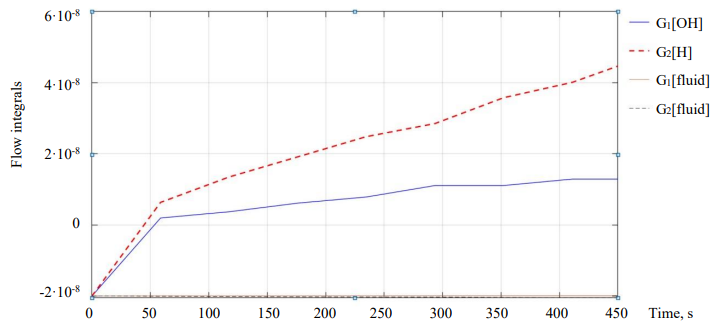
Fig. 9. The effect of each flow on the neutralization reaction during experiments
Discussion and Conclusions. Analysis of the simulation results have shown that flows with a solution concentration in the reactor do not make a significant contribution to the regulation of the entire system, therefore, they can be neglected for simplification. Then the system of differential equations of the digital model (8) will take the following form:
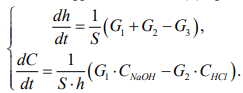 (13)
(13)
According to the results of the experiments, taking into account the concentration of the solution in the reactor, the relative error of the steady-state acidity of the solution for the mathematical model was 0.1 %, and for a real system with the same algorithm 0.35 %.
Thus, taking into account the error of the electrode readings and the neglect of the mixing process of solutions in the mathematical model, the absolute error of the control results is within acceptable limits and does not exceed ± 0.1 pH of the set value. This means that the developed mathematical model adequately describes the neutralization reaction curve, and in the future, it will allow choosing optimal control algorithms, which would be a laborious process on a real system.
The developed model solves the problem and is a mathematical tool for the development of methods and algorithms for pH regulation, taking into account the temperature of the contents of the mini-reactor, the initial concentration of the main solution and the concentrations of top-up solutions, which will improve existing control algorithms.
References
1. Verhoeckx K, Cotter P, Lopez-Exposito I, et al. (eds.) The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. 342 p. URL: https://www.ncbi.nlm.nih.gov/books/NBK500148/ (accessed: 28.09.2022).
2. Alegría A, Garcia-Llatas G, Cilla A. Static Digestion Models: General Introduction. In book: The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. P. 3–12. URL: https://link.springer.com/chapter/10.1007/978-3-319-16104-4_1 (accessed: 28.09.2022).
3. Dupont D, Alric M, Blanquet-Diot S, et al. Can Dynamic In Vitro Digestion Systems Mimic the Physiological Reality? Critical Reviews in Food Science and Nutrition. 2019;59:1546–1562. URL: https://doi.org/10.1080/10408398.2017.1421900 (accessed: 28.09.2022).
4. Steinway SN, Saleh J, Bon-Kyoung Koo, et al. Human Microphysiological Models of Intestinal Tissue and Gut Microbiome. Frontiers in Bioengineering and Biotechnology. 2020;8:725. URL: https://www.frontiersin.org/articles/10.3389/fbioe.2020.00725 (accessed: 28.09.2022).
5. Venema K. The TNO In Vitro Model of the Colon (TIM-2). In book: The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. P. 293–304. URL: https://link.springer.com/chapter/10.1007/978-3-319-16104-4_26 (accessed: 28.09.2022).
6. Mandalari G, Chessa S, Bisignano C, et al. The Effect of Sundried Raisins (Vitis vinifera L.) on the In Vitro Composition of the Gut Microbiota. Food & Function. 2016;7:4048–4060. URL: http://dx.doi.org/10.1039/C6FO01137C (accessed: 28.09.2022).
7. Ferrua M, Singh R. Human Gastric Simulator (Riddet Model). In book: The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. P. 61–71. 10.1007/978-3-319-16104-4_7
8. Ménard O, Picque D, Dupont D. The DIDGI®system. In book: The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. P. 73–81. 10.1007/978-3-319-16104-4_8
9. Barroso E, Cueva C, Peláez C, et al. The Computer-Controlled Multicompartmental Dynamic Model of the Gastrointestinal System SIMGI. In book: The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. P. 319–327. 10.1007/978-3-319-16104-4_28
10. Van de Wiele T, Van den Abbeele P, Ossieur W, et al. The Simulator of the Human Intestinal Microbial Ecosystem (SHIME®). In book: The Impact of Food Bioactives on Health. In Vitro and Ex Vivo Models. Cham, Heidelberg, New York, Dordrecht, London: Springer Open; 2015. P. 305–317. https://doi.org/10.1007/978-3-319-16104-4_27
11. González C, González D, Zúñiga RN, et al. Simulation of Human Small Intestinal Digestion of Starch Using an In Vitro System Based on a Dialysis Membrane Process. Foods. 2020;9(7):913. https://doi.org/10.3390/foods9070913
12. Donskoy D, Katin O, Alekseenko L. Development and Implementation of the GIT-Modelling Bioreactor System: The Way to Reducing a Carbon Footprint. E3S Web of Conferences. 2021;279:01030. https://doi.org/10.1051/e3sconf/202127901030
13. Asuero AG, Michałowski T. Comprehensive Formulation of Titration Curves for Complex AcidBase Systems and Its Analytical Implications. Critical Reviews in Analytical Chemistry. 2011;41:151–187. 10.1080/10408347.2011.559440
14. Garcia C, Juliani R. Modelling and Simulation of pH Neutralization Plant Including the Process Instrumentation. In book: Michalowski T (ed.). Applications of MATLAB in Science and Engineering. 2011. P. 485–510. http://dx.doi.org/10.5772/1534
15. Egger L, Ménard O, Abbühl L, et al. Higher Microbial Diversity in Raw than in Pasteurized Milk Raclette-Type Cheese Enhances Peptide and Metabolite Diversity after In Vitro Digestion. Food Chemistry. 2021;340:128154. https://doi.org/10.1016/j.foodchem.2020.128154
16. Chistyakov VA, Lukyanov AD, Donskoy DYu, et al. Modeling and Analysis of Energy Efficiency of Methods for Maintaining Temperature Conditions in Microbioreactors. IOP Conference Series: Materials Science and Engineering. 2020;900:012015. 10.1088/1757-899X/900/1/012015
About the Authors
D. Yu. DonskoyRussian Federation
Danila Yu Donskoy, postgraduate of the Production Automation Department
1, Gagarin sq., Rostov-on-Don, 344000
A. D. Lukyanov
Russian Federation
Alexandr D Lukyanov, Head of the Production Automation Department, Cand.Sci. (Eng.), associate professor
1, Gagarin sq., Rostov-on-Don, 344000
V. Filipović
Serbia
Vladimir Filipović, senior research fellow, Faculty of Technology
1, Bul. cara Lazara, Novi Sad, 21000
T. B. Asten
Russian Federation
Tamara B Asten, professor of the World Languages and Cultures Department, Dr.Sci. (Philology)
1, Gagarin sq., Rostov-on-Don, 344000
Review
For citations:
Donskoy D.Yu., Lukyanov A.D., Filipović V., Asten T.B. Mathematical Model of the pH Control System in an In Vitro Model of the Gastrointestinal Tract of Poultry. Advanced Engineering Research (Rostov-on-Don). 2023;23(1):95-106. https://doi.org/10.23947/2687-1653-2023-23-1-95-106












































