Перейти к:
Исследование динамических характеристик автоматизированного позиционного длинноходового пневмопривода технологического оборудования
https://doi.org/10.23947/2687-1653-2023-23-3-283-295
Аннотация
Введение. На длинноходовые перемещения в автоматизированных пневмоприводах приходится значительное количество исполнительных движений в координатных столах, на автоматизированных складах, раскройных машинах и т. д. Длинноходовые перемещения ухудшают динамическое качество и позиционирование привода. Это обусловлено трением поршня и нелинейными характеристиками потока сжатого газа в значительных объемах напорной и сливной полостей цилиндра. Таким образом, представляется перспективным создание автоматизированного позиционного пневмопривода для длинноходовых перемещений. Это позволит повысить производительность процессов при обеспечении заявленной точности.
Цель работы — получение математической модели и зависимостей основных параметров предложенного автоматизированного позиционного длинноходового пневмопривода технологического оборудования на участках разгона, движения с установившейся скоростью, замедления и торможения.
Материалы и методы. Базой для расчетов и моделирования стала схема двух траекторий перемещения из точки А в точку Е с учетом сил, затраченных на эти процессы. Оптимальное перемещение определили с помощью принципа Портнягина (то есть оптимального быстродействия). Пропорциональное управление приводом представлено как метод достижения результата. Для длинноходовых перемещений привода детально визуализированы (представлены как рисунки): схематическое решение и расчетная схема. Предложены оригинальный струйный датчик с внутренней пневматической связью и пневмомеханическое дискретнопропорциональное устройство для быстродействия контура управления. Математическая модель включает движение и торможение поршня, баланс массовых расходов, давление в точках и контур управления. Систему уравнений решали методом Рунге — Кутты в программном продукте «Симинтех» (Simintech). По итогам исследования обобщенной математической модели построили зависимости изменения кинематических, силовых и пневматических свойств привода в реальном времени при типовом цикле позиционирования. Информацию суммировали и представили как совокупность графиков.
Результаты исследования. Математическая модель сформирована по комплексу расчетов. Она учитывает зависимости, характерные для движения поршня пневмоцилиндра. Баланс массовых расходов исследуется по уравнениям расхода газа при сжатии в камере, через распределители и дроссели, в нагнетательной и сливной полостях и в управляющем устройстве. Рассмотрены неравенства, описывающие давления в точках и контур управления. Сложная математическая модель решалась в программной среде «Симинтех» (Simintech) методом Рунге — Кутты с изменяемым шагом интегрирования. Фрагмент работы программы выбран в качестве одной из иллюстраций. Он показывает, что софт задействует для расчетов такие показатели, как: заданная и приведенные координаты; универсальная газовая постоянная; коэффициенты жесткости пружины, сопротивления, адиабаты и вязкого трения в поршне; давление компрессора; массу подвижных частей пневмопривода; силу внешних сопротивлений; диаметры трубопровода, поршня пневмоцилиндра и тормозного устройства; протяженность хода поршня цилиндра; площади поршневых полостей и дросселей; длину трубопровода и его внутренний объем. Таким образом, программа оперирует значительным комплексом данных, что дает возможность получить существенные и адекватные результаты. Схематически показана взаимосвязь блоков и диаграмм, использованных при решении модели. Речь идет о графиках перемещений, площадей, давлений, скоростей и температур. Использованы блоки с текстом программы и предназначенные для интегрирования. Таким образом получены математическая модель автоматизированного пневмопривода технологического оборудования и зависимости основных параметров его работы. Графики свидетельствуют о том, что исполнительный механизм пневмопривода должным образом следует предложенной траектории.
Обсуждение и заключение. Итоги работы позволяют рассмотреть несколько этапов длинноходового перемещения привода, определить временные рамки этих процессов (от 0 до 0,65 сек), а также фиксируемые в данные промежутки изменения давления и скорости движения каретки пневмоцилиндра. Таких этапов пять: разгон, движение с установившейся скоростью, замедление, движение со скоростью позиционирования и торможение. Дальнейшие исследования будут сосредоточены на оптимизации системы для сокращения продолжительности и поддержания точного позиционирования при внешних воздействиях.
Ключевые слова
Для цитирования:
Коротыч Д.А., Сидоренко В.С., Приходько С.П. Исследование динамических характеристик автоматизированного позиционного длинноходового пневмопривода технологического оборудования. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):283-295. https://doi.org/10.23947/2687-1653-2023-23-3-283-295
For citation:
Korotych D.A., Sidorenko V.S., Prikhodko S.P. Investigation of Dynamic Characteristics of an Automated Position Long-Stroke Pneumatic Actuator of Fabrication System. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):283-295. https://doi.org/10.23947/2687-1653-2023-23-3-283-295
Введение. Производительность приводов определяется точностью позиционирования и скоростью перемещения координат в различных рабочих циклах. Современное промышленное оборудование часто оснащают автоматическими пневматическими приводами, для которых характерны длинноходовые перемещения. Это, например, портальное аппараты для контактной сварки, координатные столы и раскройные машины.
Современные позиционные пневмоприводы длинноходовых перемещений в технологическом оборудовании обеспечивают скорость до 30 мм/с и точность ~1 % от длины перемещения. В специальном исполнении при скорости до 100 мм/с точность позиционирования достигает 0,4 %. Отметим, что траектория движений формируется с помощью управления потоком сжатого воздуха в напорных или сливных трубопроводах и полостях пневмоцилиндра. В длинноходовых приводах длина таких полостей достигает 3 м. Сложные термодинамические процессы и сжимаемость в воздушных потоках — основные факторы, ограничивающие повышение точности [1–3].
Таким образом, необходимо увеличить производительность рабочих и технологических процессов оборудования при обеспечении заявленной точности. В данном случае представляется перспективным создание автоматизированного позиционного пневмопривода для длинноходовых перемещений. Новое решение должно учитывать такие характеристики пневмопривода, как скорость, массогабаритные показатели, пожаро- и взрывозащищенность [2][4].
Цель работы — получение математической модели и зависимостей основных параметров предложенного автоматизированного позиционного длинноходового пневмопривода технологического оборудования на участках разгона, движения с установившейся скоростью, замедления и торможения.
Материалы и методы. На рис. 1 схематически представлена транспортная задача перемещения из точки А в точку Е по двум траекториям. Учтены силы, затраченные на каждое из перемещений. Субоптимальное перемещение ABCDE (трапеция) при простом алгоритме управления реализуется за время 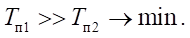 Оптимальное перемещение AFE (колокол) получено решением оптимального быстродействия на основе принципа Портнягина
Оптимальное перемещение AFE (колокол) получено решением оптимального быстродействия на основе принципа Портнягина 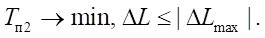 Результат достигается при более сложном пропорциональном управлении приводом. Траекторию движения обеспечивает точность переключения управлений движением по пути
Результат достигается при более сложном пропорциональном управлении приводом. Траекторию движения обеспечивает точность переключения управлений движением по пути 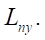
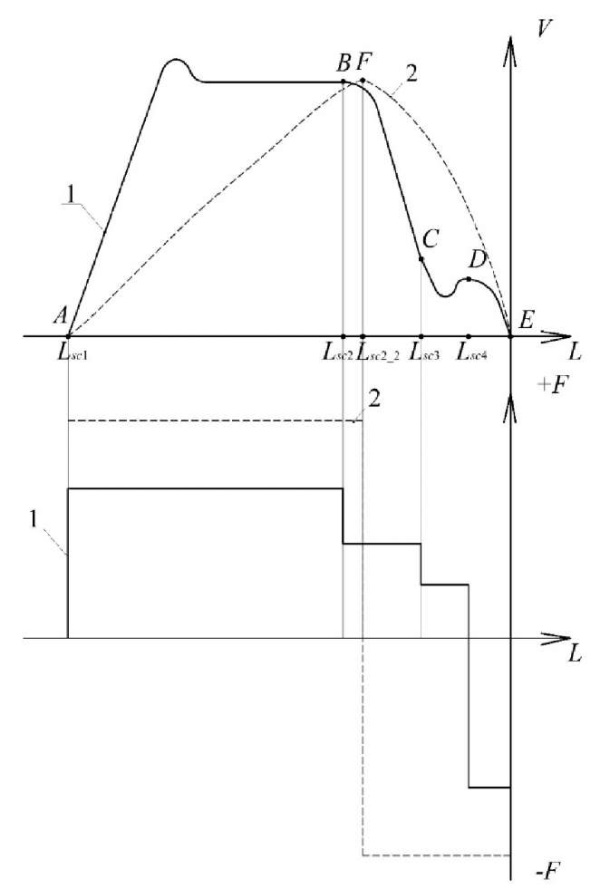
Рис. 1. Траектории перемещений:
1 — субоптимального ABCDE;
2 — оптимального AFE
В описании траектории 1 латинскими буквами обозначены точки переключения: А — на разгон привода; В — на замедление; С — на скорость позиционирования; D — на остановку. На участках AB и BC обеспечиваются начальный разгон и торможение до скорости позиционирования VПЗ и дальнейшей остановки тормозным устройством 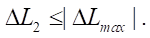
При движении по 2-й траектории: А — переключение на разгон привода; F — переключение на остановку.
При использовании траектории 1 увеличивается длительность перемещений, но меньше используются сила и мощность. Следовательно, точность будет лучше в сравнении с траекторией 2.
Предлагается оригинальный струйный датчик с внутренней пневматической связью и пневмомеханическое дискретно-пропорциональное устройство, позволяющее повысить быстродействие контура управления, так как обратные связи в известных аналогах при длинных ходах снижают точность основного двигателя примерно на 10–15 % [4–6].
Схематическое решение пневматического позиционного привода для длинноходовых перемещений показано на рис. 2. Привод работает в соответствии с субоптимальной траекторией движения, определяемой в задаче оптимальной скорости при заданной точности позиционирования. Здесь ПЦ1 — бесштоковый пневмоцилиндр длинноходовых перемещений, который осуществляет главное движение; ПЦ2, ПЦ3 — тормозные пневмоцилиндры, которые фиксируют привод; СА — струйный датчик, определяющий координату перемещения, ускорение привода, его скорость и усилие; Р1 — пневматический распределитель с электропневматическим управлением, он управляет подачей на струйный датчик; Р2 — главный управляющий распределитель; Р3 — распределитель с пневматическим управлением, он управляет работой тормозных пневмоцилиндров; Г1–Г4 — глушители, отвечающие за сброс давления в атмосферу; ДД — датчик давления, получающий данные со струйного датчика; ПЛК — логический контроллер; ШД — шаговый двигатель, управляющий золотником распределителя; БПВ — блок подготовки воздуха; ДР1, ДР2 — дроссель с обратным клапаном, служащий для регулирования скорости бесштокового пневмоцилиндра длинноходовых перемещений главного движения [7].
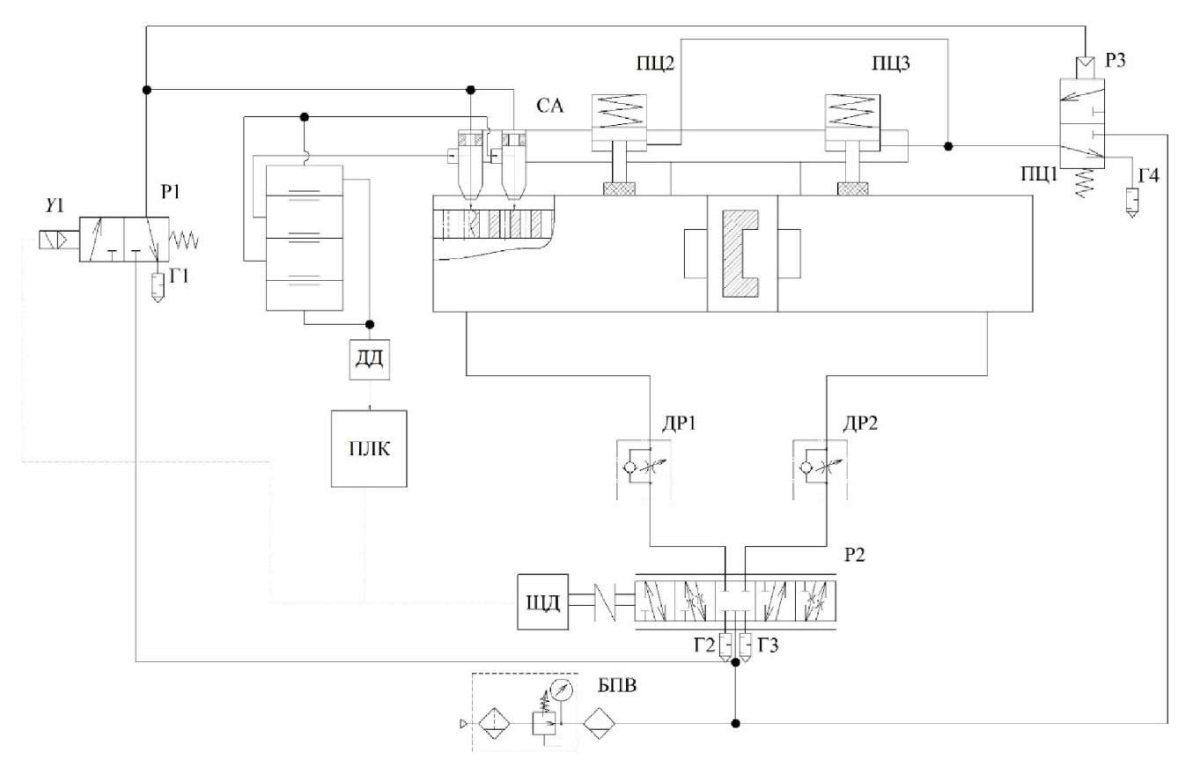
Рис. 2. Схемотехническое предложение автоматизированного позиционного длинноходового пневмопривода
Привод содержит систему управления, которая отслеживает положение каретки бесштокового пневмоцилиндра, замедляет ход при приближении к заданным координатам и посылает сигнал на тормозное устройство [1][4][7].
Быстродействие повышается введением дискретно-пропорционального регулирующего устройства. Для управления используются сигналы, формируемые контуром управления. Устройство выполнено в виде двух сопел и содержит компенсационные измерения.
Результаты исследования. Расчетная схема пневмопривода длинноходовых перемещений представлена на рис. 3. Здесь ПЦ1 — бесштоковый пневмоцилиндр длинноходовых координатных перемещений, осуществляющий главное движение; ПЦ2, ПЦ3 — тормозные пневмоцилиндры, фиксирующие привод во время остановки в нужном положении; СА — струйный датчик, определяющий координату перемещения, ускорение привода, его скорость и усилие; Р1 — пневматический распределитель с электропневматическим управлением, он управляет подачей на струйный датчик; Р2 — главный управляющий распределитель; Р3 — распределитель с пневматическим управлением, он управляет работой тормозных пневмоцилиндров; Г1–Г4 — глушители, отвечающие за сброс давления в атмосферу; ДР1–ДР2 — дроссель с обратным клапаном, служащий для регулирования скорости бесштокового пневмоцилиндра длинноходовых перемещений главного движения; ДД — датчик давления, получающий данные со струйного датчика; S — площадь поршня бесштокового пневмоцилиндра длинноходовых координатных перемещений; P1–Р5 — исследуемые давления в точках 1–5; Т1–Т5 — исследуемые температуры в точках 1–5; Fтр — сила трения в бесштоковом пневмоцилиндре длинноходовых перемещений; Fвт — сила вязкого трения в бесштоковом пневмоцилиндре длинноходовых перемещений; Fвн — внешняя сила в бесштоковом пневмоцилиндре длинноходовых перемещений; x — перемещение каретки бесштокового пневмоцилиндра длинноходовых перемещений; V — скорость перемещения каретки бесштокового пневмоцилиндра длинноходовых перемещений [7]; Cпр — жесткость пружины тормозных пневмоцилиндров; m — перемещаемая масса; Рт — давление в тормозных цилиндрах;
Ру — давление в управляющем канале; f1–f4 — площади проходных сечений; Ра — давление атмосферы; dз1–dз3 — диаметры золотников распределителей; Спрр1–Спрр3 — жесткость пружины распределителей 1–3; xp1–xp4 — перемещение золотников распределителей 1–4; Vp1–Vp4 — скорость перемещения золотников распределителей 1–4; Fэм1–Fэм2 — сила электромагнита управления распределителями 1–2; Pm — давление компрессора; Tm — температура, создаваемая компрессором.
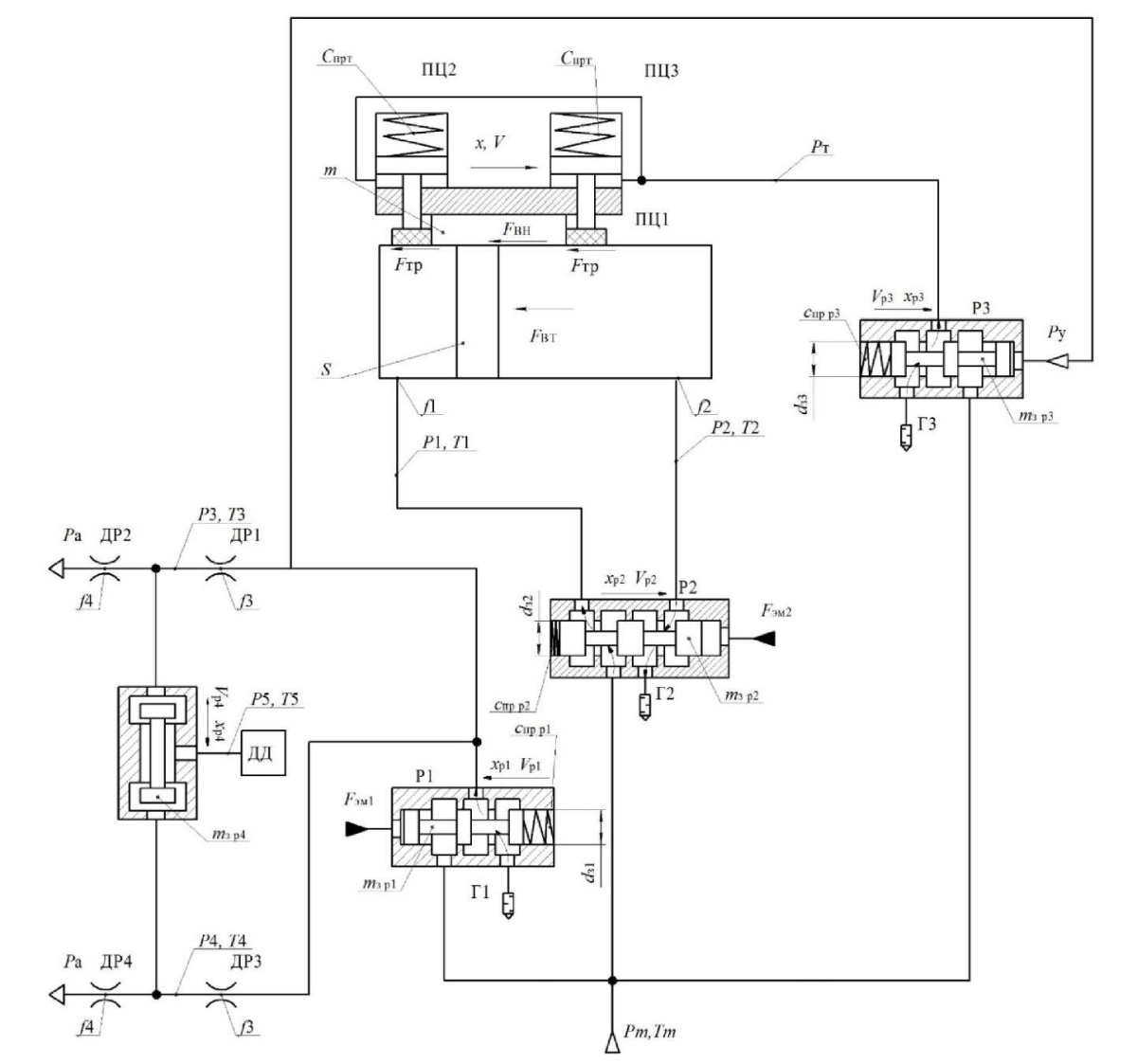
Рис. 3. Схема автоматизированного пневмопривода длинноходовых перемещений технологического оборудования
Математическая модель сформирована со следующими допущениями [8–12]:
- давление источника сжатого воздуха остается постоянным с течением времени;
- термодинамический процесс поведения газа в пневматической системе является адиабатическим;
- в описании пневматических устройств используется модель идеального газа, поскольку давление пневматической системы не превышает 10 бар;
- утечки не учитываются;
- сила вязкого трения пропорциональна скорости;
- коэффициент расходов экспериментально выявлен путем идентификации;
- масса перемещаемой детали постоянна;
- усилие на выходном звене пневмопривода постоянно.
1. Уравнение движения поршня пневмоцилиндра [1][4]:
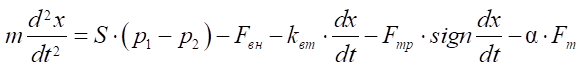 . (1)
. (1)
Здесь S — площадь поршня нагнетательной и сливной полостей бесштокового пневмоцилиндра длинноходовых координатных перемещений главного движения, м²;
P1, P2— давление воздуха в нагнетательной и сливной полостях цилиндра длинноходовых перемещений, Па;
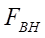 — внешние силы, Н;
— внешние силы, Н;
kвт — коэффициент вязкого трения;
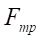 — сила трения, Н;
— сила трения, Н;
α — Булев параметр: α=0 при 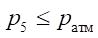 и α = 1 при
и α = 1 при 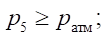
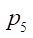 — давление в канале управления, Па;
— давление в канале управления, Па;
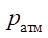 — давление атмосферы, Па [12–14];
— давление атмосферы, Па [12–14];
m — масса подвижных частей привода, кг;
FТ — сила торможения, Н.
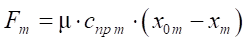 , (2)
, (2)
где cпр т — коэффициент жесткости пружины пневмоцилиндра тормоза;
μ — коэффициент трения.
2. Уравнение движения поршня пневмоцилиндра торможения:
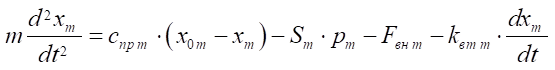 . (3)
. (3)
Здесь cпр т — коэффициент жесткости пружины пневмоцилиндра тормоза;
х0т — координата начального сжатия;
ST — эффективная площадь поршня сливной полости пневмоцилиндра тормоза, м²;
PM — давление воздуха соответственно в нагнетательной полости пневмоцилиндра тормоза, Па;
FВН Т — внешние силы, Н;
kвт т — коэффициент вязкого трения.
3. Уравнения баланса массовых расходов:
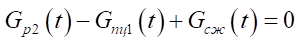 , (4)
, (4)
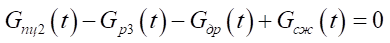 , (5)
, (5)
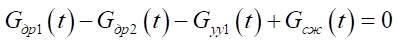 , (6)
, (6)
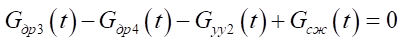 , (7)
, (7)
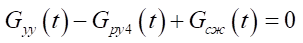 . (8)
. (8)
Здесь
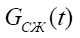 — массовый расход газа при сжатии в камере;
— массовый расход газа при сжатии в камере;
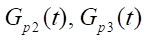 — массовый расход через распределители;
— массовый расход через распределители;
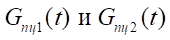 массовый расход в нагнетательной и сливной полостях бесштокового пневмоцилиндра длинноходовых перемещений;
массовый расход в нагнетательной и сливной полостях бесштокового пневмоцилиндра длинноходовых перемещений;
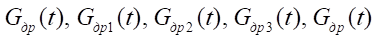 ,
, 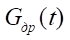 — массовый расход через дроссели в сливной линии, на входе в сопловой аппарат струйного датчика и на выходе из соплового аппарата;
— массовый расход через дроссели в сливной линии, на входе в сопловой аппарат струйного датчика и на выходе из соплового аппарата;
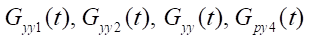 — массовый расход в каналах управления управляющего устройства, на выходе из управляющего устройства, распределителя тормозных пневмоцилиндров [7].
— массовый расход в каналах управления управляющего устройства, на выходе из управляющего устройства, распределителя тормозных пневмоцилиндров [7].
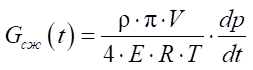 , (9)
, (9)
где
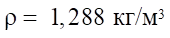 — плотность воздуха;
— плотность воздуха;
V — объем полости;
R = 287 Дж/(кг·К) — газовая постоянная;
E — объемный модуль упругости воздуха;
T — температура в точке;
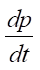 — изменение давления в точке [6].
— изменение давления в точке [6].
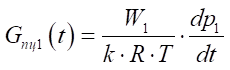 , (10)
, (10)
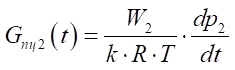 , (11)
, (11)
где W1 и W2 — текущие объемы в напорной и сливной полостях основного пневмоцилиндра, м³;
k — показатель адиабаты (для воздуха k = 1,4).
4. Уравнения давления в точках:
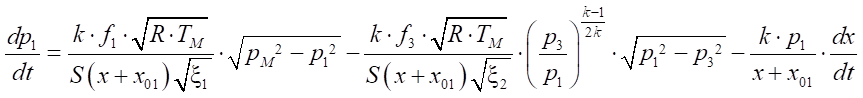 , (12)
, (12)
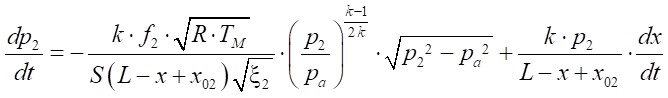 , (13)
, (13)
 , (14)
, (14)
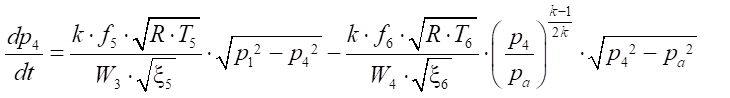 , (15)
, (15)
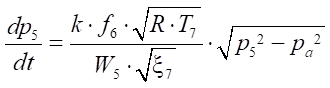 . (16)
. (16)
Здесь k — показатель адиабаты;
R — газовая постоянная, Дж/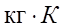 ;
;
TМ — температура воздуха в магистрали, К;
Pa — давление атмосферы, Па;
P1 - P5 — давления в проточных частях трубопровода, Па;
W1 - W5 — объемы проточных частей, м³;
x1 - x7 — коэффициенты сопротивления в линии;
f1 - f6 — площади проходных сечений трубопровода, м²;
L — максимальный ход поршня, м;
x01, x02 — отношение начальных объемов пневмопривода к полезной площади поршня поршневой полости пневмоцилиндра, м;
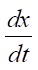 — скорость перемещения поршня, м/с.
— скорость перемещения поршня, м/с.
5. Уравнения контура управления.
Уравнение движения золотника распределителя 1:
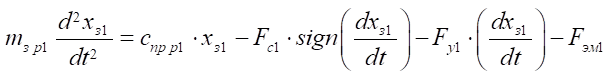 . (17)
. (17)
Уравнение движения золотника распределителя 2:
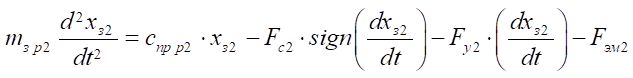 . (18)
. (18)
Уравнение движения золотника распределителя 3:
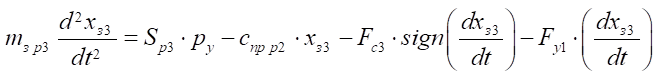 . (19)
. (19)
Уравнение движения золотника распределителя 4:
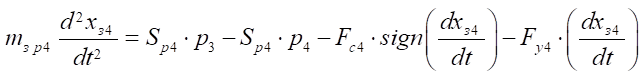 . (20)
. (20)
Здесь Sp — площадь торца золотника распределителя, м²;
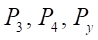 — давление в каналах управления, Па;
— давление в каналах управления, Па;
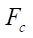 — силы сопротивления перемещению золотника распределителя, Н;
— силы сопротивления перемещению золотника распределителя, Н;
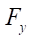 — силы реакции упоров, Н;
— силы реакции упоров, Н;
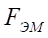 — сила электромагнита, действующая на золотник распределителя, Н;
— сила электромагнита, действующая на золотник распределителя, Н;
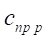 — коэффициент сжатия пружины, Н/м;
— коэффициент сжатия пружины, Н/м;
 — масса золотника распределителя, кг.
— масса золотника распределителя, кг.
Для решения математической модели использовали программный продукт «Симинтех» (Simintech). Задействовали метод Рунге — Кутты с изменяемым шагом интегрирования (рис. 4–5).
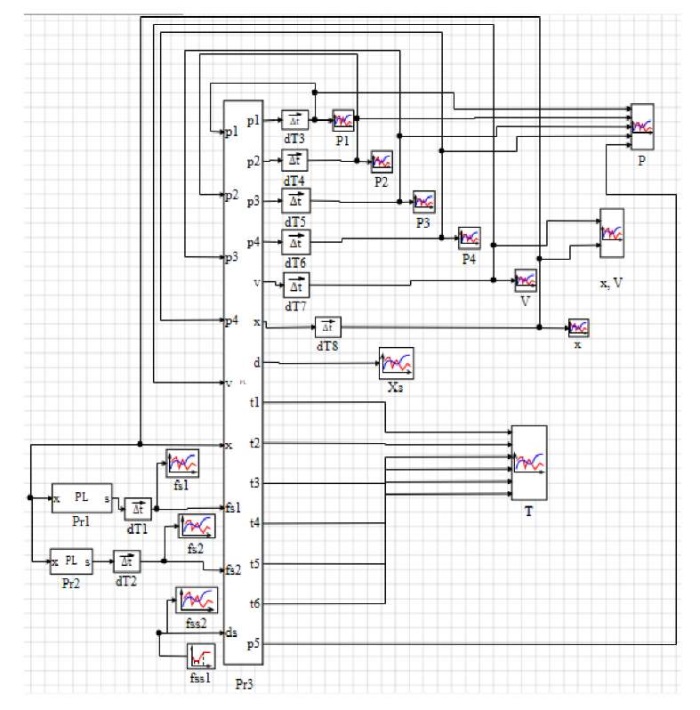
Рис. 4. Фрагмент модели в программе «Симинтех»
Здесь
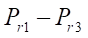 — блоки с текстом программы;
— блоки с текстом программы;
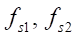 — графики вывода площадей 1 и 2 дросселя струйного датчика;
— графики вывода площадей 1 и 2 дросселя струйного датчика;
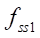 — блок задачи площадей проходных сечений струйного датчика;
— блок задачи площадей проходных сечений струйного датчика;
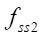 — графики вывода площадей проходных сечений струйного датчика;
— графики вывода площадей проходных сечений струйного датчика;
dT1–dT8 — блоки интегрирования;
Р1–Р4 — графики вывода полученных давлений в точках 1–4;
Р — общий график вывода всех давлений;
V — график вывода полученной скорости перемещения каретки бесштокового пневмоцилиндра;
х — график вывода полученного перемещения каретки бесштокового пневмоцилиндра;
х, V — общий график вывода полученного перемещения и скорости каретки бесштокового пневмоцилиндра;
Т — графики вывода полученных температур;
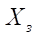 — график вывода полученного перемещения золотника управляющего распределителя.
— график вывода полученного перемещения золотника управляющего распределителя.
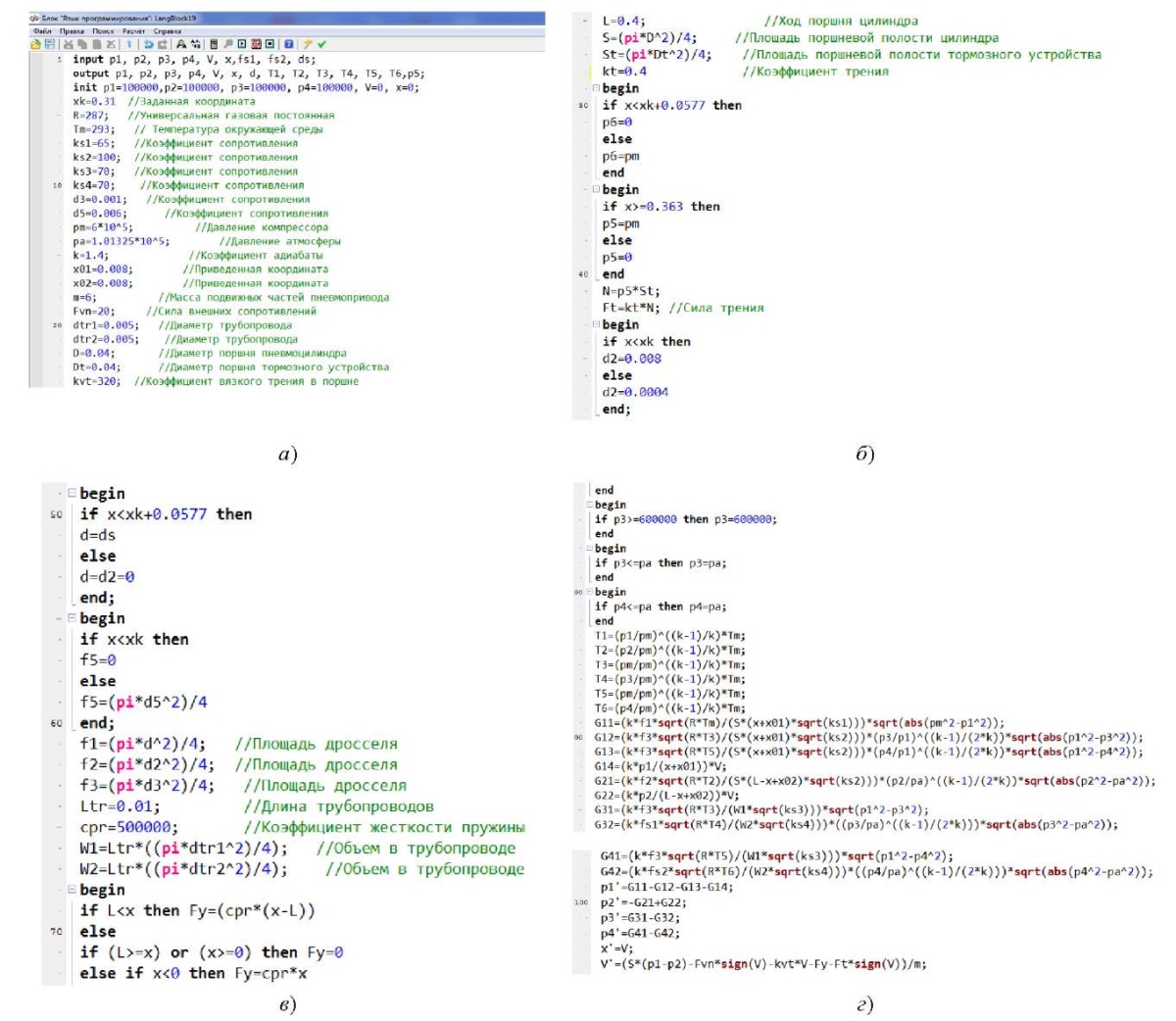
Рис. 5. Блок программирования в «Симинтех»:
а — часть исходных данных;
б — часть логических функций;
в — часть присваивания переменных;
г — основная часть программы
Исследование обобщенной математической модели предлагаемого привода позволило получить графики поведения привода при разгоне, замедлении и остановке (рис. 6), описывающие изменения кинематических, силовых и пневматических свойств привода в реальном времени при типовом цикле позиционирования [15].
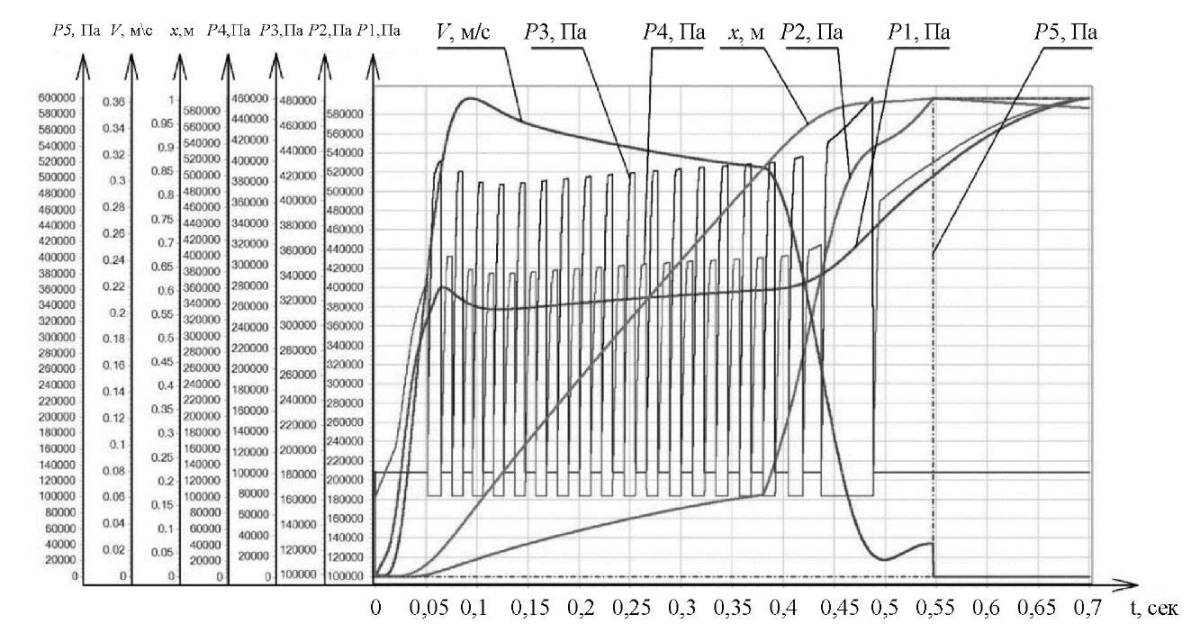
Рис. 6. Комплекс графиков по данным обобщенной математической модели
Обсуждение и заключение. График показывает длинноходовое перемещение по траектории, предложенной на рис. 1. Работа привода состоит из нескольких этапов.
- 0–0,1 сек. Разгон. Давление в напорной полости повышается до 4 бар, скорость движения каретки пневмоцилиндра — 1 м/с.
- 0,1–0,38 сек. Движение с установившейся скоростью. Давление в напорной полости — около 3,8 бар. Давление в сливной линии повышается до 1,6 бар, скорость движения каретки пневмоцилиндра — 0,85 м/с.
- 0,38–0,5 сек. Замедление. Давление в напорной и сливной полостях увеличивается. Скорость движения каретки пневмоцилиндра понижается до 0,075 м/с.
- 0,5–0,65 сек. Движение со скоростью позиционирования. Давление в напорной и сливной полостях повышается, скорость движения каретки пневмоцилиндра — 0,075 м/с.
- 0,65 сек. Переключение на торможение, активация внешнего тормозного устройства.
Полученные графики подтверждают, что длинноходовые перемещения пневмопривода выполняются в соответствии с предложенной траекторией (рис. 1) и система управления функционирует должным образом. Дальнейшие исследования будут сосредоточены на оптимизации системы для сокращения продолжительности и поддержания точного позиционирования при внешних воздействиях.
Список литературы
1. Коротыч Д.А., Сидоренко В.С. Позиционная система управления длинноходовыми пневмоприводами. В: Мат-лы XXIII междунар. науч.-тех. конф. студентов и аспирантов, посвященной 100-летию доктора технических наук, заслуженного профессора МЭИ, почетного академика водохозяйственных наук Бориса Тихоновича Емцева «Гидравлические машины, гидроприводы и гидропневмоавтоматика». Москва: Издательство «Мир науки»; 2019. С. 157–163. URL: https://www.elibrary.ru/item.asp?id=41599329 (дата обращения: 04.05.2023).
2. Jihong Wang, Gordon T. Energy Optimal Control of Servo-Pneumatic Cylinders through Nonlinear Static Feedback Linearization. Journal of Dynamic Systems, Measurement, and Control. 2012;134(5):051005. https://doi.org/10.1115/1.4006084
3. Дао Тхе Ань. Позиционный пневмопривод повышенного быстродействия и точности. Дис. канд. тех. наук. Ростов-на-Дону; 2016. 206 c. URL: https://viewer.rsl.ru/ru/rsl01008559478 (дата обращения: 04.05.2023).
4. Sidorenko V.S., Korotych D.A., Grishenko V.I., Kharchenko AN. Simulation of Pneumatic Actuator Position System for Long Stroke Mounting Movements. IOP Conference Series: Materials Science and Engineering. 2021;1029:012039. https://doi.org/10.1088/1757-899X/1029/1/012039
5. Галлямов Ш.Р., Стариков К.В., Целищев В.А. Экспериментальное исследование характеристик пневмопривода FESTO с пропорциональным распределителем расхода. Вестник Уфимского государственного авиационного технического университета. 2011;15(1)(41):26–33. URL: http://journal.ugatu.su/index.php/Vestnik/article/view/900 (дата обращения: 04.05.2023).
6. Mosadegh B., Polygerinos P., Keplinger Ch., Wennstedt S., Shepherd R.F., Gupta U., et al. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Advanced Functional Materials. 2014;24(15):2163–2170. https://doi.org/10.1002/adfm.201303288
7. Дао Тхе Ань, Сидоренко В.С. Моделирование процессов позиционирования быстродействующего пневмопривода робота. Фундаментальные исследования. 2015;(7–2):285–292. URL: https://fundamental-research.ru/ru/article/view?id=38687 (дата обращения: 06.05.2023).
8. Долгов Г.А. Комбинированный пневмопривод поворотно-делительных механизмов повышенного быстродействия и точности. В: Мат-лы XXIII междунар. науч.-тех. конф. студентов и аспирантов, посвященной 100-летию доктора технических наук, заслуженного профессора МЭИ, почетного академика водохозяйственных наук Бориса Тихоновича Емцева «Гидравлические машины, гидроприводы и гидропневмоавтоматика». Москва: Изд-во «Мир науки»; 2019. С. 119–126.
9. Lemeshko M., Molev M., Golovin I. Hydraulic Technological Machines with Adaptive Drive Structure. MATEC Web of Conferences. 2018;224:02087. https://doi.org/10.1051/matecconf/201822402087
10. Дао Тхе Ань, Сидоренко В.С., Дымочкин Д.Д. Исследование точности позиционирования автоматизированного пневмопривода с внешним тормозным устройством. Вестник Донского государственного технического университета. 2015;15(4):46–53. https://doi.org/10.12737/16077
11. Gorin A., Tokmakov N., Kyznetsov I. Substantiation of Parameters of Machine with Volumetric Hydraulic Drive for Formation of Wells in Ground. In: Proc. 5th International Conference on Industrial Engineering (ICIE). Cham: Springer; 2019. P. 1315–1323. URL: https://link.springer.com/chapter/10.1007/978-3-030-22063-1_139 (дата обращения: 04.05.2023).
12. Vardhan A., Dasgupta K., Mishra S.K. Dynamic Analysis of a Closed-Circuit Hydraulic Drive System Used in the Rotary Head of Blasthole Drilling Machine Using MATLAB-Simulink Environment. In: Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. 2019;233(6):702–719. https://doi.org/10.1177/0959651818808870
13. Obukhova E.N., Grishchenko V.I., Dolgov G.A. Formalization of Dynamic Model of Pneumatic Drive with Variable Structure. MATEC Web of Conferences. 2018;226:02022. https://doi.org/10.1051/matecconf/201822602022
14. Seppe Terryn, Joost Brancart, Dirk Lefeber, Guy Van Assche, Bram Vanderborght. Self-Healing Soft Pneumatic Robots. Science Robotics. 2017;2(9):4268. https://www.science.org/doi/10.1126/scirobotics.aan4268
15. Obukhova E.N., Popov A.N. Synergetic Synthesis of Nonlinear Adaptive Control for Pneumatic Drives. In: Proc. IV Int. Conf. on Control in Technical Systems (CTS). New York: IEEE; 2021. https://doi.org/10.1109/CTS53513.2021.9562786
Об авторах
Д. А. КоротычRussian Federation
Даниил Андреевич Коротыч, ассистент и аспирант кафедры гидравлики, гидропневмоавтоматики и тепловых процессов
344003, г. Ростов-на-Дону, пл. Гагарина, 1
В. С. Сидоренко
Russian Federation
Валентин Сергеевич Сидоренко, доктор технических наук, профессор кафедры гидравлики, гидропневмоавтоматики и тепловых процессов
344003, г. Ростов-на-Дону, пл. Гагарина, 1
С. П. Приходько
Russian Federation
Сергей Павлович Приходько, ассистент и аспирант кафедры гидравлики, гидропневмоавтоматики и тепловых процессов
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Рецензия
Для цитирования:
Коротыч Д.А., Сидоренко В.С., Приходько С.П. Исследование динамических характеристик автоматизированного позиционного длинноходового пневмопривода технологического оборудования. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):283-295. https://doi.org/10.23947/2687-1653-2023-23-3-283-295
For citation:
Korotych D.A., Sidorenko V.S., Prikhodko S.P. Investigation of Dynamic Characteristics of an Automated Position Long-Stroke Pneumatic Actuator of Fabrication System. Advanced Engineering Research (Rostov-on-Don). 2023;23(3):283-295. https://doi.org/10.23947/2687-1653-2023-23-3-283-295
JATS XML














































