Scroll to:
Software Control of the Movement of a Differential Drive Robot for Different Friction Models
https://doi.org/10.23947/2687-1653-2023-23-4-346-355
EDN: INDAIS
Abstract
Introduction. Designing motion control systems for mobile robots requires the construction of mathematical models. Researchers have repeatedly addressed this topic. In particular, works have been published on the calculations of multiphysical processes, modeling the movement of various types of wheels under certain conditions. In addition, the dynamics of deformable contacting bodies during sliding, rolling and rotation, issues of autonomy and controllability of mobile robots were considered. Note, however, that the dynamics and positioning accuracy of wheeled robots is largely determined by friction. The literature does not present studies on the dynamics of a robot with a differential drive taking into account the interrelationships of sliding, spinning and rolling friction effects based on the theory of multicomponent friction. Research in this area can reveal new dynamic effects. Based on the data obtained in this way, it is possible to improve the accuracy of positioning in building mathematical control models. The presented work aims at investigating the movement of an automatic device with a differential drive taking into account three contact models: nonholonomic, Coulomb friction, and multicomponent models.
Materials and Methods. The scheme of a two-wheeled robot with differential drive and continuous movement on the support surface was adopted as the basic one. The movement of the device was provided through software control. The dynamics was described in the form of Appel equations. Mathematical models were used for calculations, taking into account friction in different ways. Coordination of the actions of the mechanism was formed at a dynamic level. The control actions were the moments of the wheel motors. When visualizing the models under study, the built-in numerical methods of the Wolfram Mathematica system were used with a minimum accuracy of 10-6.
Results. When building a mathematical model, the equations for the angular velocities of the wheels were determined. The authors took into account the presence of a contact site and derived the equations of dynamics of a differential drive robot. The elements of the system were force and moment projections, indicators of platform spin, masses, angular accelerations, and inertia of the wheels. It was shown how control actions were formed within the framework of nonholonomic mechanics. The model of engines that created a moment of control on the driving wheels was described. The solution was derived as the relationship between the inductance of the conductors of electric motors and the operation of the power supply. Three models describing the dynamics of a differential drive robot were examined in detail. The first model was nonholonomic. The second and third included a system of equations for the dynamics of a differential drive robot for a general case with a contact platform. At the same time, in the second model, the switching time in the engine was ignored and the Coulomb friction was involved. In the third model, a parameter to determine the speed of transients in the engine was introduced, and Pade decomposition was involved. This was a model with multicomponent friction. The calculation results were shown in the form of graphs. On them, the studied models were visualized in the form of curves of different colors. Comparison of the graphs showed in which cases, after the completion of transients, the control provided the required accuracy. These were models 1 and 2. In model 3, the software control generated an error in the angular velocity of rotation of the platform. This error could not be predicted within the framework of the 1st and 2nd models. In all the systems considered, the sliding speed of the wheels in the transverse direction dropped to zero. The condition of continuous motion of the support wheel was obtained and validated.
Discussion and Conclusion. Software control is acceptable in models that do not take into account wheel friction during simultaneous sliding, spinning and rolling (general case of spatial motion). However, it is important to consider the relationship between these processes and multicomponent friction. This is required for the robot to perform program movements more accurately. It was established that software control in a model that takes into account the friction of spinning and rolling caused deviations from the program values of the angular velocity of the platform. The results obtained can be used in the building of a control system with predictive models.
Keywords
For citations:
Salimov M.S., Merkuryev I.V. Software Control of the Movement of a Differential Drive Robot for Different Friction Models. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):346-355. https://doi.org/10.23947/2687-1653-2023-23-4-346-355. EDN: INDAIS
Introduction. In the modern world, the demand for automatic mobile wheeled vehicles is growing, and the possibilities of coordinating their operation are being actively explored. Issues of autonomy and controllability of mobile robots are of considerable scientific and applied interest. In particular, approaches to the calculations of multiphysical processes, simulating the movement of specific types of wheels under different conditions are considered. Some studies focus on the dynamics of deformable contacting bodies during sliding, rolling and rotation. The results of these studies are used in robotics [1-3]. The control of mobile wheeled vehicles is considered on the example of electric scooters “Segway” [4].
Mobile mechanisms with simple and efficient wheel motion control systems are needed primarily for operating in narrow spaces [5], for conducting research under difficult industrial conditions [6].
In [7-11], the possibilities of accurate modeling of the dynamics of wheeled vehicles are shown, taking into account the sliding, spinning, and rolling of the wheels.
At the same time, the phenomena arising from the combination of friction effects are not described in the literature. The presented work aims at investigating the effect of multicomponent friction on the dynamics of a robot with a differential drive. Tasks involve building a mathematical model of robot movement with multicomponent friction and simulating program movements.
Materials and Methods. The scheme of a two-wheeled differential drive robot is considered (Fig. 1). The continuous movement of wheels of radius R along the support surface is assumed.
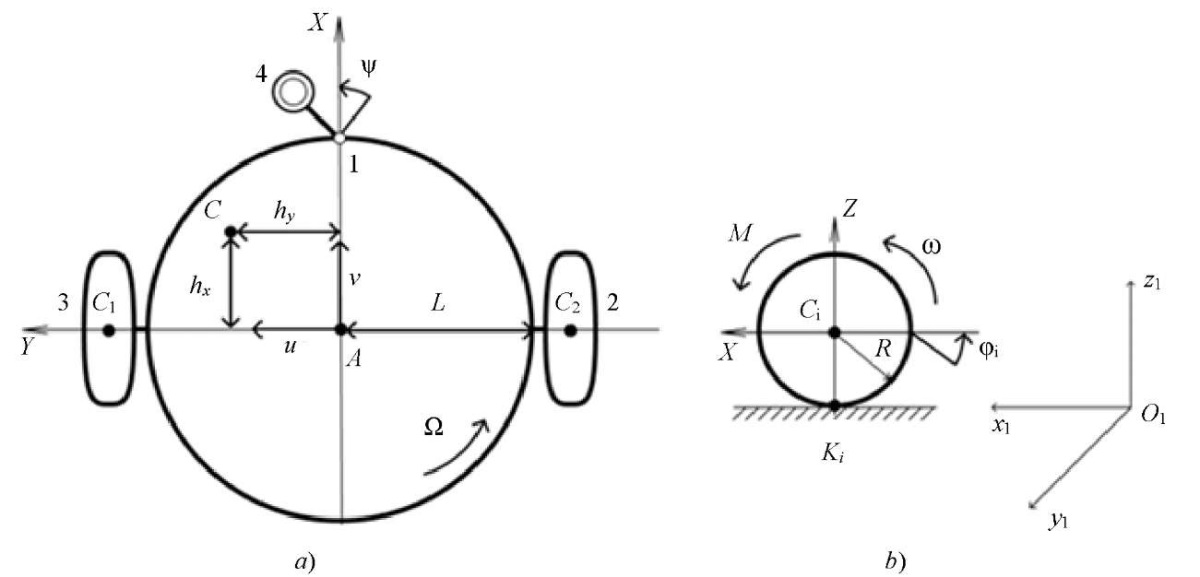
Fig. 1. Kinematic diagram of the robot:
a — platform; b — one of the driving wheels
The gravity center of platform C is shifted relative to the geometric center of platform A along X axis by distance 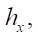 along Y — axis — by distance
along Y — axis — by distance 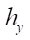 . Points
. Points 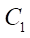 and
and 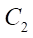 — centers of mass of the wheels (index 1 corresponds to the left wheel, index 2 —to the right).
— centers of mass of the wheels (index 1 corresponds to the left wheel, index 2 —to the right).
The following designations are introduced:
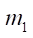 — mass of the robot platform;
— mass of the robot platform;
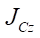 — moment of inertia of the platform relative to the center of mass C;
— moment of inertia of the platform relative to the center of mass C;
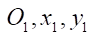 — fixed coordinate system;
— fixed coordinate system; 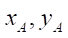 determine the position of point A in
determine the position of point A in 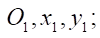
y — angle of the course of the platform;
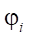 — wheel steering angles (index 1 corresponds to the left wheel, index 2 — to the right);
— wheel steering angles (index 1 corresponds to the left wheel, index 2 — to the right);
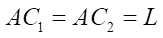 — wheels width;
— wheels width;
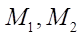 — engine torques applied to the wheels.
— engine torques applied to the wheels.
It is assumed that only the normal bearing reaction acts on the support wheel 4 (Fig. 1). On the move, the support wheel is located on X axis at a distance 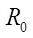 from the center of the platform
from the center of the platform 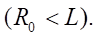
Research Results
Mathematical model of robot dynamics. When describing the movement of a differential drive robot in the framework of nonholonomic mechanics, expressions are used that take into account the limitations associated with zero wheel slip relative to the surface:
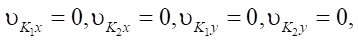 (1)
(1)
where 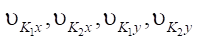 — projections on Х and Y axes of velocities of points
— projections on Х and Y axes of velocities of points 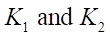 , which are centers of the contact areas of the wheels and the supporting surface.
, which are centers of the contact areas of the wheels and the supporting surface.
Note that for a nonholonomic model, a point contact of the wheels and the surface is assumed, i.e., the contact area of each wheel degenerates into a single point of contact.
Consider the expressions:
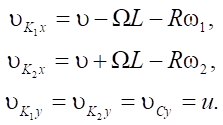 (2)
(2)
With their help, equality for the angular velocities of the wheels can be obtained:
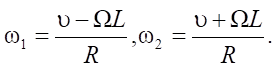 (3)
(3)
In the general case, when the presence of a contact platform is assumed, we obtain the equations of dynamics of a differential drive robot:
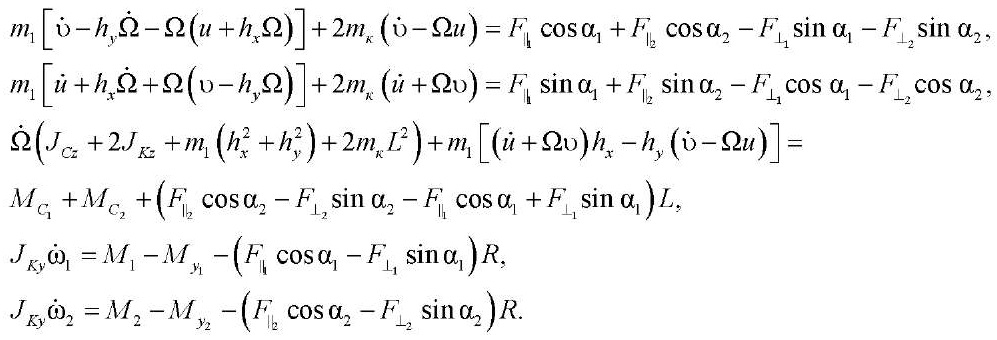 (4)
(4)
Here,
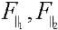 — projections of the friction force on the directions of the slip speeds of the centers of the wheel contact patches;
— projections of the friction force on the directions of the slip speeds of the centers of the wheel contact patches;
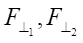 — projections of the friction force in directions perpendicular to the speeds of the centers of the wheel contact patches;
— projections of the friction force in directions perpendicular to the speeds of the centers of the wheel contact patches;
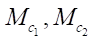 — summands of the friction torque under spinning for two wheels;
— summands of the friction torque under spinning for two wheels;
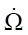 — angular acceleration of platform spinning;
— angular acceleration of platform spinning;
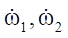 — angular accelerations of wheels projected onto their axis of rotation;
— angular accelerations of wheels projected onto their axis of rotation;
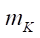 — weight of each wheel;
— weight of each wheel;
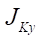 and
and 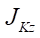 — inertia torques of the wheel relative to the corresponding axes.
— inertia torques of the wheel relative to the corresponding axes.
To form the control actions, a model of the robot dynamics described in the framework of nonholonomic mechanics is used [12]:
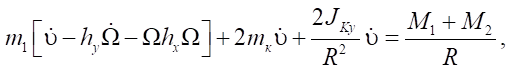
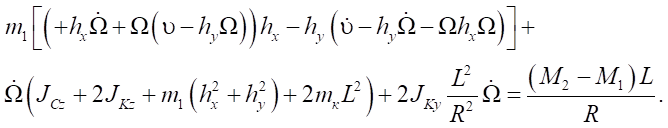 (5)
(5)
It can also be represented as:
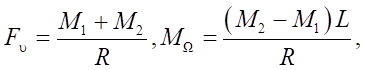 (6)
(6)
where 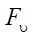 and
and 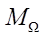 — left sides of the equation (5).
— left sides of the equation (5).
Model of engines on driving wheels. Let us describe a model of engines capable of generating control torque on driving wheels 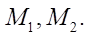
The equations of motion of wheeled DC motors can be expressed by the formulas [13]:
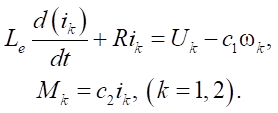 (7)
(7)
Here,
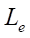 — inductance of electric motor conductors;
— inductance of electric motor conductors;
R — resistance to electric current in the motor circuit;
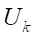 — power supply for the engine k;
— power supply for the engine k;
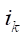 — current passing through the motor armature circuit;
— current passing through the motor armature circuit;
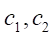 — structural constants of engines.
— structural constants of engines.
It is assumed that the drive wheel motors have the same characteristic. From (7), it can be seen that
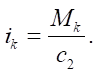 (8)
(8)
Given (8), in the first equation from system (7), we obtain a differential equation with respect to moment 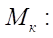
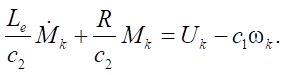 (9)
(9)
Equation (9) is divided by multiplier 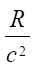 , and we get:
, and we get:
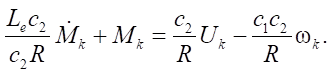 (10)
(10)
Let us introduce the notation:
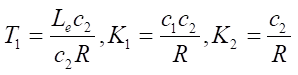 . (11)
. (11)
In this case, the control moments can be described:
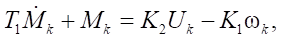 (12)
(12)
where
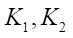 — constants;
— constants;
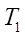 — parameter that determines the speed of transients in the electrical part of engines.
— parameter that determines the speed of transients in the electrical part of engines.
When ignoring the switching time in the electromechanical system of the engine:
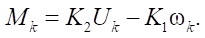 (13)
(13)
Авторы [14] получили похожие формулы.
The authors [14] obtained similar formulas.
Model under study. Let us consider models describing the dynamics of a differential drive robot.
Model 1 is described by equations (6) and (12), when the duration of transients is assumed to be vanishingly small 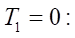
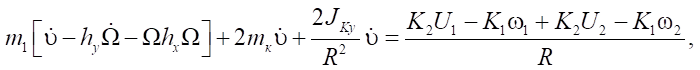
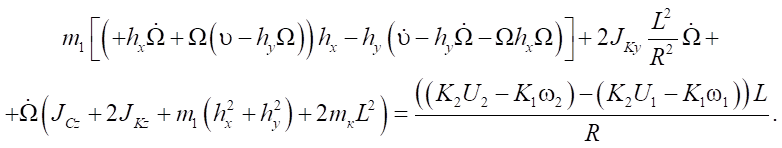 (14)
(14)
Here,  are calculated by formulas (3).
are calculated by formulas (3).
Equations (4), (13), as well as the Coulomb friction model, are used to describe Model 2:
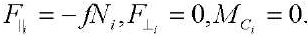 (15)
(15)
Model 3 is represented by equations (4), (12). In addition, multicomponent friction presented in [12] with the help of Pade decompositions is taken into account:
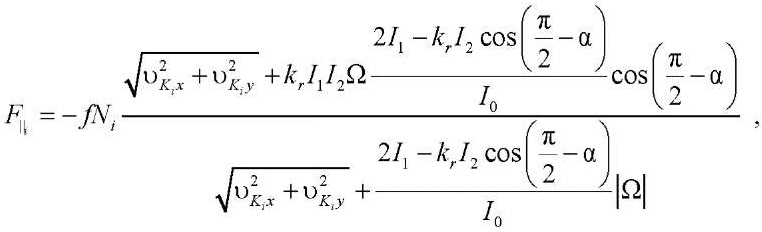 , (16)
, (16)
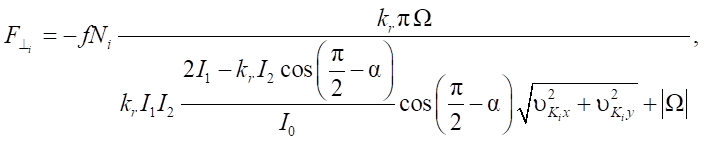 (17)
(17)
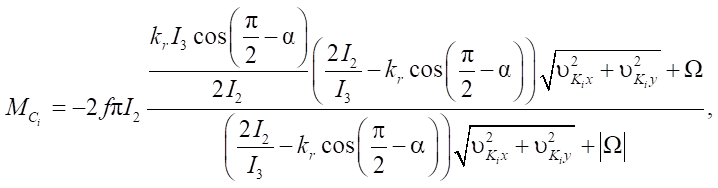 (18)
(18)
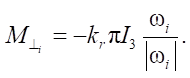 (19)
(19)
Here,
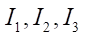 constants that are found from the formulas in [12];
constants that are found from the formulas in [12];
α — angle characterizing the direction of linear sliding speeds relative to the contact points of wheels 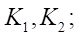
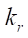 — coefficient whose sign depends on the rolling direction.
— coefficient whose sign depends on the rolling direction.
To determine the program control, the motion laws of the robot should be specified 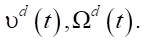 . By (5), it is possible to express values
. By (5), it is possible to express values 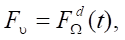
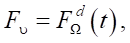
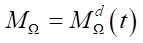 depending on time. We use known values
depending on time. We use known values 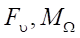 to calculate control voltages
to calculate control voltages  and
and 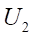 , supplied to the wheel drives:
, supplied to the wheel drives:
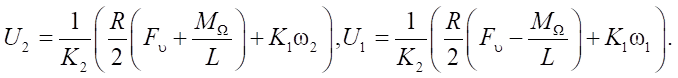 (20)
(20)
The motion of the system with the given initial conditions 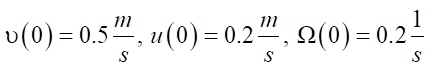 was modeled in the Wolfram Mathematica package.
was modeled in the Wolfram Mathematica package.
Consider 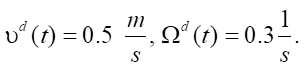 To integrate the system, the integration step was automatically selected and the built-in numerical methods of Wolfram Mathematica were used with an accuracy of the results of at least 10–6.
To integrate the system, the integration step was automatically selected and the built-in numerical methods of Wolfram Mathematica were used with an accuracy of the results of at least 10–6.
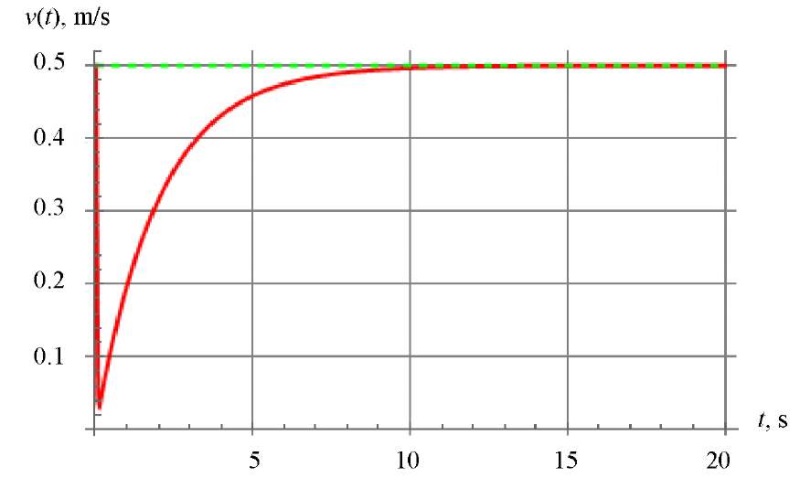
Fig. 2. Dependence of longitudinal velocity 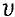 .
.
Green curve — nonholonomic model 1;
red curve — model 2 with Coulomb friction;
blue curve — model 3 with multicomponent friction.
Blue and red curves coincide
Fig. 3. Dependence of transverse velocity u.
Green curve — nonholonomic model 1;
red curve — model 2 with Coulomb friction;
blue curve — model 3 with multicomponent friction.
Green, blue and red curves coincide
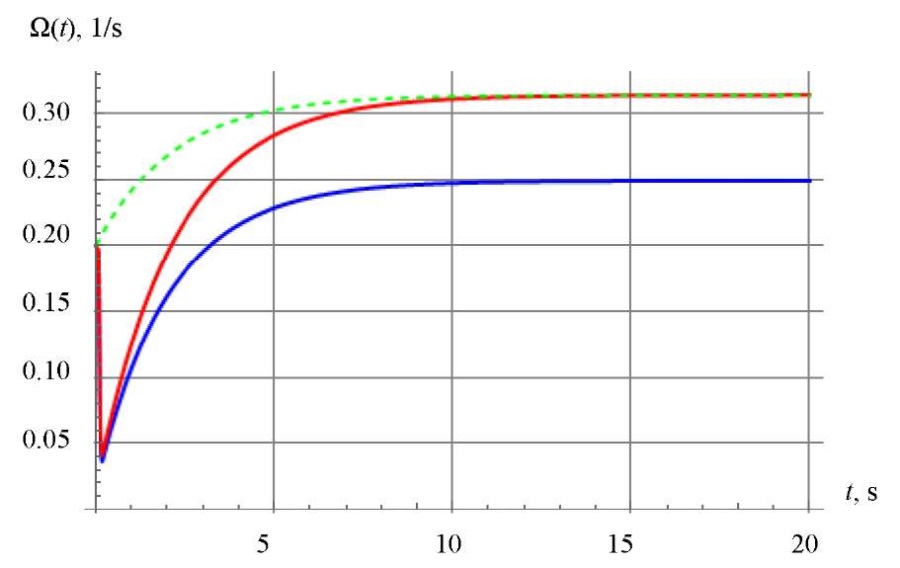
Fig. 4. Dependence of angular velocity of the robot.
Green curve — nonholonomic model 1;
red curve — model 2 with Coulomb friction,
blue curve — model 3 with multicomponent friction
Figures 2 and 4 show that the control guarantees faithful realization of the program laws of motion after the completion of transients in models 1 (nonholonomic) and 2 (with Coulomb friction). In Model 3 (multicomponent sliding, rolling and twisting friction), after the completion of transients due to software control, a constant error occurs in the angular velocity of platform rotation. In all the models considered, the sliding speed of the wheels in the transverse direction quickly decreases to zero. The cases of matching dependences obtained for different models are shown in Figures 2 and 3.
To check the fulfillment of the conditions of continuous motion of the supporting wheel, we write down the theorem on the variation of the kinetic moment of the system in projections on Y axis:
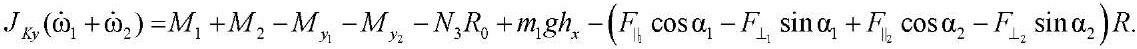
According to (4):
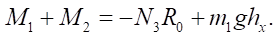
From the last equation, we obtain the condition of continuous motion of the supporting wheel:
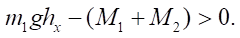
Considering (5):
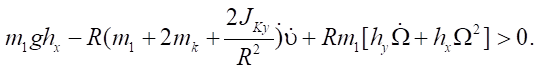
The robot's accelerations did not exceed 1 m/s2; therefore, this inequality is fulfilled at every moment of time.
Discussion and Conclusion. The simulation results allowed for drawing a number of conclusions. Software control based on nonholonomic model 1 is acceptable for robots whose design does not take into account the contact friction of the wheels that occurs under a combination of sliding, spinning and rolling. However, when forming control actions, to achieve more accurate adherence to the program motion laws, it is required to take into account the model of multicomponent friction. The resulting solution can be used to build a control system with a model predictive control. Such a development will be the subject of further research.
References
1. Gerasimov KV, Zobova AA, Kosenko II. Omni-Vehicle Dynamical Models Mutual Matching for Different Roller-Floor Contact Models. In: Proc. European Congress on Computational Methods in Applied Sciences and Engineering “Multibody Dynamics”. Cham: Springer; 2019. P. 511–517. http://doi.org/10.1007/978-3-030-23132-3_61
2. Zobova AA, Habra T, Van der Noot N, Dallali H, Tsagarakis NG, Fisette P, et al. Multi-Physics Modelling of a Compliant Humanoid Robot. Multibody System Dynamics. 2017;39:95–114. https://doi.org/10.1007/s11044-016-9545-4
3. Gerasimov KV, Zobova AA. On the Motion of a Symmetrical Vehicle with Omniwheels with Massive Rollers. Mechanics of Solids. 2018;53:32–42. https://doi.org/10.3103/S0025654418050060
4. Corke P. Robot Arm Kinematics. In book: Robotics, Vision and Control, 2nd ed. Cham: Springer; 2017. P. 193–228. https://doi.org/10.1007/978-3-319-54413-7_7
5. Junjie Shen, Dennis Hong. OmBURo: A Novel Unicycle Robot with Active Omnidirectional Wheel. In: Proc. IEEE Int. Conf. on Robotics and Automation (ICRA). New York City: IEEE; 2020. P. 11–19. https://doi.org/10.1109/ICRA40945.2020.9196927
6. Munitsyn LV. Vibrations of a Rigid Body with Cylindrical Surface on a Vibrating Foundation. Mechanics of Solids. 2017;52:675–685. https://doi.org/10.3103/S0025654417060073
7. Goryacheva IG, Zobova AA. Dynamics of Deformable Contacting Bodies with Sliding, Rolling, and Spinning. International Journal of Mechanical Sciences. 2022;216:106981. https://doi.org/10.1016/j.ijmecsci.2021.106981
8. Zobova AA, Goryacheva IG. Effect of Contacting Bodies’ Mechanical Properties on the Dynamics of a Rolling Cylinder. Acta Mechanica. 2020;232(5):1971–1982. http://doi.org/10.1007/s00707-020-02800-w
9. Kireenkov AA, Zhavoronok SI, Nushtaev DV. On Tire Models Accounting for Both Deformed State and Coupled Dry Friction in a Contact Spot. Computer Research and Modeling. 2021;13(1):163–173. https://doi.org/10.20537/2076-7633-2021-13-1-163-173
10. Kireenkov AA, Zhavoronok SI. Coupled Dry Friction Models in Problems of Aviation Pneumatics' Dynamics. International Journal of Mechanical Sciences. 2017;127:198–203. http://doi.org/10.1016/j.ijmecsci.2017.02.004
11. Kireenkov AA, Fedotenkov GV, Shiriaev A, Zhavoronok SI. Application of the Theory of the Multicomponent Dry Friction in Some of Control Robot Systems. International Journal for Computational Civil and Structural Engineering. 2022;18(1):14–23. https://doi.org/10.22337/2587-9618-2022-18-1-14-23
12. Salimov MS, Saypulaev GR, Merkuriev IV. Four-Dimensional Integral Model of Dry Friction on the Example of Wheel Movement. Journal of Physics: Conference Series. 2021;2096:012043. https://doi.org/10.1088/1742-6596/2096/1/012043
13. Alaci S, Ciornei FC, Pentiuc RD, Ciornei MC, Românu IC. Indetermination versus Incompatibility in Dynamic Systems with Dry Friction. Journal of Physics: Conference Series. 2020;1426:012011. https://doi.org/10.1088/1742-6596/1426/1/012011
14. Long Chen, Jun Liu, Hai Wang, Youhao Hu, Xuefeng Zheng, Mao Ye, et al. Robust Control of Reaction Wheel Bicycle Robot via Adaptive Integral Terminal Sliding Mode. Nonlinear Dynamics. 2021;104:2291–2302. https://doi.org/10.1007/s11071-021-06380-9
About the Authors
M. S. SalimovRussian Federation
Maksim S. Salimov, Teaching assistant of Department of Robotics, Mechatronics, Dynamics and Strength of Machines
14, Krasnokazarmennaya St., Moscow, 111250
I. V. Merkuryev
Russian Federation
Igor V. Merkuryev, Dr.Sci. (Eng.), Associate Professor, Head of the Department of Robotics, Mechatronics, Dynamics and Strength of Machines, ScopusID
14, Krasnokazarmennaya St., Moscow, 111250
Review
For citations:
Salimov M.S., Merkuryev I.V. Software Control of the Movement of a Differential Drive Robot for Different Friction Models. Advanced Engineering Research (Rostov-on-Don). 2023;23(4):346-355. https://doi.org/10.23947/2687-1653-2023-23-4-346-355. EDN: INDAIS
JATS XML














































