Перейти к:
Аппроксимация профиля лопаток газотурбинных двигателей
https://doi.org/10.23947/2687-1653-2024-24-1-78-87
EDN: QOELMG
Аннотация
Введение. Повышение долговечности лопаток газотурбинных двигателей (ГТД) достигается за счет применения специальных защитных покрытий их поверхности. Для разработки таких покрытий основной исходной информацией является геометрический профиль сечения лопатки. Для передачи заданного профиля сечения лопатки в соответствующую CAD/CAM-систему или пакет инженерного анализа применяются методы параметрического моделирования, позволяющие автоматизировать данную операцию. Однако известные подходы к созданию параметрической модели профиля лопатки не лишены ряда недостатков, и общепринятой методики ее создания в настоящее время не существует. Целью данной работы является создание методики аппроксимации профиля лопаток ГТД, удобной для использования при последующем анализе условий работы специальных покрытий поверхности лопаток.
Материалы и методы. При построении параметрических моделей профиля лопаток газотурбинных двигателей авторами использован метод, основанный на применении ортогональных полиномов Лежандра. Это позволило обеспечить высокую точность аппроксимации и построение непрерывного отображения для параметров аппроксимации профиля лопатки. Для автоматизированной обработки исходных профилей создано приложение на языке Python, позволяющее вычислять коэффициенты аппроксимирующих полиномов для линий контура лопатки, визуализировать результаты расчета и создавать по точкам аппроксимирующих функций dxf-файл для передачи его в CAD-систему. Далее геометрические модели лопаток использовали для решения задачи обтекания лопатки стационарным аэродинамическим потоком. Результаты решения этой задачи использованы при исследовании влияния профиля лопатки на ее остывание в аэродинамическом потоке.
Результаты исследования. В качестве примера рассмотрены три варианта профилей лопаток, относящихся к разным типам ГТД. Показано, что для всех трех изученных профилей предложенная методика позволяет получать параметрические модели, обеспечивающие высокую точность построения аппроксимирующих линий, что подтверждается близкими к единице значениями коэффициентов детерминации. Для иллюстрации возможности использования полученных моделей приведены примеры решения задачи газовой динамики при потенциальном обтекании лопатки в стационарном аэродинамическом потоке. Методом конечных элементов рассчитаны распределения давлений и температур на поверхности лопатки.
Обсуждение и заключение. Результаты вычислений показали, что предлагаемая методика аппроксимации профиля лопатки ГТД, основанная на использовании ортогональных многочленов, является удобным инструментом, позволяющим автоматизировать создание геометрической модели лопатки и проводить сравнение различных типов и профилей лопаток, решая соответствующие задачи газовой динамики. При этом для заданного профиля лопаток и условий работы ГТД можно получить распределение температур и усилий, действующих на поверхности лопатки, что необходимо для прогнозирования долговечности специальных покрытий
Ключевые слова
Для цитирования:
Соловьев М.Е., Шулева Ю.Н., Балдаев С.Л., Балдаев Л.Х. Аппроксимация профиля лопаток газотурбинных двигателей. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):78-87. https://doi.org/10.23947/2687-1653-2024-24-1-78-87. EDN: QOELMG
For citation:
Soloviev M.E., Shuleva Yu.N., Baldaev S.L., Baldaev L.Kh. Approximation of the Profile of Gas Turbine Engine Blades. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):78-87. https://doi.org/10.23947/2687-1653-2024-24-1-78-87. EDN: QOELMG
Введение. Лопатки турбины являются наиболее высоконагруженными деталями газотурбинного двигателя, долговечность которых главным образом определяет межремонтный ресурс двигателя [1]. Одним из путей повышения долговечности лопаток турбин является нанесение специальных защитных покрытий на их поверхности [2]. Покрытие представляет собой сложную композитную конструкцию, для выбора материалов которой и определения оптимальных геометрических характеристик необходимо знать условия эксплуатации детали: распределение температур, давлений и сдвиговых напряжений на поверхности лопатки.
К форме лопаток, а также к выбору материалов, технологии их изготовления и специальных покрытий предъявляются самые высокие требования [3]. При проектировании специальных покрытий основной исходной информацией является геометрический профиль поверхности детали, поскольку на его основе задаются параметры технологического процесса нанесения покрытия.
Среди характерных элементов профиля можно выделить: хорду — расстояние между наиболее удаленными точками при горизонтальном расположении лопатки, подобно крылу самолета, спинку (suction side) — верхнюю часть профиля, корытце (pressure side) — нижнюю часть профиля, входные и выходные кромки [4]. Выбор формы профиля сечения лопаток производится как на основе экспериментальных исследований опытных установок и реальных двигателей [5], так и по результатам численных экспериментов на моделях [6]. В процессе численного моделирования возникает задача создания геометрической модели лопатки на основании заданного профиля сечения и передачи ее в соответствующую CAD/CAM-систему [7] или пакет инженерного анализа [8], в котором задаются параметры физических свойств материалов деталей, определяются граничные условия задачи и осуществляются вычисления.
Традиционно при создании чертежа лопатки ее профиль описывается набором дуг окружностей, который затем по точкам передается в модуль создания геометрической модели и генерации сетки конечных элементов. Недостаток данного подхода состоит в том, что при создании каждой новой модели приходится вручную создавать в графическом редакторе ее профиль. В этой связи были предложены методы параметрического моделирования профиля сечения лопатки, позволяющие автоматизировать данную операцию. Одной из наиболее известных таких моделей является девятипараметрическая модель RATD (Rapid Axial Turbine Designe), предложенная в работе [9]. Вместе с тем практика использования RATD выявила и определенные недостатки, свойственные данной модели, в частности неудобство использования при оптимизации геометрии профиля, а также недостаточную точность. На этом основании авторами [10] была предложена модифицированная версия данной модели, включающая в себя большее число параметров. В отечественной практике также активно используются методы параметрического моделирования профилей сечения лопаток. Так, в работах [11][12] были предложены алгоритмы автоматизированного построения профиля лопаток с использованием аппроксимации кривыми из набора парабол и кривыми Bezier второго порядка. В работе [13] на основе данных алгоритмов предложена методика проектирования решетки профилей ГТД. Использование параметрических моделей профилей лопаток при решении задач оптимизации рассматривалось авторами в [14][15].
Вместе с тем следует отметить, что существующие методики параметризации профиля лопаток не лишены ряда недостатков. Основной недостаток традиционных схем параметризации профиля лопаток, основанных на использовании кривых второго порядка, состоит в том, что для обеспечения точности описания приходится использовать различные функции для разных частей детали. При этом данные функции не образуют ортогональную систему, а значения параметров, определяемых аппроксимацией существующего профиля методом наименьших квадратов, оказываются скоррелированными. Это приводит к тому, что не удается построить непрерывного отображения для множества параметров при аппроксимации системой сечений трехмерной поверхности лопатки двойной кривизны.
Также необходимо отметить, что универсальной методики параметрического моделирования профилей лопаток ГТД в настоящий момент не существует, а выбор конкретной методики зависит как от целей моделирования, так и от особенностей конкретного типа проектируемого двигателя. Вместе с тем формы входной информации могут существенно различаться. Это может быть и геометрическая модель в виде файла в формате одной из CAD-систем, и просто набор точек из базы данных профилей типа [16].
Таким образом, дополнительным требованием к методике параметрического моделирования профиля лопаток, обусловленным назначением модели, является универсальность по отношению к формату исходных данных.
Целью настоящей работы явилось создание методики аппроксимации профиля лопаток ГТД, свободной от вышеперечисленных недостатков и удобной для использования при последующем анализе условий работы специальных покрытий поверхности лопаток, что продемонстрировано на примере решения задачи газовой динамики для трех различных моделей лопаток, профиль которых параметризован с применением предлагаемой методики.
Материалы и методы. Авторами использован вариант параметрических моделей профиля лопаток, основанный на использовании ортогональных полиномов Лежандра [17]. Для автоматизированной обработки исходных профилей было создано приложение на языке Python, позволяющее вычислять коэффициенты аппроксимирующих полиномов для линий контура лопатки, визуализировать результаты расчета в форме графиков исходных точек и аппроксимационных кривых для спинки и корытца лопатки, сохранять исходные точки профиля, массив коэффициентов аппроксимирующих полиномов и коэффициент детерминации модели в базе данных и создавать по точкам аппроксимирующих функций dxf-файл для передачи его в CAD-систему и пакет инженерного анализа.
Построенные двумерные геометрические модели лопаток использовали для решения задачи обтекания лопатки стационарным аэродинамическим потоком в приближении потенциального обтекания. Вычисленные в результате решения этой задачи распределения скоростей в потоке использовали при исследовании влияния профиля лопатки на ее остывание в аэродинамическом потоке.
Методика расчета. Системы ортогональных многочленов, используемые в качестве основы предлагаемого метода, обеспечивают линейную независимость коэффициентов аппроксимации и лишены недостатка, приводящего
к затруднениям при построении моделей, непрерывных по параметрам. Степень полиномов выбрана достаточно высокой — девятого порядка, так что набор из двух полиномов для двух частей профиля (спинки и корытца) составляет двадцать параметров, что является достаточным для аппроксимации весьма сложных профилей. Ниже описаны вид аппроксимирующей функции и методика вычисления оценок ее коэффициентов.
Обозначим аппроксимирующую линию профиля лопатки посредством функции y(x). Выражение данной линии в случае ряда полиномов Лежандра девятой степени представим в виде:
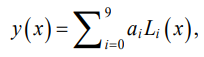 (1)
(1)
где ai — коэффициенты, являющиеся параметрами модели; Li(x) — полиномы Лежандра, вычисляемые по формулам:
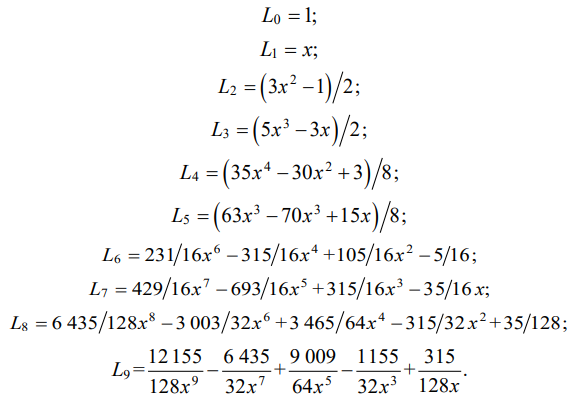 (2)
(2)
Пусть координаты исходного профиля лопатки заданы набором точек 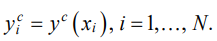 Подставляя значения xi в функции (2), получим матрицу X размером N × 10. Коэффициенты аппроксимирующего полинома для заданных профилей лопаток находили методом наименьших квадратов из условия минимума суммы квадратов отклонений заданных значений
Подставляя значения xi в функции (2), получим матрицу X размером N × 10. Коэффициенты аппроксимирующего полинома для заданных профилей лопаток находили методом наименьших квадратов из условия минимума суммы квадратов отклонений заданных значений 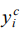 и рассчитанных по уравнению регрессии (1):
и рассчитанных по уравнению регрессии (1):
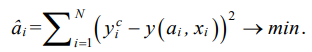 (3)
(3)
Оценки коэффициентов 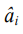 вычисляли с помощью известной формулы регрессионного анализа:
вычисляли с помощью известной формулы регрессионного анализа:
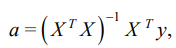 (4)
(4)
где a — обозначение для вектора оценок коэффициентов; y — для вектора точек заданного профиля 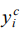
Точность аппроксимации оценивалась по коэффициенту детерминированности модели (коэффициент детерминации R2), который при хорошей аппроксимации должен быть близким к единице:
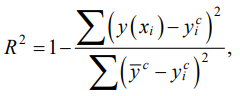 (5)
(5)
где 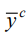 — среднее значение
— среднее значение 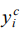
В конструкторской практике принято входную и выходную кромки контура лопаток описывать радиусами окружностей. В связи с этим в данной работе рассматривались координаты точек аппроксимируемых профилей между дугами окружностей входной и выходной кромок. Для целей аппроксимации расположение контура рассматриваемой лопатки было принято горизонтальным, так, чтобы линия хорды лопатки совпадала с осью абсцисс декартовой системы координат. Для сохранения условия ортогональности моделей обязательным является нормировка размеров. В связи с этим все размеры нормировались на длину хорды лопатки, так что абсциссы точек профиля лежали в интервале 0,1. Это обеспечивало ортогональность функций (2) с коэффициентами, вычисленными по формулам (4).
Результаты исследования. В таблице 1 приведены коэффициенты аппроксимирующих полиномов для профилей лопаток, относящихся к разным типам ГТД: профиль лопатки компрессора С8626 [13], профиль NASA лопатки высокоэффективного ГТД высокого давления [18] и профиль лопатки-имитатора, использованной в работе [19] для исследования термической усталости теплозащитного покрытия, состоящего из двух металлических и керамического слоев.
Таблица 1
Коэффициенты аппроксимирующих полиномов для профилей лопаток из разных источников
Коэффициенты | [13] | [18] | [19] | |||
спинка | корытце | спинка | корытце | спинка | корытце | |
142,4250 | –123,0993 | –1275,6471 | 717,8336 | –1043,6707 | 527,0915 | |
–374,3446 | 324,9875 | 3328,6126 | –1868,9670 | 2719,5055 | –1369,9895 | |
477,9332 | –417,7186 | –4181,1239 | 2338,1048 | –3406,1466 | 1707,9198 | |
–444,4554 | 392,7204 | 3794,0526 | –2108,4202 | 3077,0694 | –1531,8025 | |
324,6819 | –292,0489 | –2684,7257 | 1479,0172 | –2164,2992 | 1066,1471 | |
–189,2284 | 174,3673 | 1502,4170 | –818,4219 | 1201,7203 | –583,7501 | |
86,8260 | –82,4103 | –654,4877 | 351,5869 | –518,2516 | 247,3087 | |
–30,0775 | 29,5457 | 211,8930 | –111,9355 | 165,6344 | –77,2958 | |
7,1533 | –7,3024 | –46,0284 | 23,8450 | –35,3931 | 16,0493 | |
–0,9024 | 0,9652 | 5,1021 | –2,5861 | 3,8411 | –1,6752 | |
0,9999 | 0,9993 | 0,9896 | 0,9990 | 0,9982 | 0,9994 | |
На рис. 1 приведены исходные точки данных профилей и соответствующие аппроксимирующие линии
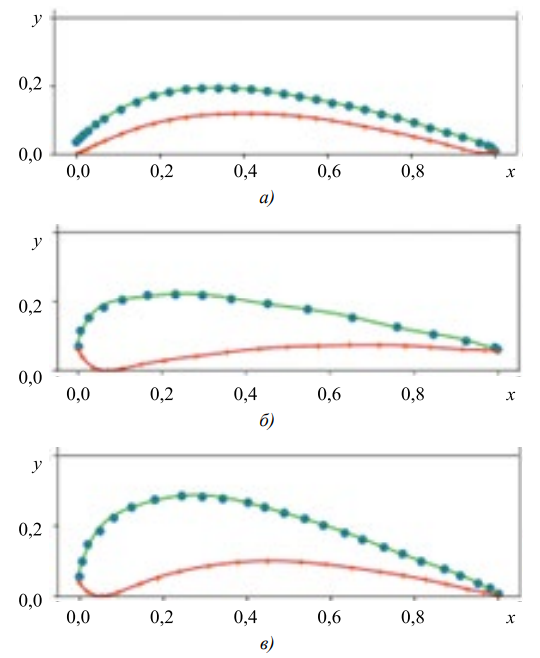
Рис. 1. Исходные точки и аппроксимирующие линии профилей лопаток, представленных в таблице 1, источники профилей лопаток: а — [13]; б — [18]; в — [19]
Как было указано выше, целью параметризации в настоящей работе является аппроксимация профиля непрерывной функцией с последующим моделированием распределения внешних параметров по поверхности лопатки. Для иллюстрации возможности решения данной задачи рассмотрим простую двумерную модель лопатки в стационарном аэродинамическом потоке, в приближении потенциального обтекания. В этом случае распределение скоростей потока v(x, y) описывается уравнением:
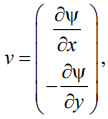 (6)
(6)
где функция ψ находится из решения уравнения Лапласа:
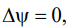 (7)
(7)
которое в данном случае отвечает условию несжимаемости (∇ ∙ v = 0) и безвихревому потоку (∇ × v = 0).
Граничным условием для функции ψ будет являться равенство нулю скорости в нормальном направлении поверхности лопатки, что означает постоянство ψ на этой поверхности.
Обозначим линию профиля поверхности лопатки посредством S и будем искать решение уравнения (7) в области Ω, ограниченной внешней частью по отношению к S и внутренней частью по отношению к окружности C достаточно большого диаметра, по сравнению с длиной хорды лопатки, так что на поверхности C поток является однородным. То есть на границе области 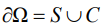 заданы условия:
заданы условия:
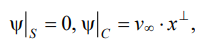 (8)
(8)
где 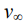 — вектор скорости однородного потока.
— вектор скорости однородного потока.
После вычисления скоростей можно вычислить распределение давлений по уравнению Бернулли:
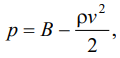 (9)
(9)
где ρ — плотность газа; B — постоянная Бернулли, которую можно положить равной 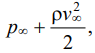 где
где 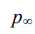 — давление на бесконечном удалении от лопатки.
— давление на бесконечном удалении от лопатки.
Вариационная постановка задачи (7) выглядит следующим образом:
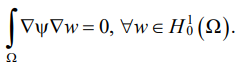 (10)
(10)
Решение данной задачи осуществлялось методом конечных элементов. Для сравнения расчет был проведен для трех вариантов профилей лопаток, приведенных в таблице 1, с одной и той же длиной хорды l.
Полученные результаты использовались далее при решении задачи остывания лопатки в аэродинамическом потоке. Такая задача имеет смысл при термоциклических испытаниях покрытий на лопатках-имитаторах. В этом случае постановка задачи выглядела следующим образом:
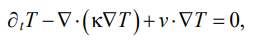 (11)
(11)
где T — температура; t — время; κ — коэффициент температуропроводности.
Начальное распределение температуры:
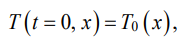 (12)
(12)
было принято следующим: внутри лопатки постоянная температура 400 °С, температура окружающей среды 0 °С. Граничные условия отвечали отсутствию теплового потока на внешнем контуре C:
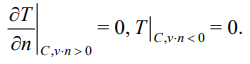 (13)
(13)
Распределение скоростей потока в задаче (11) вычислялось при решении задачи (10), при этом скорость на контуре C принята равной v = 10[l/c] (размерность длины в единицах длины хорды). Коэффициенты теплопроводности лопатки и газа приняты равными 0,1 и 0,01 [l2/c] соответственно.
Программный код для решения задач (10), (11) был написан на входном языке универсального конечно-элементного пакета FreeFem++ [20].
На рис. 2 приведены рассчитанные в результате решения задач (11), (12) распределения давления и температуры при остывании лопатки в течение 25 с. в аэродинамическом потоке для трех изученных профилей лопаток, представленных на рис. 1. В таблице 2 приведены вычисленные по ним значения минимальных относительных давлений вблизи поверхностей лопаток и максимальные температуры лопаток.

Рис. 2. Рассчитанные распределения давления (p, слева) и температуры (T, справа) при моделировании обтекания и остывания в потоке лопаток исследованных профилей (обозначения профилей — как на рис. 1). Угол направления вектора потока с направлением хорды лопатки составлял 10°
Таблица 2
Минимальное относительное давление вблизи поверхности лопатки и максимальная температура лопатки после 25 с остывания в аэродинамическом потоке
Параметры | Профиль лопатки | ||
[13] | [18] | [19] | |
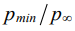 | 0,599 | 0,699 | 0,720 |
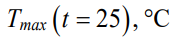 | 156,9 | 245,2 | 263,4 |
Обсуждение и заключение. Судя по данным, представленных в таблице 1, коэффициенты детерминации для всех изученных профилей лопаток близки к единице несмотря на то, что формы профилей существенно различались. Это подтверждает хорошее качество аппроксимации и иллюстрируется также данными на рис. 1. Таким образом, предложенный метод позволяет с высокой точностью построить аппроксимирующие линии профилей лопаток для различных типов ГТД.
В работе также проиллюстрирована возможность использования аппроксимирующих функций при расчете распределения давлений и температур на поверхности лопатки на основании решения задачи газовой динамики. Далее данное распределение может быть использовано при оптимизации структуры специальных покрытий лопатки, например теплозащитных покрытий. Данные, представленные на рис. 2 и в таблице 2, подтверждают, что данная задача также может быть успешно решена. Характеры распределений давлений и температур для разных профилей лопаток имеют общие черты, но детальная картина различается. Видно в частности, что лопатка профиля [19], имеющая большую, по сравнению с остальными, площадь сечения, характеризуется большим значением относительного давления в зоне выходной кромки и меньшей скоростью остывания. Это иллюстрируется также данными, приведенными в таблице 2. Поскольку с точки зрения прочности адгезионной связи покрытия с подложкой наиболее опасными являются усилия, направленные нормально от поверхности лопатки, то актуальным является относительное минимальное давление вблизи поверхности, значения которого представлены в таблице 2. На основании полученного расчета можно обоснованно подойти к проектированию специального покрытия поверхности лопатки конкретного профиля: регулировать материалы и толщину покрытия в зависимости от степени нагруженности отдельных зон поверхности.
Заметим, что данные результаты расчетов представлены лишь в качестве иллюстрации возможностей предложенной методики аппроксимации профилей. Поэтому использованная в работе модель газовой динамики была достаточно упрощенной. В конкретной задаче необходимо использовать более строгую модель с параметрами, отвечающими заданному типу и режиму работы ГТД.
Таким образом, предлагаемая методика аппроксимации профиля лопатки ГТД, основанная на использовании ортогональных многочленов, является удобным инструментом, позволяющим автоматизировать создание геометрической модели лопатки и проводить сравнение различных типов и профилей лопаток, решая соответствующие задачи газовой динамики. При этом для заданного профиля лопаток и условий работы ГТД можно получить распределение температур и усилий, действующих на поверхности лопатки, что необходимо для прогнозирования долговечности специальных покрытий [21]. На основе данного расчета можно оптимизировать технологию нанесения покрытия, варьируя его толщину и/или состав, увеличивая коэффициент запаса долговечности в наиболее опасных областях.
Список литературы
1. Крымов В.В., Елисеев Ю.С., Зудин К.И. Производство лопаток газотурбинных двигателей. Москва: Машиностроение; 2002. 376 с.
2. Панков В.П., Бабаян А.Л., Куликов М.В., Коссой В.А., Варламов Б.С. Теплозащитные покрытия лопаток турбин авиационных газотурбинных двигателей. Ползуновский вестник. 2021;1:161–172.
3. Nirmith Kumar Mishra, Shyam Raja Puppala, Laxmi Teja Kolanu, Jyoshnavi Amudapuram, Ratan Makthal. Design and Analysis of a Gas Turbine Blade. AIP Conference. Proceedings. 2023;2492(1):020040. https://doi.org/10.1063/5.0113346
4. Cohen H, Rogers GFC, Straznicky P, Saravanamuttoo HIH, Nix A. Gas Turbine Theory, 7th Ed. London: Pearson; 2017. 606 p.
5. Jabbar A, Rai AK, Reddy PR, Dakhil MH. Design and Analysis of Gas Turbine Rotor Blade Using Finite Element Method. International Journal of Mechanical and Production Engineering Research and Development. 2014;4(1): 91–112.
6. Win Lai Htwe, Htay Htay Win, Nyein Aye San. Design and Thermal Analysis of Gas Turbine Blade. International Journal of Mechanical and Production Engineering. 2015;3(7):62–66. URL: https://www.iraj.in/journal/journal_file/journal_pdf/2-165-143653913462-66.pdf (accessed: 14.12.2023).
7. Leloudas SN, Eskantar AI, Lygidakis GN, Nikolos LK. Low Reynolds Airfoil Family for Small Horizontal Axis Wind Turbines Based on RG15 Airfoil. SN Applied Sciences. 2020;2:371. https://doi.org/10.1007/s42452-020-2161-1
8. Eftekhari S, Al-Obaidi ASM. Investigation of a NACA0012 Finite Wing Aerodynamics at Low Reynold’s Numbers and 0° to 90° Angle of Attack. Journal of Aerospace Technology and Management. 2019;11(1):e1519. URL: https://www.scielo.br/j/jatm/a/JdnMCtH6R3PhTBZ69YNqNfd/?format=pdf&lang=en (accessed: 14.12.2023).
9. Pritchard LJ. An Eleven Parameter Axial Turbine Airfoil Geometry Model. In: Proc. ASME International Gas Turbine Conference and Exhibition. Vol. 1: Aircraft Engine; Marine; Turbomachinery; Microturbines and Small Turbomachinery. New York: ASME; 1985. https://doi.org/10.1115/85-GT-219
10. Mengistu T, Ghaly W, Mansour T. Aerodynamic Shape Optimization of Turbine Blades Using a Design-Parameter-Based Shape Representation. In: Proc. ASME Turbo Expo 2007: Power for Land, Sea, and Air. Vol. 6: Turbo Expo 2007, Parts A and B. New York: ASME; 2007. https://doi.org/10.1115/GT2007-28041
11. Виноградов Л.В., Алексеев А.П. Костюков А.В. Профиль лопатки турбины из кривых Bezier. Вестник РУДН. Cерия: Инженерные исследования. 2013;3:10–15.
12. Виноградов Л.В., Мамаев В.К., Ощепков П.П. Турбинный профиль A3K7-NACA: автоматизация проектирования. Вестник РУДН. Серия: Инженерные исследования. 2017;18(3):299–307.
13. Мамаев В.К., Виноградов Л.В., Ощепков П.П. Моделирование решетки профилей транспортного газотурбинного двигателя. Вестник РУДН. Серия: Инженерные исследования. 2019;20(2):140–146. https://doi.org/10.22363/2312-8143-2019-20-2-140-146
14. Шаблий Л.С., Колмакова Д.А., Кривцов А.В. Параметрическое моделирование лопаточных машин при оптимизации. Известия Самарского научного центра Российской академии наук. 2013;15(6–4):1013–1018.
15. Блинов В.Л., Бродов Ю.М., Седунин В.А. Комаров О.В. Параметрическое профилирование плоских компрессорных решеток при решении задач многокритериальной оптимизации. Известия высших учебных заведений. Проблемы энергетики. 2015;(3–4):86–95.
16. Schnoes M, Nicke E. Exploring a Database of Optimal Airfoils for Axial Compressor Design. ISABE. 2017;21493:1–17.
17. Beals R, Wong R. Special Functions and Orthogonal Polynomials. Cambridge: Cambridge University Press; 2016. 473p. https://doi.org/10.1017/CBO9781316227381
18. Timko LP. Energy Efficient Engine High Pressure Turbine Component Test Performance Report. Washington, DC: NASA; 1984. 173 p.
19. Тихомирова Е.А., Будиновский С.А., Живушкин А.А., Сидохин Е.Ф. Особенности развития термической усталости в деталях из жаропрочных сплавов с покрытием. Авиационные материалы и технологии. 2017;48(3):20–25.
20. Hecht F. FreeFEM Documentation. Release 4.6. Paris: Sorbonne University; 2021. 673 p.
21. Соловьев М.Е., Раухваргер А.Б., Балдаев С.Л., Балдаев Л.Х. Кинетическая модель разрушения адгезионного соединения порошкового покрытия и металлического субстрата. Наукоёмкие технологии в машиностроении. 2023;139(1):9–19. https://doi.org/10.30987/2223-4608-2023-1-9-19
Об авторах
М. Е. СоловьевРоссия
Михаил Евгеньевич Соловьев, доктор физико-математических наук, профессор кафедры информационных систем и технологий
150023, г. Ярославль, Московский пр-т, 88
Ю. Н. Шулева
Россия
Юлия Николаевна Шулева, ассистент кафедры информационных систем и технологий
150023, г. Ярославль, Московский пр-т, 88
С. Л. Балдаев
Россия
Сергей Львович Балдаев, заместитель генерального директора по технологиям
108851, г. Москва, г. Щербинка, ул. Южная, 9а
Л. Х. Балдаев
Россия
Лев Христофорович Балдаев, генеральный директор
108851, г. Москва, г. Щербинка, ул. Южная, 9а
Рецензия
Для цитирования:
Соловьев М.Е., Шулева Ю.Н., Балдаев С.Л., Балдаев Л.Х. Аппроксимация профиля лопаток газотурбинных двигателей. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):78-87. https://doi.org/10.23947/2687-1653-2024-24-1-78-87. EDN: QOELMG
For citation:
Soloviev M.E., Shuleva Yu.N., Baldaev S.L., Baldaev L.Kh. Approximation of the Profile of Gas Turbine Engine Blades. Advanced Engineering Research (Rostov-on-Don). 2024;24(1):78-87. https://doi.org/10.23947/2687-1653-2024-24-1-78-87. EDN: QOELMG












































