Содержание
Перейти к:
Повышение межслойной трещиностойкости полимерных тканевых композитов с помощью локального трехмерного армирования (фелтинга)
https://doi.org/10.23947/2687-1653-2024-24-3-215-226
EDN: KVEMQM
Аннотация
Введение. Одна из причин нежелательных расслоений полимерных композитов с тканевым армированием — низкие трансверсально-сдвиговые характеристики. Известно, что армирование полимерных тканевых композитов в направлении Z уменьшает чувствительность к расслоению и повышает вязкость межслойного разрушения. В литературе предлагаются разные способы трехмерного армирования полимерных тканевых композитов. Однако они усложняют процесс изготовления конструкции. Проблему решает предложенный в данной статье способ трехмерного армирования — фелтинг. Это локальное армирование композита в направлении Z при минимальных производственных изменениях. Степень Z-армирования определяется плотностью фелтинга, т.е. количеством ударов иглы на 1 см² тканевого пакета. Цель работы — оценить влияние фелтинга на межслойную трещиностойкость композитного материала.
Материалы и методы. Межслойную вязкость разрушения GIIc определяли на стеклоткани полотняного переплетения с фелтингом 10 см–². Материал пропитывали смолой Этал-370 и отвердителем Этал-45. Эксперименты по стандартам ASTM D7905M–14 и ГОСТ 33685–2015 проводили на испытательной машине Instron 5900R. Напряженное состояние у вершины трещины анализировали с позиции нелокальной теории прочности в программе Ansys Workbench (опция «статический прочностной анализ»). Задействовали метод конечных элементов (МКЭ).
Результаты исследования. Для образцов рассмотрели кривые «нагрузка — перемещение». Вычислили значения GIIс. Обобщили итоги ENF-испытаний для плотности фелтинга 0 см–² и 10 см–². Сравнили контрольные образцы и образцы с фелтингом. В последнем случае GIIс оказалась выше на ~33 %. Рассчитали напряженное состояние у вершины трещины при DCB- и ENF-нагружении. Визуализировали в виде графиков и цветовых диаграмм зависимости максимальных нормальных и касательных напряжений, а также перемещений. Для получения расчетных зависимостей «нагрузка — перемещение» с помощью МКЭ использовали обратный метод получения трансверсально-сдвиговых констант. Нагружение по схеме DCB показало, что фелтинг позволяет увеличить предел прочности на растяжение в направлении Z на ~18 %, с 39 до 46 МПа, а в плоскости XZ — на ~16 %, с 77 МПа до 89 МПа.
Обсуждение и заключение. Фелтинг как способ локального трехмерного армирования усиливает межслойную трещиностойность полимерных тканевых композитов. Он позволяет сократить площадь расслоений после локальных ударов при эксплуатации конструкций. Гибкая технология фелтинга дает возможность создавать зоны с произвольной плотностью ударов, повышая трещиностойкость лишь в необходимых местах конструкций. МКЭ-анализ напряженного состояния у вершины трещины в рамках нелокальной теории прочности показал, что в прочностных расчетах трещину расслоения можно рассматривать как концентратор напряжений.
Ключевые слова
армирование полимерных тканевых композитов,
трансверсально-сдвиговая прочность,
межслойная трещиностойкость,
межслоевая вязкость разрушения,
фелтинговое локальное трехмерное армирование
При поддержке: Исследование выполнено в рамках Программы создания и развития научного центра мирового уровня «Сверхзвук» на 2020–2025 годы при финансовой поддержке Минобрнауки России (соглашение от 17 мая 2022 г. № 075–15–2022–1023).
Для цитирования:
Форенталь Г.А., Сапожников С.Б. Повышение межслойной трещиностойкости полимерных тканевых композитов с помощью локального трехмерного армирования (фелтинга). Advanced Engineering Research (Rostov-on-Don). 2024;24(3):215-226. https://doi.org/10.23947/2687-1653-2024-24-3-215-226. EDN: KVEMQM
For citation:
Forental G.А., Sapozhnikov S.B. Increasing the Interlayer Fracture Toughness of Polymer Fabric Composites Using Local 3D-Reinforcement (Felting). Advanced Engineering Research (Rostov-on-Don). 2024;24(3):215-226. https://doi.org/10.23947/2687-1653-2024-24-3-215-226. EDN: KVEMQM
Введение. Волокнистые полимерные композиты широко применяются в авиационной и космической технике благодаря значительной жесткости и прочности в направлении укладки волокон (плоскость XY) [1]. Однако трансверсально-сдвиговая прочность этих материалов достаточно низкая [2], так как определяется особенностями полимерной матрицы [3]. Армирование полимерных тканевых композитов в направлении Z позволяет уменьшить чувствительность к расслоению, т.е. повысить вязкость межслойного разрушения [4].
Известны различные методы трехмерного армирования полимерных тканевых композитов [5]. Однако они создают дополнительные сложности при изготовлении конструкций из полимерных тканевых композитов [6]. Предложенный в данной работе способ трехмерного армирования — фелтинг [7] позволяет получить локально армированный в направлении Z композит при минимальных изменениях в процессе производства. Степень
Z-армирования при этом определяется плотностью фелтинга, т.е. количеством ударов иглой на 1 см2 площади тканевого пакета [8].
Использование различных методик определения трещиностойкости полимерных композитных материалов [9] позволяет проводить исследования на различных образцах [10] и при различных способах нагружения [11]. Один из самых распространенных подходов — метод трехточечного изгиба. В этом случае используется образец с расслоением в виде балки. Речь идет о ENF-испытаниях (от англ. end notched flexure — изгиб образца с краевым расслоением) [12], что предполагает нагружение поперечным сдвигом. Это дает возможность определить межслоевую вязкость разрушения GIIc — разрушение по моде II. В вершине трещины возникают высокие касательные напряжения [13].
Еще один распространенный способ определения трансверсальных характеристик — метод двухконсольной балки (DCB-испытания (от англ. double cantilever beam — двухконсольная балка)). При DCB-испытаниях значение межслоевой вязкости разрушения GIc определяется при нагружении отрывом — разрушение по моде I [14]. Трещина расслоения распространяется за счет действия нормальных напряжений [15].
Цель представленной работы — оценить влияние фелтинга на межслойную трещиностойкость композитного материала. Для этого провели ENF-испытания (изгиб образца с краевым расслоением) композитного материала, обладающего повышенной трещиностойкостью за счет применения фелтинга. Ранее авторы изучали влияние фелтинга на межслойную трещиностойкость композитного материала при DCB-испытаниях [16]. Создали расчетную модель, основанную на нелокальной теории прочности. Она позволяет с помощью метода конечных элементов (МКЭ) для трещин различной длины рассчитать напряжения, возникающие в образцах ENF и DCB.
Материалы и методы
Экспериментальное определение межслойной трещиностойкости методом ENF. Образцы изготавливали из стеклоткани полотняного переплетения с толщиной слоя 0,2 мм. Пакет сухой стеклоткани из двух слоев пробивали на фелтинговой машине с плотностью фелтинга 10 см–2 (на 1 см2 сухой стеклоткани приходится 10 ударов иглой фелтинговой машины). Пакет стеклоткани пробивали таким образом, чтобы после пропитки и отверждения начальная трещина не попадала на область фелтинга. Для создания начальной трещины между двумя слоями стеклоткани помещали алюминиевую фольгу толщиной 11 мкм, покрытую разделительной смазкой Вс-М. Стеклоткань пропитывали смолой Etal-370 и отвердителем Etal-45. Для изготовления контрольных образцов два слоя сухой стеклоткани пропитали смолой Etal-370 и отвердителем Etal-45 без пробивки на фелтинговой машине. После пропитки к двум слоям стеклоткани приклеивали пластины из стеклопластика СТЭФ (рис. 1 а). Образцы длиной 150 мм и шириной 16 мм получали путем разрезания отвержденных пластин с помощью высокоскоростной дисковой пилы.
Рис. 1. Конфигурация и параметры испытаний ENF по моде II:
а — схема нагружения; б — фото испытаний
Задействовали испытательную машину Instron 5900R со скоростью нагружения 10 мм/мин. Расстояние между опорами 2L = 100 мм. Начальная длина трещины у всех образцов a0 = 25 мм. Для выполнения калибровки податливости в широком диапазоне длин трещины разгрузили и снова нагрузили по одному образцу каждого типа. Образовавшаяся трещина служила начальной трещиной в следующем цикле нагружения.
Для обработки результатов испытаний использовали калибровку, рекомендованную стандартами ASTM D7905M–141 и ГОСТ 33685–20152. Такой подход позволяет определить параметры А и m для каждого образца c фелтингом и каждого контрольного образца без фелтинга из линейной зависимости двух величин — податливости образца Си куба длины трещины а³:
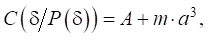(1)
где Р — нагрузка, прикладываемая к образцу; d — перемещение.
После калибровки и определения параметров А и m можно найти длину трещины из выражения (1):
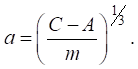(2)
Момент начала расслоения определяется условием C(d) = C(Pmax). Значение межслойной вязкости разрушения при начале отслоения (развитие трещины):
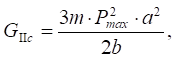(3)
где Pmax — максимальная нагрузка; a — длина трещины, рассчитанная по формуле (2) при нагрузке Pmax;
b — ширина образца.
Расчет напряженного состояния у вершины трещины при нагружении по схемам DCB и ENF. Оценка напряженного состояния у трещиноподобного концентратора проведена с позиции подходов, которые используют нелокальные напряжения [17], т.е. осредненные на некоторой базе [18]. В расчетную модель также закладывали допущение о линейно-упругом поведении материала вплоть до разрушения [16].
Основная гипотеза: за развитие трещиноподобного концентратора ответственен критерий прочности композита, включающий все компоненты осредненных на базе l напряжений (рис. 2):
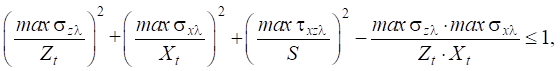(4)
где Zt и Xt — пределы прочности на растяжение в направлениях Z и X; S — предел прочности на сдвиг в плоскости XZ.
Рис. 2. Осредненные на базе l напряжения у вершины трещины:
а — ENF-испытания; б — DCB-испытания
В связи с наличием плоскостей симметрии для ENF-нагружения построили трехмерную модель 1/2 образца с трещиной (рис. 3), для DCB-испытаний — 1/4 образца с трещиной (рис. 4). Расчеты проводили в программе Ansys Workbench (опция «статический прочностной анализ», static structural).
Рис. 3. Конечно-элементная модель 1/2 образца и фрагмент сетки для ENF-испытаний
Рис. 4. Конечно-элементная модель 1/4 образца и фрагмент сетки для DCB-испытаний
При создании сетки конечных элементов задавали параметр lx = 0,75 мм по ширине образца [19] и параметр lz = 0,2 мм по толщине образца, что соответствует толщине модифицированного слоя [20]. Один конечный элемент по толщине слоя задавали в соответствии с теорией слоев (layer wise theory), используемой при оценке прочности слоев в рамках мезомеханики композитов [21]. В ENF-испытаниях общие перемещения в образце намного больше локальных перемещений от нагружающего ролика (рис. 1 б), поэтому в местах приложения нагрузок и опор не делали сгущение сетки конечных элементов (рис. 3). Свойства стеклопластика, использованные в расчете:
- модули упругости Ex= Ey= 23 ГПа, Ez = 9 Гпа;
- модули сдвига Gxy= Gyz= Gxz = 6 000 Гпа;
- коэффициенты Пуассона mxy= 0,15, myz= mxz = 0,3 [22].
Так как объемная доля трансверсального армирования меньше 1 % [16], то в расчетах принимали, что упругие свойства стеклопластика не изменяются при наличии фелтинга.
Зависимость P(d) рассчитали в соответствии с описанной ниже последовательностью.
- Выполнили МКЭ-расчет максимальных напряжений max σzλ, max σxλ и max τxzλ и перемещений d точки приложения нагрузки P= 1 Н для трещин с заданными длинами в диапазоне а = 20–90 мм (DCB) и а = 25–40мм (ENF).
- Методом наименьших квадратов построили аппроксимационные зависимости σzλ=f(a, P) = P ∙ b1 ∙ a; σxλ = f(a, P) = P ∙ b2 ∙ a; τxzλ = f(a, P) = P ∙ b3 ∙ a; d = f(a, P) = P ∙ c1 ∙ a3 ∙ (DCB) и σzλ = f(a, P) = P ∙ b1 ∙ a; σxλ = f(a, P) = P ∙ b2 ∙ a; τxzλ = f(a, P) = P ∙ (b3 ∙ a + d3); d = f(a, P) = P ∙ (c1 ∙ a3 + c2 ∙ a2 + c3 ∙ a + c4) ∙ (ENF).
- Определили нагрузку Pcr(a0) и перемещение dcr, при которых начальная длина трещины a0 скачкообразно увеличится на lx= 0,75 мм при нарушении критерия прочности (4).
- При длине трещины a0+nl определили нагрузки P(a0+nl) и перемещения d(n) для n>
Результаты исследования
Результаты экспериментального определения межслойной трещиностойкости методом ENF. На рис. 5 представлены кривые «нагрузка — перемещение» для всех испытанных образцов. Все кривые «нагрузка — перемещение» имеют область с постоянной податливостью (Clin), соответствующую линейному соотношению «нагрузка — перемещение». Значения Clin использовали для калибровки.
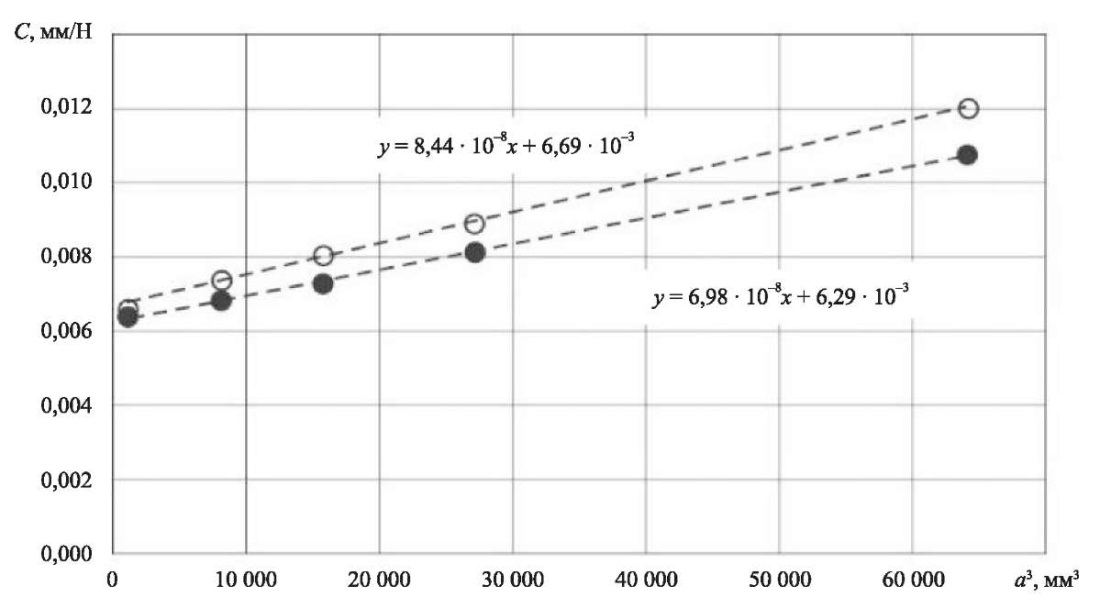
На рис. 6 представлены калибровочные кривые. Для образцов с фелтингом и без фелтинга
податливость пропорциональна кубу длины трещины.
Рис. 6. Зависимость податливости образца C от куба длины трещины a³:
○ — без фелтинга; ● — с фелтингом
Для расчета значений длины трещины a*, соответствующих податливости в начале расслоения C(Pmax), использовали полученные калибровочные кривые и уравнение (2). Для найденных значений длины трещины a* с помощью уравнения (3) вычислили значения GIIс. Результаты приводятся в таблице 1.
Таблица 1
Результаты ENF-испытаний
|
Плотность фелтинга, см–2 |
а0, мм |
Clin, мм/Н |
C(Pmax), мм/Н |
a*, мм |
Pmax, Н |
GIIc, кДж/м2 |
GIIc (среднее значение), кДж/м2 (CV) |
|
0 |
25 |
8,032 |
8,845 |
29,4 |
504,6 |
1,723 |
1,840 ± 0,126 (6,9 %) |
|
0 |
25 |
7,980 |
8,807 |
29,3 |
544,6 |
1,983 |
|
|
0 |
25 |
8,299 |
9,392 |
31,7 |
489,4 |
1,908 |
|
|
0 |
25 |
7,905 |
8,900 |
29,7 |
505,2 |
1,746 |
|
|
10 |
25 |
7,587 |
8,337 |
30,8 |
627,3 |
2,432 |
2,441 ± 0,154 (6,3 %) |
|
10 |
25 |
7,849 |
8,677 |
32,4 |
625,8 |
2,682 |
|
|
10 |
25 |
7,937 |
8,811 |
33,0 |
578,4 |
2,376 |
|
|
10 |
25 |
7,824 |
8,594 |
32,1 |
581,4 |
2,261 |
|
|
10 |
25 |
7,880 |
8,818 |
33,1 |
589,3 |
2,456 |
Примечание: CV — Коэффициент вариации (от англ. сoefficient variation).
Образцы с фелтингом показали значительное (на ~33 %) увеличение межслойной вязкости разрушения GIIс по сравнению с контрольными образцами. После испытаний образцы с фелтингом разделяли острым ножом и рассматривали под микроскопом. Микрофотографии зоны без фелтинга (область начальной трещины) и зоны с фелтингом (область развития трещины) представлены на рис. 7. При развитии трещины разрушаются вытянутые при фелтинге волокна, потому что их длина больше критической [16].
Рис. 7. Микрофотографии образцов с фелтингом после ENF-испытаний:
а — зона без фелтинга (область начальной трещины);
б — зона с фелтингом (область развития трещины);
в — зона с фелтингом (увеличенный масштаб)
Результаты расчета напряженного состояния у вершины трещины при нагружении по схемам
DCB и ENF. На рис. 8, 9 показаны зависимости напряжений max σzλ(a), max σxλ (a), max τxzλ (a) и перемещений d(a). Условия: P = 1 Н, нагружение по схемам DCB и ENF.
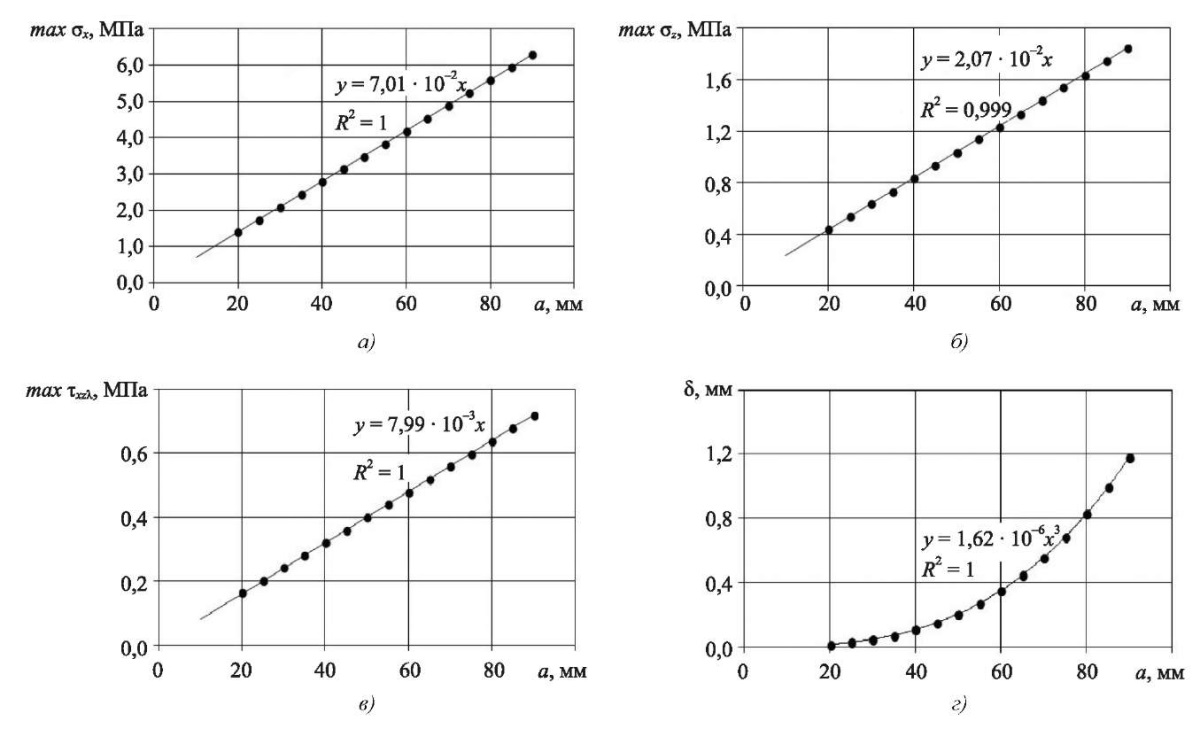
Рис. 8. DCB-нагружение. Зависимости максимальных напряжений и перемещений
от длины трещины при Р = 1 Н:
а — зависимость нормальных напряжений max σxλ(a);
б — зависимость нормальных напряжений max σzλ(a);
в — зависимость касательных напряжений max τxzλ(a);
г — зависимость перемещений d(a)
Рис. 9. ENF-нагружение. Зависимости максимальных напряжений и перемещений
от длины трещины при Р = 1 Н:
а — зависимость нормальных напряжений max σxλ(a);
б — зависимость нормальных напряжений max σzλ(a);
в — зависимость касательных напряжений max τxzλ(a);
г — зависимость перемещений d(a)
Примеры распределения напряжений у вершины трещины представлены на рис. 10, 11 при длине трещины a0 = 30 мм.
Рис. 10. Напряжения у вершины трещины при DCB-нагружении:
а — нормальные напряжения σxλ;
б — нормальные напряжения σzλ;
в — касательные напряжения τxzλ
Рис. 11. Напряжения у вершины трещины при ENF-нагружении:
а — нормальные напряжения σxλ;
б — нормальные напряжения σzλ;
в — касательные напряжения τxzλ
Для получения расчетных зависимостей «нагрузка — перемещение» с помощью МКЭ учитываются характеристики прочности композита в главных направлениях, т.е. критерий (4). Представляет сложность прямое получение трансверсально-сдвиговых констант, поэтому ниже рассмотрен обратный метод. При таком подходе константы варьируются и выясняется их наилучшее сочетание. Это значит, что расчетные и экспериментальные диаграммы нагружения хорошо согласуются (среднеквадратичное отклонение перемещений при заданных нагрузках минимальное).
Результаты расчета при нагружении по схеме DCB сравнивали с экспериментом авторов, который рассмотрен в [16]. Образцы изготовили так же. Испытания провели в соответствии со стандартами ГОСТ Р 56815–20153 и ASTMD5528–144.
Расчет проводили для нагружения по схеме DCB. При расчете зависимости P(d) для образцов без фелтинга нашли и округлили до целых значений следующие величины пределов прочности: Zt = 39 МПа, Xt = 360 МПа, S = 82 МПа. Полученные значения 360 МПа и 39 МПа соответствуют данным по прочности стеклопластиков, указанным в [23]. Для образцов с фелтингом (плотность 10 см–2) в расчетах получили значения Xt* = 270 МПа, Zt* = 46 МПа и S* = 97 МПа. Таким образом, использование фелтинга позволило увеличить предел прочности на растяжение в направлении Z с 39 до 46 МПа (на ~18 %).
При нагружении по схеме DCB пределы прочности на сдвиг в плоскости XZ S и S* не вносят большой вклад в критерий (4), поэтому полученные в расчетах по схеме DCB значения S = 82 МПа и S* = 97 МПа нужно уточнить по схеме нагружения ENF. Отметим, что влияние нормальных напряжений в направлениях X и Z незначительно по сравнению с касательными напряжениями при нагружении по схеме ENF. Поэтому в расчетах при поиске значений S и S* величины Zt, Xt, Zt* и Xt* брали из решения обратной задачи при нагружении по схеме DCB.
Из условия наилучшей согласованности экспериментальных и расчетных кривых P(d) (среднеквадратичное отклонение перемещений при заданных нагрузках минимальное) определили значения S = 77 МПа (без фелтинга) и S* = 89 МПа (с фелтингом). Как видим, фелтинг позволил увеличить предел прочности на сдвиг в плоскости XZ на ~16 %.
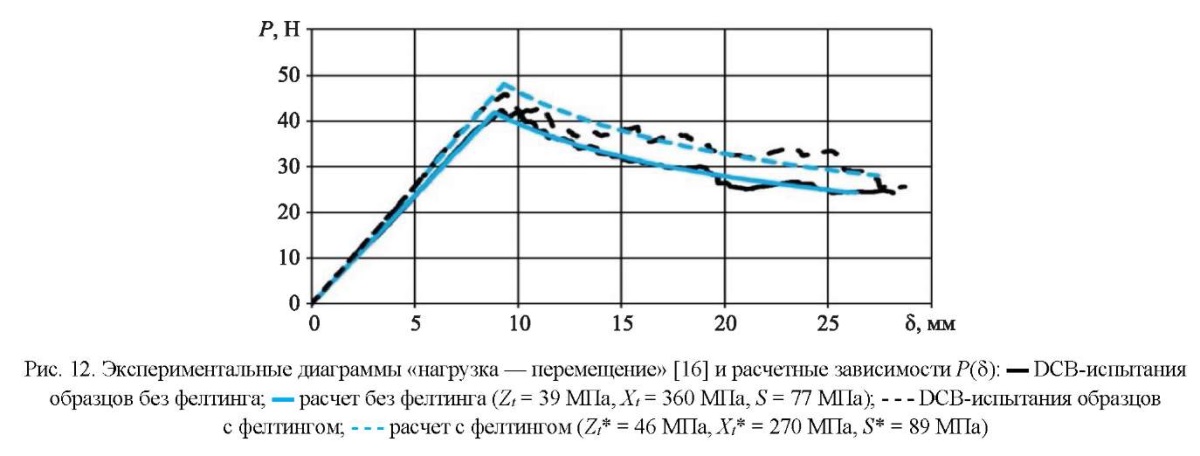
На рис. 12–13 приводятся экспериментальные диаграммы «нагрузка — перемещение», а также расчетные зависимости P(d) при найденных значениях пределов прочности:
- Zt= 39 МПа, Xt= 360 МПа, S = 77 МПа (для контрольных образцов без фелтинга);
- Zt* = 46МПа, Xt* = 270МПа, S* = 89 МПа (для образцов с фелтингом).
Обсуждение и заключение. Исследования тканевого композита показали, что фелтинг плотностью 10 см–2 увеличивает вязкость межслойного разрушения GIIc на ~33 %.
С помощью МКЭ проанализировали напряженное состояние в квазистатической упругой постановке задачи и с использованием нелокальной теории прочности для разработанных численных моделей балки с трещинами известной длины. Особенностью расчетов было то, что в них не использовали контактные алгоритмы, а рассматривали лишь разрушение слоя композита, ближайшего к трещине, и соответствующее изменение площади склейки слоев. То есть трещина рассматривалась как концентратор напряжений. Критерий прочности композита, содержащий три параметра и записанный через осредненные напряжения, позволяет использовать метод пошагового продвижения трещины для прогнозирования кривой «нагрузка — перемещение».
Использование фелтинга плотностью 10 см–2 увеличивает предел прочности на растяжение композита в направлении Z на ~18 %, а предел прочности на сдвиг в плоскости XZ — на ~16 %. Это стало известно из решения обратной задачи, т.е. поиска характеристик прочности материала по критерию (4) и кривой «нагрузка — перемещение».
Итоги представленного исследования найдут свое практическое применение. В частности, их можно использовать в задачах прогнозирования дефектов типа расслоений (например, при низкоскоростных ударах по композитам в обшивках летательных аппаратов). Результаты данной научной работы будут полезны для устранения указанных дефектов с помощью фелтинга.
1. ASTM D7905/D7905M–14. Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. URL: https://cdn.standards.iteh.ai/samples/89096/03be6b5e53664f13a87л03bb4342d981a/ASTM-D7905-D7905M-14.pdf (дата обращения: 22.04.2024).
2. ГОСТ 33685–2015. Композиты полимерные. Метод определения удельной работы расслоения в условиях сдвига. URL: https://docs.cntd.ru/document/1200127774 (дата обращения: 22.04.2024).
3. ГОСТ Р 56815–2015. Композиты полимерные. Метод определения удельной работы расслоения в условиях отрыва. URL: https://docs.cntd.ru/document/1200131393/titles (дата обращения 22.04.2024).
4. ASTM D5528M–21. Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. https://doi.org/10.1520/D5528_D5528M-21
Список литературы
1. Callister WD Jr., Rethwisch DG. Materials Science and Engineering: An Introduction. 10th edn. Hoboken, NJ: Wiley; 2018. 992 p. URL: https://www.wiley.com/en-us/Materials+Science+and+Engineering%3A+An+Introduction%2C+10th+Edition-p9781119405498 (accessed: 22.04.2024).
2. Wei Tan, Falzon BG, Chiu LNS, Price M. Predicting Low Velocity Impact Damage and Compression-After-Impact (CAI) Behaviour of Composite Laminates. Composites Part A: Applied Science and Manufacturing. 2015;71:212–226. https://doi.org/10.1016/j.compositesa.2015.01.025
3. Balasubramani Veerappan, S Rajendra Boopathy. Prediction of Residual Tensile Strength of Laminated Composite Plates after Low Velocity Impact. ARPN Journal of Engineering and Applied Sciences. 2014;9(3):320–325.
4. Abrate S. Impact on Composite Structures. Cambridge: Cambridge University Press; 2009. 289 p. https://doi.org/10.1017/CBO9780511574504
5. Liyong Tong, Mouritz AP, Bannister MK. 3D Fibre Reinforced Polymer Composites. Amsterdam: Elsevier Science; 2002. 254 p. https://doi.org/10.1016/B978-0-08-043938-9.X5012-1
6. Jinlian Hu. 3-D Fibrous Assemblies: Properties, Applications and Modeling of Three-Dimensional Textile Structures. Sawston, Cambridge: Woodhead Publishing; 2008. 280 p.
7. Chen Xiaoming, Zhao Yufen, Zhang Chunyan, Wang Xiaoxu, Chen Li. Robot Needle-Punching for Manufacturing Composite Performs. Robotics and Computer-Integrated Manufacturing. 2018;50:132–139. https://doi.org/10.1016/j.rcim.2017.09.008
8. Forental GA, Kheruvimov AV, Nikonov AV, Sapozhnikov SB. Stack Fabric Felting to Get PCM Gllc Improvement and LVI Tolerance. IOP Conference Series: Materials Science and Engineering. 2021;1024(1):012001. https://doi.org/10.1088/1757-899X/1024/1/012001
9. Sham MS, Venkatesha CS, Jayaraju T. Experimental Methods of Determining Fracture Toughness of Fiber Reinforced Polymer Composites under Various Loading Conditions. Journal of Minerals and Materials Characterization and Engineering. 2011;10(13):1263–1275. http://doi.org/10.4236/jmmce.2011.1013099
10. Pinho S, Robinson P, Iannucci L. Developing a Four Point Bend Specimen to Measure the Mode I Intralaminar Fracture Toughness of Unidirectional Laminated Composites. Composites Science and Technology. 2009;69(7–8): 1303–1309. https://doi.org/10.1016/j.compscitech.2009.03.007
11. Issam Tawk, Jihad Rishmany, Nicolas Saba, Pablo Navarro, Jean-Francois Ferrero. Experimental Study of the Interlaminar Fracture of Composite Materials in Mode III by MSCB Test. Composite Structures. 2020;233:111548. https://doi.org/10.1016/j.compstruct.2019.111548
12. Hossein Saidpour, Mehdi Barikani, Multu Sezen. Mode-II Interlaminar Fracture Toughness of Carbon/Epoxy Laminates. Iranian Polymer Journal. 2003;12(5):389–400.
13. Sham Prasad MS, Venkatesha CS, Jayaraju T. Experimental Methods of Determining Fracture Toughness of Fiber Reinforced Polymer Composites under Various Loading Conditions. Journal of Minerals and Materials Characterization and Engineering. 2011;10(13):1263–1275. http://doi.org/10.4236/jmmce.2011.1013099
14. Ying Zeng, Hong-Yuan Liu, Yiu-Wing Mai, Xu-Sheng Du. Improving Interlaminar Fracture Toughness of Carbon Fibre/Epoxy Laminates by Incorporation of Nano-Particles. Composites Part B: Engineering. 2012;43(1):90–94. https://doi.org/10.1016/j.compositesb.2011.04.036
15. Kadhum A, Muslim ZR, Jaffer HI. Interlaminar Fracture of Micro and Nano Composites Special. Acta Physica Polonica: Series A. 2019;135(5):1126–1128. http://doi.org/10.12693/APhysPolA.135.1126
16. Форенталь Г.А., Сапожников С.Б. Перспективы технологии фелтинга для локального трехмерного армирования полимерных тканевых композитов. Композиты и наноструктуры. 2022;14(4):233–245. https://doi.org/10.36236/1999-7590-2022-14-4-233-245233
17. Maimi P, Gonzalez EV, Gascons N, Ripoll L. Size Effect Law and Critical Distance Theories to Predict the Nominal Strength of Quasibrittle Structures. Applied Mechanics Reviews. 2013;65(2):020803. https://doi.org/10.1115/1.4024163
18. Hoang Thai Nguyen, A Abdullah Dönmez, Zdenek P Bazant. Structural Strength Scaling Law for Fracture of Plastic-Hardening Metals and Testing of Fracture Properties. Extreme Mechanics Letters. 2021;43(1):101141. https://doi.org/10.1016/j.eml.2020.101141
19. Taylor D. The Theory of Critical Distances: A New Perspective in Fracture Mechanics. Amsterdam: Elsevier Science; 2007. 306 p. https://doi.org/10.1016/B978-0-08-044478-9.X5000-5
20. Mahmoodi MJ, Khamehchi M. Finite Element Analysis of Free Corner Effects in Composite Laminates Based on a Global–Local Model. Archive of Applied Mechanics. 2023;93(12):4327–4350. http://doi.org/10.1007/s00419-023-02494-1
21. Jaehong Lee, Zafer Gurdal, O Hayden Griffin Jr. Layer-Wise Approach for the Bifurcation Problem in Laminated Composites with Delaminations. AIAA Journal. 1993;31(2):331–338. https://doi.org/10.2514/3.11672
22. Сапожников С.Б. Разрушение тканевых композитов с концентраторами напряжений: учет неупругого деформирования в численном моделировании. Композиты и наноструктуры. 2020;2(46):31–39. https://doi.org/10.36236/1999-7590-2020-12-2-31-39
23. Barbero EJ. Introduction to Composite Materials Design, 2nd ed. Boca Raton: CRC Press; 2011. 562 p. https://doi.org/10.1201/9781439894132
Об авторах
Г. А. Форенталь
Южно-Уральский государственный университет
Россия
Россия
Галина Анатольевна Форенталь, инженер-исследователь
454080, г. Челябинск, пр. Ленина, 76
С. Б. Сапожников
Южно-Уральский государственный университет; Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского
Россия
Россия
Сергей Борисович Сапожников, доктор технических наук, профессор; ведущий ученый
454080, г. Челябинск, пр. Ленина, 76
140180, г. Жуковский, Московская область, ул. Жуковского, 1
Рецензия
Для цитирования:
Форенталь Г.А., Сапожников С.Б. Повышение межслойной трещиностойкости полимерных тканевых композитов с помощью локального трехмерного армирования (фелтинга). Advanced Engineering Research (Rostov-on-Don). 2024;24(3):215-226. https://doi.org/10.23947/2687-1653-2024-24-3-215-226. EDN: KVEMQM
For citation:
Forental G.А., Sapozhnikov S.B. Increasing the Interlayer Fracture Toughness of Polymer Fabric Composites Using Local 3D-Reinforcement (Felting). Advanced Engineering Research (Rostov-on-Don). 2024;24(3):215-226. https://doi.org/10.23947/2687-1653-2024-24-3-215-226. EDN: KVEMQM
Просмотров:
627
Послать статью по эл. почте 