Scroll to:
Determination of Dynamic Stresses and Displacements under the Action of an Impact Load on a Two-Layer Structure during the Indentation Process
https://doi.org/10.23947/2687-1653-2024-24-3-264-273
EDN: VVRPYB
Abstract
Introduction. Numerous researchers of the reliability of building structures pay attention to hardness, an important characteristic of the structural material. It is determined by indentation — pressing the tip of the tool into the surface. The advantages of dynamic indentation methods and the distribution of stress intensity on the surface and inside the sample are investigated. However, the condition of layered materials on impact has been poorly studied. The objective of the presented work is to consider indentation for a two-layer sample and determine the sensitivity of the top layer to the strength of the substrate. This will allow us to identify significant characteristics of the strength properties of homogeneous and heterogeneous structures.
Materials and Methods. An elastoplastic model of material behavior and a shock indentation scheme were used, which took into account the masses of the indenter and the striker coupled by linear springs. The surface of the indenter was conical, the opening angle was 120°. The impact was simulated in the MATLAB system. Finite element model in Ansys APDL was used to verify the data and analyze the results of the experiment. Traditional models of elasticity theory were used for calculations. The behavior of the material in the zone of plastic deformation was described using the options of multilinear isotropic hardening and the von Mises plasticity criterion.
Results. The results of comparing three versions of varying the level of yield strength in the bottom layer are presented: when the yield strength in the bottom layer is half as high as the top one, equal to it, and twice as high. Displacements at different observation points for samples with a top layer of 2 mm and 1 mm were analyzed. In the first case, under horizontal shear, the displacement indices inside the sample did not change if the yield strength level was twice lower or higher than in the top one. If these indicators were equal, the difference became noticeable. In the second case (layer 1 mm), the difference in displacement was visible at all observation points. Thus, it can be reasonably concluded that a structure with a smaller top layer is more sensitive to impact. In the course of the research, it became known that vibrations associated with the transition to the plasticity zone occurred in the 2 mm zone, and elastic damping vibrations occurred below this zone. We solved the classification problem for the top layer of the material with changing characteristics of the base. The indicator for comparison was the Brinell hardness (HB) in the range of 200–600. The results were processed using a neural network and visualized in the form of graphs. The accuracy of its calculations was 98%.
Discussion and Conclusion. To determine the strength properties of homogeneous structures, it is sufficient to characterize the speed of displacement inside the sample. For an inhomogeneous structure, additional parameters should be introduced — displacements on the surface and inside the sample at fixed observation points. An integrated approach to determining the strength properties of an inhomogeneous structure improves the accuracy of calculations, and the use of neural networks increases their speed.
Keywords
For citations:
Babushkina N.E., Lyapin A.A. Determination of Dynamic Stresses and Displacements under the Action of an Impact Load on a Two-Layer Structure during the Indentation Process. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):264-273. https://doi.org/10.23947/2687-1653-2024-24-3-264-273. EDN: VVRPYB
Introduction. When designing and operating building structures, strict requirements are specified to their strength and reliability [1]. The literature discusses the issues of reliability of the structure [2], as well as the preservation of its operational properties throughout its entire service life [3].
From an engineering point of view, hardness is one of the important material specifications. It is associated with mechanical properties, such as yield strength, tensile strength, endurance, etc. Hardness of the material is determined by pressing the tip of the tool into the surface. There is a distinction between static and dynamic indentation. The static indentation test involves the indentation of a solid indenter into a flat and smooth surface of a soft material (target), whose mechanical properties are determined by the measured dependence of the applied load on the depth of penetration. Static methods do not allow us to evaluate the physicomathematical characteristics of the material under dynamic loading conditions [4]. Dynamic indentation methods are used for this purpose [5].
GOST R 56474–20151 presents dynamic indentation as the introduction of an indenter into material under the action of a single shock pulse created by a special acceleration device or gravity. This approach applies to non-destructive testing methods. Their basic principle is safe inspection, determination of the integrity, and basic working properties of the object [6]. The primary advantage is the ease of use.
Indentation testing is a complex process that includes contact mechanics, material nonlinearity, and fracture mechanics. For general cases, it is very difficult to obtain analytical solutions. Therefore, the understanding of the processes under consideration is based mainly on experiments and finite element modeling.
Elastic contact was first studied by G. Hertz [7] at the end of the XIX century. He tried to find an accurate definition of hardness using an elastic process. Later, J.V. Boussinesq developed a method based on potential theory for calculating stresses and displacements in an elastic body loaded with any rigid axisymmetric indenter. As for the depressions associated with plastic deformation, early research focused on yield strength and tensile strength.
Publications pay attention to the methods of dynamic indentation to determine the strength properties of structures. Thus, N.N. Avtonomov and A.V. Tololo considered the problem of pressing a spherical indenter into an elastoplastic material [8]. The authors analyzed the distribution of stress intensity on the surface and inside the sample. Thus, it became known that the zones of maximum intensity are located at a short distance from the contact zone of the indenter and the sample, and expand with increasing load.
Foreign authors [9] have developed a method of dynamic indentation, which consists in measuring the depth and reaction to the load of the sample during the indentation process. To determine the depth, a displacement measurement method based on moire interferometry was used. The load was measured with a quartz sensor. The results of numerical simulation by the finite element method indicated that this approach was in good agreement with the values obtained using traditional methods for determining the strain rate.
Scientists considered strength properties of materials in the indentation process. Many papers are devoted to this, for example [10]. The study of the behavior of the “target” under the mechanical loads plays a key role in the development of new materials, structures and products [11]. Comprehensive research makes it possible to solve the problems of optimizing operating procedures, providing the reliability of structures, and preventing failures in their operation.
The solutions obtained open up the possibility of creating more efficient and sustainable structures [12], which determines the relevance of research in this direction. At the same time, the issue of the state of layered structures under impact is still insufficiently studied.
The work is aimed at analyzing stresses and displacements in a two-layer structure and identifying the sensitivity level of the top layer of the sample to the strength of the substrate. The study will allow us to establish significant characteristics for determining the strength properties of homogeneous and heterogeneous structures.
Materials and Methods. The diagram of the impact indentation device is shown in Figure 1.
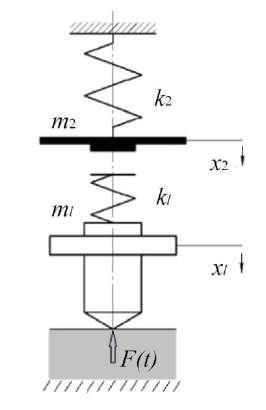
Fig. 1. Diagram of the impact indentation device
The system of differential equations corresponding to the dynamics of the mechanical elements of the shock indentation device has the form:
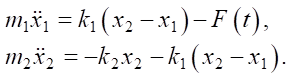 (1)
(1)
This is how the oscillatory process of a dynamic system with two masses is described: m1 — mass of the indenter;
m2 — mass of the striker. The masses are coupled by linear springs with stiffness k1 and k2, respectively [13]. The values of vertical displacements x1(t), x2(t) as degrees of freedom of massive elements are unknown in time. The striker was cocked to height h After descending, at the moment of contact with the indenter, he reached the speed
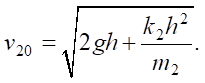
Thus, the initial conditions should be added to the system (1):
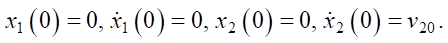 (2)
(2)
Value F(t) of the resistance force from the injected material is unknown.
We assume that the surface of the indenter is conical with opening angle α = 120 degrees. Therefore, it is required to use an elastic-plastic model of the behavior of the test material. At the apex of the cone, the onset of impact and plastic deformation coincides.
The impact process was modeled in the MATLAB system. This made it possible to select the mechanical parameters of the installation. A finite element model in the Ansys APDL environment was used to verify the data and analyze the results of the experiment. A two-layer construction was considered. Its displacements and stresses arising in a two-layer sample under the action of a dynamic load were analyzed. Traditional models of elasticity theory were used in the calculations. To describe the behavior of the material in the zone of plastic deformation, the options of multilinear isotropic hardening and the von Mises plasticity criterion were used:
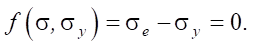 (3)
(3)
where σe — von Mises equivalent stress,
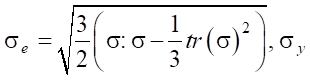 — uniaxial yield strength.
— uniaxial yield strength.
To control the convergence accuracy, a finite element grid was pre-selected. When studying the parameters of a two-layer structure, we considered three options for varying the level of yield strength in the bottom layer in three cases — when the yield strength in the bottom layer is half as high as the top one, equal to it, and twice as high (Table 1).
Table 1
Structure and Parameters of the Studied Structures
|
No. |
Level of yield strength in the bottom layer |
Level, mm |
|
|
top |
bottom |
||
|
1 |
1/2 |
1 |
9 |
|
2 |
1 |
||
|
3 |
2 |
||
|
4 |
1/2 |
2 |
8 |
|
5 |
1 |
||
|
6 |
2 |
||
A detailed analysis of the displacements at different observation points clearly shows the difference in the nature of displacements in the zone of plastic deformations. To study the displacements, the following scheme was selected (Fig. 2). The top layer of the structure was highlighted in a darker gray color for clarity.

Fig. 2. Determination of points for measuring vertical and horizontal displacements:
a — construction with a top layer of 1 mm;
b — construction with a top layer of 2 mm.
Numbers 1, 3 and 5 indicate the level of yield strength in the bottom layer
relative to the top one in accordance with Table 1
Research Results. Figure 3 shows a comparative characteristic of the displacement level on the sample surface with a horizontal shear of the observation point from the impact point.
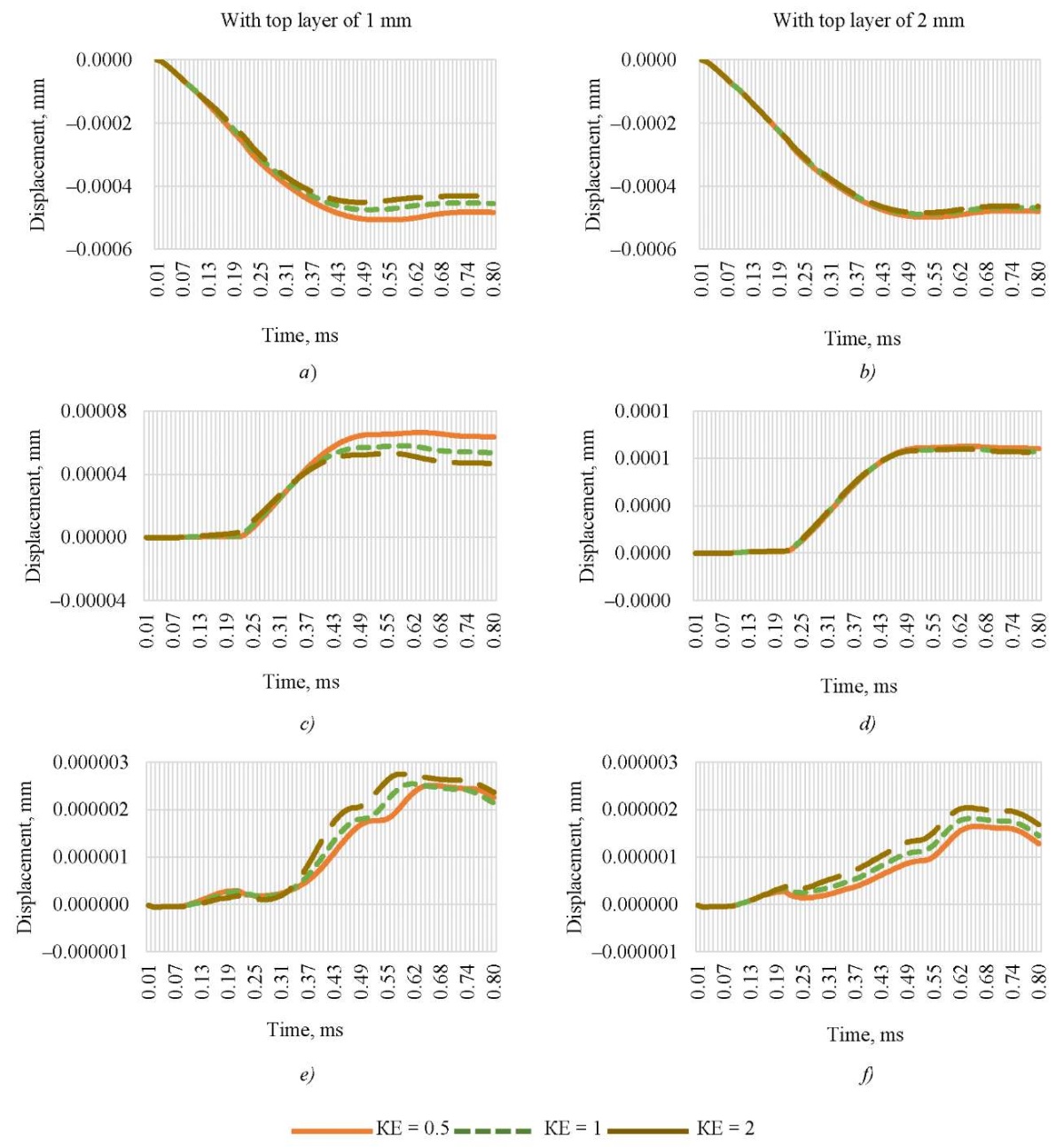
Fig. 3. Displacements on the sample surface at various contact points:
a, b — at the 1st contact point;
c, d — at the 3rd point on the surface;
e, f, — at the 5th point on the surface
Evidently, for a two-layer structure with a top layer of 2 mm, a change in the yield level at the 1st and 3rd contact points during horizontal shear does not affect the displacement parameters inside the sample. At the 5th point, the difference becomes noticeable. For a structure with a top layer of 1 mm, the difference in the level of displacement is noticeable at all observation points. It can be concluded that a structure with a smaller top layer is more sensitive to impact.
Figure 4 shows the distribution of stress intensity at different levels of the top coating. These data suggest that fluctuations associated with the transition to the plasticity zone occur in the 2 mm zone, and elastic vibrations that fade over time occur below this zone.
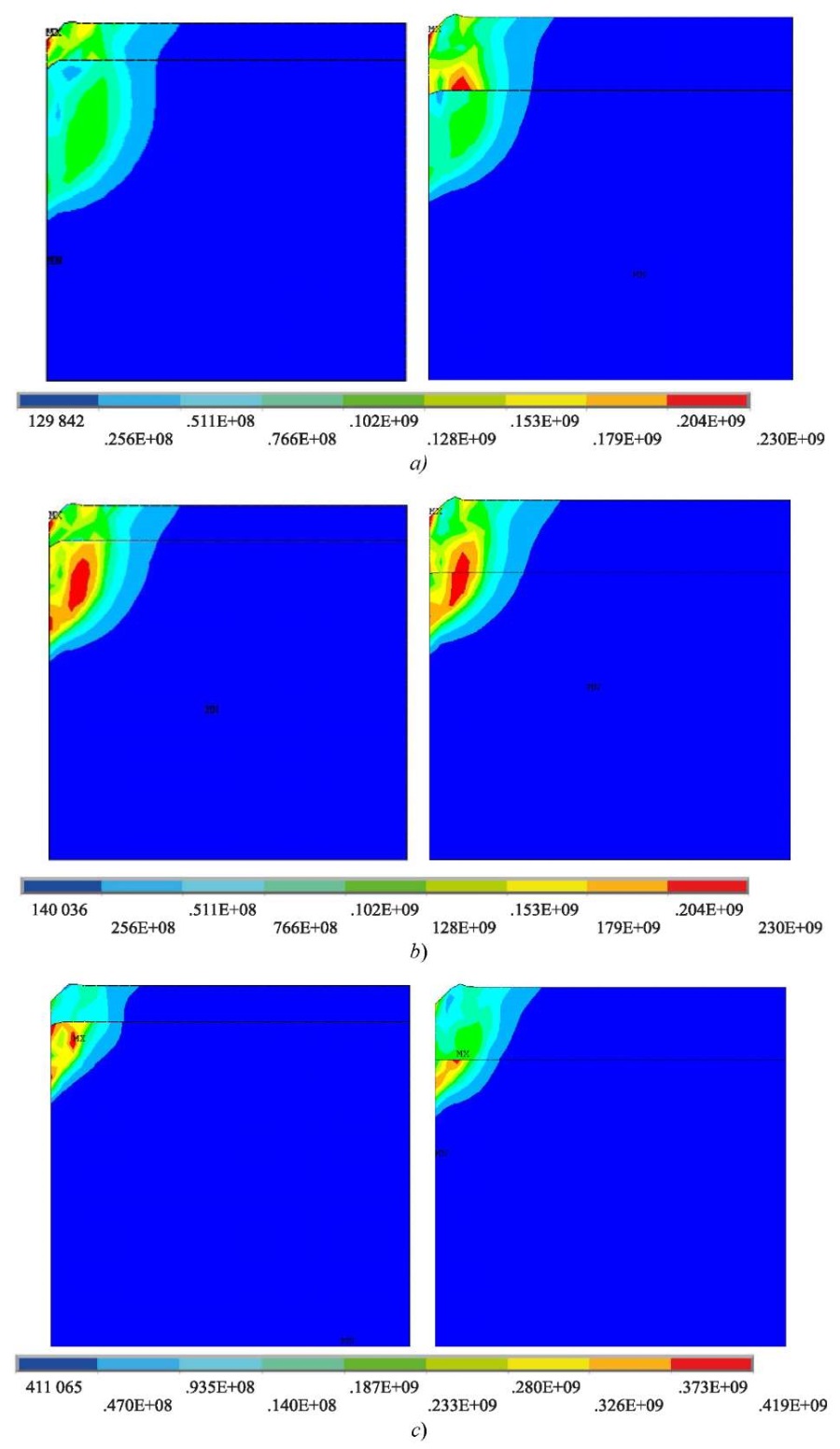
Fig. 4. Stress intensity at different values of strength coefficient K, MPa:
a — К = 0.5; b — К = 1; c— К = 2
Figure 5 shows graphs of stresses on the surface at various observation points.
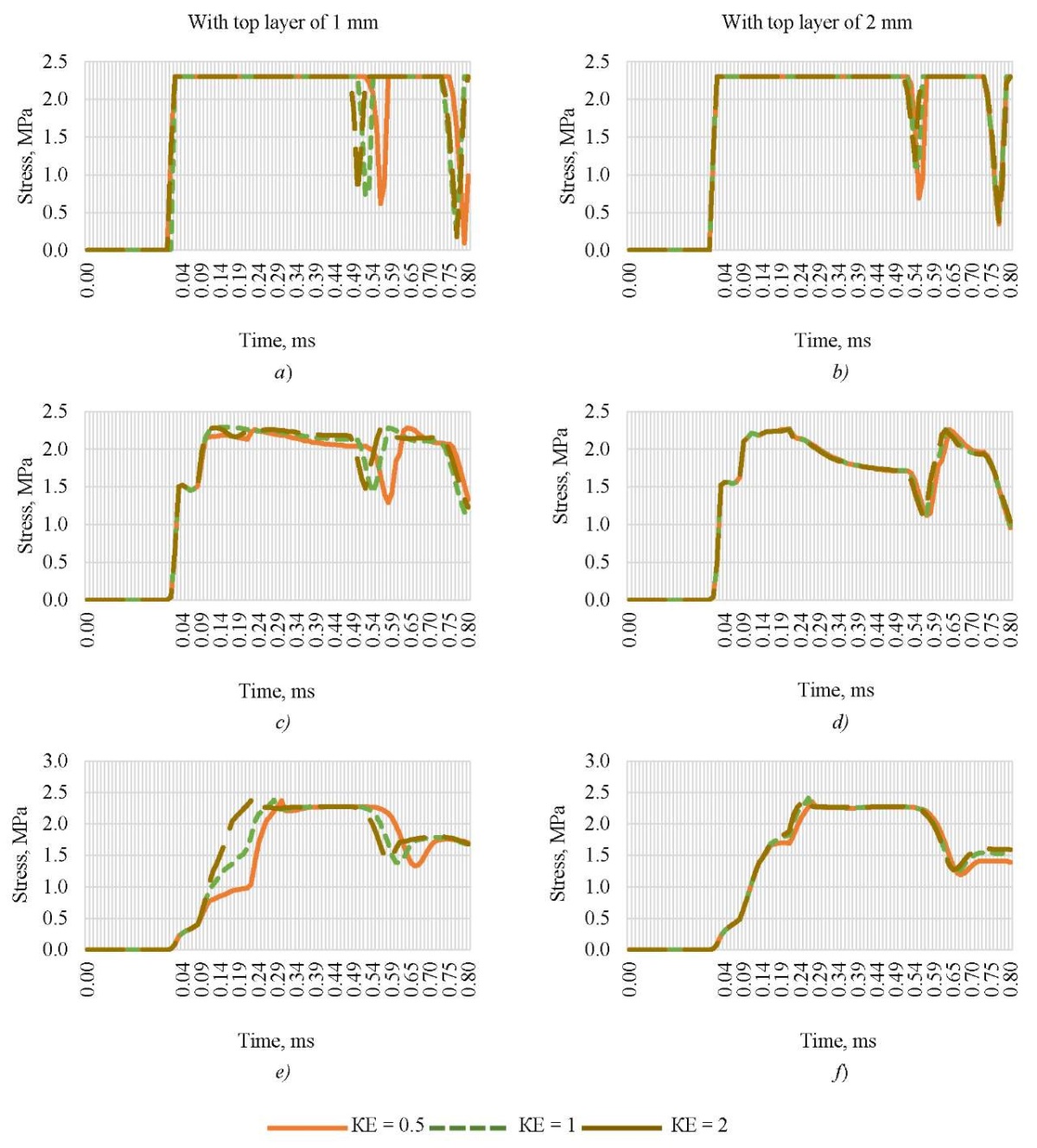
Fig. 5. Stresses on the sample surface at various contact points:
a, b — at the contact point;
c, d — at the 3rd point on the surface;
e, f, — at the 5th point on the surface
To analyze the influence of the base on the strength properties of the sample, the problem of classification [13] by the value of Brinell hardness (HB) of the top layer of the material with varying characteristics of the base was solved. Within the framework of the study, five classification groups were identified (Table 2).
Table 2
Classification Groups
|
No. |
Group |
Value of HB |
|
1 |
I |
200 |
|
2 |
II |
300 |
|
3 |
III |
400 |
|
4 |
IV |
500 |
|
5 |
V |
600 |
The calculated values obtained using a mathematical model were fed to the input of a neural network. Figure 6 shows the values of speeds and displacements for the selected hardness groups.
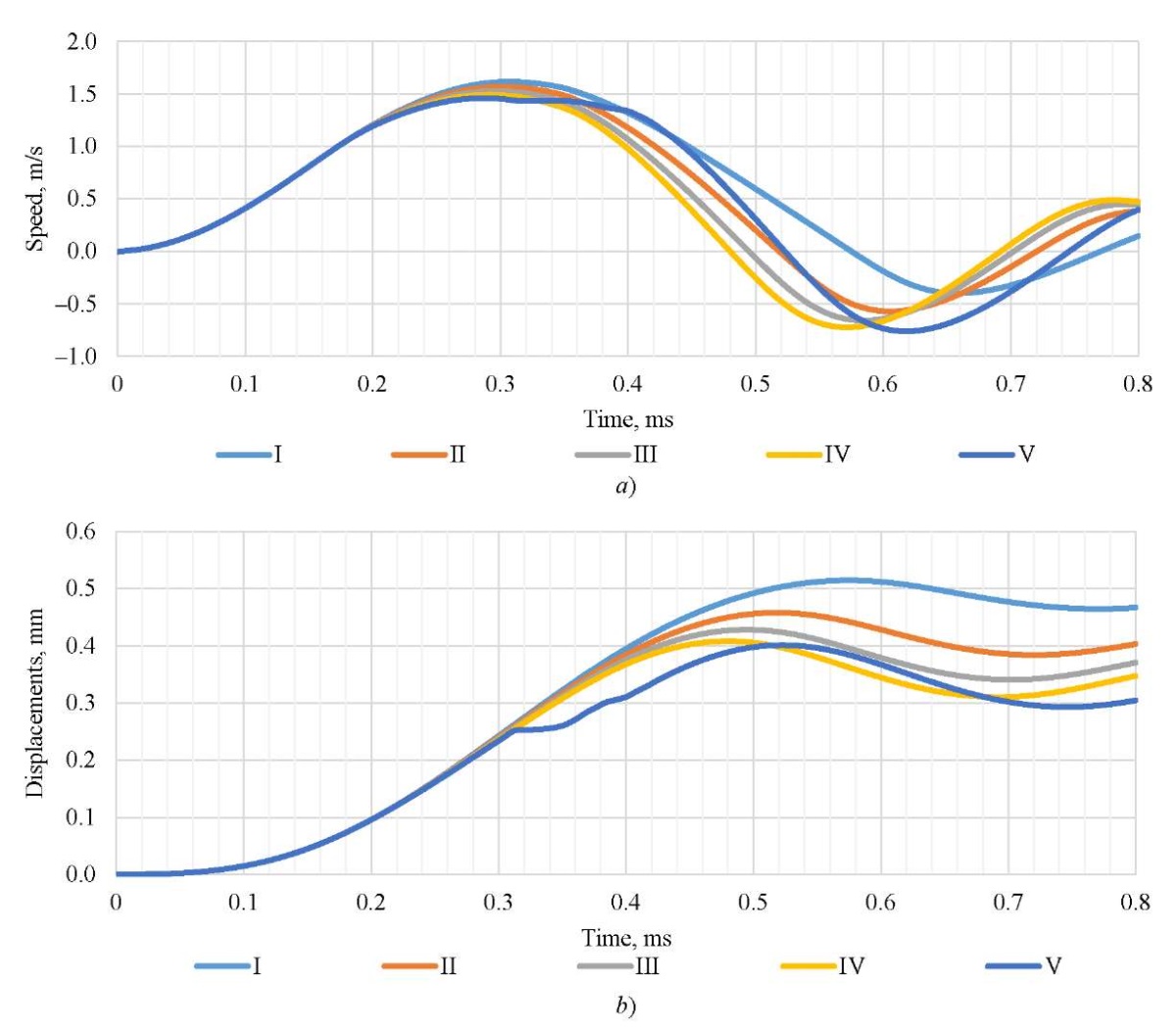
Fig 6. Calculated values for classification groups:
a — rate of indenter introduction; b — displacements
For further data processing, a created and trained neural network with a fully-connected structure was used [14]. It is worth noting that neural networks have extensive capabilities in solving this type of tasks [15], in particular, in the sphere of construction [16]. Neural networks are often used for qualitative assessment, forecasting and monitoring of the condition of building structures [17], as well as for parametric identification of objects [18]. The increase in computing power of neural networks directly affects the development of their functionality [19].
The accuracy of neural network calculations was 98%. Therefore, the neural network correctly analyzes the experimental data and is able to adequately take into account the behavior of the material under shock loading.
Discussion and Conclusion. Thus, the analysis of the distribution of displacements and stresses in the sample allows us to draw a number of conclusions.
- Level of vertical displacements in the wave process is much higher than in the horizontal one.
- Level of stiffness of the substrate affects the distribution of displacements and stresses.
- In the more solid bottom layer, the displacement is noticeably less than in the soft one.
- Top layer is sensitive to the strength of the substrate if its height does not exceed 1 mm.
- With distance from the indentation site, the deformations become elastic, the stress does not go out into the zone of plastic deformations.
Based on the research results, it can be argued that to determine the strength properties of homogeneous structures, one value characterizing the speed of displacement inside the sample is sufficient. For an inhomogeneous structure, it is required to introduce additional parameters, such as displacements on the surface and inside the sample at fixed observation points. An integrated approach to determining the strength properties of an inhomogeneous structure will improve the accuracy of calculations. And the use of neural network technologies to solve this type of problem opens up the possibility of faster calculations.
1. GOST R 56474–2015. Space Systems. Non-destructive Testing of Physical and Mechanical Properties of Space Technique's Materials and Coatings by Dynamic Indentation. General Requirements. Electronic Fund of Legal and Regulatory Documents. URL: https://docs.cntd.ru/document/1200122009 (accessed: 14.05.2024).
References
1. Lyapin A, Beskopylny A, Meskhi B. Structural Monitoring of Underground Structures in Multi-Layer Media by Dynamic Methods. Sensors. 2020;20(18):5241. https://doi.org/10.3390/s20185241
2. Chesnokov AV, Mikhailov VV, Dolmatov IV. Damage Detection in the Soft Shell of the Fabric Roof Construction of Buildings by means of Artificial Neural Network. Structural Mechanics and Structures. 2022;33(2):98–109.
3. Kuklina MV, Leber AI, Makhakova AM. The Use of Neural Network Technology in a Construction Organization. Bulletin of the Altai Academy of Economics and Law. 2022;(5–3):362–368. https://doi.org/10.17513/vaael.2219
4. Kuzmichev MV, Egorov RA. Modeling and Algorithmic Provision of Dynamic Indentation Process. Scientific and Technical Journal of Information Technologies, Mechanics and Optics. 2018;18(5):794–800. https://doi.org/10.17586/2226-1494-2018-18-5-794-800
5. Matlin MM, Kazankin VA, Kazankina EN. Prediction of the Technical Condition of Parts by Indenting in Different Loading Conditions. Herald of Tver State University. Series: Technical Sciences. 2022;13(1):22–27.
6. Rudnitsky VA, Kren AP, Lantsman GA. Evaluation of Metallic Materials Plasticity by Dynamic Indentation Method. Litiyo i Metallurgiya = Foundry Production and Metallurgy. 2017;(2):81-87. (In Russ.) https://doi.org/10.21122/16836065-2017-2-81-87
7. Oliver WC, Pharr GM. An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. Journal of Materials Research. 1992;7:1564–1583. http://doi.org/10.1557/JMR.1992.1564
8. Avtonomov NN, Tololo AV. Exploration of the Stress Distribution in the Specimen during Indentation of the Indenter Ball. Actual Problems of Aviation and Cosmonautics. 2018;14(1):245–247.
9. Jun Lu, Subra Suresh, Guruswami Ravichandran. Dynamic Indentation for Determining the Strain Rate Sensitivity of Metals. Journal of the Mechanics and Physics of Solids. 2003;51(11–12):1923–1938. https://doi.org/10.1016/j.jmps.2003.09.007
10. Matyunin VM, Nuha Abusaif, Marchenkov AYu. Analysis of the Indentation Size Effect on the Hardness Measurements of Materials. Journal of Physics: Conference Series. 2019;1399(4):044016. https://doi.org/10.1088/17426596/1399/4/044016
11. Varghese J, Radig GF, Herkommer D, Dasgupta A. Hybrid Experimental and Computational Approach for Rate Dependent Mechanical Properties Using Indentation Techniques. In: EuroSimE 2005. Proc. 6th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Micro-Electronics and Micro-Systems. New York City: IEEE; 2005. P. 510–514. https://doi.org/510-514.10.1109/ESIME.2005.1502858
12. Kubenko V. Nonstationary Displacements in an Axisymmetric Problem for an Elastic Half-Space Under Mixed Boundary Conditions. International Applied Mechanics. 2021;57:148–159. https://doi.org/10.1007/s10778-021-01069-3
13. Beskopylny AN, Veremeenko AA, Kopylov FS, Krymskiy VS. The Problem for Static Conical Indentation into the Surface Hardened Area. Engineering Journal of Don. 2018;49(2):214–218.
14. Zesheng Lin, Hongxia Ye, Bin Zhan, Xiaofeng Huang. An Efficient Network for Surface Defect Detection. Applied Sciences. 2020;10(17):6085. https://doi.org/10.3390/app10176085
15. Babushkina N, Lyapin A, Kovaleva A. Analysis of Neural Network Results Based on Experimental Data during Indentation. In: Topical Problems of Agriculture, Civil and Environmental Engineering. E3S Web of Conferences (TPACEE). 2020;224:01018. https://doi.org/10.1051/e3sconf/202022401018
16. Elfaki AO, Alatawi S, Abushandi E. Using Intelligent Techniques in Construction Project Cost Estimation: 10-Year Survey. Advances in Civil Engineering. 2014;2014:107926. https://doi.org/10.1155/2014/107926
17. Patel DA, Jha KN. Evaluation of Construction Projects Based on the Safe Work Behavior of Co-employees through a Neural Network Model. Safety Science. 2016;89:240–248. https://doi.org/10.1016/J.SSCI.2016.06.020
18. Poroshin IE, Titov MA. Using Artificial Neural Networks for Parametric Identification of Objects. Young Scientist. 2020;316(26):39–42. (In Russ.)
19. Alfer'ev DA. Usage of Artificial Neural Networks in Modern Society. Social Area. 2020;6(3):6. https://doi.org/10.15838/sa.2020.3.25.6
About the Authors
N. E. BabushkinaRussian Federation
Natalia E. Babushkina, Teaching assistant of the Computer Engineering and Programming Department
1, Gagarin sq., Rostov-on-Don, 344003
A. A. Lyapin
Russian Federation
Alexandr A. Lyapin, Dr.Sci. (Phys.-Math. ), Professor, Head of the Information Systems in Construction Department
1, Gagarin sq., Rostov-on-Don, 344003
Review
For citations:
Babushkina N.E., Lyapin A.A. Determination of Dynamic Stresses and Displacements under the Action of an Impact Load on a Two-Layer Structure during the Indentation Process. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):264-273. https://doi.org/10.23947/2687-1653-2024-24-3-264-273. EDN: VVRPYB
JATS XML














































