Оптимизационная задача для вероятностных временны́х интервалов квазидетерминированного выходного и самоподобного входного потока пакетов данных в телекоммуникационных сетях

Введение. Телекоммуникационные сети работают в условиях увеличивающихся нагрузок и роста трафика, который подчиняется сложным вероятностным законам распределения и не поддается точному прогнозированию. Самоподобие потока пакетов создает устойчивые зависимости, что ограничивает объем информационного обмена пользователей [1]. В [2] предложены методы, обеспечивающие удовлетворение требований к качеству обслуживания (англ. quality of service, QoS) передачи и приема информации. Авторы указанной работы полагают, что необходимо фокусироваться на приоритетном трафике сетей нового поколения, однако их решение не устраняет проблему самоподобия потоков пакетов. Милан Г. предложил модель управления сетевыми потоками с учетом пропускной способности каналов, не принимая во внимание фрактальные характеристики трафика [3]. В [4] разработаны методы балансировки нагрузки с учетом мультифрактальных свойств трафика, однако они не решают проблемы самоподобия и структурной оптимизации выходных потоков. Ушанев К.В. и Макаренко С.И. [5], проанализировав методы повышения устойчивости сетей с учетом сложных характеристик трафика, предложили модели трансформации самоподобных входных потоков [6]. В данном случае строгий математический анализ позволил бы минимизировать отличия между распределениями входных и выходных потоков и, следовательно, устранить самоподобие. Однако в [6] такое решение отсутствует.

Качественная регулярная передача данных предполагает использование модели источника трафика с постоянной скоростью (постоянный битрейт, англ. constant bitrate, CBR) [4]. В этой модели узел передает пакеты фиксированного размера через равные интервалы времени T. Если время между отправкой пакетов значительно больше времени передачи одного пакета, то размер пакета может быть несущественным. Как отмечается в [4], в условиях ограниченной пропускной способности данную модель можно использовать для обеспечения стационарности трафика и минимизации задержек. В [7] показаны преимущества CBR для сетей с жесткими требованиями к временны́м характеристикам передачи, а в [8] подчеркивается ее эффективность в условиях высокой плотности сенсоров. Согласно [9], предсказуемость трафика в указанной модели делает ее более результативной с точки зрения экономии энергии, что критично для энергетически ограниченных устройств.

Как показано в [10], модель CBR традиционно ассоциируется с беспроводными сенсорными сетями, однако она также может быть полезной в сетях общего назначения [11]. Ее целесообразно использовать при решении задач балансировки нагрузки в телекоммуникационных системах [12].

Таким образом, для обеспечения предсказуемости и стабильности работы сети важно учитывать квазидетерминированные потоки пакетов. Их нужно интегрировать в приложения с высокими требованиями к качеству обслуживания и производительности [13].

Исследователи неоднократно обращались к задаче ограничения воздействия фрактальных характеристик сетевой нагрузки [14]. Известно, например, что можно управлять трафиком на уровне пакетов. Это уменьшает число повторных передач пакетов и структурных сходств между ними [15].

Отдельно стоит указать на необходимость определения оптимальных временны́х интервалов между загрузками пакетов. Это имеет особое значение для управления трафиком и предполагает преобразование самоподобного стохастического потока пакетов в квазидетерминированный.

Описанный в [16] подход обеспечивает преобразование входного потока пакетов с гамма-распределением в квазидетерминированный выходной поток, основанный на решении системы уравнений Линдли. Однако в [16] не приводятся рекомендации по снижению влияния долговременных зависимостей на QoS для других самоподобных распределений.

Целью представленной научной работы является создание метода получения оптимальных вероятностных характеристик выходного потока пакетов. Решение базируется на использовании минимального значения меры близости двух потоков: самоподобного входного и квазидетерминированного выходного.

Материалы и методы. Параметры распределения выходного потока выбрали таким образом, чтобы функция аппроксимации была близка к δ-функции (функция Дирака, она же — функция распределения квазидетерминированного выходного потока). Мера близости входных и выходных распределений временны́х интервалов потоков пакетов — дивергенция (расхождение) Кульбака – Лейблера. Использовались методы теорий множеств, метрических пространств, многомерной оптимизации и телетрафика. В алгоритм решения задачи включили предельный переход к δ-функции, позволяющий восстановить квазидетерминированный поток, а также минимизацию расхождения Кульбака – Лейблера. Для этого нашли частные производные и приравняли их к нулю.

Будем считать, что известны характеристики вероятностного распределения интервалов между пакетами входного трафика f(τ; θ₁, θ₂, …, θ_n). Здесь θ₁, θ₂, …, θ_n — параметры распределения, τ — временное расстояние между пакетами. Показатель Хёрста 0,5 < H < 1, θ₁(H) [17], g(τ; η₁, η₂, …, η_n) — вероятностное распределение значений интервалов между пакетами в выходном потоке без самоподобия с параметрами η₁, η₂, …, η_n.

Условия использования преметрики известны из [17]:

• ρ(f, g) ≥ 0,
• ρ(f, g) ≥ 0 ↔ f ≡ g.

Необходимо определить

1. Вероятностное распределение g(τ;η₁,η₂, …, η_m) на основе его приближения к δ-функции (функции Дирака), обеспечивающей равенство временны́х интервалов квазидетерменированного выходного потока пакетов.
2. Метод, обеспечивающий получение оптимальных вероятностных характеристик выходного потока пакетов.

Решение будет базироваться на минимальном значении меры близости самоподобного входного и квазидетерминированного выходного потоков.

Учтем три ограничения

1. Минимальное значение преметрики ρ(f,g) → min.
2. Функции f(τ;θ₁,θ₂, …, θ_n) и g(τ; η₁, η₂, …, η_m) — кусочно-непрерывные.
3. Функция ρ(f,g) — дифференцируемая по переменным η₁,η₂, …, η_m во всей области определения:
   
   

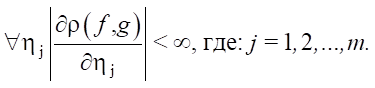
Результаты исследования. Будем считать, что вероятностное распределение квазидетерменированного выходного потока описывается функцией Дирака [18]:

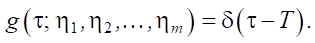
Есть две причины, по которым эту же функцию (или δ-функцию) используем в качестве функции распределения вероятности.

1. Она принимает неотрицательные значения:
   
   

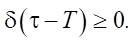
2. Интеграл по всей числовой оси определяется выражением:
   
   

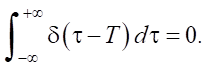
Отметим, что при вычислении значения преметрики ρ(f, g) затруднительно использовать дельта-функцию в качестве функции плотности распределения выходного потока. Кроме того, идеальных детерминированных потоков не бывает в условиях эксплуатации телекоммуникационных сетей. Значит, имеет смысл задействовать вместо детерминированного потока квазидетерминированный. В этом случае при изменении одного параметра функции плотности распределения она будет стремиться в пределе к дельта-функции Дирака.

Рассмотрим равномерное распределение с математическим ожиданием, равным Т, и интервалом значений, равным ΔТ. Функция плотности распределения в этом случае будет иметь вид:

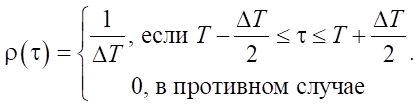
При ΔТ → 0 плотность распределения такого потока ρ(τ) → δ (τ – T).

На практике из-за джиттера невозможно обеспечить равномерные интервалы между пакетами. Чаще всего математические модели телекоммуникационных процессов строятся в предположении, что величина джиттера подчиняется нормальному закону распределения [19]. Для детерминированного потока пакетов временные интервалы между ними распределяются нормально с математическим ожиданием μ = T и стандартным отклонением, которое должно удовлетворять правилу трех сигм [20]: 0 < 3σ ≤ J₀, где J₀ — нормативное значение джиттера.

В [18] установлено, что обусловленный джиттером квазидетерминированный поток с нормальным распределением слабо сходится к δ (τ – T) при δ → 0.

Это значит, что наилучшая аппроксимация детерминированного потока — это квазидетерминированный поток пакетов с нормальным распределением. Его математическое ожидание совпадает с постоянным временны́м интервалом между пакетами μ = T и среднеквадратическим отклонением σ, ограниченным уровнем джиттера J₀:

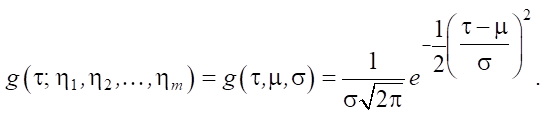
Для достижения цели исследований в качестве преметрики [17] используем дивергенцию Кульбака – Лейблера D_KL(f||g). Учитывая ее свойства и принятые допущения, сформулируем лемму.

Лемма. Пусть f(τ; θ₁, θ₂, …, θ_n) — кусочно-непрерывная функция:

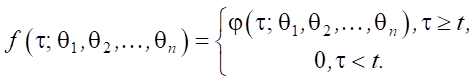(1)

Здесь t ≥ 0 — некоторая пороговая величина, а φ(τ; θ₁, θ₂, …, θ_n) > 0 — непрерывная функция на интервале (t, +∞).

Выходной поток g(τ; μ, σ) подчиняется нормальному распределению интервалов времени между пакетами без самоподобия с параметрами μ и σ > 0.

Требуется доказать, что D_KL(f || g) достигает минимума при равенстве математических ожиданий f и g.

Доказательство. Воспользуемся подходом, изложенным в [17].

Перекрестная энтропия H(f, g) может быть определена двумя способами. Первый:

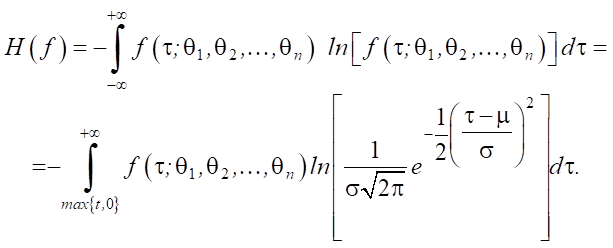(2)

Второй:

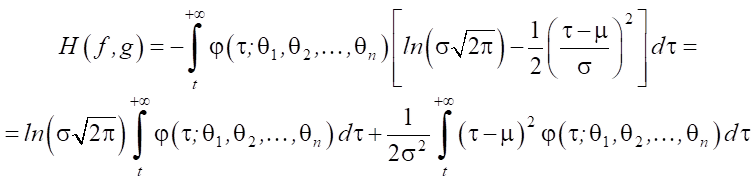(3)

Для функции плотности распределения входного потока пакетов:

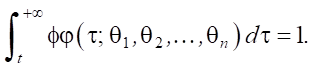
Следовательно:

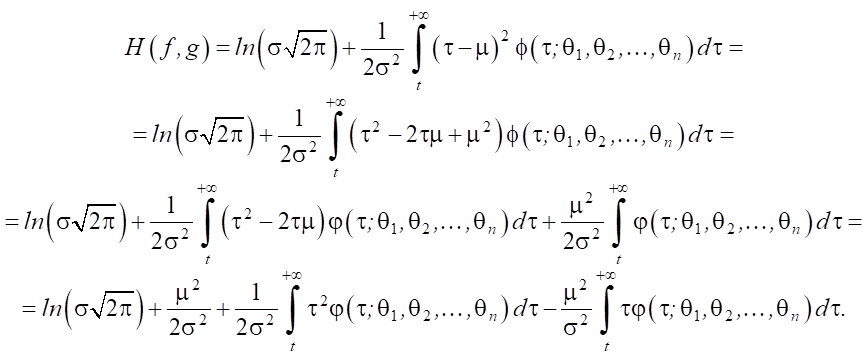(4)

Известно также:

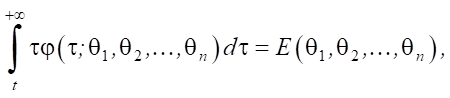
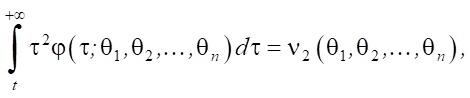
где E — функция, позволяющая определить математическое ожидание входного самоподобного потока пакетов.

Таким образом,

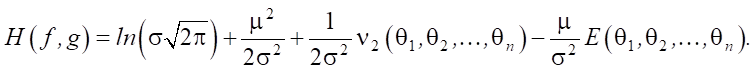(5)

Тогда:

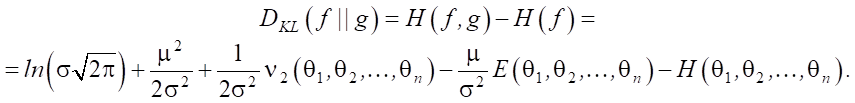(6)

Решим задачу многомерной оптимизации:

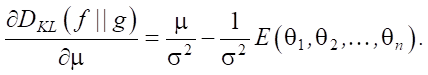(7)

Значит:

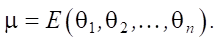
Для нормального распределения

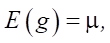
следовательно,

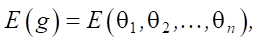
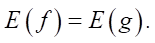
Воспользуемся критерием Сильвестра:

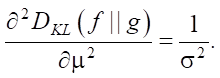(8)

Необходимое и достаточное условие минимума D_KL(f || g) — равенство математических ожиданий входного и выходного потоков пакетов.

Для детерминированного потока временной интервал T между пакетами можно определить по предельному переходу при σ → 0, то есть:

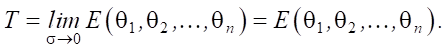(9)

Последнее равенство возможно, поскольку выражение E(θ₁, θ₂, …, θ_n) не содержит в явном виде σ. Следовательно, в рамках данного метода для квазидетерминированного выходного потока временной интервал между пакетами равен математическому ожиданию временных интервалов самоподобного стохастического потока.

Ниже приводится последовательность реализации разработанного метода.

1. В качестве закона распределения интервалов времени между пакетами выходного потока следует использовать нормальный закон со среднеквадратическим отклонением, ограниченным величиной джиттера J₀.
2. Необходимо найти математическое ожидание входного самоподобного потока пакетов E(θ₁,θ₂,…, θ_n) и определить величину математического ожидания μ выходного потока, имеющего нормальное распределение. Для этого используется утверждение ранее доказанной леммы.
3. Для найденного значения μ определяется величина интервала времени μ =T квазидетерминированного выходного потока пакетов.

В качестве примера рассмотрим самоподобный поток с распределением Парето:

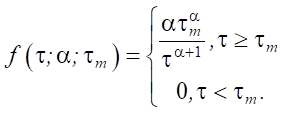(10)

Требуется определить величину μ = ψ(α, τ_m), которая минимизирует D_KL(f || g).

Для распределения Парето:

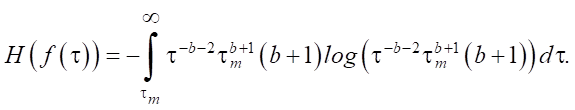(11)

Перекрестная энтропия исследуемых законов равна:

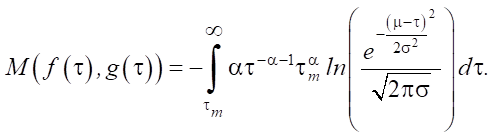(12)

Будем рассуждать так же, как при доказательстве леммы. Получим:

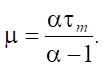(13)

Это выражение соответствует математическому ожиданию распределения Парето.

Найдем вторую производную, и тогда значение μ минимизирует значение D_KL(f || g).

Для получения квазидетерминированного потока выполним предельный переход для найденного значения математического ожидания при σ → 0:

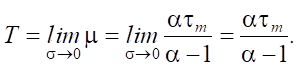(14)

Таким образом, при преобразовании самоподобного входного потока пакетов в квазидетерминированный выходной значение временных интервалов квазидетерминированного потока T совпадает с математическим ожиданием входного потока [21].

Обсуждение и заключение. Проведенное научное исследование открывает новые возможности для обеспечения телекоммуникации в условиях ограниченных сетевых ресурсов. Авторы задействовали математические методы и получили оптимальные вероятностные характеристики выходного потока пакетов, используя минимальное значение меры близости самоподобного входного и квазидетерминированного выходного потоков. Согласно лемме, которая доказана в рамках данной работы, при нормальном распределении для выходного потока минимальное значение дивергенции Кульбака – Лейблера достигается, если равны математические ожидания входного и выходного потоков. Решение задачи многомерной оптимизации доказало адекватность предложенного метода. Следует учитывать его возможности при работе с телекоммуникационными сетями. Использование данного подхода способно ограничить негативное воздействие самоподобия потока и таким образом улучшить качество обслуживания пользователей при сохранении объема информационного обмена.

В перспективе авторы планируют разработать методы снижения самоподобия сетевого трафика. Такой подход, предположительно, будет базироваться на дивергенции Йенсена – Шеннона. Эта мера близости отличается от распределения Кульбака – Лейблера тем, что является полной метрикой и ограничена сверху [22].