Optimization Problem for Probabilistic Time Intervals of Quasi-Deterministic Output and Self-Similar Input Data Packet Flow in Telecommunication Networks

Introduction. Telecommunication networks operate under conditions of increasing loads and traffic growth, which is subject to complex probabilistic distribution laws and cannot be accurately predicted. Self-similarity of the packet flow creates stable dependences, which limits the volume of information exchange between users [1]. In [2], methods were proposed that met the requirements of quality of service (QoS) of the communication. The authors of the mentioned work believed that it was necessary to focus on the priority traffic of new generation networks. However, their solution did not eliminate the problem of self-similarity of packet flows. Millán G. and Lefranc G. proposed a model for managing network flows taking into account the channel capacity, without considering the fractal characteristics of traffic [3]. In [4], techniques for load balancing taking into account the multifractal properties of traffic were developed. However, they did not solve the problem of self-similarity and structural optimization of output flows. Ushanev K.V. and Makarenko S.I. [5], having analyzed methods for increasing the stability of networks taking into account complex traffic characteristics, proposed models for transforming self-similar input flows [6]. In this case, strict mathematical analysis allowed minimizing the differences between the distributions of input and output flows and, consequently, eliminating self-similarity. However, in [6], this solution is absent.

High-quality regular data transmission involves the use of a constant bitrate (CBR) traffic source model [4]. In this model, a node transmits fixed-size packets at equal time intervals T. If the time between sending packets is significantly greater than the transmission time of one packet, then the packet size may be insignificant. As noted in [4], under conditions of the limited bandwidth, this model can be used to maintain traffic stationarity and minimize delays. Paper [7] shows the advantages of CBR for networks with strict requirements for transmission time characteristics, and [8] emphasizes its effectiveness under conditions of high sensor density. According to [9], the predictability of traffic in this model makes it more effective in terms of energy savings, which is critical for energy-constrained devices.

As shown in [10], the CBR model is traditionally associated with wireless sensor networks, but it can also be useful in general purpose networks [11]. It is useful for solving load balancing problems in telecommunication systems [12].

Thus, to ensure predictability and stability of network operation, it is important to consider quasi-deterministic packet flows. They need to be integrated into applications with high quality of service and performance requirements [13].

Researchers have repeatedly addressed the problem of limiting the impact of fractal characteristics of network load [14]. It is known, for example, that it is possible to control traffic at the packet level. This reduces the number of retransmissions of packets and structural similarities between them [15].

The necessity of determining the optimal time intervals between packet downloads is worth mentioning separately. This is of particular importance for traffic management and involves transforming a self-similar stochastic packet flow into a quasi-deterministic one.

The approach described in [16] provides the transformation of the input packet flow with a gamma distribution into a quasi-deterministic output flow based on the solution to the Lindley equation system. However, [16] does not provide recommendations for reducing the impact of long-term dependences on QoS for other self-similar distributions.

The objective of the presented research is to create a method for obtaining optimal probabilistic characteristics of the output packet flow. The solution is based on the use of the minimum value of the measure of closeness of two flows: self-similar input and quasi-deterministic output.

Materials and Methods. Parameters of the output flow distribution were selected so that the approximation function was close to δ-function (the Dirac delta function, also known as the distribution function of the quasi-deterministic output flow). The measure of closeness of the input and output distributions of the time intervals of packet flows is the Kullback–Leibler divergence. Methods of the set theory, metric spaces, multidimensional optimization and teletraffic were used. The algorithm for solving the problem included a passage to the limit of δ-function, which allows restoring the quasi-deterministic flow, as well as minimization of the Kullback-Leibler divergence. To do this, partial derivatives were found and equated to zero.

We assume that the characteristics of the probability distribution of intervals between input traffic packets f(τ; θ₁, θ₂, …, θ_n) are known. Here, θ₁, θ₂, …, θ_n — distribution parameters; τ — time distance between packets. Hurst exponent 0.5 < H < 1, θ₁(H) [17]; g(τ; η₁, η₂, …, η_n) — probability distribution of the values of intervals between packets in the output flow without self-similarity with parameters η₁, η₂, …, η_n.

The conditions for using premetrics are known from [17]:

• ρ(f, g) ≥ 0;
• ρ(f, g) ≥ 0 ↔ f ≡ g.

It is necessary to determine:

1. probability distribution g(τ; η₁, η₂, …, η_m) based on its approximation to δ-function (Dirac function), providing the equality of time intervals of the quasi-deterministic output packet flow;
2. method that provides obtaining optimal probabilistic characteristics of the output packet flow.

The decision is based on the minimum value of the measure of closeness of the self-similar input and quasi-deterministic output flows.

We take into account three restrictions:

1. minimal value of premetrics ρ(f, g) → min;
2. functions f(τ; θ₁, θ₂, …, θ_n) and g(τ; η₁, η₂, …, η_m) — piecewise continuous;
3. function ρ(f, g) — differentiable with respect to variables η₁, η₂, …, η_m in the entire domain of definition:
   
   

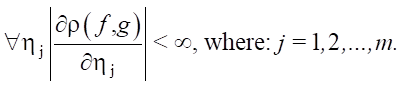
Research Results. We assume that the probability distribution of the quasi-deterministic output flow is described by the Dirac function [18]:

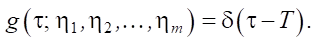
There are two reasons why we use this same function (or δ-function) as the probability distribution function.

1. It takes non-negative values:
   
   

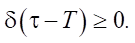
2. The integral over the entire number axis is determined by the expression:
   
   

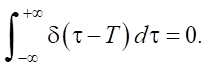
Note that when calculating the premetric value ρ(f, g), it is difficult to use the delta function as the output flow distribution density function. In addition, ideal deterministic flows do not exist under the operating conditions of telecommunication networks. Therefore, it makes sense to use a quasi-deterministic flow instead of a deterministic one. In this case, when changing one parameter of the distribution density function, it tends to the Dirac delta function in the limit.

Let us consider a uniform distribution with a mathematical expectation equal to Т, and a range of values equal to ΔТ. The distribution density function in this case will have the form:

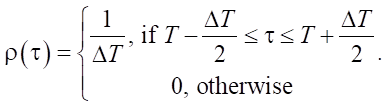
At ΔТ → 0, the distribution density of this flow ρ(τ) → δ (τ – T).

In practice, jitter makes it impossible to maintain uniform intervals between packets. Most often, mathematical models of telecommunication processes are built on the assumption that the jitter value obeys the normal distribution law [19]. For a deterministic packet flow, the time intervals between them are distributed normally with mathematical expectation μ = T and standard deviation that must satisfy the three-sigma rule [20]: 0 < 3σ ≤ J₀, where J₀ — normative value of jitter.

In [18], it is established that a jitter-induced quasi-deterministic flow with a normal distribution converges weakly to δ (τ – T) at δ → 0.

This means that the best approximation to a deterministic flow is a quasi-deterministic packet flow with a normal distribution. Its mathematical expectation coincides with a constant time interval between packets μ = T and standard deviation σ, limited by jitter level J₀:

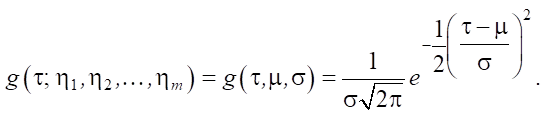
To achieve the research objective, we use the Kullback-Leibler divergence as premetrics [17] D_KL(f||g). Taking into account its properties and the adopted assumptions, we formulate the lemma.

Lemma. Let f(τ; θ₁, θ₂, …, θ_n) be piecewise continuous function:

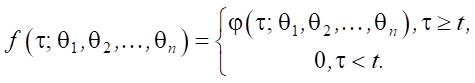(1)

Here, t ≥ 0 — some threshold value, and φ(τ; θ₁, θ₂, …, θ_n) > 0 — continuous function on interval (t, +∞).

Output flow g(τ; μ, σ) obeys the normal distribution of time intervals between packets without self-similarity with parameters μ and σ > 0.

It is required to prove that D_KL(f || g) reaches a minimum when the mathematical expectations f and g are equal.

Proof. We use the approach described in [17].

Cross entropy H(f, g) can be defined in two ways.

The first:

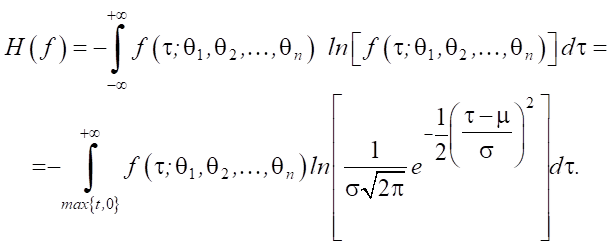(2)

The second:

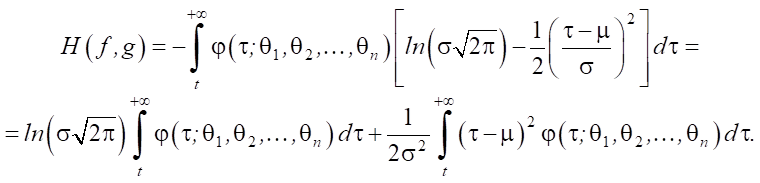(3)

For the density function of the input packet flow:

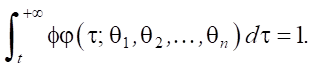
Hence:

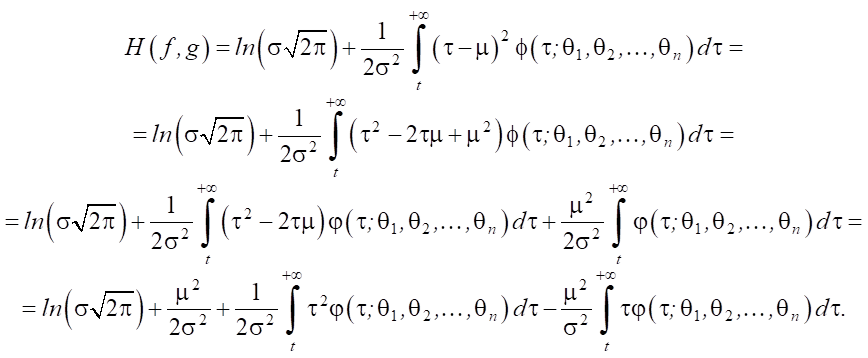(4)

It is also known:

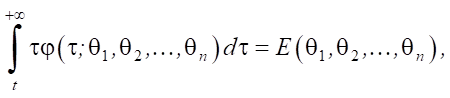
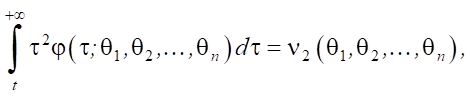
where E — function that provides determining the mathematical expectation of an input self-similar packet stream.

Thus,

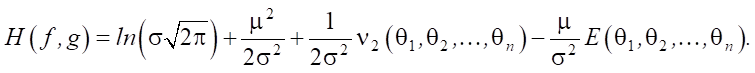(5)

Then:

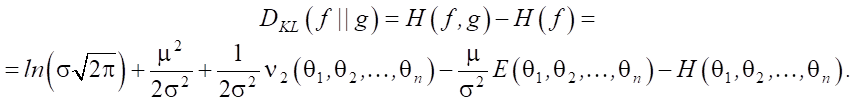(6)

Let us solve the problem of multidimensional optimization:

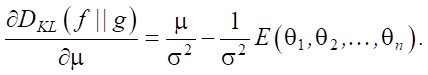(7)

It means:

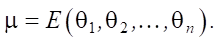
For normal distribution:

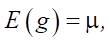
consequently,

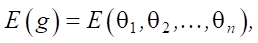
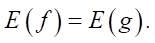
Let us use Sylvester's criterion:

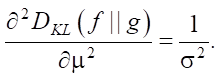(8)

A necessary and sufficient condition for the minimum D_KL(f || g) is the equality of the mathematical expectations of the input and output packet flows.

For a deterministic flow, time interval T between packets can be determined by the limit transition as σ → 0, that is:

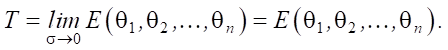(9)

The last equality is possible because expression E(θ₁, θ₂, …, θ_n) does not explicitly contain σ. Therefore, within the framework of this method, for a quasi-deterministic output flow, the time interval between packets is equal to the mathematical expectation of the time intervals of a self-similar stochastic flow.

The sequence of implementation of the developed method is given below.

1. The normal law with the standard deviation limited by jitter value J₀ should be used as the law of distribution of time intervals between packets of the output flow.
2. It is necessary to find the mathematical expectation of the input self-similar packet flow E(θ₁, θ₂, …, θ_n) and determine the value of mathematical expectation μ of the output flow, which has a normal distribution. For this, the statement of the previously proven lemma is used.
3. For the found value μ, time interval μ = T of the quasi-deterministic output packet flow is determined.

As an example, consider a self-similar flow with the Pareto distribution:

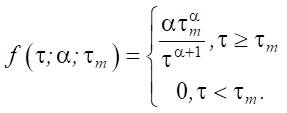(10)

It is required to determine value μ = ψ(α, τ_m) that minimizes D_KL(f || g).

For the Pareto distribution:

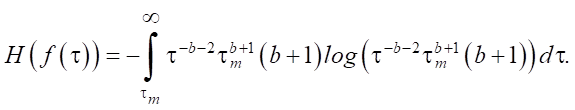(11)

The cross entropy of the laws under study is equal to:

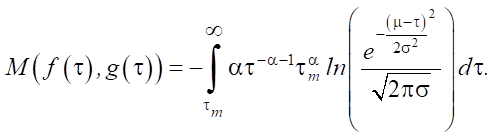(12)

We reason in the same way as when proving the lemma. We obtain:

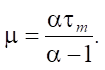(13)

This expression corresponds to the mathematical expectation of the Pareto distribution.

Let us find the second derivative, and then value μ minimizes value D_KL(f || g).

To obtain a quasi-deterministic flow, we perform the limit transition for the found value of the mathematical expectation at σ → 0:

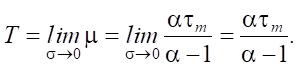(14)

Thus, when transforming a self-similar input packet stream into a quasi-deterministic output stream, the value of the time intervals of the quasi-deterministic flow T coincides with the mathematical expectation of the input flow [21].

Discussion and Conclusion. The conducted research opens up new possibilities for providing telecommunications under conditions of limited network resources. The authors used mathematical methods and obtained optimal probabilistic characteristics of the output packet flow using the minimum value of the measure of closeness of the self-similar input and quasi-deterministic output flows. According to the lemma proved in this paper, for a normal distribution for the output flow, the minimum value of the Kullback-Leibler divergence is achieved if the mathematical expectations of the input and output flows are equal. The solution to the multidimensional optimization problem verified the adequacy of the proposed method. Its capabilities should be taken into account when working with telecommunication networks. The use of this approach can limit the negative impact of flow self-similarity and thus improve the quality of user service while maintaining the volume of information exchange.

In the future, the authors plan to develop methods for reducing the self-similarity of network traffic. Such an approach will presumably be based on the Jensen-Shannon divergence. This measure of closeness differs from the Kullback-Leibler distribution in that it is a complete metric and is bounded from above [22].