Перейти к:
Прогнозирование сроков доставки товаров в цепях поставок с использованием методов машинного обучения
https://doi.org/10.23947/2687-1653-2025-25-2-120-128
EDN: QBDMMA
Аннотация
Введение. Развитие торговли требует внедрения технологий искусственного интеллекта и машинного обучения для повышения точности прогнозов доставки. Опубликованные на сегодня научные изыскания в этой области представляются недостаточными по двум причинам. Первая: рассматриваются главным образом глобальные цепи поставок, хотя вопрос актуален и для локальных бизнесов. Вторая: прогнозирование, как правило, требует больших объемов данных для машинного обучения и значительных вычислительных ресурсов, недоступных основной массе компаний. Представленное исследование призвано восполнить эти пробелы и показать эффективность использования открытых, доступных данных и известных алгоритмов. Цель работы — описать схему обоснованного выбора наименее ресурсоемкой модели прогнозирования доставки на основе анализа алгоритмов машинного обучения.
Материалы и методы. Использовался набор открытых данных DataCo Smart supply chain for big data analysis о поставках в онлайн-торговле. Для обработки и анализа информации задействовали методы очистки данных, устранения мультиколлинеарности, нормализации и кодирования категориальных признаков. С очищенными данными работали алгоритмы: Decision tree, Random forest, K-nearest neighbors, Naive Bayes, Linear discriminant analysis, XGBoost, CatBoost, LightGBM, AdaBoost и Perceptron.
Результаты исследования. Базовым алгоритмом для модели прогнозирования доставки стал алгоритм дерева решений (Decision Tree). Этот выбор обусловлен высокой точностью, простотой использования и низким риском переобучения. Оценка модели показала высокий и близкий к единице коэффициент детерминации (0,986). При этом фиксируются низкие значения среднеквадратичной ошибки (0,0367) и средней абсолютной ошибки (0,0324). Модель показала удовлетворительные результаты по времени, затраченному на обучение (3,3087 с) и на прогнозирование (0,0051 с). Фактические и предсказанные значения почти идеально совпали. Отклонения от фактических значений оказались минимальными.
Обсуждение и заключение. Предложенная модель эффективна и обладает высокой предсказательной способностью. Качественное прогнозирование сроков доставки товара возможно без привлечения обширных баз данных и мощных вычислительных ресурсов. Исследование открывает перспективу качественной организации логистических операций для средних и малых предприятий. В дальнейших изысканиях целесообразно интегрировать в модель данные о погоде, дорожной ситуации и другие показатели. Использование такой информации в режиме реального времени повысит адаптивность и точность прогнозирования.
Ключевые слова
Для цитирования:
Резванов В.К., Ромакина О.М., Зайцева Е.В. Прогнозирование сроков доставки товаров в цепях поставок с использованием методов машинного обучения. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):120-128. https://doi.org/10.23947/2687-1653-2025-25-2-120-128. EDN: QBDMMA
For citation:
Rezvanov V.K., Romakina O.M., Zaytseva E.V. Forecasting Delivery Time of Goods in Supply Chains Using Machine Learning Methods. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):120-128. https://doi.org/10.23947/2687-1653-2025-25-2-120-128. EDN: QBDMMA
Введение. В условиях развития торговли повышается актуальность точного прогнозирования сроков доставки. Недостаточная эффективность традиционных методов планирования обусловлена неопределенностью, связанной с влиянием различных факторов. Очевидно, что применение в логистике искусственного интеллекта (ИИ) может
значительно улучшить точность прогнозов и сократить операционные затраты. По данным международной консалтинговой организации McKinsey & Company, предприятия, использующие ИИ для управления цепочками поставок, могут сократить ошибки прогнозов на 20–50 %, что в конечном итоге снижает издержки на 10–15 %1.
Опубликованные научные работы, посвященные этой теме, рассматривают главным образом масштабные, глобальные цепи поставок [1]. Активно обсуждаются различные подходы к прогнозированию сроков доставки, однако исследования концентрируются, как правило, на сложных и ресурсоемких моделях, недоступных основной части предприятий — малых и средних. При этом проблема, безусловно, актуальна и для локальных, небольших бизнесов, остро нуждающихся в сбережении ресурсов. Этому способствуют в целом лучшие настройки логистических процессов и, в частности, точное прогнозирование сроков доставки. У компаний с ограниченными информационными и вычислительными возможностями мало инструментов для улучшения ситуации. Представленное исследование призвано восполнить этот пробел. Цель работы — определение наиболее эффективной и наименее ресурсоемкой модели машинного обучения для прогнозирования сроков доставки.
Материалы и методы. В исследовании использовался набор структурированных данных о продажах, доставках, клиентах и финансовых показателях. Открытый набор данных DataCoSupplyChainDataset размещен компанией DataCo Global в бесплатном коллективном облачном репозитории Mendeley Data. Основные сведения этого набора: даты заказа и доставки, информация о клиентах, финансовые показатели заказов и статус доставки.
До анализа и моделирования данные прошли предварительную обработку — очистку и преобразование. Для достижения поставленной цели в первую очередь выявили корреляции и устранили мультиколлинеарность на основе матрицы корреляции (рис. 1).
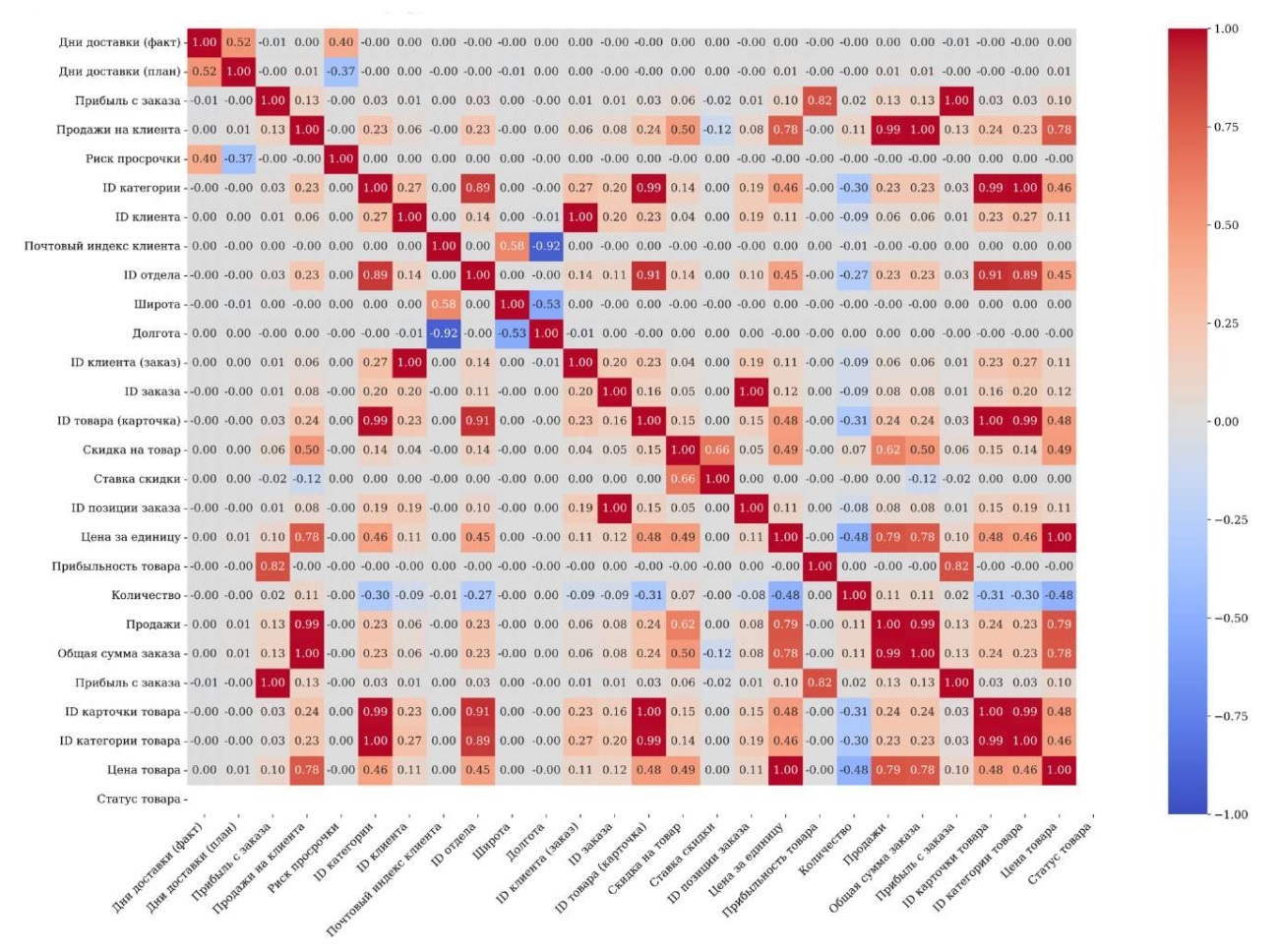
Рис. 1. Матрица корреляции
Матрица позволила выявить несколько пар признаков с коэффициентом корреляции, равным 1. Это указывает на их полное дублирование. Ниже представлены эти пары признаков.
- Customer_id (идентификатор клиента) и order_customer_id (идентификатор клиента для заказа).
- Sales_per_customer (продажи на клиента) и order_item_total (сумма за заказанный товар).
- Benefit_per_order (прибыль с заказа) и order_profit_per_order (прибыль на заказ).
- Order_item_cardprod_id (идентификатор карточки товара в заказе) и product_card_id (идентификатор карточки товара).
- Category_id (идентификатор категории) и product_category_id (идентификатор категории продукта).
- Order_item_product_price (цена товара в заказе) и product_price (цена продукта).
Для устранения дублирования удалены следующие признаки:
- benefit_per_order (прибыль с заказа);
- sales_per_customer (продажи на клиента);
- order_item_cardprod_id (идентификатор карточки товара в заказе);
- order_item_product_price (цена товара в заказе);
- product_category_id (идентификатор категории продукта);
- order_customer_id (идентификатор клиента для заказа).
Также было обнаружено, что признак product_status (доступность товара) имеет только одно уникальное значение (0), то есть товар всегда доступен. Этот признак также удалили.
Для анализа мультиколлинеарности между числовыми признаками использовали коэффициент инфляции дисперсии (англ. variance inflation factor, VIF) [2]. Признаки с VIF выше 5 указывают на сильную взаимосвязь с другими признаками, что может исказить результаты анализа и моделей. Во избежание этой проблемы такие признаки удаляются или объединяются. Таким образом сокращается избыточность данных и повышается стабильность модели.
После предварительной обработки выбрали основные числовые и категориальные признаки для дальнейшего анализа и построения модели.
Числовые признаки включают такие показатели, как продажи, прибыль, скидки и количество товаров в заказе. Категориальные признаки включают статус доставки, сегмент клиентов и режим доставки.
По признакам с VIF выше 5 провели дальнейший анализ для выявления избыточных взаимосвязей. Если признак мог быть выражен через другие, его заменяли комбинацией более простых признаков. Примеры представлены ниже.
- Sales = product_price * Поскольку выручка с продажи (sales) напрямую зависит от цены продукта (product_price) и количества товара (order_item_quantity), решено использовать это выражение для замены избыточных признаков.
- Order_item_discount = sales * Скидка на товар (order_item_discount) напрямую зависит от объема выручки с продажи и ставки скидки (order_item_discount_rate), что делает этот признак также избыточным.
- Order_item_total = sales – order_item_discoun. Здесь общая сумма заказа (order_item_total) выражена через выручку с продажи и скидку на товар, что позволило уменьшить дублирование данных.
- Order_profit_per_order = order_item_total * Прибыль на заказ (order_profit_per_order) связана с общей стоимостью товара и коэффициентом прибыли на товар (order_item_profit_ratio), что делает возможным ее вычисление через другие признаки.
Отсутствующие значения в столбце order_zipcode (почтовый индекс заказа) заменили на customer_zipcode (почтовый индекс клиента).
Данные в столбце days_for_shipping_real (дней для доставки, фактически) привели к нормальной форме вещественного числа с плавающей запятой.
В исходном наборе данных признаки «статус доставки», «сегмент клиентов» и «режим доставки» были категориальными, что существенно затрудняло использование числовых моделей машинного обучения. С помощью метода Label Encoder2 эти признаки были преобразованы в числовой формат:
- категориям «отправлено», «в пути» и «доставлено» признака delivery_status были сопоставлены значения 0, 1 и 2 соответственно;
- категориям признака customer_segment также были сопоставлены уникальные числовые значения.
Описанный подход позволяет сохранить различия между категориями и при этом использовать категории в процессе машинного обучения.
При выборе оптимальной модели машинного обучения для прогнозирования сроков доставки реализовали ряд алгоритмов машинного обучения. Decision tree [3] — один из наиболее распространенных алгоритмов машинного обучения, применяющийся для задач, связанных с принятием решений на основе набора признаков. По значениям некоторых признаков алгоритм разбивает данные на меньшие подгруппы и затем структурирует в виде дерева решений.
Алгоритм работает следующим образом.
- Перед первым шагом в корневом узле дерева решений содержится исходный набор данных.
- На каждом шаге алгоритма выбирается признак, позволяющий наиболее эффективно разделить данные на подмножества и одно или несколько его пороговых значений. Данные разделяются на группы в соответствии с выбранными значениями признака. Процесс повторяется до тех пор, пока не будут достигнуты листовые узлы, содержащие итоговые решения и не подлежащие дальнейшей декомпозиции.
Таким образом, каждый узел дерева — это точка принятия решения, в которой происходит разделение данных на основе значения некоторого признака. Ветви дерева соответствуют возможным результатам такого разделения.
Ключевой момент работы алгоритма — определение признака разбиения данных на каждом шаге.
Предварительные эксперименты показали, что критерий Джини обеспечивает наилучшую точность разбиения данных в рамках поставленной задачи, поэтому именно он использовался в представленной работе.
Для определения оптимального алгоритма на подготовленном наборе данных протестировали Random Forest [4], K-Nearest Neighbors [5], Naive Bayes [6], Linear Discriminant Analysis [7], XGBoost [8], CatBoost [9], LightGBM [10], AdaBoost [11] и Perceptron [12]. Эти алгоритмы выбрали благодаря их распространенности и подтвержденной эффективности для решения задач прогнозирования. Каждую модель тестировали на одном и том же наборе данных после одинаковой процедуры предварительной обработки. Для оценки эффективности моделей использовались метрики R² (коэффициент детерминации), средняя квадратичная ошибка (англ. mean square error, MSE), средняя абсолютная ошибка (англ. mean absolute error, MAE), а также время, затраченное на обучение и прогнозирование. Перечисленные метрики позволяют объективно сравнить точность и ресурсоемкость алгоритмов и выбрать оптимальную модель для прогнозирования сроков доставки.
Результаты исследования. На рис. 2 показана оценка качества описанных выше моделей с помощью перечисленных метрик. Decision Tree и Random Forest продемонстрировали наиболее высокую точность. Однако следует учитывать простоту и интерпретируемость Decision Tree, а также его меньшую склонность к переобучению [13] по сравнению с более сложными моделями. В связи с этим для прогнозирования сроков доставки товаров использовался алгоритм Decision Tree.
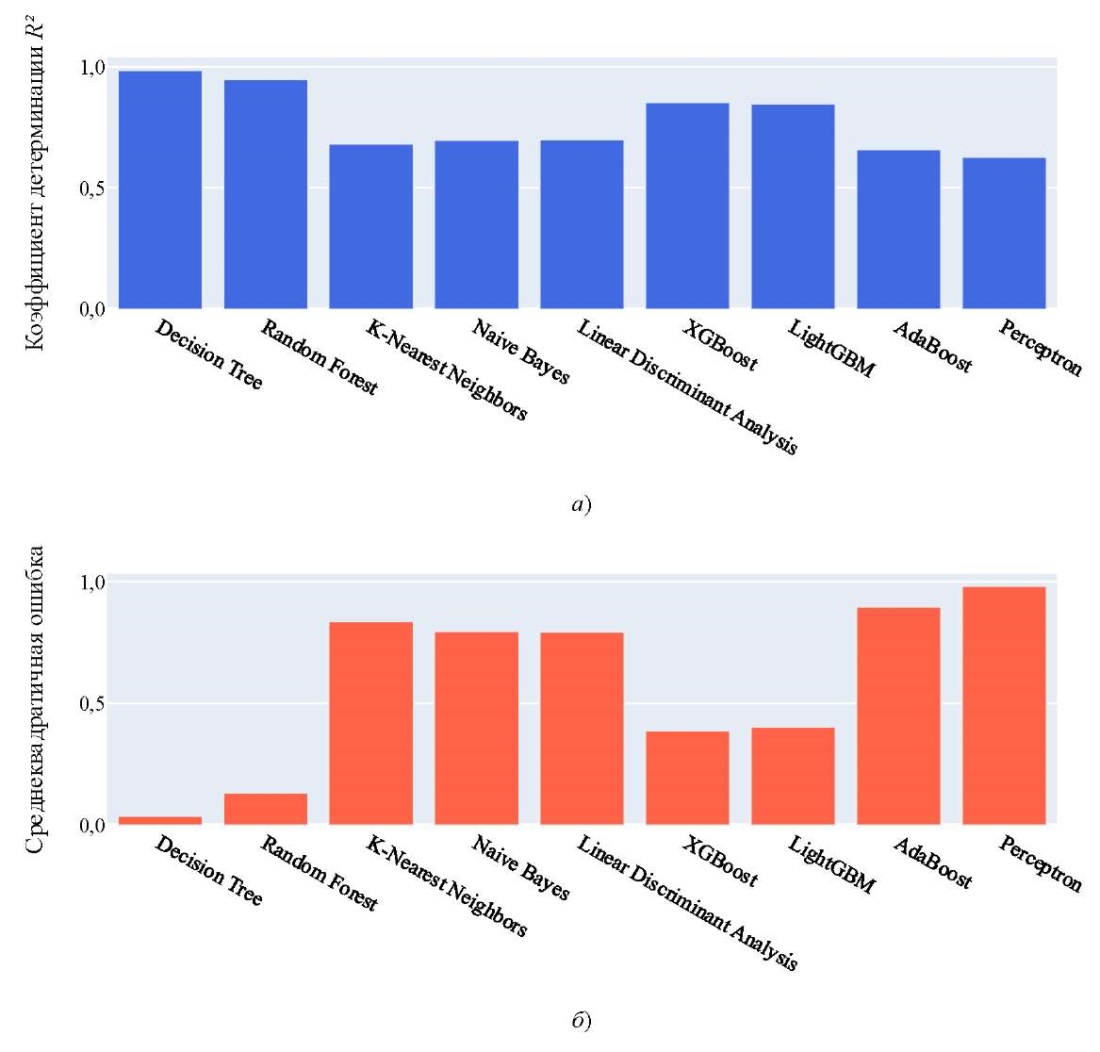

Рис. 2. Оценка качества моделей:
а — оценка качества моделей с помощью метрики R²;
б — оценка качества моделей с помощью метрики MSE;
в — оценка качества моделей с помощью метрики MAE;
г — время, затраченное моделями на обучение, с;
д — время, затраченное моделями на предсказание, с
Итак, тестирование модели Decision tree дало следующие результаты:
- коэффициент детерминации — 0,986;
- среднеквадратичная ошибка (MSE) — 0,0367;
- средняя абсолютная ошибка (MAE) — 0,0324;
- время на обучение — 3,3087 с;
- время на предсказание — 0,0051 с.
Высокое значение R² и низкие значения MSE и MAE указывают на высокую точность и эффективность модели.
Рассмотрим соответствие фактических значений и значений, предсказанных моделью (рис. 3).
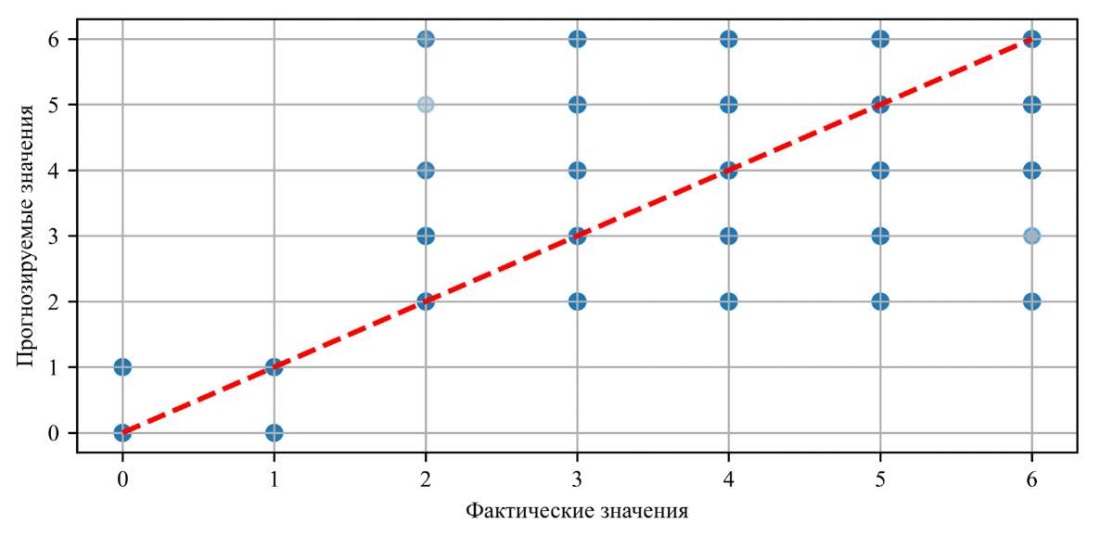
Рис. 3. График фактических и предсказанных значений
Как видим, синие точки (предсказанные значения) расположены близко к красной штриховой линии, которая представляет собой линию идеального совпадения между фактическими и предсказанными значениями. Это указывает на высокую точность предсказания значений.
Плотное расположение точек вдоль штриховой линии говорит об отсутствии значительных смещений в сторону завышения или занижения показателей. Это указывает на баланс между предсказанными и фактическими значениями.
Группировка точек вдоль диагонали показывает, что отклонения от фактических значений минимальны. Таким образом, можно обоснованно говорить о крайне незначительных ошибках и высокой предсказательной способности модели.
Обсуждение и заключение. Результаты экспериментов показали, что модель на основе дерева решений способна с высокой точностью предсказывать сроки доставки товаров. Это подтверждается высокими значениями R² и низкими значениями MSE и MAE. Установлено также, что модель достаточно быстро обучается и выполняет прогноз, то есть хорошо подходит для использования в реальных условиях. В этом смысле особенно ценно то, что операции реализуются при минимальных затратах вычислительных ресурсов.
Отметим основные условия достижения хороших результатов:
- качественная предварительная обработка данных;
- устранение мультиколлинеарности;
- применение оптимального критерия разбиения данных.
Научную значимость представленной работы следует рассматривать как с теоретической, так и с прикладной точки зрения. В первом случае речь идет о возможности успешного применения простых и эффективных моделей машинного обучения в логистике. Показано, что эти модели могут обеспечить необходимую точность прогнозов, существенно снизить операционные расходы и оптимизировать ресурсы предприятий. Авторы представленной статьи выбирали из девяти алгоритмов, каждый из которых может оказаться оптимальным для решения той или иной логистической (или, шире, — экономической) проблемы предприятия. Перечислим лишь некоторые логистические задачи, которые можно попытаться решить с помощью подхода, описанного в данной статье:
- выбор схемы доставки с учетом требований к свежести товара;
- выбор схемы доставки с учетом затрат на горюче-смазочные материалы;
- оптимизация закупок с учетом расходов по складированию;
- формирование зарплатной политики в логистическом подразделении;
- прогнозирование ликвидности товаров.
Это подводит ко второму — прикладному — потенциалу описанных в статье научных изысканий. Ожидаемый итоговый практический эффект — лучшая управляемость и рентабельность логистики. Это особенно важно для малого и среднего бизнеса. Крупные корпорации для выстраивания эффективной логистики содержат собственные штаты аналитиков и программистов, формируют собственные базы данных или закупают эксклюзивную информацию. Небольшие компании могут для этих же целей воспользоваться накопленными ими в ходе работы наборами данных и известными алгоритмами. Отметим, однако, что предложенный подход также можно задействовать в качестве базовой модели для более сложных систем управления цепями поставок.
Дальнейшие исследования могут быть направлены на интеграцию дополнительных источников данных, таких как текущая дорожная ситуация, погодные условия и макроэкономические показатели. Использование такой информации в режиме реального времени может обеспечить увеличение точности прогнозирования и адаптивности моделей.
1. DocShipper Group. How AI is Changing Logistics & Supply Chain in 2025? URL: https://docshipper.com/logistics/ai-changing-logistics-supply-chain-2025/
(дата обращения: 22.03.2025).
2. Метод преобразует данные, представляющие категориальные значения, в целые числа 0, 1, 2 и т.д., соответствующие каждой категории.
Список литературы
1. Корчагина Е.В., Корчагина Д.А., Ромакина О.М., Арсеньева А.З. Применение технологий искусственного интеллекта в логистике и управлении глобальными цепями поставок: анализ зарубежных научных публикаций. Риск: ресурсы, информация, снабжение, конкуренция. 2024;(1):29–33. https://doi.org/10.56584/1560-8816-2024-1-29-33
2. Midi H, Bagheri A. Robust Estimations as a Remedy for Multicollinearity Caused by Multiple High Leverage Points. Journal of Mathematics and Statistics. 2009;5(4):311–318. https://doi.org/10.3844/JMSSP.2009.311.321
3. Patel HН, Prajapati P. Study and Analysis of Decision Tree Based Classification Algorithms. International Journal of Computer Sciences and Engineering. 2018;6(10):74–78. https://doi.org/10.26438/ijcse/v6i10.7478
4. Louppe G. Understanding Random Forests: From Theory to Practice. PhD diss. Liège: University of Liège; 2014. 213 p. https://doi.org/doi:10.13140/2.1.1570.5928
5. Zhongheng Zhang. Introduction to Machine Learning: k-Nearest Neighbors. Annals of Translational Medicine. 2016;4(11):218–218. https://doi.org/10.21037/atm.2016.03.37
6. Taheri S, Mammadov M. Learning the Naive Bayes Classifier with Optimization Models. International Journal of Applied Mathematics and Computer Science. 2013;23(4):727–739. https://doi.org/10.2478/amcs-2013-0059
7. Jianhang Zhou, Qi Zhang, Shaoning Zeng, Bob Zhang, Leyuan Fang. Latent Linear Discriminant Analysis for Feature Extraction via Isometric Structural Learning. Pattern Recognition. 2023;149:110218. https://doi.org/10.1016/j.patcog.2023.110218
8. Tianqi Chen, Carlos Guestrin. XGBoost: A Scalable Tree Boosting System. In: Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM; 2016. P. 785–794. https://doi.org/10.1145/2939672.2939785
9. Prokhorenkova L, Gusev G, Vorobev A, Dorogush A, Gulin A. CatBoost: Unbiased Boosting with Categorical Features. Advances in Neural Information Processing Systems. 2018;31:6638–6648. https://doi.org/10.48550/arXiv.1706.09516
10. Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, et al. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In: Proc. 31st International Conference on Neural Information Processing Systems (NeurIPS). Long Beach, CA: Curran Associates Inc.; 2017. P. 3149–3157. URL: https://www.researchgate.net/publication/378480234_LightGBM_A_Highly_Efficient_Gradient_Boosting_Decision_Tree (accessed: 22.02.2025).
11. Jianghua Duan, Hongfei Ye, Hongyu Zhao, Zhiqiang Li. Deep Cascade AdaBoost with Unsupervised Clustering in Autonomous Vehicles. Electronics. 2023;12(1):44. https://doi.org/10.3390/electronics12010044
12. Ke-Lin Du, Chi-Sing Leung, Wai Ho Mow, MNS Swamy. Perceptron: Learning, Generalization, Model Selection, Fault Tolerance, and Role in the Deep Learning Era. Mathematics. 2022;10(24):4730. https://doi.org/10.3390/math10244730
13. Zadvornaya IA, Romakina OM. Application of the Algorithm “Decision Trees” to Analysis of Personal Information of Potential Bank Clients. Cloud of Science. 2019;6(3):415–424.129
Об авторах
В. К. РезвановРоссия
Владислав Константинович Резванов, магистрант, факультет «Прикладная информатика»
197101, г. Санкт-Петербург, Кронверкский пр., 49 а
О. М. Ромакина
Россия
Оксана Михайловна Ромакина, кандидат физико-математических наук, доцент, факультет «Прикладная информатика»
197101, г. Санкт-Петербург, Кронверкский пр., 49 а
Е. В. Зайцева
Россия
Екатерина Викторовна Зайцева, кандидат технических наук, доцент, кафедра «Информатика и компьютерные технологии»
199106, Санкт-Петербург, 21-я линия Васильевского острова, 2
Представлено исследование применения алгоритмов машинного обучения для прогнозирования сроков доставки в логистике. Метод деревьев решений обеспечил высокую точность предсказаний с коэффициентом детерминации 0,986 и оказался наименее ресурсоемким. Применение предложенного алгоритма позволит малым и средним предприятиям оптимизировать свои логистические операции при минимальных затратах вычислительных ресурсов. Полученные результаты открывают новые возможности для улучшения управления цепями поставок с использованием простых моделей машинного обучения.
Рецензия
Для цитирования:
Резванов В.К., Ромакина О.М., Зайцева Е.В. Прогнозирование сроков доставки товаров в цепях поставок с использованием методов машинного обучения. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):120-128. https://doi.org/10.23947/2687-1653-2025-25-2-120-128. EDN: QBDMMA
For citation:
Rezvanov V.K., Romakina O.M., Zaytseva E.V. Forecasting Delivery Time of Goods in Supply Chains Using Machine Learning Methods. Advanced Engineering Research (Rostov-on-Don). 2025;25(2):120-128. https://doi.org/10.23947/2687-1653-2025-25-2-120-128. EDN: QBDMMA
JATS XML














































