Scroll to:
Mathematical Modeling of Charge Power Assessment with Exclusion of Loess Subsidence by Deep Hydraulic Blasts
https://doi.org/10.23947/2687-1653-2025-25-3-233-241
EDN: OVUJUV
Abstract
Introduction. Subsidence loess soils, widespread in Russia, China and Central Asia, are a challenge in modern construction due to their tendency to subsidence and low strength under external loads. Insufficient attention to their mechanical-and-physical properties can cause deformation of structures, which creates a safety hazard and financial losses. Scientific research in this area is fragmentary and does not provide sufficient understanding of compaction methods and their impact on the durability of structures. Moreover, there are no developed optimized mathematical models to predict the efficiency of engineering and technology processes of compaction. Thus, the objective of this study is to develop a mathematical model that determines the explosive charge capacity for compaction of loess. This model is aimed at eliminating the experimental stage, which improves the quality of compaction and contributes to saving financial resources in construction.
Materials and Methods. Mathematical modeling was carried out by including the solution to the inverse applied problem of assessing the power of an explosive charge when eliminating loess subsidence. Initial-boundary value problems with a semiempirical partial differential equation describing the compaction of loess with and without the ejection of soil onto the construction site’s surface were considered by analyzing specific models and mathematical approaches. Based on the solution to these problems using the analytical method, a mathematical model for assessing the power of an explosive charge was developed. The power was determined numerically using two methods: calculations in a program developed in the Python language, and modeling a computational experiment with an assessment of the error of the result. In this case, the effect of the mechanical-and-physical properties of soils, their isotropy and anisotropy were taken into account.
Results. A mathematical model of the explosive charge power during compaction of subsiding loess using deep hydraulic blasts was constructed. The density of dry soil before and after compaction, the vertical diffusion coefficient, dispersion coordinate changes of gas in the compacted soil, and the depth of the explosive charge were taken into account. With an average density of dry compacted soil, the absolute error of the calculated values of the charge power was 3.28 g for compaction of loess without ejection, and 21.13 g for the situation with soil ejection onto the surface. The adequacy of the proposed mathematical solution to the experimental data of a full-scale construction site was shown.
Discussion. The proposed model allows for the assessment of the explosive charge power for isotropic and anisotropic geological systems. The resulting analytical representations demonstrate the degree and nature of the influence of mechanical-and-physical properties of soils on the magnitude of the charge power. Numerical comparison with both experimental data on natural soil compaction and recommendations for compaction of subsidence soils of high power by the hydraulic blasting method has shown that the proposed mathematical model is consistent with empirical data.
Conclusion. The main result of the study is a mathematical model of the explosive charge power when eliminating loess subsidence using deep hydraulic blasts. Analytical representations of the charge power are constructed taking into account the mechanical-and-physical properties of soils. A numerical estimate of the power consistent with the values of empirical data is obtained. The practical significance of the study involves the possibility of using the mathematical model as a calculation method and implementing it in research and design organizations. Further study will be aimed at constructing solutions using mathematical modeling and other inverse problems within the framework of the engineering and technology process of soil compaction.
Keywords
For citations:
Tarasenko E.O. Mathematical Modeling of Charge Power Assessment with Exclusion of Loess Subsidence by Deep Hydraulic Blasts. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):233-241. https://doi.org/10.23947/2687-1653-2025-25-3-233-241. EDN: OVUJUV
Introduction. Research into the surface of the earth's crust has shown the distribution of structurally unstable subsidence loess soils throughout the world. They predominate in Russia [1], China [2] and Central Asia [3]. Loess covers about 17% of Russia's territory. Loess soils are most often found in the North Caucasus, southern Russia, Crimea and other areas.
On a planetary scale, loess is a rock of the Quaternary period. It is characterized by yellow, yellow-brown or yellow-fawn colors [4]. Loess has low density and high macroporosity, which allows water to penetrate deeply into the soil structure. This causes rapid soaking [5] and subsidence [6]. Calculated subsidence from its own weight reaches values of 2.5 m [7].
It is not possible to construct safe and durable buildings and structures on subsidence soils. Designing and constructing objects on loess, as well as insufficient research of their physical and mechanical properties, lead to deformations of buildings and structures, reducing their safe service life. As a result, financial costs grow, and the security threat rapidly increases.
The elimination of subsidence is carried out by various methods, whose selection depends on the conditions of their implementation. This paper examines the method of compaction of loess by deep hydraulic blasts, showing economic efficiency at low production costs [8].
The engineering and technology process of compaction is performed on the basis of a comprehensive detailed study of the mechanical-and-physical properties of subsidence loess soils, which are widely presented in modern literature. Studies have been conducted on the permeability of subsidence soils [9], the deformation characteristics of loess [10] with different moisture content, compaction energy [11], creep [12] and mechanical stability of clays [13]. Strength and deformation properties of clayey soils from the point of view of physical-chemical theory are analyzed under the action of external loads, compressive load, counterpressure [14]. However, a mathematical description of the mechanical-and-physical properties of subsidence clays and loams, as well as their changes as a result of compaction by deep blasts, is not carried out in the noted works. Research is performed on the basis of field and compression tests of loess soils.
Mathematization of individual properties of explosive compaction soils, namely their strength characteristics, is given in the reports on engineering and geological surveys [15]. Adaptation of strength indicators to values for numerical calculations is implemented. Studies on the indicators of specific adhesion and the angle of internal friction of soils compacted by deep blasts using the regression analysis method are performed in [16]. Modeling of the vertical diffusion coefficient of gas in loess soils compacted by blasts is implemented [17]. Regression models of individual physical parameters of soils, such as porosity, permeability, water saturation [18], and filtration depending on pressure [19], are constructed. These studies allow us to evaluate the mechanical-and-physical properties of loess soils after their compaction by deep blasts, but do not describe the specifics of the implementation of the engineering and technology process of loess compaction.
Mathematical modeling of compaction of loess soils by deep hydraulic blasts requires solving individual inverse applied problems — assessing the power of the explosive charge, the depth of its placement, dispersion coordinate changes of gas atoms formed during the blast, in soils, and others. One of these problems sets the objective of this research — mathematical modeling of the power of the explosive charge taking into account the mechanical-and-physical properties of compacted geological systems, their anisotropy and isotropy.
The development of the model will not only improve the quality of compaction, but also reduce the financial costs of implementing the engineering and technology process. Compaction of loess using the proposed model eliminates the stage of trial preliminary blasts at the construction site, which is performed to determine the optimal power of the explosive charge and obtain the required mechanical properties of non-subsiding soils.
The research objective is implemented through mathematical modeling tools (analytically and numerically). Analytical representations will be constructed to estimate the explosive charge power based on the solution to initial boundary value problems with a semi-empirical diffusion equation. The mechanical-and-physical properties of compacted soils will be taken into account. Numerical modeling tools will be used to obtain an estimate of the charge power. Conducting a computational experiment will allow us to establish the adequacy of the proposed solution to the inverse problem to the experimental data.
Materials and Methods. The inverse problem of estimating the power of an explosive charge arises within the framework of mathematical modeling of compaction of subsidence soils by deep blasts. To eliminate the subsidence of loess, the process of their compaction is described by the model based on a given differential semi-empirical diffusion equation. It also takes into account the initial and boundary conditions. The mathematical formulation of the density model of compacted soils has the form [17]:
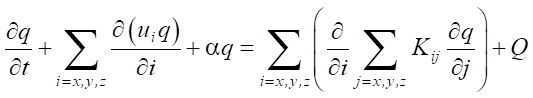 , (1)
, (1)
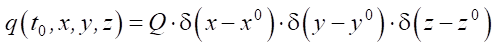 , (2)
, (2)
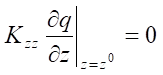 ,
, 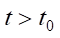 , (3)
, (3)
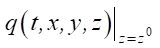 ,
, 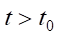 , (4)
, (4)
where q(t, x, y, z) — density of compacted soil during a deep blast at time t; u — parameter of horizontal gas propagation; Kxx, Kyy, Kzz — diffusion coefficients; α — parameter of interaction of gas produced by blast and loess subsidence soil; Q — power of explosive charge (i.e., amount of gas ejected by the charge at time t0 at point (x0, y0, z0)); δ — Dirac delta function.
Initial boundary value problem (1)–(3) corresponds to the process of loess compaction by deep blasts with soil ejection onto the surface. Problem (1), (2), (4) is the compaction of loess without ejection onto the surface. The analytical solutions to problems (1)–(3) and (1), (2), (4) can be represented, respectively, in the form [17]:
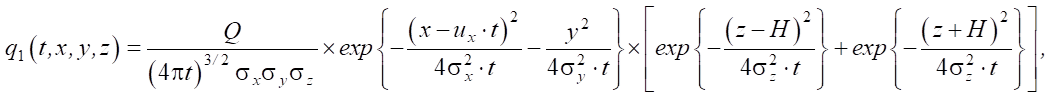 (5)
(5)
 (6)
(6)
In solutions (5) and (6): (0, 0, H) — coordinates of the location of the concentrated explosive charge with power Q = const > 0, acting at the moment of time t0; Н — depth of the explosive charge; 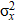 ,
, 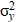 ,
, 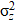 — dispersion changes in the coordinates of gas atoms in the soil.
— dispersion changes in the coordinates of gas atoms in the soil.
Statement of the inverse problem of estimating the power of an explosive charge: let the average values of the soil density and the explosive charges compacted by the method of deep blast be established, corresponding to relations (5) and (6) for cases of soil compaction with and without ejection onto the surface. The value of the depth of the explosive charge Н is known. The value of the dispersion coordinate changes of gas atoms in the soil σ is determined. It is required to estimate the power of the explosive charge Q.
Research Results. We implement solutions to inverse applied problems on the assessment of charge power during compaction of subsiding loess by deep hydraulic blasts based on analytical and numerical methods of mathematical modeling.
According to (5) and (6), two cases are possible: compaction with ejection onto the surface and without ejection. In the first case, based on (5), we obtain the equation:
 (7)
(7)
In the second case, based on (6), we arrive at the equation:
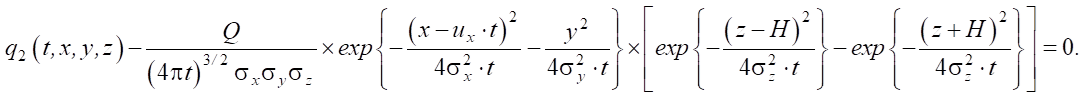 (8)
(8)
For geological systems, the characteristic mechanical-and-physical properties are anisotropy and isotropy.
If the geological system under study is anisotropic, then the filtration properties of the soil depend on the direction of groundwater movement. When implementing soil compaction by blasts with surface ejection, the desired root Q of equation (7) takes the analytical representation:
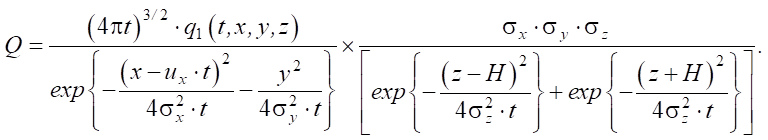 (9)
(9)
If the system under study is isotropic, then the filtration properties of the soil do not depend on the direction of groundwater movement. Let us assume that the dispersion coordinate changes are equal in all directions σz = σy = σx, then, under compacting soils with ejection onto the surface, the desired root Q of equation (7) takes the analytical representation:
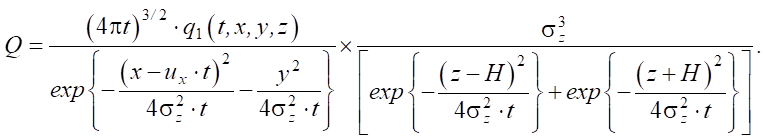 (10)
(10)
Now let us consider the case of soil compaction by deep blasts without ejection onto the surface. If the geological system under consideration is anisotropic, then the desired root Q of equation (8) takes the analytical form:
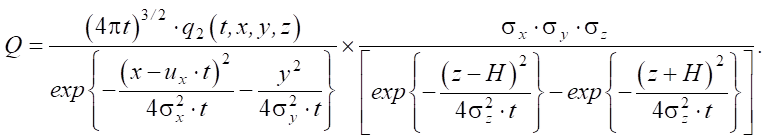 (11)
(11)
If the system under consideration is isotropic, then σz = σy = σx and we can write the required root Q of equation (8) in the form:
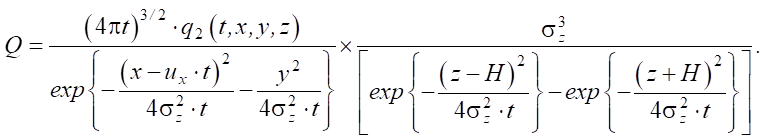 (12)
(12)
Constructed relations (9)–(12) define analytically the power of the explosive charge depending on the mechanical-and-physical properties of the compacted soils and the depth of the charge. To estimate the power values, we use numerical modeling tools.
Computational experiment. We conduct a computational experiment to solve inverse problems arising in the mathematical modeling of loess compaction by deep blasts to provide numeric evaluation of the explosive charge power. The calculations are based on data from a full-scale construction site.
At the construction site “Construction of a Commodity and Raw Material Warehouse”, “Stavrolen” LPG LLC (Budyonnovsk), compaction of subsidence soils [8] with a thickness of 28 m was performed using deep blasts. The total subsidence of the soil under its own weight was from 43 to 78 cm. Groundwater was recorded at a depth of 29–31 m [20]. The average density of dry soil before compaction was 1.43 g/cm³.
At the construction site, drainage blast holes with a diameter of 20 cm were drilled on a cm grid to perform compaction. Charges of water-resistant ammonite weighing 10,000 g were placed in them at a depth of H = 600 cm. A month after compaction, control holes were drilled with the selection of monoliths. The density of dry soil took values in the range from 1.60 g/cm³ to 1.75 g/cm³. The average density of dry compacted soil was 1.66 g/cm³ [8]. Loess refers to soils with a columnar structure and is orthotropic vertically [20]. Taking into account the physical parameters of the soil, we calculate the coefficient of vertical diffusion of gas in soil Kz, according to [17]. Using Kz, we determine the dispersion coordinate changes of gas atoms in the soil, which are equal to σz = 0.726. The parameter of horizontal gas propagation is zero ux = 0. The calculation of the values of the explosive charge power is made according to formula (12). Loess compaction is implemented without ejecting soil onto the surface.
Table 1 presents the result of the assessment of the explosive charge power for known values of compacted soil density, dispersion coordinate changes of gas atoms in the soil, and the depth of the charge. The calculations were conducted using the author's program, developed in the high-level programming language Python, designed to calculate the explosive charge power.
Table 1
Estimated Explosive Charge at Different Values of Compacted Soil Density without Ejection onto the Surface
|
Soil density, g/cm³ |
Estimated explosive charge, g |
|
1.60 |
9797.53 |
|
1.61 |
9809.56 |
|
1.62 |
9815,83 |
|
1.63 |
9836.05 |
|
1.64 |
9876.28 |
|
1.65 |
9936.51 |
|
1.66 |
9996.72 |
|
1.67 |
10046.74 |
|
1.68 |
10094.16 |
|
1.69 |
10114.28 |
|
1.70 |
10137.53 |
|
1.71 |
10159.82 |
|
1.72 |
10186.04 |
|
1.73 |
10208.27 |
|
1.74 |
10228.49 |
|
1.75 |
10243.71 |
Let us analyze the results presented in Table 1. To exclude the property of subsidence and reach the density of dry compacted soil ≥1.60 g/cm³, the power of the explosive charge can take values in the range from 9797.53 to 10243.71 g. According to experimental data, the power of the explosive charge is 10000 g [8]. The absolute error of calculations for soil density values from 1.60 g/cm³ to 1.75 g/cm³ does not exceed 0.244. With an average soil density q = 1.66 g/cm³, the absolute error is 3.28 g.
We consider the compaction of loess with the ejection of soil onto the surface. We calculate the values of the explosive charge power using formula (10) at σz = 0.726 and the density of dry soil from 1.60 g/cm³ to 1.75 g/cm³. The results obtained are presented in Table 2.
Table 2
Estimated Power of Explosive Charge at Different Values of Compacted Soil Density with Ejection onto the Surface
|
Soil density, g/cm³ |
Calculated Explosive Charge, g |
|
1.60 |
9852.18 |
|
1.61 |
9881.62 |
|
1.62 |
9952.77 |
|
1.63 |
10021.13 |
|
1.64 |
10053.84 |
|
1.65 |
10094.28 |
|
1.66 |
10123.92 |
|
1.67 |
10157.54 |
|
1.68 |
10187.62 |
|
1,69 |
10204.75 |
|
1.70 |
10221.83 |
|
1.71 |
10242.25 |
|
1.72 |
10256.89 |
|
1.73 |
10279.34 |
|
1.74 |
10293.79 |
|
1.75 |
10301.24 |
The analysis of the explosive charge power values presented in Table 2 shows that the calculated charge power can take values from 9852.18 g to 10301.24 g. The absolute calculation error does not exceed 0.301. With the average soil density q = 1.66 g/cm³, the absolute error is 123.92 g. The minimum absolute error is 0.02113 at q = 1.63 g/cm³.
Figures 1, 2 show a graphical interpretation of the calculated values of the explosive charge power at different indicators of the density of dry compacted soil and experimental data on the charge power. The charge power values are marked in accordance with the recommendations for compaction of subsidence soils of high power by the hydraulic blasting method1 (solid line). When the explosive charge is placed at the specified depth, its power is equal to 9960 g. Figure 1 shows the case of loess compaction by deep blast without ejection onto the surface, Figure 2 — with ejection onto the surface.
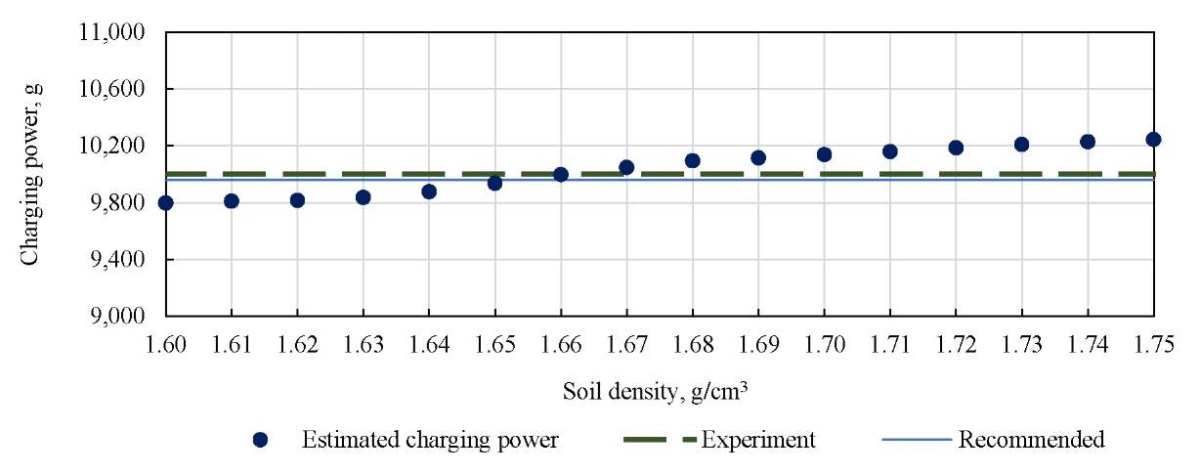
Fig. 1. Estimated and experimental power of explosive charge at different values of soil density without ejection onto the surface
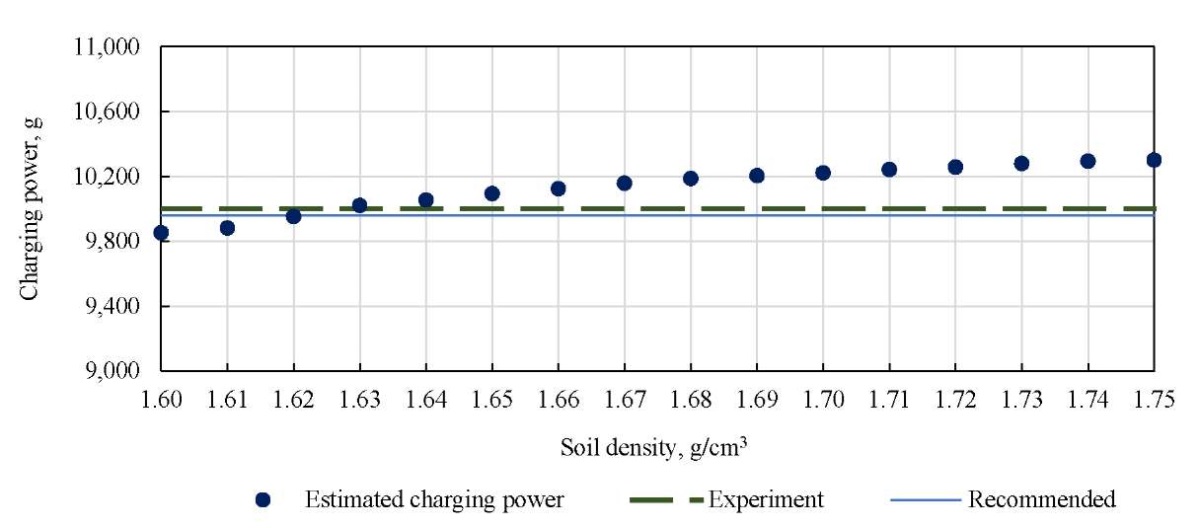
Fig. 2. Estimated and experimental power of explosive charge at different values of soil density with ejection onto the surface
Upon completion of the engineering and technology process of compaction of loess using deep blasts, in accordance with [8], after the discharge of water from the pit, the upper buffer layers of the construction site are further compacted using surface methods.
Discussion. The constructed mathematical model of the explosive charge power is described analytically (9)–(12). The model is intended for performing numerical calculations and assessing the charge power values. The formulas show the nature and degree of dependence of the charge power and the mechanical-and-physical properties of soils, their isotropy and anisotropy. A growth of the charge power entails an increase in soil density, a decrease in subsidence and porosity.
The ideas obtained allowed us to conduct a theoretical experiment on the numerical evaluation of the values of the explosive charge power. The calculated values have an absolute computational error in the intervals: (3.28; 243.71) g — compaction without soil ejection onto the surface, and (21.13; 301.24) g — compaction with soil ejection onto the surface of the construction site.
The disadvantage of the proposed approach is that the density of the compacted loess, the value of the dispersion coordinate changes of gas atoms in the soil are determined on the basis of field and laboratory tests. The depth of the explosive charge is also specified in advance. Thus, when assessing the power of the charge, stamp and compression data will be contained. The proposed model takes into account the isotropy and anisotropy of soils. The results obtained in this study are adequate to the experimental data and confirm the possibility of their practical application in planning the engineering and technology process of compaction of subsidence soils by deep hydraulic blasts.
Conclusion. The main research result is a mathematical model for assessing the power of an explosive charge. Analytical expressions for the power of the charge are obtained. The mechanical-and-physical properties of soils, their isotropy and anisotropy are taken into account. Numerical values of power are found using a program developed in Python. The results obtained are in good agreement with the values of a natural experiment and the recommended values based on empirical data.
The practical significance of the study involves the possibility of using the mathematical model as a calculation method in research and design organizations engaged in theoretical investigation and practical implementation of compaction of subsidence loess soils. Further research will be aimed at constructing solutions through mathematical modeling and other inverse problems within the framework of the engineering and technology process of soil compaction.
1. Recommendations for compaction of high-power subsidence soils using hydraulic blasting. Moscow: Stroiizdat; 1984. 56 p. (In Russ.) URL: https://meganorm.ru/Data2/1/4293782/4293782665.pdf (accessed: 01.06.2025).
References
1. Trofimov VT (ed), Balykova SD, Andreeva TV, Ershova AV, Shaevich YaE. Reference Engineering-Geological Sections of Loess Rocks of Northern Eurasia. Monograph. Moscow: KDU; 2008. 608 p. (In Russ.)
2. Xiaoyu Zhu, Jessica Gray, Ying Gu, Tong He. Genesis of Loess Particles on the Chinese Loess Plateau. Geochemistry, Geophysics, Geosystems. 2022;23(7):e2022GC010428. https://doi.org/10.1029/2022GC010428
3. Torgoev IA, Aleshin YuG. Seismogenic Liquefaction Landslides in Loess-Like Loams. In: Proc. Annual Session of the RAS Scientific Council on the Problems of Geoecology, Engineering Geology and Hydrogeology. “Sergeev Readings. Fundamental and Applied Issues of Modern Soil Science”. Moscow: GeoInfo; 2022. P. 224–229. (In Russ.)
4. Korolev VA, Grigorieva IYu. The Ecological-Geological Systems of Loess Soil Massifs. Engineering Geology World. 2022;ХVII(2):42–64. (In Russ.) https://doi.org/10.25296/1993-5056-2022-17-2-42-64
5. Jianhua Ma, Runqiang Zeng, Xingmin Meng, Zonglin Zhang, Shufen Zhao, Ziran Wei. Field Research on Preferential Infiltration in Rainfall-Induced Loess Landslides. Engineering Geology. 2025;354:108184. https://doi.org/10.1016/j.enggeo.2025.108184
6. Jinduo Yang, Xi-An Li, Lincui Li, Zhang Jing, Weiping Wang. Formation Mechanism of Metastable Internal Support Microstructure in Malan Loess and Its Implications for Collapsibility. Engineering Geology. 2025;346:107892. https://doi.org/10.1016/j.enggeo.2024.107892
7. Shijie Zhai, Guangyin Du, Zhongxun Zhuang, Changhui Gao, Chuanle Wang. Effect of Resonance Compaction Method on the Bearing Capacity Considering Geotechnical Spatial Variability Characteristics. Engineering Geology. 2023;324:107256. https://doi.org/10.1016/j.enggeo.2023.107256
8. Galay BF. Compaction of Subsidence Soils by Deep Explosions. Stavropol: Servisshkola, 2015. 240 p. (In Russ.)
9. Zekun Li, Penghui Ma, Jianqi Zhuang, Qingyi Mu, Jiaxu Kong, Luqing Zhao, et al. Permeability Characteristics, Structural Failure Characteristics, and Triggering Process of Loess Landslides in Two Typical Strata Structures. Engineering Geology. 2024;341:107728. https://doi.org/10.1016/j.enggeo.2024.107728
10. Prokopov AYu, Sychev IV, Ryazantseva A. Determining the Stabilised Subfoudation Soil Deformation Modulus according to the Plate Load Tests and Geotechnical Monitoring Data. Modern Trends in Construction, Urban and Territorial Planning. 2023;2(3):17–30. https://doi.org/10.23947/2949-1835-2023-2-3-17-30
11. Jing Yang, Xirong Niu, Qigao Guo, Zhiheng Wen, Hailong Cao. Strength and Deformation Characteristics of Compacted Loess with Different Moisture Content and Compaction Energy. Results in Engineering. 2023;20:101637. https://doi.org/10.1016/j.rineng.2023.101637
12. Xiaowei Liu, Xudong Zhang, Xiaogang Fu, Tianxiang Yang, Zisong Su. Experimental Study on Creep Characteristics of Saturated Q2 Loess. Frontiers in Earth Science. 2022;10:815275. https://doi.org/10.3389/feart.2022.815275
13. Osipov VI, Sokolov VN, Karpenko FS. Physicochemical Mechanics of Disperse Porous Materials as a New Approach to Assessing Mechanical Stability of Clay Soils. Geology. Engineering Geology. Hydrogeology. Geocryology. 2024;4:50–63. https://doi.org/10.31857/S0869780924040059
14. Karpenko FS. Clayey Soils Properties on the Physicochemical Theory of Strength Positions. Soil Science. 2023;2:3–12. (In Russ.) https://doi.org/10.53278/2306-9139-2023-2-21-3-12
15. Petrakov AA, Prokopov AYu, Petrakova NA, Panasjuk MD. Interpretation of Strength Properties of Soil for Numerical Analyses. Izvestiya TulGU. Sciences of Earth. 2021;1:225–236.
16. Tarasenko ЕО. Mathematical Modeling of the Strength Properties of Lesses by the Method of Correlation-Regression Analysis. International Journal for Computational Civil and Structural Engineering. 2024;20(1):171–181. https://doi.org/10.22337/2587-9618-2024-20-1-171-181
17. Tarasenko EO. Estimation of the Vertical Diffusion Coefficient of Gas in Compacted Soils by Means of Mathematical Modeling. Proceedings of ISP RAS. 2024;36(5):181–190. https://doi.org/10.15514/ISPRAS-2024-36(5)-13
18. Kozhevnikova PV, Kuntsev VE, Dorogobed AN, Motryuk EN. Mathematical Modeling of the Distribution of the Reliability of Petrophysical Parameters in the Construction of a Geological Model. Modern High Technologies. 2021;2:31–37. https://doi.org/10.17513/snt.38490
19. Jingping Wang, Haichun Ma, Jiazhong Qian, Peichao Feng, Xiaohui Tan, Lei Ma. Experimental and Theoretical Study on the Seepage Mechanism Characteristics Coupling with Confining Pressure. Engineering Geology. 2021;291:106224. https://doi.org/10.1016/j.enggeo.2021.106224
20. Galay OB. Budennovsk: Geology and City. Monograph. Stavropol: Stavropolservisshkola, 2022. 318 p. (In Russ.).
About the Author
E. O. TarasenkoRussian Federation
Elena O. Tarasenko, Cand.Sci. (Phys.-Math.), Associate Professor of the Department of Computational Mathematics and Cybernetics
1, Pushkin Str., Stavropol, 355017
ResearcherIDAAB-2396-2021
ScopusID 57194241084
A mathematical model is developed for estimating the charge power during loess compaction using deep blasts. The model takes into account the mechanical-and-physical properties of soils and their isotropy or anisotropy. Analytical formulas are derived for cases with and without soil ejection. The conducted numerical experiment confirms the agreement between the calculations and field data. The model eliminates test blasts and reduces costs in compaction design. The method is applicable to design and survey organizations when planning engineering and technology processes.
Review
For citations:
Tarasenko E.O. Mathematical Modeling of Charge Power Assessment with Exclusion of Loess Subsidence by Deep Hydraulic Blasts. Advanced Engineering Research (Rostov-on-Don). 2025;25(3):233-241. https://doi.org/10.23947/2687-1653-2025-25-3-233-241. EDN: OVUJUV
JATS XML














































