Перейти к:
Математическая модель движения бурового раствора по сетке вибросита
https://doi.org/10.23947/2687-1653-2024-24-3-246-254
EDN: IULDLM
Аннотация
Введение. При бурении нефтяных или газовых скважин порода из забоя выносится на поверхность буровым раствором, который очищается от шлама на первой стадии виброситами. Вибросита оснащаются такой сеткой и создают такие траектории виброколебаний рамы, чтобы с одной стороны — обеспечивать очистку поступающего из устья скважины бурового раствора, а с другой — обеспечивать должную степень очистки. Для корректного подбора номенклатуры сеток нужно надежно определять пропускную способность вибросита в реальных условиях. Это позволит заранее заказать требуемое количество сеток с нужным размером ячеек. Ранее исследования проводились путем просеивания смеси калиброванных гранул на стандартном вибростенде или процеживанием минерального масла через неподвижную сетку. Однако это не в полной мере соответствует реальным условиям просеивания бурового раствора. Целью данной работы было моделирование пропускной способности бурового вибросита в реальных условиях путем расчета движения бурового раствора по вибрирующей сетке с использованием её ранее полученной удельной пропускной способности.
Материалы и методы. При создании математической модели полной пропускной способности бурового вибросита использовалась известная ранее математическая модель течения жидкости в открытом канале и конечномерная аппроксимация в виде последовательности участков из сосредоточенных емкостей, соединенных гидравлическими проводимостями (по аналогии с аппроксимацией электрических длинных линий и протяженных газопроводов методом конечных элементов). Расход течения жидкости над сеткой определялся по закону Шези. При этом площадь сечения потока над сеткой для конкретного участка определялась как среднее арифметическое между начальным и конечным значением высоты бурового раствора на соответствующем участке.
Результаты исследования. Составлена цепная расчетная схема просеивания бурового раствора. На основании материального баланса разработаны математические модели определения пропускной способности и высоты бурового раствора над сеткой: для первого участка сетки и первой узловой точки сетки; для последующих участков сетки и последующих узловых точек сетки; для последнего участка сетки и крайней узловой точки сетки.
Получена математическая модель движения бурового раствора по сетке вибросита, которая вследствие конечномерного представления этого потока по n участкам длины сетки представляет собой систему из n интегральных уравнений, описывающих сосредоточенные емкости, и n – 1 алгебраических уравнений, описывающие перетоки бурового раствора между емкостями.
Обсуждение и заключение. Движение бурового раствора по длине сетки вибросита соответствует движению установившегося неравномерного потока в открытом русле. Однако в первом случае — объемный расход по длине переменный (убывающий до нуля), а во втором случае — постоянный по длине. Поэтому использование только одного дифференциального уравнения установившегося неравномерного потока в открытом русле в данном случае недостаточно.
Полученная математическая модель движения бурового раствора по сетке вибросита является математическим обоснованием для разработки моделирующей программы по определению пропускной способности вибросита для реальных условий его работы, то есть для конкретного бурового раствора, данной сетки или заданной системы приводов вибросита.
Ключевые слова
Для цитирования:
Кичкарь И.Ю. Математическая модель движения бурового раствора по сетке вибросита. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):246-254. https://doi.org/10.23947/2687-1653-2024-24-3-246-254. EDN: IULDLM
For citation:
Kichkar I.Yu. Mathematical Model of Drilling Mud Movement along a Shale Shaker Screen. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):246-254. https://doi.org/10.23947/2687-1653-2024-24-3-246-254. EDN: IULDLM
Введение. Пропускная способность комплекса очистки бурового раствора от шлама циркуляционной системы буровой установки лимитируется расходом циркулирующего бурового раствора, который должен быть очищен должным образом [1]. Под пропускной способностью понимается объем бурового раствора, просеянный сквозь сетку, а в качестве расхода — объем бурового раствора, протекший без просеивания. Вибросито является первым технологическим аппаратом в этом комплексе и осуществляет грубую очистку. Поэтому его пропускная способность в основном определяет пропускную способность всей системы очистки.
Пропускная способность комплекса очистки циркуляционной системы (ЦС) стандартной буровой установки должна превышать производительность бурового насоса и составлять порядка 30–80 л/с. Недостаточная пропускная способность ЦС ограничивает скорость проходки [2].
Циркулирующий буровой раствор поступает на вибросито напрямую из устья скважины по желобу. Здесь нет промежуточных емкостей, поэтому даже если его расход кратковременно превысит пропускную способность вибросита, то буровой раствор по сетке перельется в отвал, что приведет к его потере. Если помощник бурильщика откроет шиберную заслонку, то неочищенный буровой раствор мимо сетки вибросита поступит в емкость. Это крайне нежелательный случай, так как шлам оседает в емкости, не позволяя перекачивать его насосом в пескоотделитель. Это резко снижает степень очистки бурового раствора, что приводит к увеличению затрат на бурение и даже к осложнениям в скважине [2].
Пропускная способность конкретного вибросита во многом определяется размером ячейки сетки, которой оно оснащено. С уменьшением размера ячейки существенно уменьшается пропускная способность вибросита, но повышается степень очистки бурового раствора. На практике для предотвращения пропуска раствора мимо вибросита на нем устанавливают сетку с более крупной ячейкой с большим, но неизвестным запасом по пропускной способности [1].
Реальное измерение пропускной способности вибросита затруднено, т.к. после просеивания через сетку раствор сливается в емкость под виброситом самотеком, не проходя по трубопроводу. Поэтому определение пропускной способности бурового вибросита проводилось косвенными методами.
В работе [2] на основании производственного опыта указаны параметры, изменяющие пропускную способность: увеличение длины сетки, снижение скорости потока, уменьшение угла наклона сетки, изменение направления перемещения частиц, уменьшение амплитуды колебаний сетки, одновременное использование двух последовательных или параллельных сеток. Однако авторы не приводят количественные показатели данных параметров. В работе [3] приведены значения пропускной способности бурового вибросита при работе с различными буровыми растворами, но не приводится общая формула. В1 указывается только формула для расчета изменения пропускной способности. Задача выбора сетки для конкретного случая решена в обзоре коллектива американских инженеров2. Она состоит в том, чтобы выбрать сетку с наименьшей ячейкой, при которой вибросито обладало бы пропускной способностью больше заданной. Для испытаний сеток разработано несколько методов, но все они далеки от условий работы вибросит на буровых установках. Так в стандарте API Recommended practice 13C сетки испытываются или просеиванием смеси калиброванных гранул на стандартном вибростенде или процеживанием минерального масла через неподвижную сетку. В работе [4] сделана попытка на основе уравнения Навье-Стокса аналитически описать движение потока бурового раствора по сетке и процесс просеивания его через сетку. Результаты моделирования не учитывают динамические параметры грохота. Эти параметры учтены в работе [5], но в качестве исследуемого не для бурового раствора, а для угольного шлама. Количество всего удаляемого шлама от общей массы сравнительно невелико [6]. Такая концентрация шлама не оказывает заметного влияния на реологию бурового раствора [3]. Соответственно разделение процесса обезвоживания, приведенное в [7] нецелесообразно. Большая концентрация шлама наблюдается в буровом растворе, выходящего из пескоотделителей и илоотделителей, который очищается на втором вибросите3.
Из всего вышесказанного следует, что определить значение пропускной способности бурового вибросита с помощью теоретических исследований пока не получалось. Поэтому целью данной работы было моделирование полной пропускной способности бурового вибросита на основании проведенных ранее лабораторных экспериментов по определению удельной пропускной способности.
Удельная пропускная способность. Коллективом с участием автора ранее была разработана методика [7], техническое и программное обеспечение для экспериментального определения математической модели удельной пропускной способности конкретной сетки первого вибросита по реальному буровому раствору для конкретного вибросита, проведены экспериментальные исследования [8]. Если у всех точек рамы сита, расположенных по линии сетки, траектории виброколебаний одинаковы, или, как говорят в вибротехнике «траектории однородны», то достаточно провести один эксперимент. Если траектории неоднородны, то достаточно провести три эксперимента при траекториях на краях и в центре сетки. В любом случае параметры виброколебаний точек рамы у производственного вибросита должны быть известны и реализованы в экспериментах.
Известны экспериментальные стенды других ученых, например, в работе [9] описан стенд, который создает полигармонические траектории колебаний. Это достигается соответствующей компоновкой системы привода с кратной частотной вращения. В ходе экспериментов получены даже фигуры Лиссажу [10]. Полученная наилучшая конструкция может работать менее эффективно за счет внешних воздействий. При этом целью автоматического управления является компенсация негативного влияния внешних воздействий. В работе [11] приведен способ управления, в [12] — динамические параметры вибросита в ходе управления, а в [13] приведен пример пошаговой оптимизации с помощью комплексов моделирования Adams и Nastran.
Проведенные эксперименты по просеиванию воднобентонитового раствора плотностью 1,19 г/см3 через образец сетки с квадратными ячейками размером 0,4×0,4 мм позволили получить следующую математическую модель удельной пропускной способности сетки [9]
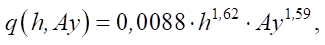 (1)
(1)
где q(h, Ay) — удельная пропускная способность сетки, м3/м2с; h — высота слоя бутового раствора на сетке, м; Ay — амплитуда вертикального виброускорения, м/с2.
Граничные условия процесса просеивания
Наличие математической модели удельной пропускной способности недостаточно для определения пропускной способности бурового вибросита. Необходимо также знание распределения высоты слоя бурового раствора по длине сетки h(x) при известном расходе раствора, поступающего на сетку сита Q(0). Принять в первом приближении линейное распределение высоты по длине сетки не представляется возможным, так как неизвестно граничное условие в конце процесса просеивания h(0) Граничное условие начала процесса просеивания, как было описано ранее, известно и имеет вид h(0,8 ∙ L) = 0, где L — длина сетки, м.
В классической гидравлике известна математическая модель распределения высоты слоя жидкости по длине потока при безнапорном установившемся неравномерном течении жидкости в открытом канале [14]. Однако расход жидкости в этом случае постоянен по длине потока, а в нашем случае расход уменьшается вследствие просеивания части бурового раствора. Следовательно, установившееся движение потока бурового раствора по сетке вибросита представляет собой объект с распределенными по длине сетки переменными h(x) и Q(x).
Методы расчета распределенных объектов
Поиск инженерных решений подобных задач показал, что в электротехнике электрические длинные линии заменяют цепочкой сосредоточенных сопротивлений, емкостей и индуктивностей [15]. Протяженные газопроводы для моделирования их работы заменяют цепочкой перемежающихся емкостей и гидравлических сопротивлений [16]. Особенно часто подобный подход используется в динамике машин, где по чертежам общих видов строятся цепные расчетные схемы, состоящие из перемежающихся сосредоточенных масс или моментов инерции и сосредоточенных податливостей для вибрационных машин [17] и систем управления [18]. Это по сути является конечно-элементной аппроксимацией распределенных объектов.
Построение математической модели полной пропускной способности бурового вибросита
Построим расчетную схему потока бурового раствора из сосредоточенных емкостей и сосредоточенных гидравлических проводимостей, приведенную на рис. 1. Для этого разобьем длину сетки вибросита узловыми точками на равные участки длиной Δx = L/m, где m — число участков. Узловые точки обязательно должны стоять в начале и в конце сетки. В узловые точки поместим сосредоточенные емкости. Начальной и конечной емкости соответствует участок потока длиной 0,5 ∙ Δx, остальным емкостям — Δx.
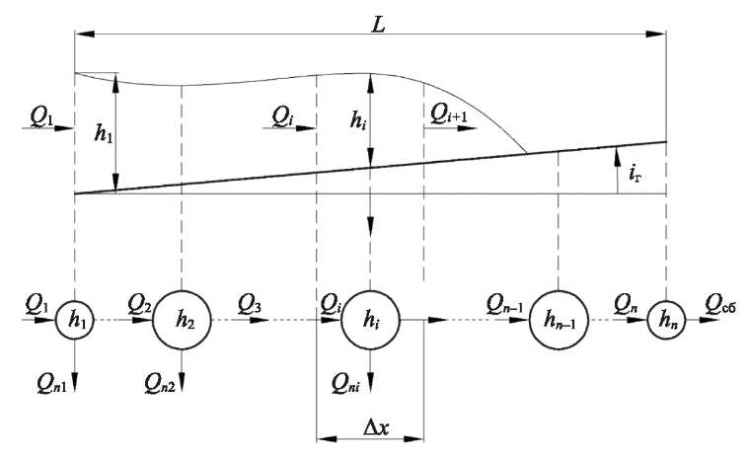
Рис. 1. Цепная расчетная схема
гидравлической системы движения потока бурового раствора по сетке
Уравнение материального баланса для первой емкости на рис. 1 имеет вид:
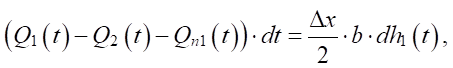 (2)
(2)
где Q1(t) — расход бурового раствора, поступающий на вибросито, м3/с; Q2(t) — расход бурового раствора, вытекающий сетке из емкости 1-й узловой точки в емкость 2-й узловой точки, м3/с; Qn1(t) — расход бурового раствора, просеянный на первом участке, м3/с; h1(t) — высота слоя раствора в первой узловой точке, м;
b — ширина сетки, м.
Просеянный расход в первой узловой точке с учетом удельной пропускной способности равен:
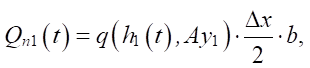 (3)
(3)
где Ay1 — амплитуда виброускорения в первой узловой точке.
Подставив выражение (3) в (2) и преобразовав уравнение, получим выражение для h1(t):
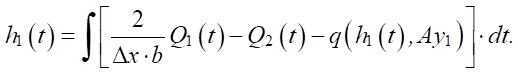 (4)
(4)
Уравнение материального баланса для емкостей всех промежуточных узловых точек на рис. 1 имеет вид:
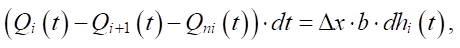 (5)
(5)
где Qi(t) — расход бурового раствора, втекающий в емкость i-той узловой точки, м3/с; Qi+1(t) — расход бурового раствора, вытекающий по сетке из емкости i-й узловой точки в емкость i + 1-й узловой точки, м3/с; Qni(t) = q(hi(t), Ay) ∙ Δx ∙ b — расход бурового раствора, просеянный на i-ом участке, м3/с; hi(t) — высота слоя раствора в i-ой узловой точке, м.
Преобразовав уравнение (5), получим выражение для hi(t) всех промежуточных узловых точек:
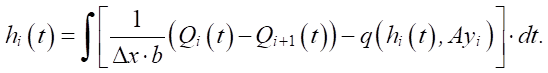 (6)
(6)
В последней узловой точке исходя из физических соображений примем высоту слоя раствора нулевой (С), чтобы не подпирать поток в случае течения его в отвал. Это по сути — правое граничное условие для высоты слоя раствора. Расход бурового раствора, поступающий на вибросито, в данной математической модели принят постоянным и равным заданной величине Q1(t) = Q1 зад. Это косвенное задание левого граничного условия для высоты слоя раствора.
Все промежуточные расходы Qi(t) на рис. 1 определяются перепадом высот слоя раствора hi–1(t) – hi(t) и сосредоточенным гидравлическим сопротивлением участка сетки. Буровой раствор является неньютоновской жидкостью, но при турбулентном течении глинистых растворов можно исходить из обычных формул гидравлики [19].
Для определения расхода Qi(t) не будем определять величину гидравлического сопротивления участка сетки длиной Δx, а воспользуемся известным дифференциальным уравнением установившегося неравномерного потока постоянного расхода [20], но для поднятой сетки:
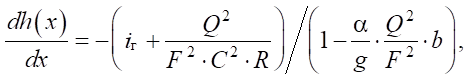 (7)
(7)
где iг — геометрический уклон русла потока, на рисунке 1 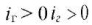 ; F — площадь поперечного сечения потока, м2; C — коэффициент Шези; R — гидравлический радиус сечения потока, м; α — коэффициент Кориолиса, α = 1,10 – 1,15 [21]; g — ускорение свободного падения.
; F — площадь поперечного сечения потока, м2; C — коэффициент Шези; R — гидравлический радиус сечения потока, м; α — коэффициент Кориолиса, α = 1,10 – 1,15 [21]; g — ускорение свободного падения.
Выразим в дифференциальном уравнении (7) производную конечными разностями и подставим в него переменные из расчетной схемы на рис. 1:
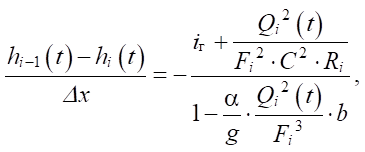 (8)
(8)
где Fi — площадь поперечного сечения потока на участке от i – 1-ой узловой точки до i-ой узловой точки.
Здесь следует уточнить, что Qi(t) — это расход на участке от i – 1-ой узловой точки до i-ой узловой точки. Площадь поперечного сечения потока на этом участке изменяется от величины hi–1(t) b до величины hi(t) b. Поэтому величину Fi будем определять как среднее значение этих площадей:
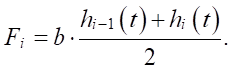 (9)
(9)
Величина гидравлического радиуса потока равна отношению [15]:
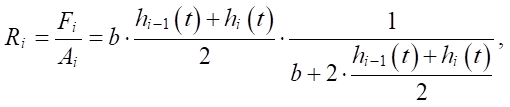 (10)
(10)
где Ai — длина смоченного периметра потока на участке от i – 1-ой узловой точки до i-ой узловой точки, м.
Ширина сетки промышленных вибросит — от 1 метра, толщина слоя раствора на сетке — несколько сантиметров [4]. Поэтому из выражения (10) следует, что Ri ≈ (hi–1(t) + hi(t))/2. Подставив это значение и значение Fi из выражения (9), получим:
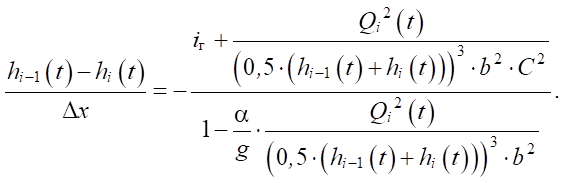 (11)
(11)
Разрешим уравнение (11) относительно Qi(t) для i > 1:
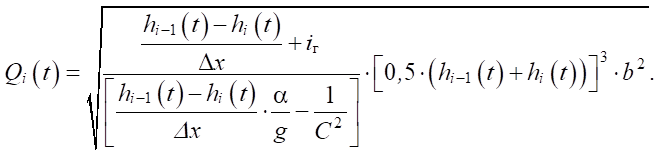 (12)
(12)
Обсуждение и заключение. Математическая модель течения бурового раствора по сетке вибросита представляет собой систему из n уравнений (6) и n – 1уравнений (12).
Начальные условия для переменных hi(0) принять нулевыми нельзя, так как это приведет к делению на ноль в уравнениях (12). Поэтому рекомендуется принять эти условия ненулевыми, но достаточно малыми, например, hi(0) = 0,0001.
Моделирование системы уравнений (6) и (12) можно производить в моделирующих средах, например, MATLAB с приложением Simulink или SimInTech. В любом случае надо определиться с количеством узловых точек цепной расчетной схемы на рис. 1. Пропускная способность вибросита, оснащенного конкретной сеткой, равна расходу Q1 зад, при котором последние 20–25 % длины сетки были бы свободны от бурового раствора и использовались для обезвоживания шлама4. Поэтому предпоследняя узловая точка при минимальном количестве этих точек должна находится на таком же расстоянии от края сетки. Отсюда следует Δx ≈ 0,15 ∙ L, чему соответствует семь узловых точек.
В этой работе стояла задача определения установившегося движения потока бурового раствора, а точнее его профиля. Переходный процесс этого движения автор вынужден был использовать, так как невозможно было установить левое граничное условие h1(∞), вместо которого использовано косвенное задание этого граничного условия Q1(t) = Q1 зад. Окончательное количество узловых точек определится только в процессе моделирования по показателю точности профиля бурового раствора. Для этого производят моделирование математической модели (6) и (12) с n и n + 1 узловыми точками. Если наибольшая разность профилей потока превосходит, например, 5 % от значения высоты слоя раствора в этой точке, то увеличивают число узловых точек на единицу до n + 2 [22]. Затем производят моделирование c n + 2-ми узловыми точками и сравнивают профили потока этого моделирования с результатом предыдущего моделирования с n + 1 точками. По достижению заданной погрешности в дальнейшем используют математическую модель с последним значением количества узловых точек.
Полученная математическая модель движения потока бурового раствора по сетке вибросита совместно с ранее полученной математической моделью удельной пропускной способности сетки по конкретному буровому раствору [8] позволяет обоснованно рекомендовать установку сетки с определенными размерами ячеек для различных расходов бурового раствора, истекающего из устья скважины.
1. American Association of Drilling Engineers Shale Shakers and Drilling Fluid System. Houston: Gulf Publishing Company; 1999. 335 р.
2. Там же. С. 3–335.
3. Там же. С. 3–335.
4. American Association of Drilling Engineers Shale Shakers and Drilling Fluid System. Houston: Gulf Publishing Company; 1999. 335 р.
Список литературы
1. Плетнев Н.С., Семенов Н.В. Анализ типовых конструкций вибрационных сит и особенностей их эксплуатации. В: Материалы Всероссийской конференции с международным участием c элементами научной школы «Современные проблемы гидрогеологии, инженерной геологии и гидрогеоэкологии Евразии». Томск: Издательство ТПУ; 2015. С. 632–635. URL: https://earchive.tpu.ru/bitstream/11683/18336/1/conference_tpu-2015C109-118.pdf (дата обращения: 29.04.2024).
2. Булатов А.И., Проселков Ю.М., Шаманов С.А. Техника и технология бурения нефтяных и газовых скважин. Москва: Недра; 2003. 1007 с. URL: https://www.geokniga.org/bookfiles/geokniga-bulatov-ai-proselkovyum-shamanov-sa-tehnika-i-tehnologiya-bureniya-neftyanyh-i-.pdf (дата обращения: 20.05.2024).
3. Рязанов А.Я. Энциклопедия по буровым растворам. Оренбург: Летопись; 2004. 664 с. URL: https://www.geokniga.org/bookfiles/geokniga-enciklopediyapoburovymrastvoram.pdf?ysclid=lwyzjxbik6960660361 (дата обращения: 20.05.20204).
4. Сансиев В.Г. Гидродинамические основы процесса ситовой очистки бурового раствора. Известия высших учебных заведений. Нефть и газ. 2009;75(3):41–46.
5. Сансиев В.Г. Моделирование процессов классификации и обезвоживания угольного шлама на сите грохота. Горный информационно-аналитический бюллетень. 2013;(7):325–335.
6. Головин М.В., Добик А.А., Кортунов А.В., Мищенко В.И. Современные тенденции развития вибросит для очистки буровых растворов. Бурение и нефть. 2014;(3):50–52. URL: https://burneft.ru/archive/issues/2014-03/14 (дата обращения: 20.05.2024).
7. Кичкарь Ю.Е., Кичкарь И.Ю., Миллер А.С. Способ определения удельной пропускной способности сеток вибросит. Патент РФ, № 2379127 C 1. 2010. 8 с. URL: https://patents.s3.yandex.net/RU2379127C1_20100120.pdf (дата обращения: 20.05.2024).
8. Кичкарь Ю.Е., Кичкарь И.Ю. Исследование влияния параметров колебаний рамы на удельную пропускную способность вибросита. Автоматизация, телемеханизация и связь в нефтяной промышленности. 2017;(8):37–40.
9. Penagos HP, Gantiva ME, López JAA. Detection of Failures in the Operation of Shale Shaker Machines for the Separation of Solids In: Proc. 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME). New York City: IEEE; 2023. P. 1–6. https://doi.org/10.1109/ICECCME57830.2023.10253357
10. Zhipeng Lyu, Sizhu Zhou. Design of Spatial Lissajous Trajectory Vibrating Screen. In book: Jianrong Tan (ed). Advances in Mechanical Design. Singapore: Springer; 2020. P. 493–498. https://doi.org/10.1007/978-981-32-9941-2_40
11. Кичкарь И.Ю., Кичкарь Ю.Е., Посмитная Л.А. Способ управления системой приводов вибросита. Патент РФ, № 2649203. 2018. 14 с. URL: https://patents.s3.yandex.net/RU2649203C1_20180330.pdf (дата обращения: 20.05.2024).
12. Osadolor AO, Bashir ME, Osifo TI. Development and Evaluation of a Small-Scale Shale Screening Machine. Nigerian Journal of Scientific Research. 2022;21(1):72–78.
13. Korostelkin AA, Filintsev AA, Novokshonov VV, Nikitin AV. On Shale Shaker’s Structural Optimization and Performance Improvement. IOP Conference Series: Materials Science and Engineering. 2020;986(1):012058. https://doi.org/10.1088/1757-899X/986/1/012058
14. Калинин А.В. Зависимость коэффициента Шези от числа Фруда. Вестник науки и образования Северо-Запада России. 2019;5(3):38–56.
15. Васильева Т.Н., Аронов Л.В. Математическая модель режимов работы распределительной электрической сети значительной протяженности. Вестник Рязанского государственного агротехнологического университета имени П.А. Костычева. 2012;14(2):51–54. URL: https://vestnik.rgatu.ru/archive/2_2012.pdf?ysclid=lwz0apyfjj690751007 (дата обращения: 20.05.2024).
16. Мешалкин В.П., Чионов А.М. Компьютерное моделирование протяженных многослойно изолированных подводных газопроводов высокого давления. Математическое моделирование. 2017;29(8):110–122. URL: https://www.mathnet.ru/links/b0a80e5d714ee1ef962f28050fffa21f/mm3880.pdf (дата обращения: 20.05.2024).
17. Блехман И.И. Теория вибрационных процессов и устройств. Вибрационная механика и вибрационная техника. Санкт-Петербург; Издательский дом «Руда и металлы»: 2013. 640 с.
18. Куликов В.О., Брейдо И.В. Пропуск резонансных частот вибрационного грохота с использованием преобразователячастоты Mitsubishi Electric FR серии A800. Наука настоящего и будущего. 2019;1:222–226. URL: http://elib.kstu.kz/fulltext/temat/2019/elibrary_41177383_25140206.pdf (дата обращения: 20.05.2024).
19. Булатов А.И. Системный анализ исследований течения вязко-пластичных жидкостей – глинистых и цементных растворов (ч. 1). Бурение и нефть. 2016;(3):18–23. URL: https://burneft.ru/archive/issues/2016-03/18 (дата обращения: 20.05.2024).
20. Байгалиев Б.Е., Гортышов Ю.Ф., Самойленко А.В. Исследование влияния откосов на гидравлические сопротивления трапецеидальных русел. Вестник Казанского государственного технического университета им. А.Н. Туполева. 2012;(2):35–43.
21. Абдюкова Р.Я., Хабибуллин М.Я. Расчет геометрических размеров клапана бурового насоса и определение высоты подъема тарели. Оборудование и технологии для нефтегазового комплекса. 2015;(5):15–18.
22. Меретуков З.А., Заславец А.А., Кошевой Е.П., Косачев В.С. Методы решения дифференциальных уравнений гидродинамики. Новые технологии. 2012;(1):36–41.
Об авторе
И. Ю. КичкарьРоссия
Илья Юрьевич Кичкарь, кандидат технических наук, доцент кафедры автоматизации производственных процессов института компьютерных систем и информационной безопасности
350072, г. Краснодар, ул. Московская, 2
Рецензия
Для цитирования:
Кичкарь И.Ю. Математическая модель движения бурового раствора по сетке вибросита. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):246-254. https://doi.org/10.23947/2687-1653-2024-24-3-246-254. EDN: IULDLM
For citation:
Kichkar I.Yu. Mathematical Model of Drilling Mud Movement along a Shale Shaker Screen. Advanced Engineering Research (Rostov-on-Don). 2024;24(3):246-254. https://doi.org/10.23947/2687-1653-2024-24-3-246-254. EDN: IULDLM
JATS XML














































