Scroll to:
Experimental Study of the Kinematics of a Double-Row Planetary Mechanism Using Two Elliptical External Gears
https://doi.org/10.23947/2687-1653-2024-24-4-360-368
EDN: BSOKNM
Abstract
Introduction. Mechanisms with non-circular gears are of wide interest to researchers and inventors due to their compactness and the implementation of a wide range of transfer functions. The development of this area is stimulated by the advancements and reduction in cost of mechanical processing and additive manufacturing technologies, as well as the use of applied mathematical modeling packages for the analysis and synthesis of non-circular gears. Traditionally, noncircular gears are used to transmit rotational motion between parallel axes with a variable ratio of angular velocities. However, their use in planetary gear schemes provides implementing various types of output link motion. The analysis of the papers on the research area shows that gears with movable rotation axes have not been sufficiently studied from the point of view of kinematics and dynamics. Most research papers reveal the theory of such mechanisms without verifying the results obtained in practice. This work is aimed at the experimental verification of the kinematics of a planetary mechanism with two external engagements, which contains elliptical gears.
Materials and Methods. The kinematic model of the mechanism under study is built on the basis of the velocity diagram of its links, which made it possible to obtain expressions for finding an analogue of the angular velocity and the position function of the output shaft. The experimental study of kinematics was performed on a laboratory stand containing a model of a planetary mechanism with a set of replaceable gear wheels, absolute encoders on the input and output shafts of the mechanism, a controller, and a PC for recording and processing the signal. The analysis of the obtained results was performed on a computer using statistical analysis methods.
Results. As a result of kinematic analysis, position functions were constructed for three alternative planetary mechanisms, which had different geometric parameters of the gears and made it possible to implement various types of motion of the output shaft: swinging motion, discontinuous motion, and unilateral uneven rotation.
Discussion and Conclusion. The analysis of the experimental results showed the adequacy of the constructed mathematical model of kinematics to real mechanisms. The confidence interval of measuring errors at a reliability level of 95% was 0.16±0.08° for the first version of the mechanism, 0.57±0.22° — for the second version, and 0.08±0.26° — for the third. The proposed planetary mechanism with elliptical gears for implementing various types of motion can be used in drives of process equipment in numerous industries: chemical and food (mixers), oil refining (pumping units for crude production), mechanical engineering (compressors, pumps, automated machines), and others. The conducted kinematic studies of the planetary mechanism and their experimental analysis are needed for further dynamic and force investigations, as well as for the design of drives based on the proposed transmission.
Keywords
For citations:
Prikhodko A.A., Belina N.N., Novitskiy A.V., Shchetinin M.M. Experimental Study of the Kinematics of a Double-Row Planetary Mechanism Using Two Elliptical External Gears. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):360-368. https://doi.org/10.23947/2687-1653-2024-24-4-360-368. EDN: BSOKNM
Introduction. Mechanisms with non-circular gears have been known for a long time, but their experimental research and practical implementation have long been difficult due to the focused specialization of such mechanisms, the complexity and high cost of their manufacture. Nowadays, there is an increase in the interest of researchers in this topic. At the same time, most scientific papers on designing non-circular gearing are based on the analysis of geometry [1] and kinematics [2] to obtain the required transfer function for practical application [3]. In [4] and [5], mechanisms for synthesizing angular velocity functions were developed and studied. Researchers proposed robotics with non-circular gears, for example, a jumping robot [6], a hexapod robot [7], an exoskeleton mechanism for knee joint rehabilitation [8]. More efficient planting machines for the agricultural industry were studied from the point of view of kinematics [9] and dynamics [10]. Other numerous devices were developed and designed.
A review of sources has shown that the most common gears are those with an elliptical centrode [11][12]. Machines [10] and devices [4] with elliptical gears are created, the geometry [13] is studied, and some design [14] and manufacturing issues are resolved [15].
Elliptical gears are mainly used to transmit rotary movement between parallel fixed axes [16]. However, such use of non-circular gears allows for only one-way nonuniform rotary movement, which limits the scope of their application. Planetary gears have broader capabilities for implementing complex types of movement of working bodies. The creation of drives based on them will provide the development and implementation of more efficient and compact machines for various technological purposes.
Based on the results of the analysis of scientific literature in the field of transmissions with non-circular gears, a planetary mechanism with elliptical wheels is proposed as an object of study. The objective of the work is an experimental kinematic analysis of a planetary transmission. It is justified by the need to verify theoretical provisions for their correct use at the following stages of design — in dynamic, force analysis and strength calculations.
Materials and Methods. The kinematic model of the mechanism is constructed on the basis of the velocity diagram of its links (Fig. 1).
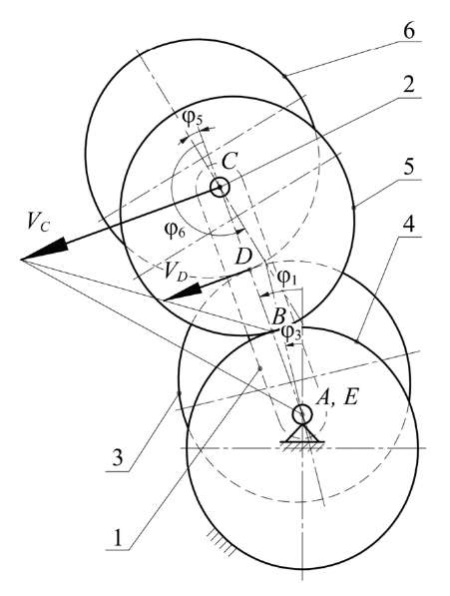
Fig. 1. Velocity diagram for the mechanism under consideration: 1 — carrier; 2 — satellite shaft; 3 — elliptical gear on the output shaft; 4 — sun elliptical wheel; 5, 6 — elliptical wheels of the satellite
The analog of the angular velocity of the output shaft is determined as follows [17]:
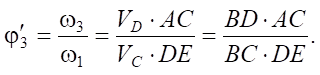 (1)
(1)
Segments BD, BC and DE are determined through the polar equation of the ellipse [17]:
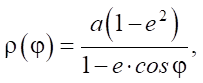 (2)
(2)
where 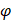 — rotation angle, e and a — eccentricity and semi-major axis of an ellipse.
— rotation angle, e and a — eccentricity and semi-major axis of an ellipse.
We determine the engagement radii of gears 5 and 6:
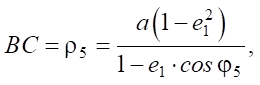 (3)
(3)
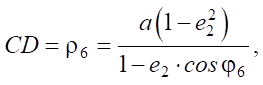 (4)
(4)
where e1 and e2 — eccentricities for each pair of elliptical gears, whose rotation angles 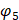 and
and 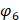 are obtained as follows:
are obtained as follows:
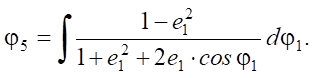 (5)
(5)
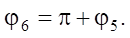 (6)
(6)
Based on the velocity plan and taking into account equations (3), (4), we define the required segments as:
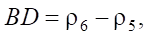 (7)
(7)
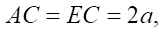 (8)
(8)
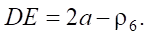 (9)
(9)
Based on (2)–(9), we obtain an expression for determining the analogue of the angular velocity of the output shaft:
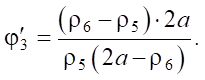 (10)
(10)
The rotation angle is determined by integrating equation (10) over joint coordinate 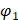 :
:
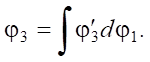 (11)
(11)
Variations of the kinematic scheme of the mechanism include replacing elliptical gears with cylindrical ones in one of the pairs, for the study of which it is required to replace the radius functions with fixed values in the resulting mathematical model.
We consider mechanisms with a pair of elliptical gears 3–6 (e=0.28), and cylindrical wheels 4 and 5 of the following sizes:
- option 1: R5=25 mm, R4=25 mm;
- option 2: R5= 18 mm, R4= 32 mm;
- option 3: R5= 16 mm, R4= 34 mm.
Figure 2 shows the graphs of the position functions obtained using (11).
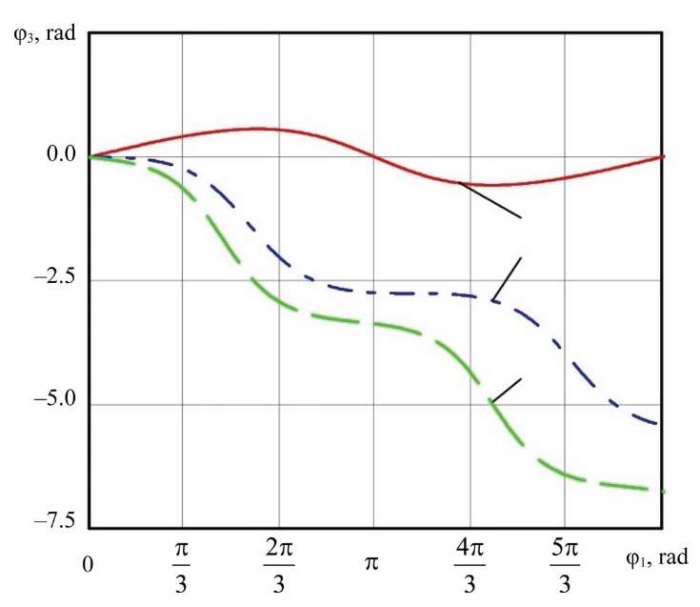
Fig. 2. Dependence graphs for the studied mechanism configurations
The analysis of the graphs shows (in Fig. 2, numbers indicate studied options) that changing the sizes of the gear wheels allows obtaining different types of output shaft movement: reciprocating-rotational (option 1), discontinuous (option 2) and one-way nonuniform rotational movement (option 3).
Research Results. The kinematic analysis confirmed the implementation of various transfer functions, and changing the sizes of gear wheels allows for the kinematic synthesis of new mechanisms.
The object of the experimental study is a prototype, whose details are shown in Figure 3.

Fig. 3. Details of the prototype under study
Rotation angles are measured by absolute encoders (Table 1).
Table 1
Encoder Characteristics
|
Diameter |
Output signal |
Resolution |
Linearity |
Reading speed |
|
22 mm |
0–5 V |
360°/4096≈0.088° |
0.3% |
0.6 ms |
The signal is registered by the Arduino controller and processed on the PC (Fig. 4).
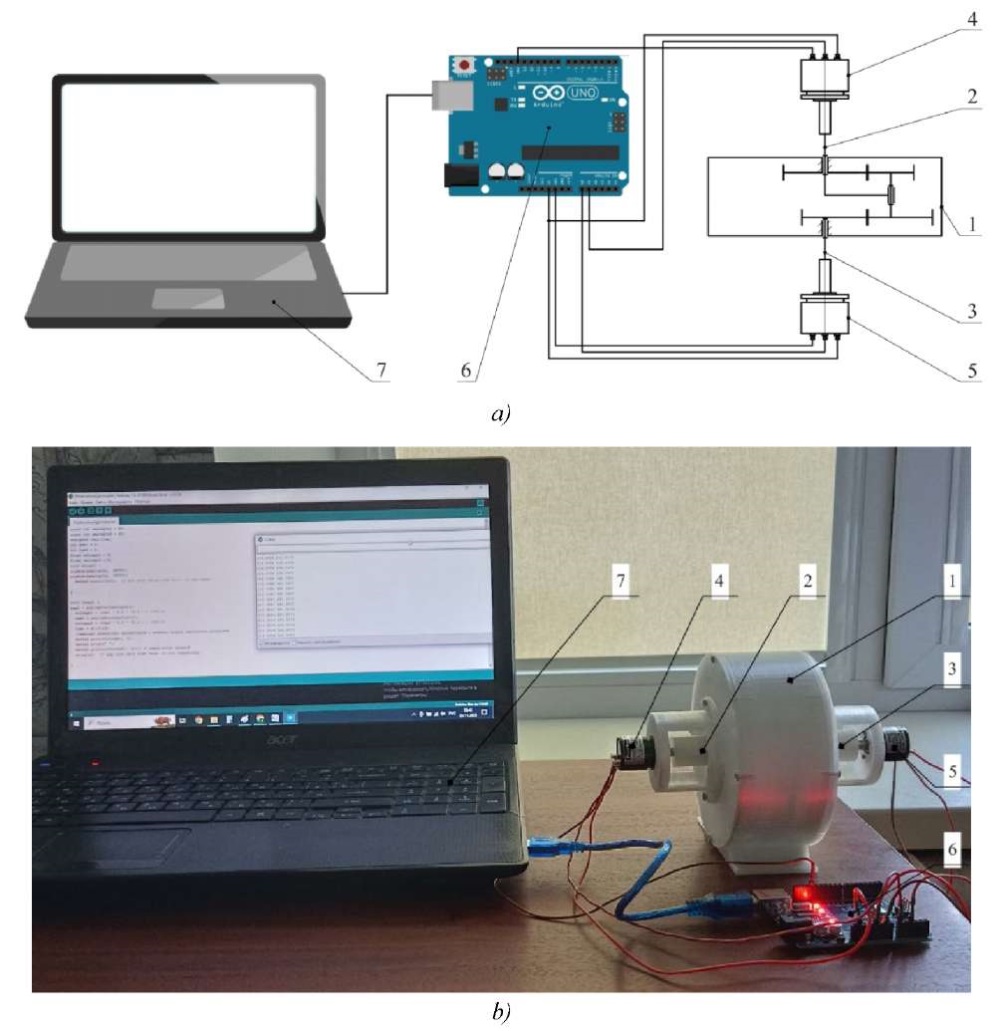
Fig. 4. Schematic diagram (a) and external view (b) of the experimental stand: 1 — housing; 2 — input shaft; 3 — output shaft; 4, 5 — encoders; 6 — Arduino controller; 7 — personal computer
The processing and analysis of the measurement results were performed in the MathCAD application package. The schemes of the studied options and the experiment results are shown in Figure 5.
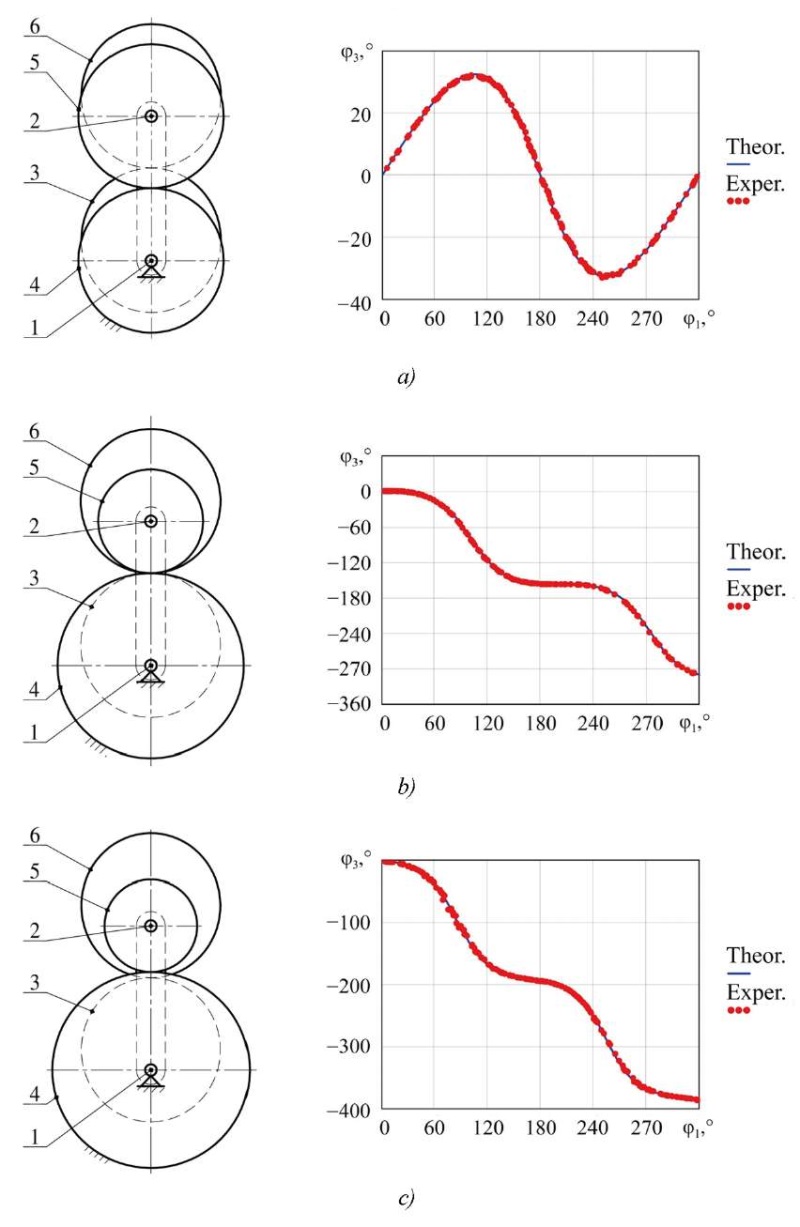
Fig. 5. Research results: a — option 1; b — option 2; c — option 3
As can be seen from the graphs, the measured values of the output shaft rotation angles are adequate to the constructed model. Let us evaluate the results of the experiment using statistical analysis tools.
We determine the average value of measurement errors [18]:
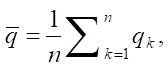 (12)
(12)
where n — number of independent observations qk.
Let us calculate the sample variance:
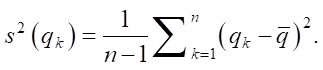 (13)
(13)
An estimate of the dispersion of the mean value is obtained as follows:
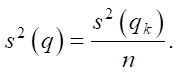 (14)
(14)
The standard uncertainty of Type A measurements is determined [19]:
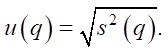 (15)
(15)
Taking the measurement errors as values qk and processing them according to (12)–(15), we calculate the measurement uncertainty. The results of the statistical analysis are given in Table 2.
Table 2
Statistical Analysis of Measurement Errors
|
Mechanism number |
Number of measured values |
Mean error value |
Uncertainty of measurement |
|
1 |
195 |
–0.16° |
0.04° |
|
2 |
168 |
0.57° |
0.11° |
|
3 |
192 |
0.08° |
0.13° |
The confidence interval is defined as 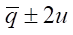 for a level of certainty of 95% and is –0.16 ± 0.08° (option 1), 0.57 ± 0.22° (option 2), 0.08 ± 0.26° (option 3). Thus, the constructed mathematical model of kinematics is adequate to the physical prototypes.
for a level of certainty of 95% and is –0.16 ± 0.08° (option 1), 0.57 ± 0.22° (option 2), 0.08 ± 0.26° (option 3). Thus, the constructed mathematical model of kinematics is adequate to the physical prototypes.
Discussion and Conclusion. A planetary gear with elliptical wheels is presented, providing the implementation of nonuniform, discontinuous and reciprocating-rotational movement of the output shaft. The type of movement is determined by the parameters of the gear wheels.
A kinematic model of the transmission was constructed, and the law of movement of the output shaft was obtained. The analysis of mechanisms with different parameters of gear wheels showed the feasibility of a wide range of transmission functions and types of movement of the output shaft.
The correspondence of the results of the conducted kinematic analysis to real mechanisms is confirmed by an experimental study of the output shaft position functions for three options of the physical prototype. The performed assessment of the adequacy of the mathematical model provides its using in dynamic and force analysis of machines based on the proposed transmissions. The studied options of the mechanism can be used in drives of compact and easy-to-balance technological machines.
References
1. Lozzi A. Non-Circular Gears — Graphic Generation of Involutes and Base Outlines. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2000;214(3):411–422. https://doi.org/10.1243/0954406001523074
2. Qifeng Gao, Jun Ye, Can Liu. Design and Modeling of Noncircular Gear with Curvature Radius Function. Journal of Computational Methods in Sciences and Engineering. 2018;18(3):683–693. https://doi.org/10.3233/JCM-180819
3. Čavić D, Čavić M, Penčić M, Dorić J, Rackov M. IC Engine: Increasing Efficiency by Using Epicyclic Non-Circular Gear Train. In book: Lovasz EC, Maniu I, Doroftei I, Ivanescu M, Gruescu CM. (eds) New Advances in Mechanisms, Mechanical Transmissions and Robotics. Cham: Springer; 2020. P. 391–402. https://doi.org/10.1007/978-3-030-60076-1_36
4. JY Liu, SL Chang, D Mundo. Study on the Use of a Non-Circular Gear Train for the Generation of Figure-8 Patterns. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2006;220(8):1229–1236. https://doi.org/10.1243/09544062JMES268
5. Ottaviano E, Mundo D, Danieli GA, Ceccarelli M. Numerical and Experimental Analysis of Non-Circular Gears and Cam-Follower Systems as Function Generators. Mechanism and Machine Theory. 2008;43(8):996–1008. https://doi.org/10.1016/j.mechmachtheory.2007.07.004
6. Okada M, Takeda Y. Synthesis and Evaluation of Non-Circular Gear that Realizes Optimal Gear Ratio for Jumping Robot. In: Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems. New York City: IEEE; 2013. P. 5524–5529. https://doi.org/10.1109/IROS.2013.6697157
7. Ke-Jung Huang, Shen-Chiang Chen, Haldun Komsuoglu, Gabriel Lopes, Jonathan Clark, Pei-Chun Lin. Design and Performance Evaluation of a Bio-Inspired and Single-Motor-Driven Hexapod Robot with Dynamical Gaits. Journal of Mechanisms and Robotics. 2015;7(3):031017. https://doi.org/10.1115/1.4029975
8. Terada H, Zhu Y, Suzuki M, Cheng C, Takahashi R. Developments of a Knee Motion Assist Mechanism for Wearable Robot with a Non-Circular Gear and Grooved Cams. In book: Lovasz EC, Corves B. (eds) Mechanisms, Transmissions and Applications. Dordrecht: Springer; 2012. P. 69–76. https://doi.org/10.1007/978-94-007-2727-4_6
9. Guo LS, Zhang WJ. Kinematic Analysis of a Rice Transplanting Mechanism with Eccentric Planetary Gear Trains. Mechanism and Machine Theory. 2001;36(11–12):1175–1188. https://doi.org/10.1016/S0094-114X(01)00052-0
10. Zhao Y, Yu GH, Wu CY. Circuit Simulation and Dynamic Analysis of a Transplanting Mechanism with Planetary Elliptical Gears. Transactions of the ASABE. 2011;54(4):1179–1188. https://doi.org/10.13031/2013.39016
11. Wunderlich W. Contribution to the Geometry of Elliptic Gears. Mechanism and Machine Theory. 1975;10(4):273–278. https://doi.org/10.1016/0094-114X(75)90072-5
12. Shinn-Liang Chang, Chung-Biau Tsay, Long-Iong Wu. Mathematical Model and Undercutting Analysis of Elliptical Gears Generated by Rack Cutters. Mechanism and Machine Theory. 1996;31(7):879–890. https://doi.org/10.1016/0094-114X(95)00121-E
13. Biing-Wen Bair. Computerized Tooth Profile Generation of Elliptical Gears Manufactured by Shaper Cutters. Journal of Materials Processing Technology. 2002;122(2–3):139–147. https://doi.org/10.1016/S0924-0136(01)01242-0
14. Yazar M. Design, Manufacturing and Operational Analysis of Elliptical Gears. International Journal of Precision Engineering and Manufacturing. 2021;22(8):1441–1451. https://doi.org/10.1007/s12541-021-00549-3
15. Thai Hong Nguyen. Shaping the Tooth Profile of Elliptical Gear with the Involute Ellipse Curve. VNUHCM Journal of Engineering and Technology. 2021;4(3):1048–1056. https://doi.org/10.32508/stdjet.v4i3.820
16. Litvin FL. Non-Circular Gears. Moscow-Leningrad: MASHGIZ; 1956. 218 p. (In Russ.).
17. Prikhod’ko AA, Smelyagin AI. Kinematics of a Planetary Train with Elliptical Gears with Internal Gearing. Journal of Machinery Manufacture and Reliability. 2021;50(5):412–418. https://doi.org/10.3103/S1052618821050095
18. Hall BD, White DR. An Introduction to Measurement Uncertainty. Lower Hutt: Measurement Standards Laboratory of New Zealand; 2020. 50 p. https://doi.org/10.5281/zenodo.3872590
19. Barash VYa. Uncertainty and Error in Modern Metrology. Legal and Applied Metrology. 2009;105(5):15–20. (In Russ.)
About the Authors
A. A. PrikhodkoRussian Federation
Alexander A. Prikhodko, Cand.Sci. (Eng.), Associate Professor of the Department of Technical Mechanics and Special Machines named after Professor A.A. Petrik
2, Moskovskaya Str., Krasnodar, 350072
N. N. Belina
Russian Federation
Nataliya N. Belina, Cand.Sci. (Eng.), Associate Professor of the Department of Technical Mechanics and Special Machines named after Professor A.A. Petrik
2, Moskovskaya Str., Krasnodar, 350072
A. V. Novitskiy
Russian Federation
Andrey V. Novitskiy, postgraduate student of the Department of Technical Mechanics and Special Machines named after Professor A.A. Petrik
2, Moskovskaya Str., Krasnodar, 350072
M. M. Shchetinin
Russian Federation
Maksim M. Shchetinin, student of the Department of Technical Mechanics and Special Machines named after Professor A.A. Petrik
2, Moskovskaya Str., Krasnodar, 350072
Review
For citations:
Prikhodko A.A., Belina N.N., Novitskiy A.V., Shchetinin M.M. Experimental Study of the Kinematics of a Double-Row Planetary Mechanism Using Two Elliptical External Gears. Advanced Engineering Research (Rostov-on-Don). 2024;24(4):360-368. https://doi.org/10.23947/2687-1653-2024-24-4-360-368. EDN: BSOKNM













































