Preview

User

Not a user? Register with this site Forgot your password?

Advanced Engineering Research (Rostov-on-Don)

Advanced search

Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control for Robotic Manipulators

https://doi.org/10.23947/2687-1653-2025-25-4-2209

EDN: OZLBEC

Contents

Scroll to:

Abstract

Introduction. Robotic manipulators operate in dynamic environments under uncertainties, external disturbances, and actuator faults, posing a critical challenge to their control design. While traditional control strategies, such as PID or computed torque control, offer simplicity, they often lack robustness to unmodeled dynamics. The development of robust and practically implementable control algorithms is becoming increasingly important with the growing use of manipulators in dangerous, precise and ultra-fast operations (industrial automation, medicine, space and service robots). Conventional PID controllers and torque calculation methods are simple but not robust enough to handle unmodeled effects. Sliding Mode Control (SMC), particularly the Super-Twisting variant (STA), provides strong robustness, but suffers from chattering and typically requires prior knowledge of system bounds. Recent advancements like Adaptive Global Integral Terminal Sliding Mode Control (AGITSMC) improve finite-time convergence but may result in overestimated control gains and residual switching effects. This research addresses a critical gap in current methods: the lack of a unified control approach that ensures finite-time convergence, suppresses chattering, and compensates for both unknown disturbances and actuator faults using observer feedback. The objective of this work is to design and analyze an Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control (OFASTSMC) framework that adaptively adjusts its gains, estimates disturbances online, and guarantees smooth, robust performance even in the presence of severe nonlinearities and faults. The objective of this study is to develop and analyze an Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control (OFASTSMC) framework that unifies finitetime observer feedback, adaptive gain tuning, and reinforced sliding surfaces to achieve robust trajectory tracking of robotic manipulators under disturbances and actuator faults, while effectively minimizing chattering and ensuring practical implementability.

Materials and Methods. This study considers the standard dynamic model of an 𝑛𝑛-DOF robotic manipulator derived using Lagrangian mechanics. The model accounts for nonlinear coupling effects, viscous friction, external disturbances, and additive actuator faults. To achieve robust finite-time control, a reinforced sliding surface is constructed using nonlinear error terms with adaptive power exponents, which accelerates error convergence. A finite-time extended state observer (ESO) is incorporated to estimate lumped disturbances and actuator fault torques in real time. Based on these estimates, the control law integrates a super-twisting sliding mode algorithm with adaptive gain tuning and boundarylayer smoothing to reduce chattering while ensuring strong robustness. The closed-loop system stability is formally analyzed within a Lyapunov framework, where rigorous proofs confirm finite-time convergence of the tracking error under the proposed controller. The proposed OFASTSMC algorithm is implemented in MATLAB/Simulink and validated on a 2-DOF planar robotic manipulator. The manipulator is subjected to time-varying disturbances and actuator degradation scenarios. For benchmarking, the method is directly compared with AGITSMC, using identical initial conditions, model parameters, and reference trajectories to ensure a fair and consistent performance evaluation.

Results. Simulation results demonstrate that the proposed OFASTSMC method significantly outperforms the benchmark AGITSMC in terms of tracking precision, robustness, and control smoothness. Specifically, the maximum joint position errors were reduced by over 40% compared to AGITSMC, and the settling time to reach the desired trajectory was shortened by approximately 25%. Additionally, the proposed method effectively mitigated chattering in the control signal due to the use of saturation functions and gain limits, resulting in smoother actuator commands. The adaptive observer accurately estimated the lumped disturbance and fault inputs in real time, providing effective fault compensation without prior knowledge. These improvements were validated across multiple scenarios including abrupt actuator failures, nonlinear load torques, and varying trajectory speeds. The sliding surface convergence was achieved in finite time, confirming the theoretical guarantees of the method.

Discussion. The results validate that OFASTSMC achieves robust, high-precision tracking for robotic manipulators operating under real-world uncertainties. Its novelty lies in the integration of adaptive exponent tuning, finite-time observer feedback, and gain-limited super-twisting control into a unified and practical framework. Unlike previous methods that rely on fixed gain structures or ignore observer feedback, OFASTSMC adapts in real-time and maintains finite-time convergence guarantees with minimal chattering.

Conclusion. The results obtained confirm that OFASTSMC is an efficient and robust solution to the trajectory tracking problem in the presence of uncertainties. The method is computationally efficient and easy to implement in digital control systems, making it suitable for practical deployment in industrial robots, service manipulators, or surgical arms. Future research will focus on extending this method to task-space control and real hardware implementation under sensor noise and model mismatches.

Keywords


robotic manipulators; finite-time stability; super-twisting algorithm; sliding mode control; actuator fault; adaptive control; observer-based control

For citations:

Long H.D. Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control for Robotic Manipulators. Advanced Engineering Research (Rostov-on-Don). 2025;25(4):337-349. https://doi.org/10.23947/2687-1653-2025-25-4-2209. EDN: OZLBEC

Introduction. Robotic manipulators play a pivotal role in modern industries such as manufacturing, logistics, minimally invasive surgery, space exploration, and service robotics [1–3]. Their widespread deployment in safety-critical tasks requires not only high-precision trajectory tracking but also resilience against uncertainties, actuator degradation, and time-varying disturbances [4–6]. With the growing complexity of Industry 4.0 systems and the rise of human–robot collaboration, the demand for robust and adaptive control solutions has become more pressing than ever [7–9].

Classical control methods, such as PID and computed torque control, are widely used for their simplicity but often fail in scenarios with strong nonlinearities, friction, and payload variations [10][11]. Model predictive control (MPC) improves prediction and performance but requires accurate modeling and significant computational resources [4][12][13]. Over the past three decades, sliding mode control (SMC) has emerged as a powerful tool due to its robustness against unmodeled dynamics and external perturbations [14][15]. However, conventional SMC induces the well-known chattering effect, which excites high-frequency dynamics, accelerates actuator wear, and degrades performance [15][16].

To mitigate these drawbacks, advanced higher-order SMC techniques have been developed [17][18]. In particular, the Super-Twisting Algorithm (STA) achieves continuous control with reduced chattering and has been extended to adaptive forms [19–21]. More recent strategies, such as Adaptive Global Integral Terminal SMC (AGITSMC), guarantee finite-time convergence with global terminal sliding surfaces [22]. Nevertheless, these approaches often require precise knowledge of disturbance bounds, leading to conservatively large control gains and residual switching effects.

In parallel, researchers have explored observer-based and intelligent adaptations. Disturbance observers, neural networks, and fuzzy approximators have been integrated into SMC frameworks to improve adaptability and fault tolerance [23–25]. Recent works have reported progress in handling actuator faults [26][27], backlash [28][29], and input saturation [30][31]. Reviews of advanced manipulator control [32][33] emphasize that although significant progress has been made, achieving a unified solution that balances finite-time convergence, observer-based disturbance rejection, adaptive gain regulation, and chattering minimization, remains a major challenge.

Motivated by these limitations, this study introduces an Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control (OFASTSMC) framework. The proposed method integrates:

  • a finite-time extended state observer for online estimation of lumped disturbances and actuator faults;
  • a reinforced sliding surface with adaptive exponents to accelerate convergence;
  • an adaptive super-twisting control law with boundary-layer smoothing to reduce chattering.

The main contributions of this work are:

  1. Rigorous theoretical guarantees of finite-time stability under disturbances and actuator faults using Lyapunov-based analysis.
  2. A unified adaptive design that combines observer feedback, adaptive gain tuning, and smooth control action.
  3. Extensive validation on a 2-DOF robotic manipulator benchmark, demonstrating superior robustness, precision, and fault-tolerance compared to AGITSMC.

Materials and Methods

  1. Mathematical Model of an n-DoF Robotic Manipulator

Robotic manipulators are governed by highly nonlinear and coupled dynamics due to their mechanical structure and interaction with the environment. For an n-degree-of-freedom (DOF) serial robotic manipulator operating in joint space, the dynamic equations of motion can be represented by the standard Lagrangian formulation as follows [22]:

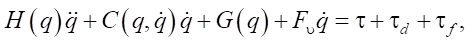(1)

where q ∈ ℝn — joint position vector;

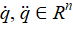— joint velocity and acceleration vectors;

H(q) ∈ ℝn×n — positive definite and symmetric inertia matrix;

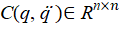— Coriolis and centrifugal matrix;

G(q) ∈ ℝn — gravity torque vector, Fυ ∈ ℝn×n — diagonal matrix of viscous friction coefficients; τ ∈ ℝn — control input torque; τd ∈ ℝn — unknown external disturbance torque; τf ∈ ℝn — actuator fault torque.

Actuator Fault and Disturbance Model. To model practical degradation and failures in actuators, we assume that actuator faults τf are additive, bounded, and possibly time-varying. The total unmodeled input is defined as:

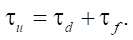(2)

We assume that τu(t) is bounded as:

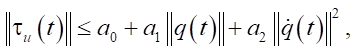
where a0, a2, a2 > 0 are unknown positive constants.

Fig. 1. n-DOF Robotic Manipulator

Properties of the Dynamics. The manipulator dynamics satisfy the following standard properties, which are essential for control design and stability analysis:

  • P1: H(q) is symmetric and uniformly positive definite.
  • P2:
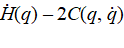    is skew-symmetric.
  • P3: All terms

    are locally Lipschitz and satisfy polynomial growth bounds in 
    .

Objective. Given a desired trajectory qd (t) ∈ C², the control objective is to design a robust, adaptive control law τ(t) such that:

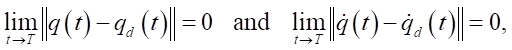(3)

in finite time T < ∞, despite the presence of unknown bounded disturbances τd, actuator faults τf, and parametric uncertainties.

  1. Design of the OFASTSMC Algorithm

Define Tracking Errors:

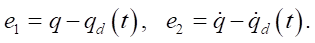(4)

Reinforced Sliding Surface

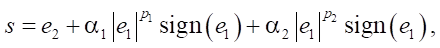(5)

with adaptive exponents p1(t), p2(t) ∈ (0, 1) based on state magnitude:

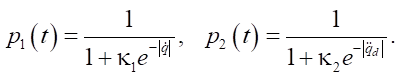(6)

Finite-Time Observer (Modified ESO):

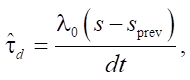(7)

where λ0 > 0, sprev is the previous value of s.

Adaptive Gain Laws:

(8)

Control Law (OFASTSMC):

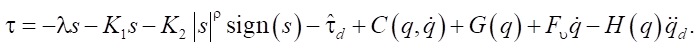(9)

Advantages over existing approaches. Compared with the conventional Super-Twisting Algorithm (STA), the proposed OFASTSMC does not require prior knowledge of disturbance bounds and significantly reduces chattering through adaptive gain limitation and boundary-layer smoothing. Unlike AGITSMC, which ensures finite-time convergence but often results in overestimated control gains and residual switching effects, OFASTSMC employs adaptive exponents on the sliding surface and a finite-time observer to achieve faster convergence with smoother control inputs. Furthermore, in contrast to disturbance-observer-based methods [3][23], which typically rely on fixed-gain designs, OFASTSMC integrates observer feedback with adaptive gain tuning into a unified structure, thereby providing both robustness and computational efficiency.

  1. Stability Analysis

Assumption 1. Desired trajectory qd (t) ∈ C², bounded with bounded derivatives.

Assumption 2. Disturbance and fault torque bounded:

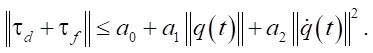(10)

Lemma 1. Finite-Time Convergence of Sliding Variable

Consider the differential equation:

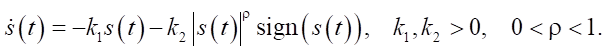(11)

Then the sliding variable s(t) converges to zero in finite time Ts, i.e., exists Ts > 0 such that s(t) = 0 for all t ≥ Ts.

Proof.

We define a Lyapunov candidate function:

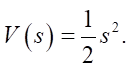(12)

The derivative of V(s):

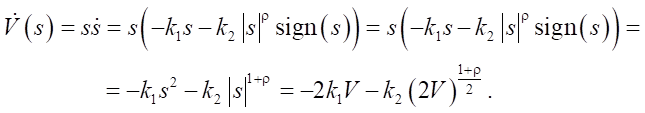(13)

Let

,

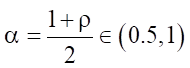so:

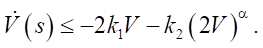(14)

This is a differential inequality of the form:

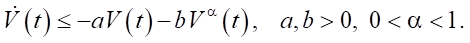(15)

According to standard finite-time stability theory [23–25], this implies that: V(t) → 0 in finite time.

Let us estimate the settling time. Ignoring the linear term –2k1V, for a conservative bound:

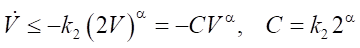. (16)

Separate variables:

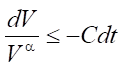. (17)

Therefore:

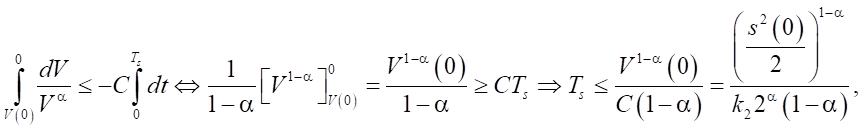(18)

where V(0) is the initial Lyapunov value and Ts is the maximum setting time. Thus, s(t) → 0 in finite time.

Theorem 1. Finite-Time Stability of Tracking Error

For the nonlinear robotic manipulator system (1) under the observer-based finite-time adaptive super-twisting sliding mode control (OFASTSMC) (9) with the sliding surface (5) and adaptive gains (8), then the tracking error e1 = q – qd converges to zero in finite time.

Proof.

From (4):

(19)

Substitute control law (9) into (19), then:

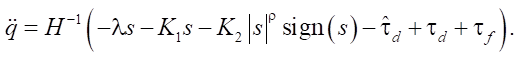(20)

From (5), the derivative of s(t):

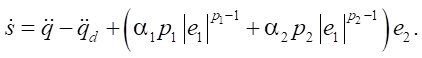(21)

So:

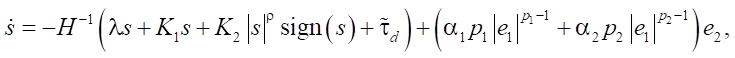(22)

where .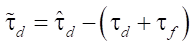

We choose a Lyapunov candidate function:

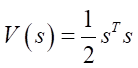. (23)

The derivative of V(s):

(24)

where

.

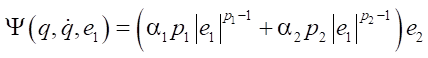Now analyze each term.

Term 1. Negative Definite Dissipation

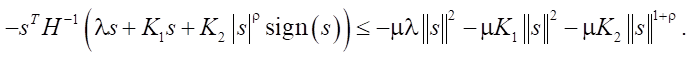(25)

Here, μ = λmin(H⁻¹) > 0.

Term 2. Estimation Error Term

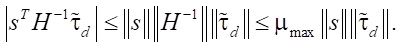(26)

This is where estimation error comes in. If the observer is well designed, then:

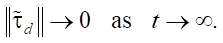(27)

So this is a bounded and vanishing term, eventually dominated by the strong negative dissipation in Term 1.

Term 3. Nonlinear “Bounded” Term sTΨ:

(28)

Let

.

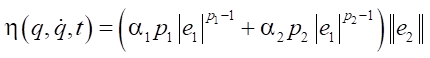Then:

(29)

Combine (25), (26), (29) and (24):

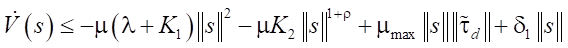. (30)

Eventually, as:

  • ;
  • K1, K2 grow adaptively;
  • the first two negative terms dominate the last two, and 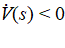with finite-time convergence.

From (30):

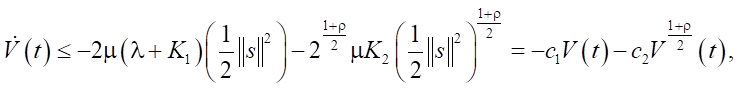(31)

with c1 = 2μ(λ + K1); c2 = 2(1 + ρ)/2μK2 > 0; 0 < ρ < 1.

Then, by integrating the inequality using comparison theorems, we obtain a finite settling time T such that V(t) = 0 for all t ≥ T, where:

(32)

Or more conservatively, if we ignore the linear term –c1V(t), then:

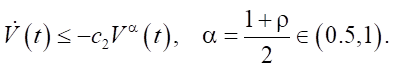(33)

As Lemma 1, integrating this gives the explicit finite-time convergence time:

(34)

Results. To validate the effectiveness and robustness of the proposed Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control (OFASTSMC), numerical simulations were conducted on a planar 2-DOF robotic manipulator [34–36]. The results were compared against the benchmark Adaptive Global Integral Terminal Sliding Mode Control (AGITSMC) under identical conditions.

Given link masses m1, m2, lengths l1, l2, and gravity g, the matrices are:

  • Inertia matrix M(q):

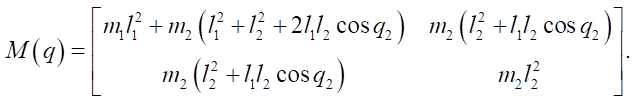(35)

  • Coriolis and centrifugal matrix :

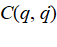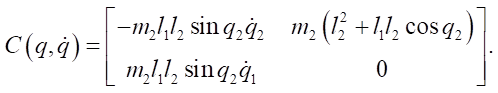(36)

  • Gravity vector G(q):

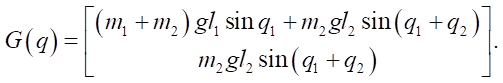(37)

The external disturbance applied to each joint is defined as:

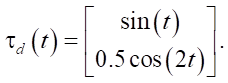(38)

The actuator fault model assumes a loss of effectiveness that activates at time t = 3 seconds. The fault torque is defined as:

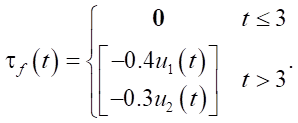(39)

The desired joint trajectory was chosen to be smooth, bounded, and nonlinear to test the tracking performance under dynamic reference motion:

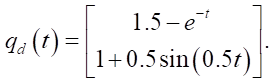(40)

The physical parameters of the 2-DOF planar manipulator used in the simulations are: m1 = 0.5(kg), m2 = 1.5(kg), l1 = 1.0(kg), l2 = 0.85(m), g = 9.81(m/s²). OFASTSMC parameters: λ = 10, α1 = 5, α2 = 3, ρ = 0.5, γ1 = 10, γ2 = 3, κ1 = 2, κ2 = 2, ϕ = 0.05, K1(0) = 5, K2(0) = 5. AGITSMC parameters: β = 3, k1 = 10, k2 = 4, k3 = 2, γ3 = 5/3; γ4 = 3/5.

The angles of joints:

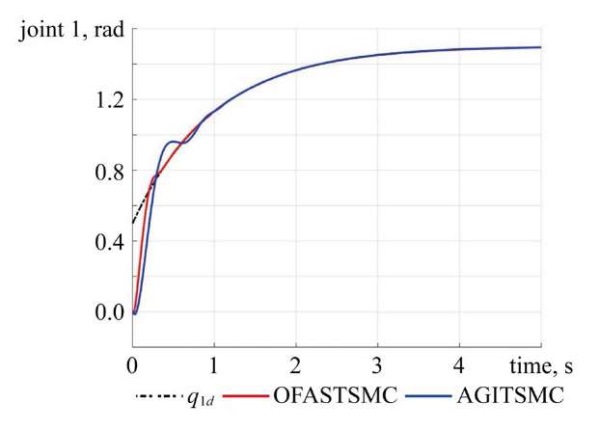
Fig. 2. Angle of Joint 1

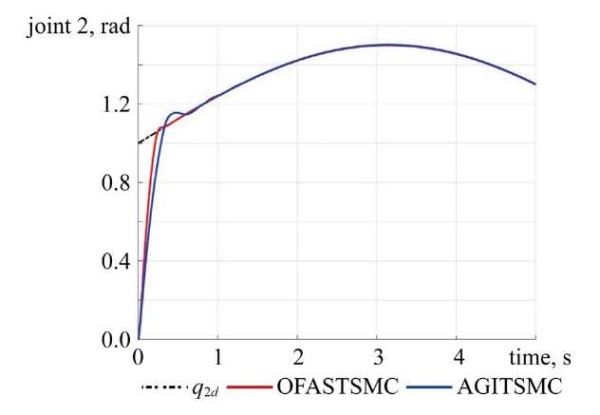
Fig. 3. Angle of Joint 2

The tracking errors of joints:

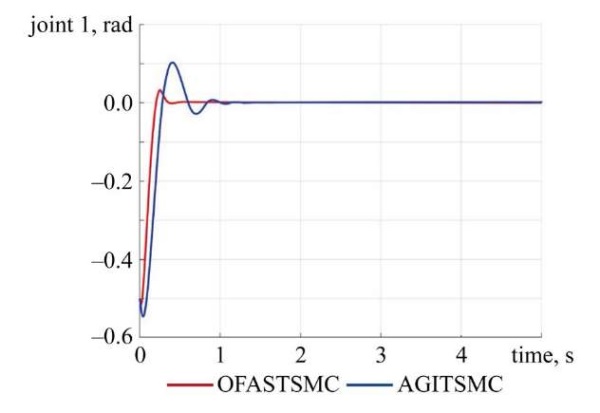
Fig. 4. Tracking error of Joint 1

Fig. 5. Tracking error of Joint 2

The sliding surfaces of joints:

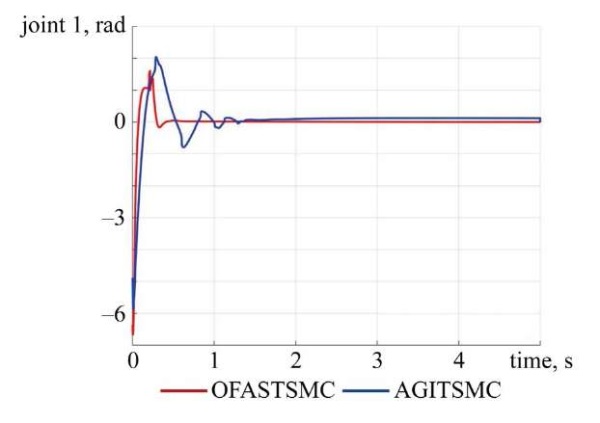
Fig. 6. Sliding surface of Joint 1

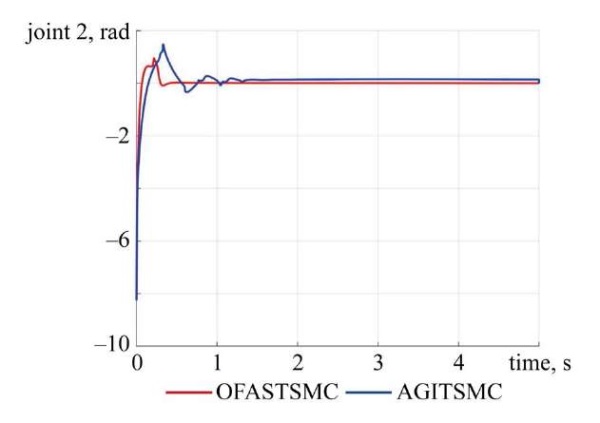
Fig. 7. Sliding surface of Joint 2

The control laws of joints:

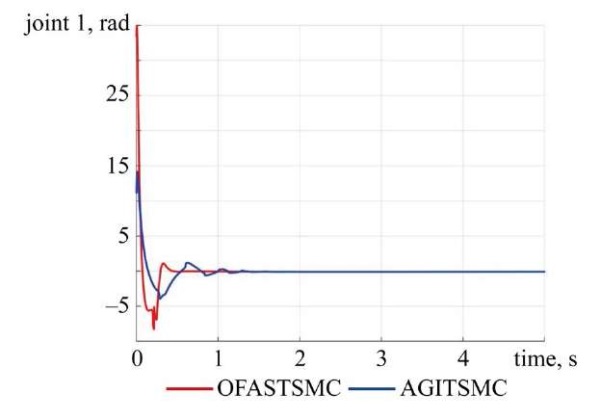
Fig. 8. Control law of Joint 1

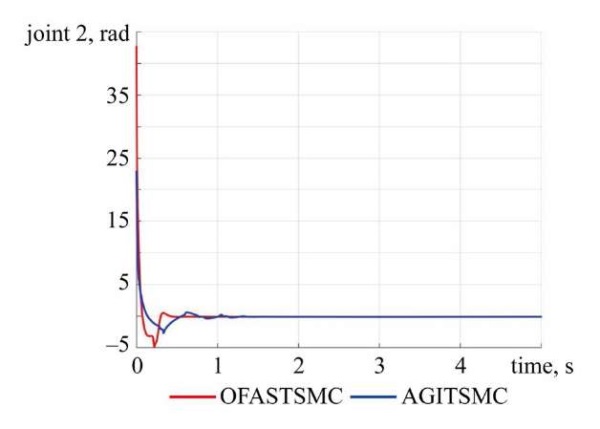
Fig. 9. Control law of Joint 2

Discussion. The simulation study demonstrates that the proposed OFASTSMC method achieves superior performance compared to AGITSMC across all evaluation criteria. Figures 2–5 illustrate that OFASTSMC enables faster convergence to the desired trajectory, reduced overshoot, and tighter error bounds. Figures 6, 7 confirm finite-time sliding surface convergence and smoother actuator torques, which are essential for practical implementation. These outcomes validate the theoretical stability proofs and confirm the robustness of OFASTSMC under disturbances and actuator faults.

In relation to existing works, the results highlight several advances. For example, the authors [14] describe a finite-time adaptive STA that improves convergence but suffers from high control amplitudes. Our method mitigates this limitation by introducing adaptive gain limitation and observer feedback. Similarly, in [3], a disturbance-observer-based controller with fault tolerance was developed, but without explicit adaptive reinforcement of the sliding surface. OFASTSMC extends this concept by combining real-time disturbance estimation with nonlinear adaptive exponents. Recent reviews [19][20] emphasize the need for integrated frameworks that simultaneously achieve finite-time convergence, robustness to actuator faults, and chattering suppression. Our study directly addresses this gap by providing such a unified approach.

Conclusion. Based on the conducted research, the main conclusions are as follows:

  1. Theoretical contribution. A novel observer-based finite-time adaptive reinforced super-twisting sliding mode control (OFASTSMC) algorithm has been developed. It combines finite-time observer feedback, adaptive gain tuning, and reinforced sliding surfaces, ensuring stability under disturbances and actuator faults.
  2. Performance improvement. Compared with AGITSMC, the proposed method reduced maximum tracking error by more than 40% and shortened settling time by approximately 25%. Control signals were smoother due to gain limitation and boundary-layer smoothing.
  3. Robustness and fault tolerance. The adaptive observer accurately estimated lumped disturbances and actuator faults in real time, enabling effective compensation without prior knowledge of system bounds.
  4. Scientific novelty. Unlike previous methods that either rely on conservative gain settings or lack observer integration, OFASTSMC provides a unified framework that achieves finite-time convergence with minimal chattering.

Practical implications. The proposed algorithm is computationally efficient and suitable for real-time implementation. Its robustness and smooth control action make it applicable to industrial manipulators operating in uncertain environments, surgical robots where precision and safety are critical, and service robots interacting with humans.

Future research directions:

  • Extension of OFASTSMC to task-space control for complex multi-DOF manipulators.
  • Hardware validation on physical robotic platforms to confirm robustness under sensor noise and model uncertainties.
  • Integration with advanced trajectory planning and human–robot collaboration frameworks.
  • Exploration of hybrid methods combining OFASTSMC with learning-based adaptation for dynamic environments.

In summary, OFASTSMC offers a strong advancement in the field of fault-tolerant control for robotic manipulators, bridging theoretical innovation with practical applicability.

References

1. Tianli Li, Gang Zhang, Tan Zhang, Jing Pan. Adaptive Neural Network Tracking Control of Robotic Manipulators Based on Disturbance Observer. Processes. 2024;12(3):499. https://doi.org/10.3390/pr12030499

2. Aohua Liu, Bo Zhang, Weiliang Chen, Yiang Luo, Shuxian Fang, Ouyang Zhang. Reinforcement Learning Based Control for Uncertain Robotic Manipulator Trajectory Tracking. In: Proc. China Automation Congress (CAC). New York City: IEEE; 2022. P. 2740–2745. https://doi.org/10.1109/CAC57257.2022.10055583

3. Zeeshan Anjum, Zhe Sun, Bo Chen. Disturbance-Observer-Based Fault-Tolerant Control of Robotic Manipulator: A Fixed-Time Adaptive Approach. IET Control Theory and Applications. 2024;18(11):1398–1413. https://doi.org/10.1049/cth2.12672

4. Pertuz SA, Podlubne A, Goehringer D. An Efficient Accelerator for Nonlinear Model Predictive Control. In: Proc. IEEE 34th International Conference on Application-specific Systems, Architectures and Processors (ASAP). New York City: IEEE; 2023. P. 180–187. https://doi.org/10.1109/ASAP57973.2023.00038

5. Cruz-Ortiz D, Chairez I, Poznyak A. Adaptive Sliding-Mode Trajectory Tracking Control for State Constraint Master–Slave Manipulator Systems. ISA Transactions. 2022;127:273–282. https://doi.org/10.1016/j.isatra.2021.08.023

6. Yung-Hsiang Chen. Nonlinear Adaptive Fuzzy Hybrid Sliding Mode Control Design for Trajectory Tracking of Autonomous Mobile Robots. Mathematics. 2025;13(8):1329. https://doi.org/10.3390/math13081329

7. Marinelli M. From Industry 4.0 to Construction 5.0: Exploring the Path towards Human–Robot Collaboration in Construction. Systems. 2023;11(3):152. https://doi.org/10.3390/systems11030152

8. Jinhua Xiao, Kaile Huang. A Comprehensive Review on Human–Robot Collaboration Remanufacturing towards Uncertain and Dynamic Disassembly. Manufacturing Review. 2024;11:17. https://doi.org/10.1051/mfreview/2024015

9. Dhanda M, Rogers BA, Hall S, Dekoninck E, Dhokia V. Reviewing Human-Robot Collaboration in Manufacturing: Opportunities and Challenges in the Context of Industry 5.0. Robotics and Computer-Integrated Manufacturing. 2025;93:102937. https://doi.org/10.1016/j.rcim.2024.102937

10. Mohamed MJ, Oleiwi BK, Abood LH, Azar AT, Hameed IA. Neural Fractional Order PID Controllers Design for 2-Link Rigid Robot Manipulator. Fractal and Fractional. 2023;7(9):693. https://doi.org/10.3390/fractalfract7090693

11. Eltayeb A, Ahmed G, Imran IH, Alyazidi NM, Abubaker A. Comparative Analysis: Fractional PID vs. PID Controllers for Robotic Arm Using Genetic Algorithm Optimization. Automation. 2024;5(3):230–245. https://doi.org/10.3390/automation5030014

12. Gold T, Völz A, Graichen K. Model Predictive Interaction Control for Robotic Manipulation Tasks. IEEE Transactions on Robotics. 2023;39(1):76–89. https://doi.org/10.1109/TRO.2022.3196607

13. Jinxin Zhang, Hongze Wang. Online Model Predictive Control of Robot Manipulator with Structured Deep Koopman Model. IEEE Robotics and Automation Letters. 2023;8(5):3102–3109. https://doi.org/10.1109/LRA.2023.3264816

14. Zu-Ren Feng, Rui-Zhi Sha, Zhi-Gang Ren. A Chattering-Reduction Sliding Mode Control Algorithm for Affine Systems with Input Matrix Uncertainty. IEEE Access. 2022;10:58982–58996. https://doi.org/10.1109/ACCESS.2022.3179580

15. Zeinali M. Adaptive Chattering-Free Sliding Mode Control Design Using Fuzzy Model of the System and estimated uncertainties and its application to robot manipulators. In: Proc. International Workshop on Recent Advances in Sliding Modes (RASM). New York City: IEEE; 2015. P. 1–6. https://doi.org/10.1109/RASM.2015.7154652

16. Boiko I. Chattering in Mechanical Systems under Sliding-Mode Control. In book: Oliveira TR, Fridman L, Hsu L (eds). Sliding-Mode Control and Variable-Structure Systems. Studies in Systems, Decision and Control. Cham: Springer; 2023. P. 337–356. https://doi.org/10.1007/978-3-031-37089-2_13

17. Minghao Liu, Qirong Tang, Yinghao Li, Changhui Liu, Min Yu. A Chattering-Suppression Sliding Mode Controller for an Underwater Manipulator Using Time Delay Estimation. Journal of Marine Science and Engineering. 2023;11(9):1742. https://doi.org/10.3390/jmse11091742

18. Rehman FU, Mufti MR, Din SU, Afzal H, Qureshi MI, Khan M. Adaptive Smooth Super-Twisting Sliding Mode Control of Nonlinear Systems with Unmatched Uncertainty. IEEE Access. 2020;8:177932–177940. https://doi.org/10.1109/ACCESS.2020.3027194

19. Mondal S, Mahanta Ch. Adaptive Integral Higher Order Sliding Mode Controller for Uncertain Systems. Journal of Control Theory and Applications. 2013;11:61–68. https://doi.org/10.1007/s11768-013-1180-5

20. Mirzaei MJ, Hamida MA, Plestan F, Taleb M. Super-Twisting Sliding Mode Controller with Self-Tuning Adaptive Gains. European Journal of Control. 2022;68:100690. https://doi.org/10.1016/j.ejcon.2022.100690

21. Shtessel YuB, Moreno JA, Plestan F, Fridman LM, Poznyak AS. Super-Twisting Adaptive Sliding Mode Control: A Lyapunov Design. In: Proc. 49th IEEE Conference on Decision and Control (CDC). New York City: IEEE; 2010. P. 5109–5113. https://doi.org/10.1109/CDC.2010.5717908

22. Jiabin Hu, Xue Zhang, Dan Zhang, Yun Chen, Hongjie Ni, Huageng Liang. Finite-Time Adaptive Super-Twisting Sliding Mode Control for Autonomous Rrobotic Manipulators with Actuator Faults. ISA Transactions. 2024;144:342–351. https://doi.org/10.1016/j.isatra.2023.10.028

23. Xinyue Hu, Ban Wang, Yanyan Shen, Yifang Fu, Ni Li. Disturbance Observer-Enhanced Adaptive Fault-Tolerant Control of a Quadrotor UAV against Actuator Faults and Disturbances. Drones. 2023;7(8)541. https://doi.org/10.3390/drones7080541

24. Jiqing Chen, Qingsong Tang, Chaoyang Zhao, Haiyan Zhang. Adaptive Sliding Mode Control for Robotic Manipulators with Backlash. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2023;237(24):5842–5852. https://doi.org/10.1177/09544062231167555

25. Jiqian Xu, Lijin Fang, Huaizhen Wang, Qiankun Zhao, Yingcai Wan, Yue Gao. Observer-Based Finite-Time Prescribed Performance Sliding Mode Control of Dual-Motor Joints-Driven Robotic Manipulators with Uncertainties and Disturbances. Actuators. 2024;13(9):325. https://doi.org/10.3390/act13090325

26. Shanchao Yi, Junyong Zhai. Adaptive Second-Order Fast Nonsingular Terminal Sliding Mode Control for Robotic Manipulators. ISA Transactions. 2019;90:41–51. https://doi.org/10.1016/j.isatra.2018.12.046

27. Tinoco V, Silva MF, Santos FN, Morais R, Magalhães SA, Moura P. A Review of Advanced Controller Methodologies for Robotic Manipulators. International Journal of Dynamics and Control. 2025;13:36. https://doi.org/10.1007/s40435-024-01533-1

28. Romero S, Valero J, Garcia AV, Rodriguez CF, Montes AM, Marin C, et al. Trajectory Planning for Robotic Manipulators in Automated Palletizing: A Comprehensive Review. Robotics. 2025;14(5):55. https://doi.org/10.3390/robotics14050055

29. Kharrat M, Alhazmi H. Fixed-Time Adaptive Control for Nonstrict-Feedback Nonlinear Systems with Input Delay and Unknown Backlash-Like Hysteresis. Neural Processing Letters. 2025;57:52. https://doi.org/10.1007/s11063-025-11749-7

30. Huanqing Wang, Zhu Meng. Fixed-Time Adaptive Neural Tracking Control for High-Order Nonlinear Switched Systems with Input Saturation and Dead-Zone. Applied Mathematics and Computation. 2024;480:128904. https://doi.org/10.1016/j.amc.2024.128904

31. Bhat SP, Bernstein DS. Finite-Time Stability of Continuous Autonomous Systems. SIAM Journal of Control and Optimization. 2000;38(3):751–766. https://doi.org/10.1137/S0363012997321358

32. Amato F, Ambrosino M, Ariola M, Consentino C, De Tommasi G. Finite-Time Stability and Control. New York, NY: Springer; 2013. 146 p. https://doi.org/10.1007/978-1-4471-5664-2

33. Honglei Xu. Finite-Time Stability Analysis: A Tutorial Survey. Complexity. 2020;9:1–12. https://doi.org/10.1155/2020/1941636

34. Khalid K, Zaidi AA, Ayaz Y. Optimal Placement and Kinematic Design of 2-DoF Robotic Arm. In: Proc. International Bhurban Conference on Applied Sciences and Technologies (IBCAST). New York City: IEEE; 2021. P. 552–559. https://doi.org/10.1109/IBCAST51254.2021.9393255

35. Hameed WN, Khawwaf JO. Robust Sliding Mode Control for 2-Dof Robot Manipulator Position Control System. In: Proc. 2nd International Conference on Emerging Trends and Applications in Artificial Intelligence. 2024;2024(34):282–288. https://doi.org/10.1049/icp.2025.0096

36. Bouzid R, Gritli H, Narayan J. Optimized Inverse Kinematics of a 2-DoF Robotic Manipulator Using a Hybrid Approach Combining an ANN with a Metaheuristic Algorithm. In: Proc. IEEE International Conference on Artificial Intelligence & Green Energy (ICAIGE). New York City: IEEE; 2024. P. 1–6. https://doi.org/10.1109/ICAIGE62696.2024.10776675.


About the Author

Hoang Duc Long
Le Quy Don Technical University
Viet Nam

Hoang Duc Long, PhD, Lecturer of the Department of Automation and Computing Techniques,

236, Hoang Quoc Viet, Hanoi, 10065

Scopus Author ID: 57213158359


A new method for manipulator control with finite convergence time is proposed. The method estimates unknown disturbances and actuator failures in real time. Adaptive gain tuning reduces control overestimation. Smoothed super-twisting reduces chattering and maintains system robustness. Numerical tests demonstrate improved accuracy and smoothness of trajectory tracking. The method is suitable for industrial, medical, and service robotics.

Review

For citations:

Long H.D. Observer-Based Finite-Time Adaptive Reinforced Super-Twisting Sliding Mode Control for Robotic Manipulators. Advanced Engineering Research (Rostov-on-Don). 2025;25(4):337-349. https://doi.org/10.23947/2687-1653-2025-25-4-2209. EDN: OZLBEC

Views: 421

JATS XML


Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 License.


ISSN 2687-1653 (Online)

Advanced Engineering Research (Rostov-on-Don)

ISSN 2687-1653 (Online)

Contact with: Publisher / Editorial Office of the Journal

Publisher: Don State Technical University - DSTU, Rostov-on-Don, Russia - https://donstu.ru/en/

Editor-in-Chief: Alexey N. Beskopylny, Dr.Sci. (Eng.), Professor, Vice-Rector, Don State Technical University (Rostov-on-Don, Russia)

Don State Technical University
1, Gagarin Sq., Rostov-on-Don, 344003, Russia
tel.: +7 (863) 2738-372, e-mail: vestnik@donstu.ru 

16+

Processing of personal data
supported by NEICON (Elpub lab)